which of the following is an equivalent expression for 8 ^ 3 * 6 ^ 3?48 ^ 3, 14 ^ 6, 48 ^ 6, 14 ^ 3
Answers
We want to know an equivalent expression for:
\(8^3\cdot6^3\)We remember the property power of a product, which says:
\((a\cdot b)^n=a^n\cdot b^n\)And thus, using it we obtain:
\(8^{3^{}}\cdot6^3=(8\cdot6)^3=48^3\)This means that an equivalent expression is 48³.
Related Questions
you have to find ABC and I'm not sure how to any help is appreciated

Answers
Hello,
Since (BD) bissects angle ABC,
18-x=26-3x
2x=8
x=4
18-x=18-4=14
m angle ABC=14°*2=28°
Please help what is the slope of the line?
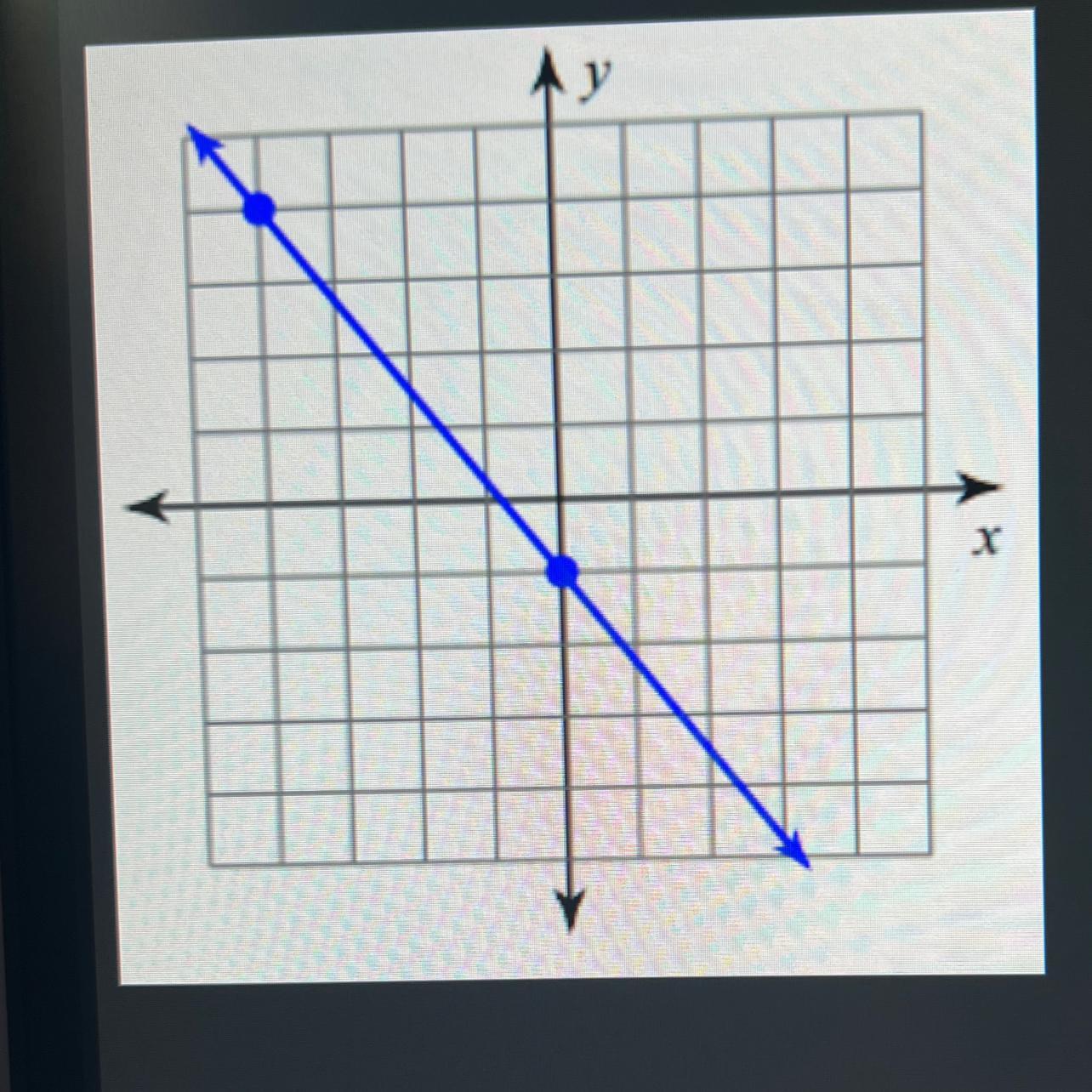
Answers
Answer:
-5/4
Step-by-step explanation:
Let \((x_1,y_1)=(-4,4)\) and \((x_2,y_2)=(0,-1)\). The slope of the line would be:
\(\displaystyle \frac{y_2-y_1}{x_2-x_1}=\frac{-1-4}{0-(-4)}=\frac{-5}{4}=-\frac{5}{4}\)
Answer: -5/4
Step-by-step explanation:
To find the slope between two points, you can use the formula:
Slope = (y2 - y1)/(x2 - x1)
Using the points (0, -1) and (-4, 4), we can substitute the coordinates into the formula:
slope = (4 - (-1))/(-4 - 0)
slope = (4 + 1)/(-4)
slope = 5/-4
Therefore, the slope between the two points is -5/4.
Complete the table of values for the equation 4x + 2y =64
Answers
The completed table of values for the equation 4x + 2y = 64 is provided .
To complete the table of values for the equation 4x + 2y = 64, we can assign different values to x and solve for y. Let's choose a range of values for x and calculate the corresponding values of y.
Table of Values:
x y
0 32
4 28
8 24
12 20
16 16
20 12
24 8
28 4
32 0
To find the values of y, we substitute each x-value into the equation and solve for y. For example, when x is 0, we have 4(0) + 2y = 64, which simplifies to 2y = 64 and y = 32. Similarly, for x = 4, we have \(4(4) + 2y = 64\), which simplifies to \(16 + 2y = 64\) and\(y = 28.\)
By continuing this process for the remaining values of x, we can complete the table of values for the equation 4\(x + 2y = 64.\)
For more questions on equation
https://brainly.com/question/29174899
#SPJ8
Which equation is equivalent to 10=3/2(2x+4)?
a.10=3x+2
b.10=3x+4
c.10=3x+6
d.10=3x+12
Answers
Answer
the answer should be C. 10=3x+6
Help please question in the picture
Answers
Answer:
lol no picture attach it please
Step-by-step explanation:
-x < - 29 solve for x
Answers
Answer:
x<29
Step-by-step explanation:
divide both sides by -1 since x cannot be negative
Solve:
-14 + (-3) =
O 11
0 -17
O 17
0-11

Answers
Answer:
-17 ...............................
What are the coordinates of the vertices of the image triangle after a 90 clockwise rotation about the origin? :
A'(1, 3) B'(-3, 4) C'(-2,-3)
A'(3, 1) B'(4,-3) C'(-3,-2)
A'(3,-1) B'(4, 3) C'(-3, 2)
A'(1,-3) B'(-3,-4) C'(-2, 3)
A'(-3, 1) B'(-4,-3) C'(3,-2)
Answers
Before carrying out rotation transformation, the coordinates of the vertices of the pre-image are;
A (3, -6)
B(1, 2)
C (7, -1).
What is the effect of clockwise rotation transformation?We are given the coordinates of the transformed image as:
A'(6, 3),
B'(–2, 1),
C'(1, 7).
We need to find the coordinates of the pre-image A, B and C.
The rule for rotation of 90° about the origin is (x,y) ---> (-y,x).
But we need to find the coordinates of the vertices of the pre-image.
So, we need to apply rule (-y,x) ---->(x,y).
Applying the 90 degrees clockwise rotation rule,
A'(6, 3) -----> A (3, -6)
B'(–2, 1) -----> B(1, 2)
C'(1,7) -----> C (7, -1).
Therefore, coordinates of the vertices of the pre-image are
A (3, -6)
B(1, 2)
C (7, -1).
Read more about clockwise rotation transformation at; https://brainly.com/question/26249005
#SPJ1
Complete question is;
After a rotation of 90° about the origin, the coordinates of the vertices of the image of a triangle are A'(6, 3), B'(–2, 1), and C'(1, 7). What are the coordinates of the vertices of the pre-image?
Right triangle EFG has its right angle at F, EG = 6 , and FG = 4 What is the value of the trigonometric ratio of an angle of the triangle? Drag a value to each box to match the trigonometric ratio with its value .

Answers
Answer:
\(\cos G=\dfrac{2}{3}\)
\(\csc E=\dfrac{3}{2}\)
\(\cot G=\dfrac{2}{\sqrt{5}}\)
Step-by-step explanation:
If the right angle of right triangle EFG is ∠F, then EG is the hypotenuse, and EF and FG are the legs of the triangle. (Refer to attached diagram).
Given ΔEFG is a right triangle, and EG = 6 and FG = 4, we can use Pythagoras Theorem to calculate the length of EF.
\(\begin{aligned}EF^2+FG^2&=EG^2\\EF^2+4^2&=6^2\\EF^2+16&=36\\EF^2&=20\\\sqrt{EF^2}&=\sqrt{20}\\EF&=2\sqrt{5}\end{aligned}\)
Therefore:
EF = 2√5FG = 4EG = 6\(\hrulefill\)
To find cos G, use the cosine trigonometric ratio:
\(\boxed{\begin{minipage}{9 cm}\underline{Cosine trigonometric ratio} \\\\$\sf \cos(\theta)=\dfrac{A}{H}$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}\)
For angle G, the adjacent side is FG and the hypotenuse is EG.
Therefore:
\(\cos G=\dfrac{FG}{EG}=\dfrac{4}{6}=\dfrac{2}{3}\)
\(\hrulefill\)
To find csc E, use the cosecant trigonometric ratio:
\(\boxed{\begin{minipage}{9 cm}\underline{Cosecant trigonometric ratio} \\\\$\sf \csc(\theta)=\dfrac{H}{O}$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}\)
For angle E, the hypotenuse is EG and the opposite side is FG.
Therefore:
\(\csc E=\dfrac{EG}{FG}=\dfrac{6}{4}=\dfrac{3}{2}\)
\(\hrulefill\)
To find cot G, use the cotangent trigonometric ratio:
\(\boxed{\begin{minipage}{9 cm}\underline{Cotangent trigonometric ratio} \\\\$\sf \cot(\theta)=\dfrac{A}{O}$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}\)
For angle G, the adjacent side is FG and the opposite side is EF.
Therefore:
\(\cot G=\dfrac{FG}{EF}=\dfrac{4}{2\sqrt{5}}=\dfrac{2}{\sqrt{5}}\)

Find the mean, median, mode 1. 40, 38,29,34,37, 22, 15, 38 2. 26, 32, 12, 18, 11, 14, 21, 12,27 3. 3,3,4,7,5,7,6,7,8,8,8. 9,8, 10, 12, 9, 15, 15
NEED THE ANSWER ASAP
NONSENSE, REPORT
i will (brainliest) if it's correct!!!

Answers
Mean: 34.125, Median: 31.5, Mode: 38
Mean: 19.222, Median: 18, No mode
Mean: 8.611, Median: 8, Mode: 8
Let's find the mean, median, and mode for each set of numbers:
Set: 40, 38, 29, 34, 37, 22, 15, 38
Mean: To find the mean, we sum up all the numbers and divide by the total count:
Mean = (40 + 38 + 29 + 34 + 37 + 22 + 15 + 38) / 8 = 273 / 8 = 34.125
Median: To find the median, we arrange the numbers in ascending order and find the middle value:
Arranged set: 15, 22, 29, 34, 37, 38, 38, 40
Median = (29 + 34) / 2 = 63 / 2 = 31.5
Mode: The mode is the number(s) that appear(s) most frequently in the set:
Mode = 38 (appears twice)
Set: 26, 32, 12, 18, 11, 14, 21, 12, 27
Mean: Mean = (26 + 32 + 12 + 18 + 11 + 14 + 21 + 12 + 27) / 9 = 173 / 9 ≈ 19.222
Median: Arranged set: 11, 12, 12, 14, 18, 21, 26, 27, 32
Median = 18
Mode: No mode (all numbers appear only once)
Set: 3, 3, 4, 7, 5, 7, 6, 7, 8, 8, 8, 9, 8, 10, 12, 9, 15, 15
Mean: Mean = (3 + 3 + 4 + 7 + 5 + 7 + 6 + 7 + 8 + 8 + 8 + 9 + 8 + 10 + 12 + 9 + 15 + 15) / 18 ≈ 8.611
Median: Arranged set: 3, 3, 4, 5, 6, 7, 7, 7, 8, 8, 8, 8, 9, 9, 10, 12, 15, 15
Median = 8
Mode: Mode = 8 (appears 4 times)
Mean: 34.125, Median: 31.5, Mode: 38
Mean: 19.222, Median: 18, No mode
Mean: 8.611, Median: 8, Mode: 8
For more questions on Mean
https://brainly.com/question/1136789
#sPJ8
keri rented a canoe from a rental company for atotal of $35.00 the company charges $10.50 for the first hour and $8.25 per hour for each additional hour.
Answers
Answer:
She rented it for 3 hours.
8.25 times 3 plus 10.50 = 35.00
1
If a +b = 6 and a= 2, what is b
A(0
B(2
C(4
D(6
Answers
Answer:
C(4
Step-by-step explanation:
a + b = 6
2 + b = 6 plug in
-2 -2 Subtract 2 from both sides
b = 4
Find the midpoint of the segment with the given endpoints.
(-1,1) and (-1,9)
Answers
Answer:
(-1, 5)
Step-by-step explanation:
The midpoint of a line segment is given by the formula:
\(\boxed{\text{Midpoint}=(\frac{x_1+x_2}{2} ,\frac{y_1+y_2}{2} )}\)
Using the formula above,
midpoint of segment
= \((\frac{-1-1}{2},\frac{1+9}{2})\)
= \((\frac{-2}{2},\frac{10}{2})\)
= (-1, 5)
For a similar question on midpoint, check out: https://brainly.com/question/14687140
Shown is a circle, centre C, with diameter AE.
PQ is a tangent to the circle, meeting it at E.
A EDQ is isosceles with ED= EQ.
Given that / EAD = 50°, calculate the size
of Z DQE.

Answers
Answer:
∠DQE = 65°
Step-by-step explanation:
You want to know the measure of Angle DQE in the given figure.
Right triangleTriangle ADE is inscribed in a semicircle, so is a right triangle. That makes acute angle AED complementary to acute angle EAD. The latter is given as 50°, so ...
∠AED = 90° -50° = 40°
TangentWe know that tangent line QE is perpendicular to diameter AE, so angle AEQ is a right angle. Segment ED divides that right angle into complementary angles, so ...
∠DEA +∠DEQ = 90°
∠DEQ = 90° -∠DEA = 90° -40° = 50°
Isosceles triangleA.pex angle DEQ in isosceles triangle DEQ being 50° means that the base angles QDE and DQE will have measure ...
∠DQE = (180° -50°)/2 = 130°/2
∠DQE = 65°
__
Alternate solution
Let angles DQE and QDE be represented by x. Then the sum of angles in quadrilateral ADQE is 360°:
50° +(90+x)° +x° +90° = 360°
230° +2x = 360° . . . . . . simplify
x = 130°/2 = 65° . . . . . solve for x
solve following problem

Answers
Answer:
p²=h²-b²
p² =10²-6²
p² =100-36
p²=64
p=( √8)²
p=8
Let \(x\) and \(y\) be the length and height, respectively, of the rectangle.
Let the bottom left vertex be the origin (0, 0), and position the triangle so that the bottom leg lies on the horizontal axis in the \(x,y\)-plane. The hypotenuse of the triangle then lies on the line through (0, 0) and (6, 8), with slope 8/6 = 4/3. Then for some \(x\) between 0 and 6, we have \(y = \frac43x\).
This means for some fixed distance \(x\) from the origin, the rectangle has length \(6-x\) and height \(\frac43x\). Thus the area of the rectangle can be expressed completely in terms of \(x\) as
\(A(x) = (6-x) \times \dfrac43x = 8x - \dfrac43 x^2\)
Non-calculus method:
Complete the square to get
\(8x - \dfrac43 x^2 = -\dfrac43 (-6x + x^2) = 12 - \dfrac43 (9 - 6x + x^2) = 12 - \dfrac43 (x-3)^2\)
which is maximized when the quadratic term vanishes at \(x=3\), giving a maximum volume of \(\boxed{12\,\mathrm{in}^2}\).
Calculus method:
Differentiate \(A(x)\) and find the critical points.
\(A'(x) = 8 - \dfrac83 x = 0 \implies x = 3\)
Differentiate again to check the sign of the second derivative at the critical point.
\(A''(x) = -\dfrac83 \implies A''(3) = -\dfrac83 < 0\)
which indicates a local maximum at \(x=3\). Hence the maximum area is \(A(3) = 12\), as before.
which expression is equivalent to n+n-0.18n
a. 1.18n
b. 1.82n
c. n- 0.18
d. 2n - 0.82
Answers
Answer:
Simplifying the expression `n + n - 0.18n`, we get:
n + n - 0.18n = 2n - 0.18n
Therefore, the expression `n + n - 0.18n` is equivalent to `2n - 0.18n`.
Looking at the answer choices:
a. 1.18n
b. 1.82n
c. n- 0.18
d. 2n - 0.82
We can see that choice d is equivalent to the simplified expression `2n - 0.18n`.
Therefore, the answer is d. 2n - 0.82.
Step-by-step explanation:
A
-2+
Which graph represents the
function y = tan x?
B
2T
2T
D
-2+1
21
4+
ㅠ
2T
2πT

Answers
The graph that represents the function y= tanx is Option A.
What is the description of the above function?The graph of y =tan (x) is a periodic function that has vertical asymptotes at x = (n + 1/2)π, where n is an integer.
It oscillates between positive and negative infinity, creating a wave- like pattern.
It has a repeating pattern of sharp peaks and valleys, exhibiting both positive and negative slopes.
Thus, option A is the correct answer.
Learn more about graph:
https://brainly.com/question/25184007
#SPJ1

Jack borrowed $1.50 from his friend Jenna every day for five days last week. What rational number represents how much Jack owed his friend last week?
Answers
Answer:
$7.50
Step-by-step explanation:
set up an equation: $ x days = total owed
1.50 x 5 = 7.50
A polling company conducted a survey asking 40 fourth year students from Ohio and 33 fourth-year students from Pennsylvania about on average, how many hours they spend on the computer per week. Ohio had an average of 52, while Pennsylvania had an average of 33. Ohio and Pennsylvania have standard deviations of 7.22 and 10.11 respectively. Construct a 99.9% confidence interval for the difference between these results.
Answers
Answer:
The 99.9% confidence interval for the difference between these results is between 12.09 and 25.91 hours per week.
Step-by-step explanation:
Before building the confidence interval, we need to understand the central limit theorem and subtraction between normal variables.
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean \(\mu = p\) and standard deviation \(s = \sqrt{\frac{p(1-p)}{n}}\)
Subtraction of normal variables:
When two normal variables are subtracted, the mean is the subtraction of the means, while the standard deviation is the square root of the sum of variances.
Ohio had an average of 52, standard deviation of 7.22, sample of 40.
This means that \(\mu_O = 52, s_O = \frac{7.22}{\sqrt{40}} = 1.1416\)
Pennsylvania had an average of 33, standard deviation of 10.11, sample of 33.
This means that \(\mu_P = 33, s_P = \frac{10.11}{\sqrt{33}} = 1.76\)
Distribution of the difference:
\(\mu = \mu_O - \mu_P = 52 - 33 = 19\)
\(s = \sqrt{s_O^2 + s_P^2} = \sqrt{1.1416^2 + 1.76^2} = 2.1\)
Confidence interval:
We have that to find our \(\alpha\) level, that is the subtraction of 1 by the confidence interval divided by 2. So:
\(\alpha = \frac{1 - 0.999}{2} = 0.0005\)
Now, we have to find z in the Ztable as such z has a pvalue of \(1 - \alpha\).
That is z with a pvalue of \(1 - 0.0005 = 0.9995\), so Z = 3.29.
Now, find the margin of error M as such
\(M = zs\)
\(M = 3.29*2.1 = 6.91\)
The lower end of the interval is the sample mean subtracted by M. So it is 19 - 6.91 = 12.09 hours per week
The upper end of the interval is the sample mean added to M. So it is 19 + 6.91 = 25.91 hours per week.
The 99.9% confidence interval for the difference between these results is between 12.09 and 25.91 hours per week.
Find the complete factored form of the
polynomial :
-8m²n-7m² nª
Enter the correct answer.
Answers
The polynomial -8m²n - 7m²n can be factored using the common factor -m²n. The complete factored form of the polynomial is (-m²n) (8 + 7a).
To find the complete factored form of the polynomial -8m²n - 7m²n, we can factor out common terms from both the terms. The common factor in the terms -8m²n and -7m²n is -m²n. We can write the polynomial as:
-8m²n - 7m²n = (-m²n) (8 + 7a)
Therefore, the complete factored form of the polynomial -8m²n - 7m²n is (-m²n) (8 + 7a). This expression represents the original polynomial in a multiplied form. We can expand this expression using distributive law to verify that it is equivalent to the original polynomial.
For more such questions on polynomial, click on:
https://brainly.com/question/1600696
#SPJ8
Refer to the table summarizing service times (seconds) of dinners at a fast food restaurant. How many individuals are included in the summary? Is it possible to identify the exact values of all of the original service times?
Time (sec) Frequency
60 to 119 7
120 to 179 24
180 to 239 14
240 to 299 1
300 to 359 4
Answers
Answer:
Based on the provided information, the table summarizes service times (in seconds) of dinners at a fast food restaurant. To determine the number of individuals included in the summary, we can sum up the frequencies listed in the table:
7 + 24 + 14 + 1 + 4 = 50
Therefore, there are 50 individuals included in the summary.
Regarding the exact values of all the original service times, it is not possible to determine them precisely based on the given information. The table only provides ranges of service times and their corresponding frequencies. We can determine the range within which each individual's service time falls, but we cannot determine the exact value within that range.
can someone pls look at the recent questions on my page.
Answers
Answer:
sure I will
Step-by-step explanation:
please give brainiest
Answer:
where is your pic can you post
Pls help, i will give brainliest:
Consider the graphs which summarize the data on the number of hours per week of television viewing by two groups: 12-17 year-old Girls and 12-17 year-old Boys. Choose all that are correct.
The median for the girls is 16.
The median for the boys is 22.
The interquartile range for the girls is 28
The interquartile range for the boys is 16
The difference between the medians as a multiple of the IQR is 1/4
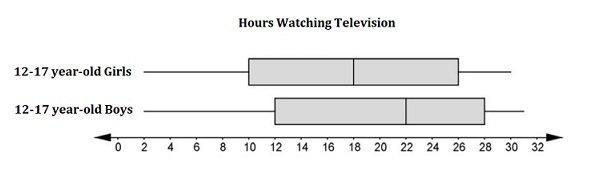
Answers
Answer:
a,b,e
Step-by-step explanation:
Answer:
B, D, E
OR
The median for the boys is 22
The interquartile range for the boys is 16
The difference between the medians as a multiple of the IQR is 1/4
Step-by-step explanation:
I just did it and got it right
If M is the set of all square numbers less than 80 and N is the set of all non-negative even numbers that are under 30, Write the lists of all elements of M and N.

Answers
Answer:
The set M of all square numbers less than 80 is:
M = {0, 1, 4, 9, 16, 25, 36, 49, 64}
The set N of all non-negative even numbers that are under 30 is:
N = {0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28}
Answer:
All elements of the set M in ascending order are:
1, 4, 9, 16, 25, 36, 49, 64All elements of the set N in ascending order are:
0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28Step-by-step explanation:
A square number, also known as a perfect square, is a non-negative integer that is obtained by multiplying an integer by itself. In other words, it is the result of squaring an integer.
The square numbers less than 80 are:
1, 4, 9, 16, 25, 36, 49, and 64.An even number is an integer that is divisible by 2 without leaving a remainder.
The non-negative even numbers that are under 30 are:
0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, and 28.Therefore:
All elements of the set M in ascending order are:
1, 4, 9, 16, 25, 36, 49, 64All elements of the set N in ascending order are:
0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28Heeeeeeeeeeeeeeeellllppp

Answers
Answer:
The Area = 28.26 or 28.27 depends if you round or not
- Suppose y varies directly as x. If y = -7 when x = -14, find y when x=3
Answers
Answer:1.5
Step-by-step explanation:
Y=1/2 of x
What should you substitute for x in the second equation (bottom equation) in order to solve the system by the substitution method?

Answers
We substitute -1+1/6y for x in the second equation (bottom equation) in order to solve the system by the substitution method.
The given system of equations are 2x-1/3y = -2...(1)
3x+y=1...(2)
We solve this system of equations by using substitution method.
Let us solve for x in equation to substitute it in equation (2).
2x=-2+1/3y
Divide both sides of equation by 2.
x=-1+1/6y
Now plug in the value of x in equation 2.
Hence, we substitute -1+1/6y for x in the second equation (bottom equation) in order to solve the system by the substitution method.
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ1
3. An elevator is moving upward with a speed of 14.3 m/s . Two seconds later, the elevator is still moving upward, but its speed bas been reduced to 3.7 m/s . What is the average acceleration of the clevator during the 2.0 interval?
Answers
By definition of average acceleration,
a (average) = (3.7 m/s - 14.3 m/s) / (2.0 s) = -5.3 m/s²
1. 30% of ___ = 90
2. 20% of ___ = 40
Answers
Answer:
1. 300
2. 200
Hope this helps!
Answer:
30% of 300 = 90
20% of 200 = 40
A pyramid is composed of six isosceles triangles and a hexagonal base. Each isosceles triangle has a height of 8 inches and a base of 6 inches. The area of the hexagonal base is 93.5 square inches. What is the surface area of the pyramid? Enter your answer in the box. in²
Answers
The surface area of the pyramid is A = 265.23 inches²
What is the surface area of the pyramid?The total surface area is the summation of the areas of the base and the three other sides. A = B + ( 1/2 ) ( P x h ), where B is the area of the base of the pyramid, P is the perimeter of the base, and h is the slant height of the pyramid
Surface Area of Pyramid = B + ( 1/2 ) ( P x h )
Given data ,
Let the surface area of hexagonal pyramid be represented as A
Surface area of hexagonal pyramid = Area of base + area of lateral surface
Area of the base = 93.5 inches²
Now , the Area of the lateral surface = 3a √ ( h² + ( 3a²/4 ) )
where a = 6 inches
h = 8 inches
Substituting the values in the equation , we get
Area of the lateral surface = ( 3 x 6 ) √ ( 64 + ( 3 x 36 / 4 ) )
On simplifying the equation , we get
Area of the lateral surface = 171.7 inches²
So , Surface area of hexagonal pyramid = Area of base + area of lateral surface
Surface area of hexagonal pyramid A = 93.5 inches² + 171.7 inches²
Surface area of hexagonal pyramid A = 265.23 inches²
Hence , the surface area of hexagonal pyramid is 265.23 inches²
To learn more about surface area of pyramid click :
https://brainly.com/question/15050758
#SPJ1