Which of the following is a point-slope equation of a line that passes through
the points (10,5) and (4, -7)?
A. y-5= 2(x-10)
B. Y-5 = -2(x-10)
C. y-10 = 2(x-5)
D. y-10 = -2(x-5)
Answers
Answer:
A
Step-by-step explanation:
m = Y2 - Y1/ X2 - X1
m= -7 - 5/ 4 - 10
m = -12/ -6
m = 2
y - y1 = m ( x - x1)
y - 5 = 2 (x - 10)
Related Questions
A football team played a total of 25 games. They won 20 draw 3 and lost 2. What fractions of the game did they win
Answers
Answer:
4/5
Step-by-step explanation:
total number of games played = 25
total number of games won = 20
total number of games lost = 2
total number of draw games = 3
the fraction of the games they won = (total number of games won) ÷ (total number of games played)
=20/25
=4/5
A and B are two cities measure the bearing from b to a and a to be
Answers
The bearing of city B from A is 030° and the bearing of city A from B is 210°.
What is bearing angle?The term bearing is used in the navigation. The bearing is the horizontal angle which is made between the direction of an object to the another object.
This angle is measure in the clockwise direction from the north direction.
For example, if 40 clockwise from the north direction is represented as 040° in a bearing angle.
The two cities in the attached image below are show. The city A is at some distance from the city B.
Let suppose the city B is from 30 degrees from the north on clockwise. Thus, to measure of the bearing of B from A will be 030°.
Now add 180 degree to this angle to get the bearing of A from B. Thus,
180°+30°=210°
Hence, the measure of the bearing of city B from A is 030° and measure the bearing of city A from B is 210°.
Learn more about the bearing angle here;
brainly.com/question/23427938.
#SPJ9

When computing a correlation coefficient, if you have the degrees of freedom of 55, your sample size must be:
Answers
Answer: Your sample size must be 57 .
Step-by-step explanation:
The degrees of freedom of a data describes the number of data values that are free to vary.The degrees of freedom(df) require to calculate the correlation coefficient is N-2, where N is the sample size.
If Degrees of freedom(df) is given as 55, then
N-2 =55
Add 2 on both sides , we get
N= 55+2=57
Therefore , the required sample size = 57
the angel of elevation from a ball on a football field to the top of a 30 foot tall goal post 16 degree 42'. How far is the football from the base of the goal post? Round to the nearest tenth of a foot.
Answers
The football is approximately 96.4 feet from the base of the goal post.
What is tangent function?The tangent function in trigonometry is used to determine the proportion between the lengths of the adjacent and opposite sides in a right triangle. Where theta is the angle of interest, the tangent function is defined as:
tan(theta) = opposing / adjacent.
When the lengths of one side and one acute angle are known, the tangent function is used to solve for the unknown lengths or angles in right triangles. In order to utilise the tangent function, we must first determine the angle of interest, name the triangle's adjacent and opposite sides in relation to that angle, and then calculate the ratio of those sides using the tangent function.
Given, the angle of elevation is 16 degrees 42'.
That is,
Angle of elevation = 16 degrees 42' = 16 + 42/60 = 16.7 degrees
Using tangent function we have:
tan(16.7) = 30/x
x = 30 / tan(16.7)
x = 96.4 feet
Hence, the football is approximately 96.4 feet from the base of the goal post.
Learn more about tangent function here:
https://brainly.com/question/22043858
#SPJ1
Find the monthly payment for the loan. Finance $500,000 for an apartment complex with a 12.3% 10-year loan.
Please round the answer to the nearest cent. The monthly payment is ?
Answers
Using it's formula, it is found that the monthly payments for the loan of the apartment is of $7,260.50.
What is the monthly payment formula?It is given by:
\(A = P\frac{\frac{r}{12}\left(1 + \frac{r}{12}\right)^n}{\left(1 + \frac{r}{12}\right)^n - 1}\)
In which:
P is the initial amount.r is the interest rate.n is the number of payments.In this problem, the parameters are given as follows:
P = 500000, r = 0.123, n = 12 x 10 = 120.
Hence:
r/12 = 0.123/12 = 0.01025.
Then, the monthly payments will be of:
\(A = P\frac{\frac{r}{12}\left(1 + \frac{r}{12}\right)^n}{\left(1 + \frac{r}{12}\right)^n - 1}\)
\(A = 500000\frac{0.01025(1+0.01025)^{120}}{(1+0.01025)^{120} - 1}\)
A = 7260.50.
More can be learned about the monthly payment formula at https://brainly.com/question/26267630
#SPJ1
You draw a rectangle with vertices at (-3.5,3), (3.5,3), (3.5,-3), and (-3.5,-3).
What is the perimeter and area of the rectangle?
Answers
The perimeter and the area of the rectangle are 26 units and 42 square units, respectively.
What is a rectangle?A rectangle is a quadrilateral with all four interior angles 90°.
Given that, the vertices of the rectangle are (-3.5,3), (3.5,3), (3.5,-3), and (-3.5,-3).
The length of the rectangle is:
l = 3.5 - (-3.5)
l = 3.5 + 3.5
l = 7
The width of the rectangle is:
w = 3-(-3)
w = 3 + 3
w = 6
The perimeter of the rectangle is given by:
P = 2 (l +w)
P = 2(7 + 6)
P = 26
The area of the rectangle is:
A = l × w
A = 7 × 6
A = 42
Hence, the perimeter and the area of the rectangle are 26 units and 42 square units, respectively.
Learn more on rectangles here:
https://brainly.com/question/15019502
#SPJ1
On 31st August 2018, Musk Traders purchased a machine on credit for a cost price of R402 500 (including VAt at 15 percent). Machinery is depreciated over six years according to the straight line basis and there is no residual value on this machine as it is highly specialised. Musk Traders has a 30 June year-end.
Calculate the depreciation and accumulated depreciation for 2019 and 2020
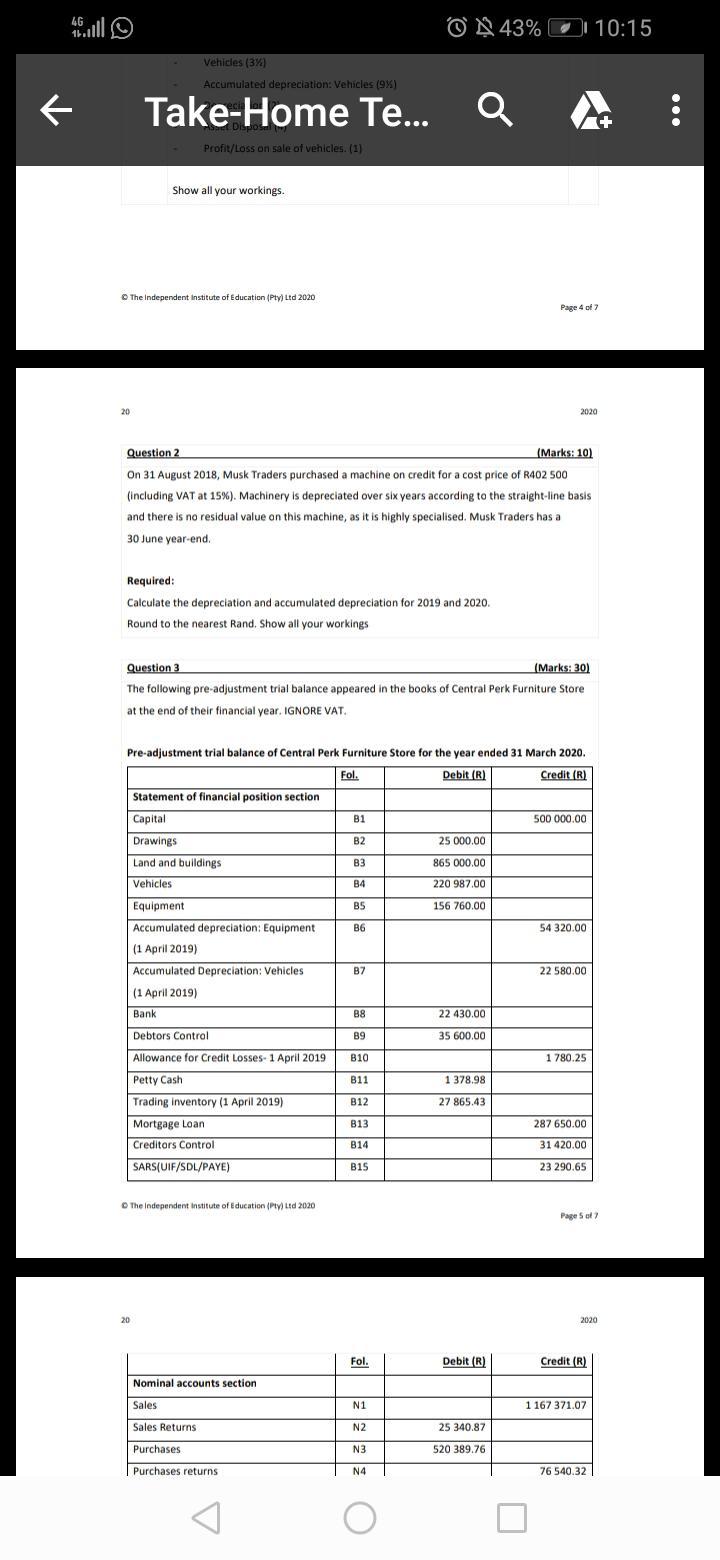
Answers
Answer:
The depreciated asset price has to be independent of VAT;
= 402,500/1.15
= $350,000
Annual Depreciation = 350,000/6 years
= $58,333
Musk Trading has a 30 June year end so;
2019September to June = 10 months
Depreciation;
= 58,333 * 11/12
= $48,611
Accumulated Depreciation = $48,611
2020Depreciation = Annual depreciation of $58,333
Accumulated depreciation
= 2019 depreciation + 2020 depreciation
= 48,611 + 58,333
= $106,944
PLEASE HELP MEEEE! Don’t mind the highlighter haha
Answers
Answer:
c words words words words
Combine the like terms to create an equivalent expression 4p+6-3
Answers
Answer:
-3/4
Step-by-step explanation:
4p+6-3=0
4p+3=0
4p=-3
p= -3/4
The diameter of a bicycle wheel is 60 centimeters. How far does the wheel travel when it makes 35 revolutions? Give your answer in. meters( Math in focus singapore math course 1 B)
Answers
Answer:
The circumference of a circle is given by the formula "C = pi x d" where "d" is the diameter and "pi" is the mathematical constant with an approximate value of 3.14.
In this problem, the diameter of the bicycle wheel is 60 centimeters, so its circumference is:
C = pi x d = 3.14 x 60 = 188.4 centimeters
When the wheel makes one revolution, it travels one circumference distance. Therefore, when the wheel makes 35 revolutions, it will travel:
distance = 35 x circumference = 35 x 188.4 = 6584 centimeters
We can convert centimeters to meters by dividing the distance by 100:
distance = 6584 ÷ 100 = 65.84 meters
Therefore, the wheel travels 65.84 meters when it makes 35 revolutions.
It costs James $4 to make an order of a dozen cookies. If he sells them for $20, what percentage is each order of cookies marked up?
HELP ASAP THANK YOU SO MUCH
A) 20%
B) 80%
C) 400%
D) 500%
Answers
Answer:
Step-by-step explanation:] Answer would be 400%
New value - Original Cost
Original value
= 20 - 4/4
= 16/4
= 4 x 100
= 400%
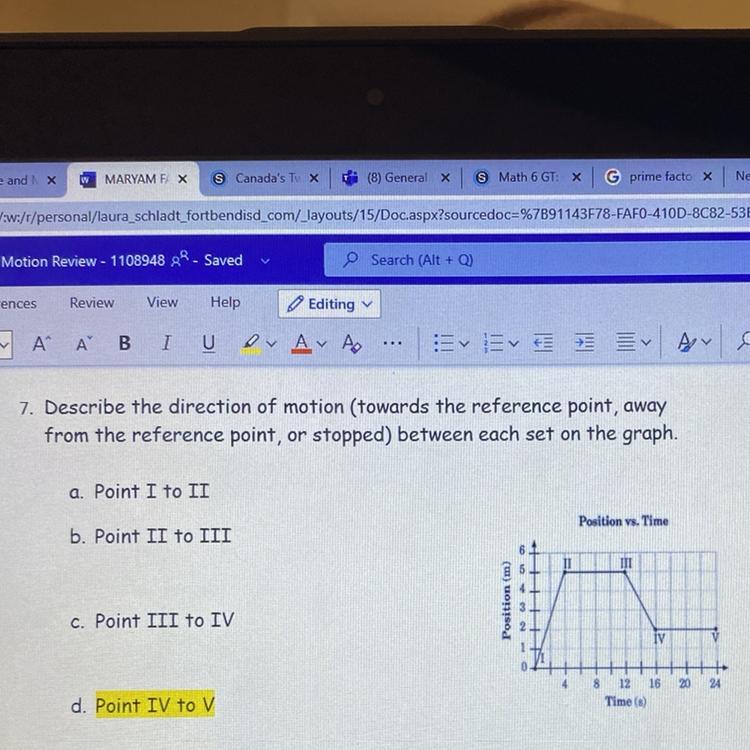
The midpoint of UV is point W. What are the
coordinates of point V?
10
8
O (8,9)
0 (-6, -14)
O (2, -23)
6
4
2
0 (s. ]
ㅇ [1]
2
4
6
8
10
X
-10 8 6 4 22
4 6
.
6
W 3.-7) 8
- 10

Answers
Answer:
(2,-23)
Step-by-step explanation:
It was just luck I'm starting Geometry this year.

The midpoint of line segment UV is given by M ( -11/2 , 1 )
What is the midpoint of two points?The midpoint of a line segment is a point that lies halfway between 2 points. The midpoint is the same distance from each endpoint.
Measure the distance between the two end points, and divide by 2.
Let A ( x₁ , y₁ ) be the first point
Let B ( x₂ , y₂ ) be the second point
The midpoint between A and B is M ( a , b ) where
a = ( x₁ + x₂ )/2
b = ( y₁ + y₂ ) / 2
Given data ,
Let the first point be U ( -8 , 9 )
Let the second point be V ( -3 , -7 )
Now , midpoint between U and V is M ( a , b ) where
a = ( x₁ + x₂ )/2
b = ( y₁ + y₂ ) / 2
On simplifying , we get
a = ( -8 + -3 ) / 2
b = ( 9 - 7 ) / 2
On further simplification , we get
a = -11/2
b = 1
Hence , the midpoint is M ( -11/2 , 1 )
To learn more about midpoint of two points click :
https://brainly.com/question/29155265
#SPJ7
How many terms of the sequence 10,12,14 will add up to 190
Answers
Answer:
required value is n = 10
Step-by-step explanation:
by ingnoring the negative value n = -14
Find the area of the triangle.
3 9
A
5
B
?] units²
![Find the area of the triangle.3 9A5B?] units](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/aWZMIZBnhz8tUKqZNrW2mkI5u8UBMICx.png)
Answers
The area of the triangle is 47.91 units²
How to find the area of the triangle?When all three sides of the triangle are known we can use Heron's formula. Consider the triangle ABC with sides a, b, and c has shown in the image.
Heron’s formula is:
Area =√s(s−a)(s−b)(s−c)
where,
a, b, c are the side length of the triangle
s is the semi-perimeter. s = (a+b+c)/2
In this case:
Using the knowledge of the radius of a circle. We can say:
a = BC = 3 + 9 = 12 units
b = AC = 5 + 3 = 8 units
c = AB = 5 + 9 = 14 units
s = (a+b+c)/2
s = (12+8+14)/2
s = 34/2
s = 17 units
Area = √s(s−a)(s−b)(s−c)
Area = √17(17−12)(17−8)(17−14)
Area = √17(5)(9)(3)
Area = √2295
Area = 47.91 units²
Learn more about area of triangle on:
https://brainly.com/question/1058720
#SPJ1
forty-nine percent of us teens have heard of a fax machine. you randomly select 12 us teens. find the probability that the number of these selected teens that have heard of a fax machine is exactly six (first answer listed below). find the probability that the number is more than 8 (second answer listed below). group of answer choices 0.225, 0.111 0.640, 0.175 0.640, 0.064 0.225, 0.064
Answers
The probability that the number of these selected teens that have heard of a fax machine is exactly six is 0.225 and the probability that the number is more than 8 is 0.064.
The first probability can be calculated using binomial distribution formula, where the number of success (teens who have heard of a fax machine) is 6 and the number of trials is 12. The probability of success is 0.49. The calculation is:
\((12 choose 6) * (0.49)^6 * (0.51)^(12-6) = 0.225\)
The second probability can be found by summing the probabilities of having more than 8 teens out of 12 who have heard of a fax machine. This can be calculated using binomial distribution formula for 9, 10, 11, and 12 success. The calculation is:
\((12 choose 9) * (0.49)^9 * (0.51)^(12-9) + (12 choose 10) * (0.49)^10 * (0.51)^(12-10) + (12 choose 11) * (0.49)^11 * (0.51)^(12-11) + (12 choose 12) * (0.49)^12 * (0.51)^(12-12)\\ = 0.064\)
So the answer is (0.225, 0.064).
Learn more about binomial :
https://brainly.com/question/11379135
#SPJ4
Can you pls help me
In the diagram,RS and PT are altitudes and m∠Q=68. Find m∠POR

Answers
Answer:
I believe it is 180
Step-by-step explanation:
All triangles add up to 180
Please explain your answer to the question in the picture with steps, thank you.

Answers
Answer:
(a) y = x/8
(b) y = 7/8
Step-by-step explanation:
You want a direct variation equation that relates x and y, given y = 2 when x = 16.
(a) Direct variationThe equation for direct variation is usually written in the form ...
y = kx
where k is the constant of proportionality.
The value of k can be found from ...
k = y/x . . . . divide by x
For the given values, k is ...
k = 2/16 = 1/8
The direct variation equation is ...
y = (1/8)x
(b) Find yThe value of y for x=7 is found by substituting 7 for x in the equation above:
y = (1/8)·7
y = 7/8
<95141404393>
According to Moore’s Law, the doubling time for the number of transistors that can be put on a computer chip is approximately two years. Recent data suggests that, as of 2013, the rate of growth predicted by Moore’s Law no longer holds. Growth has slowed to a doubling time of approximately three years. Find the new function that takes that longer doubling time into account with starting quantity A[0]. Enter the exact answer: f(t) =
Answers
The new function that takes that longer doubling time into account with starting quantity will be Aₙ = A₁ (1)ⁿ.
What is an exponent?Consider the function:
y = a (1 ± r)ˣ
Where x is the number of times this growth occurs, a = initial amount, and r = fraction by which this growth occurs.
As per Moore's Regulation, the multiplying time for the number of semiconductors that can be placed on a microprocessor is roughly two years. That's what ongoing information proposes, starting around 2013, the pace of development anticipated by Moore's Regulation does not hold anymore.
The rate is 0%, then the equation is given as,
Aₙ = A₁ (1 + 0)ⁿ
Aₙ = A₁ (1)ⁿ
The new function that takes that longer doubling time into account with starting quantity will be Aₙ = A₁ (1)ⁿ.
More about the exponent link is given below.
https://brainly.com/question/5497425
#SPJ1
y
X
Find the slope of the line that passes through the points
(2, -5) and (7, 1).
y
-5
6
2
7
1
Step 1: Choose (X1,Y1).
4
2.
-4
-2
2
4
6
8

Answers
Answer:
slope = \(\frac{6}{5}\)
Step-by-step explanation:
Calculate the slope m using the slope formula
m = \(\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\)
with (x₁, y₁ ) = (2, - 5) and (x₂, y₂ ) = (7, 1)
m = \(\frac{1+5}{7-2}\) = \(\frac{6}{5}\)
The required slope of the line passes through the points (2, -5) and (7, 1) is m = 6/5
What is the slope of the line?The slope of the line is a tangent angle made by line with horizontal. i.e. m =tanx where x in degrees.
here,
The slope of a line passing through two points (x1, y1) and (x2, y2) is given by the formula:
m = (y2 - y1) / (x2 - x1)
Let's apply this formula to the given points:
m = (1 - (-5)) / (7 - 2)
m = 6 / 5
Thus, the required slope of the line passes through the points (2, -5) and (7, 1).
Learn more about slopes here:
https://brainly.com/question/3605446
#SPJ7
A company has a policy of retiring company cars; this policy looks at number of miles driven, purpose of trips, style of car and other features. The distribution of the number of months in service for the fleet of cars is bell-shaped and has a mean of 64 months and a standard deviation of 7 months. Using the empirical (68-95-99.7) rule, what is the approximate percentage of cars that remain in service between 43 and 50 months?
Answers
Answer:
\( z =\frac{50-64}{7}= -2\)
\( z =\frac{43-64}{7}= -3\)
We know that within two deviations from the mean we have 95% of the data from the empirical rule so then below 2 deviation from the mean we have (100-95)/2 % =2.5%. And within 3 deviations from the mean we have 99.7% of the data so then below 3 deviations from the mean we have (100-99.7)/2% =0.15%
And then the final answer for this case would be:
\( 2.5 -0.15 = 2.35\%\)
Step-by-step explanation:
For this case we have the following parameters from the variable number of motnhs in service for the fleet of cars
\( \mu = 64, \sigma =7\)
For this case we want to find the percentage of values between :
\( P(43< X< 50)\)
And we can use the z score formula given by:
\( z = \frac{X-\mu}{\sigma}\)
In order to calculate how many deviation we are within from the mean. Using this formula for the limits we got:
\( z =\frac{50-64}{7}= -2\)
\( z =\frac{43-64}{7}= -3\)
We know that within two deviations from the mean we have 95% of the data from the empirical rule so then below 2 deviation from the mean we have (100-95)/2 % =2.5%. And within 3 deviations from the mean we have 99.7% of the data so then below 3 deviations from the mean we have (100-99.7)/2% =0.15%
And then the final answer for this case would be:
\( 2.5 -0.15 = 2.35\%\)
help! 16 is 40% of what?
Answers
Answer:
16 is 40% of 40
Step-by-step explanation:
16 = 40% x Y
16 = 40/100 x Y
y=3 x 100/40
y=40
FAST
Write two expressions to represent the following situation. Then, find the answer.
When Nathan went to bed, the outside temperature was 28°F. When he woke up the next morning, the temperature had decreased to -13°F. By how many degrees did the temperature change during the overnight hours
Answers
The temperature changed by 41°F during the overnight hours, decreasing from 28°F to -13°F.
How is an expression determined?The difference in temperature from 28°F to -13°F can be shown in one of two ways:
Temperature change equals final temperature - The starting temperatureTemperature change: (-13°F) - (28°F)Temperature change: -41°FTemperature change = final temperature minus initial temperature; temperature change = -13°F minus 28°F; temperature change = -41°F; temperature change = 41°F.To calculate the change in temperature, the first exponent equation subtracts the initial temperature from the end temperature. The change in this instance is negative and points to a drop in temperature.
The absolute value function is employed in the second statement to guarantee a positive result regardless of whether the temperature rose or fell. The result is the same as the first expression in this instance, but with a positive sign.
Learn more about Exponents here:
brainly.com/question/5497425
#SPJ1
enter solution set for following equation

Answers
Answer:
Step-by-step explanation:563765783+687546784-347657834=48589478w
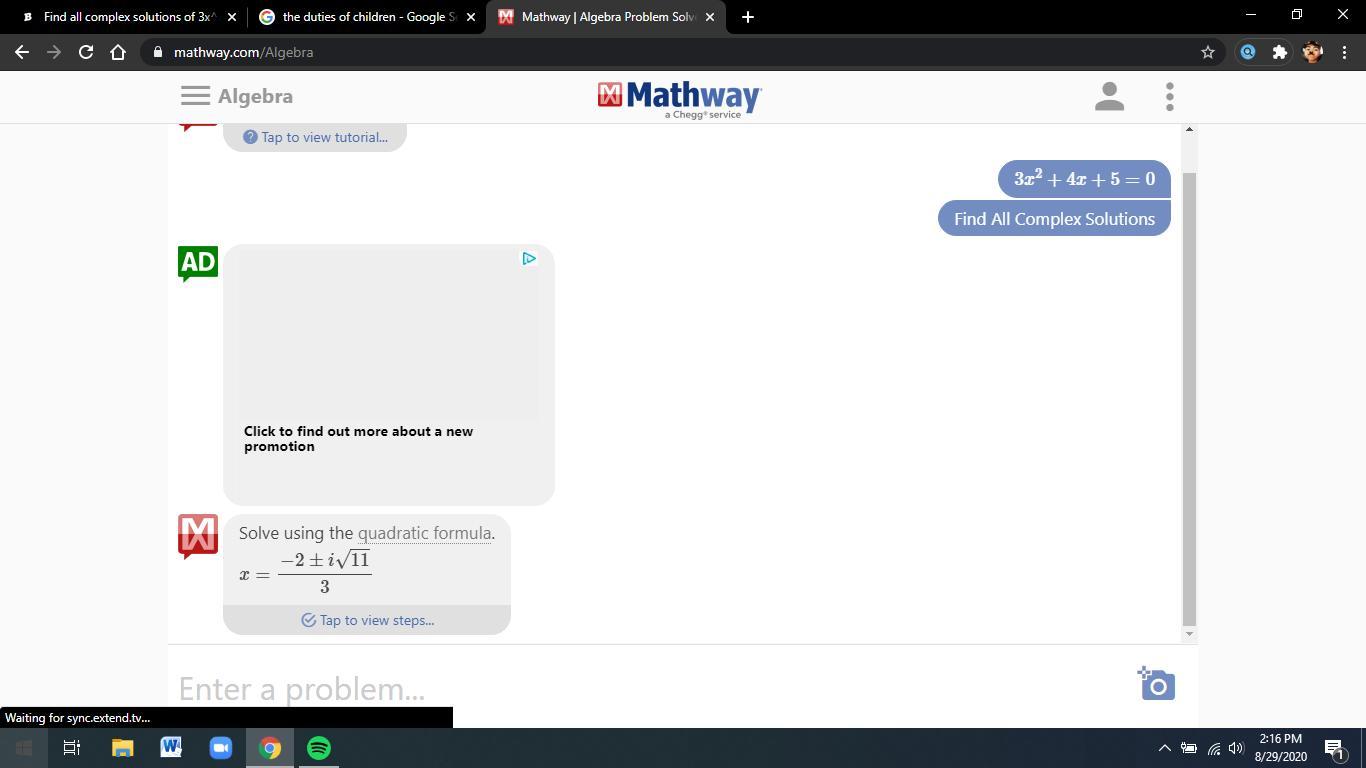
Find all complex solutions of 3x^2+4x+5=0 please guide!

Answers
Answer:
Step-by-step explanation:
a. Identify at least three cases in your daily life/work where the analytics could be applied.
b. Choose one of the cases and describe how you will approach the problem. For example, you can start from where/how you collect data, how to use the data, what kind of problem can be solved, and etc.
Answers
Explanation:
Remember, the term analytics (or data analytics) refers to the act of carefully examining raw data in other to observe if there are any trends.
a) The following are three cases in our daily life/work where analytics could be applied:
analyzing changes in cell phone charges based on call durationanalyzing changes in our sleeping pattern based on hours spent on electronic gadgetsanalyzing changes in train ticket sales based on the time of the day.b) For example, to analyze changes in my sleeping patterns based on hours spent on electronic gadgets, I need to first know
how many hours of sleep do I have every day in a particular period of time,how many hours have I spent on electronic gadgets daily for a period of time,Next, I need to answer based on the data; Is the amount of hours I sleep lower than expected? or Do I spend more time on electronic gadgets than sleep?what a literal ratio
Answers
Answer: The relationship in quantity, amount, or size between two or more things: proportion.
an open cone with base radius 28cm and perpendicular height 96cm was stretched to form sector of a circle. calculate the area
Answers
The area of the sector is 8800cm²
What is an area of the sector?
The area of the sector refers to the area encircled by a circle's sector. A sector always originates from the center of the circle.
What is curved surface area?
The area with just curved surfaces, leaving the circular top and base, is referred to as the curved surface area. Total Surface Area: This is the combined area of the bases and the curved surface.
Here, we have
Radius = 28cm, Height = 96cm
L² = 96² + 28²
= 9216 + 784
= 10000
L = √10000
= 100cm
curved surface area = πrl
= 22/7×28×100
= 8800cm²
area of cone = area of sector
area of sector = 8800cm2
Hence, the area of the sector is 8800cm²
To learn more about the area of the sector from the given link
https://brainly.com/question/22972014
#SPJ9
want to graph xdont you need to find out what x is?-3x-6y=0
Answers
We have a equation of a line in the form:
\(-3x-6y=0\)This goes through the point (0,0).
With another point, we can graph the line.
For example, for x=2, we have:
\(\begin{gathered} -3(2)-6y=0 \\ -6-6y=0 \\ -6y=6 \\ y=-1 \end{gathered}\)So the point (2,-1) belongs to the line.
We can graph the line passing through those points:

8) Solve the exponential equation

Answers
Answer:
5/8 =x
Step-by-step explanation:
2 ^ ( 3x-5) = ( 1/32) ^x
Rewriting 1/32 as 2 ^ -5
2 ^ ( 3x-5) = ( 2^-5) ^x
We know that a^b^c = a^ ( b*c)
2 ^ ( 3x-5) = ( 2) ^-5x
Setting the exponents equal
3x-5 = -5x
Subtract 3x from each side
3x-5-3x = -5x-3x
-5 = -8x
Divide each side by -8
-5/-8 = -8x/-8
5/8 =x
Rationalize the denominator 1/3√3
Answers
Answer:
Given,
1√3
by rationalizing,
1√3 ×(√3 / √3)
=√3/ 3
Step-by-step explanation: