Which of the following expressions demonstrates the distributive property?
Answers
Answer:
3(-8 + 1) = 3(-8) + 3(1)
Related Questions
The Customer Service Center in a large New York department store has determined that the amount of time spent with a customer about a complaint is normally distributed, with a mean of 10.1 minutes and a standard deviation of 2.8 minutes. What is the probability that for a randomly chosen customer with a complaint, the amount of time spent resolving the complaint will be as follows. (Round your answers to four decimal places.)(a) less than 10 minutes (b) longer than 5 minutes (c) between 8 and 15 minutes
Answers
Answer:
0.6395 ; 0.9657 ; 0.7333
Step-by-step explanation:
Given that:
Mean (m) = 10.1
Standard deviation (s) = 2.8
Obtain the following probabilities :
a) less than 10 minutes
P(x < 10)
Z = (x - m) / s
Z = (10 - 10.1) / 2.8
Z = 0.1 / 2.8
Z = 0.0357142
P(Z < 0.357) = 0.6395 ( Z probability calculator)
(b) longer than 5 minutes
P(x > 5)
Z = (x - m) / s
Z = (5 - 10.1) / 2.8
Z = −1.821428
P(Z < - 1.821) = 0.9657 ( Z probability calculator)
(c) between 8 and 15 minutes
P(8 < x < 15)
P(x < 8)
Z = (x - m) / s
Z = (8 - 10.1) / 2.8
Z = − 0.75
P(Z < - 0.75) = 0.22663 ( Z probability calculator)
P(x < 15)
Z = (x - m) / s
Z = (15 - 10.1) / 2.8
Z = 1.75
P(Z < 1.75) = 0.95994 ( Z probability calculator)
P(Z < 1.75) - P(Z < - 0.75)
0.95994 - 0.22663 = 0.7333
8 squared plus 6 squared = c squared using Pythagorean theorem for right triangle
Answers
Answer:
Hypotenuse of 10
Step-by-step explanation:
The Pythagorean Theorem is \(a^{2} +b^{2} = c^{2}\)
So let's plug in the numbers!
\(8^{2} +6^{2} = c^{2}\)
Let's start the squaring (8*8 and 6*6)
\(64 + 36 = c^{2}\)
Add the numbers to simplify
100 = \(c^{2}\)
To reverse/invert a number that is squared, all you have to do is to take the square root of the number. But we have to do the same operations on both sides of the equation.
\(\sqrt{100} =\sqrt{c^{2} }\)
We can simplify, and the square of c cancels because of the square root, leaving us with:
10 = c
Two investment portfolios are shown with the amount of money placed in each investment
and the ROR.
Investment
Tech Company Stock $2,800
Government Bond
$3,200
$950
$1,500
Junk Bond
Portfolio 1 Portfolio 2
Common Stock
O Portfolio 1 earns $31.77 more.
I
O Portfolio 2 earns $31.77 more.
O Portfolio 1 earns $69.17 more.
$1,275
$2,200
$865
$1,700
Which portfolio earns the most, and by how much?
Cortfolio 2 earns $69.17 more.
ROR
4.63%
-1.87%
2.50%
11.13%
Answers
Portfolio 1 earns $31.77 more than portfolio 2.
To compare the two portfolios, we need to calculate the rate of return (ROR) for each one. To do so, we can use the following formula:
ROR = (gain or loss / initial investment) x 100%
Let's calculate the ROR for each investment in portfolio 1:
Tech Company Stock: 4.63%
Government Bond: -1.87%
Junk Bond: 2.50%
Common Stock: 11.13%
To calculate the overall ROR for portfolio 1, we need to weight each investment by the amount invested. The total initial investment for portfolio 1 is:
= $2,800 + $3,200 + $950 + $1,500
= $8,450
The weighted average ROR for portfolio 1 is:
= (0.463 x $2,800 + (-0.0187) x $3,200 + 0.025 x $950 + 0.1113 x $1,500) / $8,450 x 100%
= 3.12%
Now let's do the same for portfolio 2:
Tech Company Stock: 2.50%
Government Bond: 11.13%
Junk Bond: 4.63%
Common Stock: -1.87%
The total initial investment for portfolio 2 is:
= $1,275 + $2,200 + $865 + $1,700
= $6,040
The weighted average ROR for portfolio 2 is:
= (0.025 x $1,275 + 0.1113 x $2,200 + 0.0463 x $865 + (-0.0187) x $1,700) / $6,040 x 100%
= 3.03%
Therefore, portfolio 1 earns $31.77 more than portfolio 2.
Learn more about Investment Plan here:
https://brainly.com/question/31781807
#SPJ1
In the triangle below, what is the length of BC ?
need help?!

Answers
Answer:
12
Step-by-step explanation:
just look at the other side since both are the same
What polynomial must be added to 3x^2 +4x + 7 to obtain a sum of 0?
Answers
Answer:
\( - 3x^2 - 4x - 7\)
Step-by-step explanation:
Let A should be added in the given polynomial to obtain a sum of zero.
Therefore,
\(A + 3 {x}^{2} + 4x + 7= 0 \\ \\ A = 0 - (3 {x}^{2} + 4x + 7 ) \\ \\ A = 0 - 3 {x}^{2} - 4x - 7 \\ \\ A = - 3 {x}^{2} - 4x - 7 \\ \)
Thus, \( - 3 {x}^{2} - 4x - 7\) should be added in the given polynomial to obtain a sum of zero.
The polynomial which must be added to 3x² +4x + 7 to obtain a sum of 0 is; -3x² -4x +7.
Let the polynomial which must be added to 3x² +4x + 7 to obtain a sum of 0 be represented by P.
In essence;
P + 3x² +4x + 7 = 0.By subtracting 3x² +4x + 7 from both sides of the equation to obtain the value of P; we have;
P = 0 -3x² -4x +7.Ultimately, P = -3x² -4x +7.
Read more on polynomials;
https://brainly.com/question/2833285
if the area of a circle is 36.2 square inches, find the length of its radius. (use 3.14 for pi) round to the nearest tenth. group of answer choices
Answers
if the area of a circle is 36.2 square inches, the radius of the circle to the nearest tenth is 3.4 inches.
The area of a circle is 36.2 square inches and we have to determine the radius of the circle to the nearest tenth.
The formula of the area of the circle is given as:
Area of circle = πR², where R is the radius of the circle.
We are given, Area of the circle = 36.2 square inches
So, πR² = 36.2 square inches
Now, π = 3.14
3.14R² = 36.2 square inches
R² = 36.2/3.14
R² = 11.53
Taking square root on both sides
R = √11.53
R = 3.39 inches
R ≈ 3.4 inch (Rounded to the nearest tenth)
Hence, the radius of the circle to the nearest tenth is 3.4 inches.
To learn more about circle here:
brainly.com/question/3683465
#SPJ4
Write the sentence as an equation. y multiplied by 184 is 395
Answers
Answer:
y * 184 = 395
Step-by-step explanation:
Answer:
184y = 395 should be the answer
Step-by-step explanation:
Please i need the answer fast k12
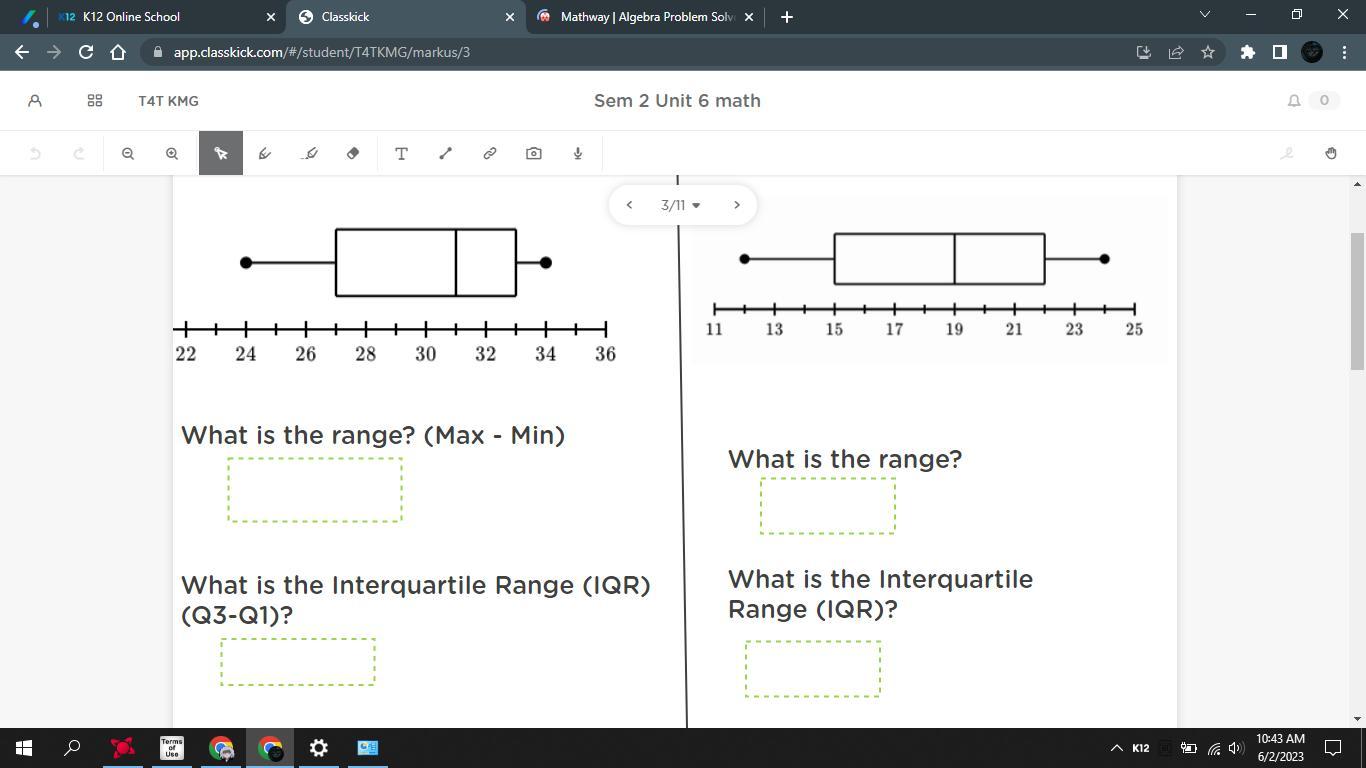
Answers
(A) The range and IQR for boxplot 1 is 10 and 6 respectively.
(B) The range and IQR for boxplot 2 is 12 and 7 respectively.
What is the IQR?The interquartile range defines the difference between the third and the first quartile.
The formula for the interquartile range is given below.
Interquartile range = Upper Quartile – Lower Quartile = Q3 – Q1
What is the range?The range is the difference between the lowest and highest values.
The formula for the interquartile range is given below.
Range = Maximum – Minimum
(A) For boxplot 1, we need to find the range and IQR from the given data set.
So, let 34 be the maximum and 24 be the minimum.
\(\text{Range}=\sf 34-24\)
\(\text{Range}=\sf10\)
Therefore, the range is 10.
Now time to find the IQR.
So, let 33 be Q3 and 27 be Q1.
\(\text{IQR}=\sf 33-27\)
\(\text{IQR}=\sf 6\)
Therefore, the IQR is 6.
(B) Now for boxplot 2, we will do the same thing as from part A.
Let's find the range.
So, let 24 be the maximum and 12 be the minimum.
\(\text{Range}=\sf 24-12\)
\(\text{Range}=\sf12\)
Hence, the range is 12.
Now for the IQR.
So, let 22 be Q3 and 15 be Q1.
\(\text{IQR}=\sf 22-15\)
\(\text{IQR}=\sf 7\)
Hence, the IQR is 7.
To know more about the range and IQR, visit:
https://brainly.com/question/31752116
#SPJ5
A mathematical hypothesis could be a guess at a _____ rule.options:inputvariablefunction
Answers
Given
A mathematical hypothesis could be a guess at a _____ rule.
To fill in the blanks.
Answer:
A mathematical hypothesis could be a guess at a function rule.
Sarah has been late for work 9 out of the last 30 days. Based on this, what is the probability that she will be on time for work on any given day? *
Answers
Answer:
30 %
______________________________________________________
The hypotenuse of the 30-60 right triangle is ____________, if the shortest side is x
1. x
2. x sqaure root 3
3. 2x
Answers
9514 1404 393
Answer:
3. 2x
Step-by-step explanation:
The side ratios of a 30-60-90 triangle are in the ratios ...
1 : √ : 2
The longest side is 2 times the length of the shortest side. If the shortest side is x, the longest side is 2x.
Which of the following is a solution to this inequality?
y<2/3x+2
(0, 3)
(−3, 1)
(3, 5)
(1, 2)
Answers
Answer:
(d) (1, 2)
Step-by-step explanation:
You want to know which of the given points satisfies the inequality.
GraphWe find it easiest to plot the given points on a graph of the solution. This shows us that (1, 2) is a solution to the inequality. (It lies in the solution area.)
__
Additional comment
Another way to choose the answer is to try each of the points in the inequality.
If you can visualize the boundary line (without plotting it) as a line with positive slope and a y-intercept of 2, you can more readily reject the first choice and accept the last choice. (0, 3) is above the y-intercept, and (1, 2) is to the right of it (in the solution space).
You may also recognize the x-intercept will be -3, so the second choice lies above the boundary line.

Which sequence of transformations was applied to the parent tangent function to create the function m(x) = 2tan(3x+4)
Answers
The function m(x) = 2tan(3x+4) is obtained by applying a sequence of transformations to the parent tangent function.
To determine the sequence of transformations, let's break down the given function:
1. Inside the tangent function, we have the expression (3x+4). This represents a horizontal compression and translation.
2. The coefficient 3 in front of x causes the function to compress horizontally by a factor of 1/3. This means that the period of the function is shortened to one-third of the parent tangent function's period.
3. The constant term 4 inside the parentheses shifts the function horizontally to the left by 4 units. So, the graph of the function is shifted to the left by 4 units.
4. Outside the tangent function, we have the coefficient 2. This represents a vertical stretch.
5. The coefficient 2 multiplies the output of the tangent function by 2, resulting in a vertical stretch. This means that the graph of the function is stretched vertically by a factor of 2.
In summary, the sequence of transformations applied to the parent tangent function to create the function m(x) = 2tan(3x+4) is a horizontal compression by a factor of 1/3, a horizontal shift to the left by 4 units, and a vertical stretch by a factor of 2.
Example:
Let's consider a point on the parent tangent function, such as (0,0), which lies on the x-axis.
After applying the transformations, the corresponding point on the function m(x) = 2tan(3x+4) would be:
(0,0) -> (0,0) (since there is no vertical shift in this case)
This example helps illustrate the effect of the transformations on the graph of the function.
For more question on expression
https://brainly.com/question/1859113
#SPJ8
Cheeseburgers to go has advertised for counter help. If you take the job, you will be working 18 hours
a week for $69.20 per week. How much would you make an hour?
Answers
Answer:
about $3.84
Step-by-step explanation:
you do 69.20 divided by 18
Consider the ordinary differential equation (answer questions in picture)

Answers
a. Given the 2nd order ODE
\(y''(x) = 4y(x) + 4\)
if we substitute \(z(x)=y'(x)+2y(x)\) and its derivative, \(z'(x)=y''(x)+2y'(x)\), we can eliminate \(y(x)\) and \(y''(x)\) to end up with the ODE
\(z'(x) - 2y'(x) = 4\left(\dfrac{z(x)-y'(x)}2\right) + 4\)
\(z'(x) - 2y'(x) = 2z(x) - 2y'(x) + 4\)
\(\boxed{z'(x) = 2z(x) + 4}\)
and since \(y(0)=y'(0)=1\), it follows that \(z(0)=y'(0)+2y(0)=3\).
b. I'll solve with an integrating factor.
\(z'(x) = 2z(x) + 4\)
\(z'(x) - 2z(x) = 4\)
\(e^{-2x} z'(x) - 2 e^{-2x} z(x) = 4e^{-2x}\)
\(\left(e^{-2x} z(x)\right)' = 4e^{-2x}\)
\(e^{-2x} z(x) = -2e^{-2x} + C\)
\(z(x) = -2 + Ce^{2x}\)
Since \(z(0)=3\), we find
\(3 = -2 + Ce^0 \implies C=5\)
so the particular solution for \(z(x)\) is
\(\boxed{z(x) = 5e^{-2x} - 2}\)
c. Knowing \(z(x)\), we recover a 1st order ODE for \(y(x)\),
\(z(x) = y'(x) + 2y(x) \implies y'(x) + 2y(x) = 5e^{-2x} - 2\)
Using an integrating factor again, we have
\(e^{2x} y'(x) + 2e^{2x} y(x) = 5 - 2e^{2x}\)
\(\left(e^{2x} y(x)\right)' = 5 - 2e^{2x}\)
\(e^{2x} y(x) = 5x - e^{2x} + C\)
\(y(x) = 5xe^{-2x} - 1 + Ce^{-2x}\)
Since \(y(0)=1\), we find
\(1 = 0 - 1 + Ce^0 \implies C=2\)
so that
\(\boxed{y(x) = (5x+2)e^{-2x} - 1}\)
6.a) The differential equation for z(x) is z'(x) = 2z(x) + 4, z(0) = 3.
6.b) The value of z(x) is \(z(x) = 5e^{2x} - 2\).
6.c) The value of y(x) is \(y(x) = \frac{5e^{2x}}{4} - \frac{1}{4e^{2x}} -1\).
The given ordinary differential equation is y''(x) = 4y(x) + 4, y(0) = y'(0) = 1 ... (d).
We are also given a substitution function, z(x) = y'(x) + 2y(x) ... (z).
Putting x = 0, we get:
z(0) = y'(0) + 2y(0),
or, z(0) = 1 + 2*1 = 3.
Rearranging (z), we can write it as:
z(x) = y'(x) + 2y(x),
or, y'(x) = z(x) - 2y(x) ... (i).
Differentiating (z) with respect to x, we get:
z'(x) = y''(x) + 2y'(x),
or, y''(x) = z'(x) - 2y'(x) ... (ii).
Substituting the value of y''(x) from (ii) in (d) we get:
y''(x) = 4y(x) + 4,
or, z'(x) - 2y'(x) = 4y(x) + 4.
Substituting the value of y'(x) from (i) we get:
z'(x) - 2y'(x) = 4y(x) + 4,
or, z'(x) - 2(z(x) - 2y(x)) = 4y(x) + 4,
or, z'(x) - 2z(x) + 4y(x) = 4y(x) + 4,
or, z'(x) = 2z(x) + 4y(x) - 4y(x) + 4,
or, z'(x) = 2z(x) + 4.
The initial value of z(0) was calculated to be 3.
6.a) The differential equation for z(x) is z'(x) = 2z(x) + 4, z(0) = 3.
Transforming z(x) = dz/dx, and z = z(x), we get:
dz/dx = 2z + 4,
or, dz/(2z + 4) = dx.
Integrating both sides, we get:
∫dz/(2z + 4) = ∫dx,
or, {ln (z + 2)}/2 = x + C,
or, \(\sqrt{z+2} = e^{x + C}\),
or, \(z =Ce^{2x}-2\) ... (iii).
Substituting z = 3, and x = 0, we get:
\(3 = Ce^{2*0} - 2\\\Rightarrow C - 2 = 3\\\Rightarrow C = 5.\)
Substituting C = 5, in (iii), we get:
\(z = 5e^{2x} - 2\).
6.b) The value of z(x) is \(z(x) = 5e^{2x} - 2\).
Substituting the value of z(x) in (z), we get:
z(x) = y'(x) + 2y(x),
or, 5e²ˣ - 2 = y'(x) + 2y(x),
which gives us:
\(y(x) = \frac{5e^{2x}}{4} - \frac{1}{4e^{2x}} -1\) for the initial condition y(x) = 0.
6.c) The value of y(x) is \(y(x) = \frac{5e^{2x}}{4} - \frac{1}{4e^{2x}} -1\).
Learn more about differential equations at
https://brainly.com/question/18760518
#SPJ1
Use the image to determine the direction and angle of rotation. Graph of triangle ABC in quadrant 1 with point A at 1 comma 3. A second polygon A prime B prime C prime in quadrant 4 with point A prime at 3 comma negative 1. 90° clockwise rotation 180° clockwise rotation 180° counterclockwise rotation 90° counterclockwise rotation
Answers
First, we can find the translation vector that moves point A to point A':
translation vector = A' - A = (3, -1) - (1, 3) = (2, -4)
Next, we can find the vector that connects point B to point A in the original triangle ABC:
vector AB = B - A
Then, we can rotate this vector using the rotation matrix for the desired angle of rotation:
90° clockwise rotation:
|0 -1| |x| |y'|
|1 0| * |y| = | -x'|
180° clockwise rotation:
|-1 0| |x| |x'|
| 0 -1| * |y| = |y'|
180° counterclockwise rotation:
|-1 0| |x| |-x'|
| 0 -1| * |y| = |-y'|
90° counterclockwise rotation:
| 0 1| |x| |-y'|
|-1 0| * |y| = | x'|
Finally, we can add the translation vector to the rotated vector to get the coordinates of the corresponding point in the new polygon A' B' C':
90° clockwise rotation: B' = A' + (AB rotated 90° clockwise + translation)
180° clockwise rotation: B' = A' + (AB rotated 180° clockwise + translation)
180° counterclockwise rotation: B' = A' + (AB rotated 180° counterclockwise + translation)
90° counterclockwise rotation: B' = A' + (AB rotated 90° counterclockwise + translation)
Using this method, we can find the coordinates of points B' and C' in the new polygon A' B' C'. Then, we can use the coordinates of these points to determine the direction and angle of rotation needed to move the original triangle to the new polygon.
the 3rd term of a linear sequence is 17. the 45th term is 269. determine the formula for the nth term.
Answers
Step-by-step explanation:
a linear or arithmetic sequence has a start value as first term, and then every following term is created by adding the same constant to the previous term.
a1 = a
a2 = a1 + c = a + c
a3 = a2 + c = a + c + c = a + 2c
a4 = a3 + c = a + c + c + c = a + 3c
...
as we can easily see
an = an-1 + c = a + (n-1)c
in our case
a3 = 17 = a + 2c
a = 17 - 2c
a45 = 269 = a + 44c = 17 - 2c + 44c = 17 + 42c
252 = 42c
c = 6
a = 17 - 2c = 17 - 2×6 = 17 - 12 = 5
so,
an = 5 + (n-1)×6
someone pls help me asap!! :((

Answers
Step-by-step explanation:
To graph them, sub 2 random x/y numbers and find the corresponding coordinates then plot these 2 points on the axes then connect to form a straight line :)
Topic: coordinate geometry
If you like to venture further, feel free to check out my insta (learntionary). It would be best if you could give it a follow. I'll be constantly posting math tips and notes! Thanks!
solve 3(x+4)-11=28 please
Answers
Answer:
\(\huge\boxed{\sf x = 9}\)
Step-by-step explanation:
Given equation:3(x + 4) - 11 = 28
Add 28 to both sides3(x + 4) = 28 + 11
3(x + 4) = 39
Distribute3x + 12 = 39
Subtract 12 from both sides3x = 39 - 12
3x = 27
Divide both sides by 3x = 27/3
x = 9\(\rule[225]{225}{2}\)
Solve 1/3(3.2×1.4)2.8
Simplify your answer
Answers
Answer:
4.181
Step-by-step explanation:
1/3 (3.2×1.4) 2.8
1/3 ( 4.48) 2.8
1/3 (4.48 × 2.8)
1/3 × 12.544
= 4.181
Explain in words the graphical transformations that f(x) undergoes to become
f(x + 9) − 1.
Answers
The transformations taking place in the given function is a horizontal left ward shift of 9 units and 1 unit upward vertical shift.
What is transformation?A Transformation in Math is a process of moving an object (two-dimensional shape) from its original position to a new position.
Given that, a function f(x) undergo some transformations to become f(x+9)-1,
We know that,
Vertical Shifting:
Adding a constant to a function will shift its graph vertically (i.e. y = f (x) + c). Adding a positive constant c will shift the graph upward c units, while adding a negative constant c will shift it downward c units.
Horizontal Shifting:
Horizontal shifts are inside changes that affect the input (x-) axis values and shift the function left or right. Combining the two types of shifts will cause the graph of a function to shift up or down and right or left.
Therefore, there is transformation of a horizontal and vertical shift.
Hence, the transformations taking place in the given function is a horizontal left ward shift of 9 units and 1 unit upward vertical shift.
Learn more about transformations, click;
https://brainly.com/question/29194193
#SPJ9
(question 15) Find the derivative of the function
using logarithmic differentiation.

Answers
Answer:
\(\textsf{A.} \quad (2+x)^x\left[\dfrac{x}{2+x}+\ln(2+x)\right]\)
Step-by-step explanation:
Replace f(x) with y in the given function:
\(y=(x+2)^x\)
Take natural logs of both sides of the equation:
\(\ln y=\ln (x+2)^x\)
\(\textsf{Apply the log power law to the right side of the equation:} \quad \ln a^n=n \ln a\)
\(\ln y=x\ln (x+2)\)
Differentiate using implicit differentiation.
Place d/dx in front of each term of the equation:
\(\dfrac{\text{d}}{\text{d}x}\ln y=\dfrac{\text{d}}{\text{d}x}x\ln (x+2)\)
First, use the chain rule to differentiate terms in y only.
In practice, this means differentiate with respect to y, and place dy/dx at the end:
\(\dfrac{1}{y}\dfrac{\text{d}y}{\text{d}x}=\dfrac{\text{d}}{\text{d}x}x\ln (x+2)\)
Now use the product rule to differentiate the terms in x (the right side of the equation).
\(\boxed{\begin{minipage}{5.5 cm}\underline{Product Rule for Differentiation}\\\\If $y=uv$ then:\\\\$\dfrac{\text{d}y}{\text{d}x}=u\dfrac{\text{d}v}{\text{d}x}+v\dfrac{\text{d}u}{\text{d}x}$\\\end{minipage}}\)
\(\textsf{Let}\; u=x \implies \dfrac{\text{d}u}{\text{d}x}=1\)
\(\textsf{Let}\; v=\ln(x+2) \implies \dfrac{\text{d}v}{\text{d}x}=\dfrac{1}{x+2}\)
Therefore:
\(\begin{aligned}\dfrac{1}{y}\dfrac{\text{d}y}{\text{d}x}&=x\cdot \dfrac{1}{x+2}+\ln(x+2) \cdot 1\\\\\dfrac{1}{y}\dfrac{\text{d}y}{\text{d}x}&= \dfrac{x}{x+2}+\ln(x+2)\end{aligned}\)
Multiply both sides of the equation by y:
\(\dfrac{\text{d}y}{\text{d}x}&=y\left( \dfrac{x}{x+2}+\ln(x+2)\right)\)
Substitute back in the expression for y:
\(\dfrac{\text{d}y}{\text{d}x}&=(x+2)^x\left( \dfrac{x}{x+2}+\ln(x+2)\right)\)
Therefore, the differentiated function is:
\(f'(x)=(x+2)^x\left[\dfrac{x}{x+2}+\ln(x+2)\right]\)
\(f'(x)=(2+x)^x\left[\dfrac{x}{2+x}+\ln(2+x)\right]\)
hi, please help me, i really need it
thanks

Answers
Exterior Angle Inequality Theorem
\( \normalsize\blue{\overline{\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad \ \ \ }}\)
Direction:
Use the Exterior Angle Inequality Theorem to find the measure of each angle below.
Answer:
\( \huge \underline{\boxed{\sf \red{ \angle C = 27^{\circ} }}}\)
\( \huge \underline{\boxed{\sf \red{ \angle D = 153^{\circ} }}}\)
Solution:
Add the ∠A and ∠B and minus it to 180° to know the measure of ∠C. To find the ∠D add only the ∠A and ∠B.
Finding ∠C
\(\large\tt{{180}^{\circ} = \angle A + \angle B + \angle C}\)
\(\large\tt{{180}^{\circ} = {35}^{\circ} + {118}^{\circ} + \angle C }\)
\(\large\tt{{180}^{\circ} = {153}^{\circ} + \angle C }\)
\(\large\tt{{180}^{\circ} - {153}^{\circ} = \angle C }\)
\(\large\tt{{27}^{\circ} = \angle C }\)
\(\large{\boxed{\tt{\angle C = {27}^{\circ}}} }\)
Finding ∠D or ∠ACD
\(\large\tt{ \angle A + \angle B = \angle ACD }\)
\(\large\tt{ {35}^{\circ} + {118}^{\circ} = \angle ACD }\)
\(\large\tt{ {153}^{\circ} = \angle ACD }\)
\(\large{\boxed{\tt{\angle ACD = {153}^{\circ} }}}\)
\( \normalsize\blue{\overline{\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad \ \ \ }}\)
\( \\ \)
#CarryOnLearning
Write an equation of variation to represent the situation and solve for the missing information The time to complete a project varies inversely with the number of employees. If 3 peoplecan complete the project in 7 days, how long will it take 5 people?
Answers
the relation between the days and number of employee is inverse relation,
so,
\(D\propto\frac{1}{n}\)here D = days,
n = no. of employees.
\(D=\frac{k}{n}\)put D = 3 and n = 7
\(\begin{gathered} 3=\frac{k}{7} \\ k=21 \end{gathered}\)so for n = 5
\(\begin{gathered} D=\frac{k}{5} \\ D=\frac{21}{5} \\ D=4.2\text{ days} \end{gathered}\)it will take 4.2 days if 5 people do it.
52(7)^1/5
Need help solving this problem. I don’t have Ti-84 Calculator yet
Answers
Answer:
\(52 \sqrt[5]{7} \)
Step-by-step explanation:
\(52(7 {)}^{ \frac{1}{5} } \)
\( = 52 \sqrt[5]{7} \)
Two vectors ...and ...with ... and ..., have an angle of ... between them. Determine .. to the nearest hundredth by drawing a parallelogram. Be sure to show and explain all work.

Answers
(m + n) has a magnitude of approximately 25.8.
We have,
Consider the two vectors as m and n.
To find (m + n), we need to add the two vectors.
To do this, we first need to determine the components of each vector.
Let's call the angle between vector m and the x-axis α, and the angle between vector n and the x-axis β.
Then we have:
|m| = 10, so the x-component of vector m is m_x = 10 cos α and the
y-component is m_y = 10 sin α.
|n| = 15, so the x-component of vector n is n_x = 15 cos β and the
y-component is n_y = 15 sin β.
We also know that the angle between vectors m and n is 75 degrees. Using the dot product, we can find the cosine of this angle:
m · n = |m| |n| cos 75
m · n = 10 * 15 * cos 75
m · n = 37.32
We also know that the dot product is equal to the sum of the products of the corresponding components:
m · n = (m_x) x (n_x) + (m_y) x (n_y)
37.32 = 10 cos α x 15 cos β + 10 sin α * 15 sin β
Now we have two equations with two unknowns:
m_x + n_x = (10 cos α) + (15 cos β)
m_y + n_y = (10 sin α) + (15 sin β)
We can solve for α and β using the equations we just derived:
m_x + n_x = (10 cos α) + (15 cos β)
10 cos α = (m_x + n_x - 15 cos β)
cos α = (m_x + n_x - 15 cos β) / 10
α = arccos[(m_x + n_x - 15 cos β) / 10]
m_y + n_y = (10 sin α) + (15 sin β)
10 sin α = (m_y + n_y - 15 sin β)
sin α = (m_y + n_y - 15 sin β) / 10
α = arcsin[(m_y + n_y - 15 sin β) / 10]
Now we can substitute these values into the equations for m_x + n_x and m_y + n_y to find (m + n):
m_x + n_x = 10 cos α + 15 cos β
m_y + n_y = 10 sin α + 15 sin β
We can use a graphical method to estimate the values of α and β. Start by drawing vector m with length 10 and angle α with respect to the x-axis. Then draw vector n with length 15 and angle β with respect to the x-axis, starting the tail of n at the head of m.
The parallelogram formed by the two vectors will have a diagonal that represents (m + n). Use a ruler to measure the length of this diagonal to the nearest hundredth.
We can use the law of cosines to find the magnitude of (m + n):
|(m + n)|² = |m|² + |n|² + 2|m||n| cos 75
|(m + n)|² = 10² + 15² + 2(10)(15) cos 75
|(m + n)|² = 665.19
|(m + n)| = 25.8 (to the nearest hundredth)
Therefore,
(m + n) has a magnitude of approximately 25.8.
Learn more about vectors here:
https://brainly.com/question/14390388
#SPJ1
for each parallel lines. you are given the measure of one angle
Answers
Answer:
The question is not complete
Find an equation of the line having y-intercept (0,1) and x-intercept (-6,0)
Answers
Answer:
x-6y+6=0
Step-by-step explanation:
solution file attached

The equation for a line given slope and y-intercept is y = mx + b
M is slope, and B is y-intercept.
To find slope, use this formula.
\(\frac{y2 - y1}{x2 - x2}\)
\(\frac{0-1}{-6 - 0}\)
-1/-6 = 1/6
y = 1/6x + 1
The ESS Ravens bought pizza for $900 to sell at the football game. They kept 10 pizzas to feed the players after the game and sold the rest for $1040. There were 8 slices in each pizza. Their profit was 50 cents a slice.
a) How many pizzas were in the original order?
Answers
Answer: 45
Step-by-step explanation:
The total profit in all was \(1040-900=\$ 140\).
The total profit per pizza was \((0.50)(8)=\$4\).
This means they sold \(\frac{140}{4}=35\) pizzas.
Adding this to the 10 pizzas held back, there were \(35+10=45\) pizzas in the original order.
Find the surface area of the box shown
