Which of the following expressions are equivalent to x - (-x) + y?
Choose all the answers that apply.
A. 0+y
B. y
C. None of the above
Answers
The expression equivalent to x - (-x) + y is 2x + y.
The correct option is (C) None of the above
What is expression?An expression is a combination of numbers, variables, functions (such as addition, subtraction, multiplication or division etc.)
Given:
x - (-x) + y
=x +x +y
= X(1+1) + y
= x(2) + y
= 2x + y
Hence, the equivalent expression is 2x + y.
Learn more about expression here:
https://brainly.com/question/14083225
#SPJ1
Related Questions
1 kk (a) Prove that every positive integer k satisfies 5 = k+I + X(+1) + (b) Prove that there exist integers a 3 there exist n integers dj < a2 <...< an such that a 1 1 1 1 + + a1 a2 + an
Answers
a) We have shown that for every positive integer k, 1/k = 1/(k+1) + 1/(k(k+1)). b) We have found integers a = 2, b = 3, and c = 6 such that 1 = 1/a + 1/b + 1/c. c) The every integer n ≥ 3, there exist n integers a₁, a₂, ..., aₙ such that 1 = 1/a₁ + 1/a₂ + ... + 1/aₙ.
(a) To prove that every positive integer k satisfies 1/k = 1/(k+1) + 1/(k(k+1)), we can start by manipulating the right-hand side of the equation:
1/(k+1) + 1/(k(k+1))
= (k/(k(k+1))) + 1/(k(k+1)) (finding a common denominator)
= (k + 1)/(k(k+1)) (combining the fractions with the same denominator)
= 1/k (canceling out the common factor of (k+1) in the numerator and denominator)
Thus, we have shown that for every positive integer k, 1/k = 1/(k+1) + 1/(k(k+1)).
(b) To prove that there exist integers a < b < c such that 1 = 1/a + 1/b + 1/c, we can choose specific values for a, b, and c. Let's choose a = 2, b = 3, and c = 6:
1/2 + 1/3 + 1/6
= 3/6 + 2/6 + 1/6
= 6/6
= 1
Therefore, we have found integers a = 2, b = 3, and c = 6 such that 1 = 1/a + 1/b + 1/c.
(c) To prove that for every integer n ≥ 3, there exist n integers a₁, a₂, ..., aₙ such that 1 = 1/a₁ + 1/a₂ + ... + 1/aₙ, we can use the following construction:
Choose a₁ = 2, a₂ = 3, and a₃ = 6 as shown in part (b) above.
Now, for the remaining integers a₄, a₅, ..., aₙ, we can choose them to be equal to the least common multiple (LCM) of a₁, a₂, ..., aₙ₋₁. This guarantees that each term 1/aₖ, where k > 3, will have the same denominator and can be added to the other terms.
Since the LCM is a multiple of each of the previous integers, it is guaranteed that the sum of the reciprocals will be equal to 1.
Therefore, for every integer n ≥ 3, there exist n integers a₁, a₂, ..., aₙ such that 1 = 1/a₁ + 1/a₂ + ... + 1/aₙ.
The complete question is:
(a) Prove that every positive integer k satisfies 1/k=1/(k+1) + 1/ (k(k+1)).
(b) Prove that there exist integers a <b<c such that 1 = 1/a + 1/b + 1/c.
(c) Prove that for every integer n ≥ 3 there exist n integers \(a_1,a_2,.....,a_n\) such that \(1=1/a_1+1/a_2+.....1/a_n\)
To know more about integer:
https://brainly.com/question/490943
#SPJ4
a pizza parlor in tallahassee sells a pizza with a 16-inch diameter. a pizza parlor in jaco, costa rica, sells a pizza with a 27.8-centimeter diameter. part a: how many square inches of pizza is the pizza from tallahassee? show every step of your work. (1 point) part b: how many square centimeters of pizza is the pizza from jaco, costa rica? show every step of your work. (1 point) part c: if 1 in.
Answers
In part a, we will calculate the number of square inches in a pizza with a 16-inch diameter. In part b, we will calculate the number of square centimeters in a pizza with a 27.8-centimeter diameter.
Part a: To find the area of the pizza in square inches, we need to calculate the area of a circle with a diameter of 16 inches. The formula for the area of a circle is \(A=\pi r^2\), where r is the radius. Since the diameter is given, we can find the radius by dividing the diameter by 2. So, the radius of the pizza is 16/2 = 8 inches. Plugging this value into the formula, we get \(A = \pi (8^2) = 64\pi\) square inches.
Part b: To find the area of the pizza in square centimeters, we need to calculate the area of a circle with a diameter of 27.8 centimeters. Again, we use the formula \(A=\pi r^2\), but this time we need the radius in centimeters. The radius is 27.8/2 = 13.9 centimeters. Plugging this value into the formula, we get \(A = \pi (13.9^2) = 191.04\pi\) square centimeters.
Part c: To convert the area from part a (in square inches) to square centimeters, we need to know the conversion factor. Given that 1 inch is equal to 2.54 centimeters, we can square this conversion factor to get the conversion factor for area.
So, 1 square inch is equal to \((2.54)^2 = 6.4516\) square centimeters. Multiplying the area from part a (64π square inches) by the conversion factor, we get 64π * 6.4516 square centimeters, which simplifies to 412.96π square centimeters.
Therefore, the pizza from Tallahassee has an area of 64π square inches, the pizza from Jaco, Costa Rica has an area of 191.04π square centimeters, and the conversion of the pizza from Tallahassee to square centimeters is approximately 412.96π square centimeters.
Learn more about diameter here:
https://brainly.com/question/17134037
#SPJ11
ILL GIVE BRAINLIEST PLEASE HELP ASAP

Answers
Answer:
Dan made more
Step-by-step explanation:
Dan: 227×70=15,890 15% of 15,890 is 2,383.50
Mike:251×90=22,590 15% of 22,590 is 2,259
Identify the interval of increase of the given function.
Answers
Answer
The interval of increase of the given function is x > -2.5.
This can be written in interval form as (-2.5, ∞)
Explanation
The interval of increase of the function refers to the range of values of the independent variable (x), where the graph is sloping positively, that is, the region of the graph that shows where the dependent variable (y) is increasing.
From the graph, we can see that the graph slopes negatively, that is, the values of y keep decreasing as we move from left to right at values of x less than -2.5, but at the point where x = -2.5, the sloping changes (this point is called the vertex of the graph or function; it is the point where the graph changes from increasing to decreasing or from decreasing to increasing).
We can also see that at values of x greater than -2.5, the graph slopes positively and the values of y increases as we move from left to right.
So, the interval of increase of the given function is x > -2.5.
This can be written in interval form as (-2.5, ∞)
Hope this Helps!!!
If one load of laundry through a hotel service
costs $15.37, how much will 12 loads cost, if there
are no quantity discounts?
Answers
Answer:
$$184.44
Step-by-step explanation:
Answer:
$184.44
Step-by-step explanation:
If one load cost $15.37 and you have to do 12 loads then it would be 15.37 for each load so you would do $15.37 times 12 loads and you would have spent $184.44.
Point P is located 3/5 of the way from point A to point E. Point A is located at (-1, -1) and point P is located
at (-7,5). What are the coordinates for point E?
Answers
By using the line segment formula, we conclude that the coordinates of point E are E(x, y) = (- 11, 9).
How to determine the coordinates of the missing endpoint of a line segment
In this problem we find a line segment of which the coordinates of an endpoint and a point within the segment and in accordance with a segment ratio are known. The coordinates of the other endpoint must be found in accordance with the following expression:
E(x, y) = A(x, y) + k · [P(x, y) - A(x, y)] (1)
Where E(x, y) is the missing endpoint.
If we know that A(x, y) = (- 1, - 1), P(x, y) = (- 7, 5) and k = 5 / 3, then the coordinates of point E are:
E(x, y) = (- 1, - 1) + (5 / 3) · [(- 7, 5) - (- 1, - 1)]
E(x, y) = (- 1, - 1) + (5 / 3) · (- 6, 6)
E(x, y) = (- 1, - 1) + (- 10, 10)
E(x, y) = (- 11, 9)
To learn more on partioning line segments: https://brainly.com/question/3148758
#SPJ1

Factor completely 5x2 - 20.
Answers
Answer:
\(5(x-2)(x+2)\)
Step-by-step explanation:
Factor out 5:
\(5(x^2-4)\)
Use difference of squares formula for the inside:
\(5(x-2)(x+2)\)
Help meeeeee with number 6, 8, 10 pls

Answers
6) -x - 4
8) 21ab - 14ac + 28
10)
\( \frac{x - 24}{6} \)
Sketch a graph of each of the four angles in the same coordinate plane. Label the ordered pairs that intersect the circle. The angles given are 30°, 150°, 210°, 330°
Answers
To Sketch a graph of each of the four angles of 30°, 150°, 210°, 330°, one can follow the example that is given in the image.
What is a sketch?In the mathematics, a sketch is known to be a given category that tells what a thing is all about.
Note that in sketching, one need to take not of the key points and angles and as such, To Sketch a graph of each of the four angles of 30°, 150°, 210°, 330°, one can follow the example that is given in the image.
Learn more about angles from
https://brainly.com/question/25770607
#SPJ1

What is the length of the curve with parametric equations x = t - cos(t), y = 1 - sin(t) from t = 0 to t = π? (5 points)
A) 8
B) 4 times the square root of 2
C) 4
D) 8 times the square root of 2
Answers
Answer:
B) 4√2
General Formulas and Concepts:
Calculus
Differentiation
DerivativesDerivative NotationBasic Power Rule:
f(x) = cxⁿf’(x) = c·nxⁿ⁻¹Parametric Differentiation
Integration
IntegralsDefinite IntegralsIntegration Constant CArc Length Formula [Parametric]: \(\displaystyle AL = \int\limits^b_a {\sqrt{[x'(t)]^2 + [y(t)]^2}} \, dx\)
Step-by-step explanation:
Step 1: Define
Identify
\(\displaystyle \left \{ {{x = t - cos(t)} \atop {y = 1 - sin(t)}} \right.\)
Interval [0, π]
Step 2: Find Arc Length
[Parametrics] Differentiate [Basic Power Rule, Trig Differentiation]: \(\displaystyle \left \{ {{x' = 1 + sin(t)} \atop {y' = -cos(t)}} \right.\)Substitute in variables [Arc Length Formula - Parametric]: \(\displaystyle AL = \int\limits^{\pi}_0 {\sqrt{[1 + sin(t)]^2 + [-cos(t)]^2}} \, dx\)[Integrand] Simplify: \(\displaystyle AL = \int\limits^{\pi}_0 {\sqrt{2[sin(x) + 1]} \, dx\)[Integral] Evaluate: \(\displaystyle AL = \int\limits^{\pi}_0 {\sqrt{2[sin(x) + 1]} \, dx = 4\sqrt{2}\)Topic: AP Calculus BC (Calculus I + II)
Unit: Parametric Integration
Book: College Calculus 10e
Do
this mathematics operations using the rules of precision
(9.11)+(6.232)
(7.4023)x(19)
(9.162)-(2.39)
(0.00482)x(213)
(8.73)/(5.198)
(7644)/(0.13)
Answers
Answer:
Step-by-step explanation:
Sure! I'll perform the mathematical operations using the given numbers and apply the rules of precision. Please find the results below:
(9.11) + (6.232)
The sum of 9.11 and 6.232 is 15.342.
(7.4023) x (19)
The product of 7.4023 and 19 is 140.844.
(9.162) - (2.39)
The difference between 9.162 and 2.39 is 6.772.
(0.00482) x (213)
The product of 0.00482 and 213 is 1.02786.
(8.73) / (5.198)
The division of 8.73 by 5.198 is 1.67920734.
(7644) / (0.13)
The division of 7644 by 0.13 is 58,800.
Please note that the results are rounded to the appropriate number of decimal places based on the precision rules.
In which function is x = 2 mapped to 32?
O
f(x)=-3x²-4
g(x) = 4(x+3)²-68
Oh(x) = 3x
Ox)=2x-62
Answers
The function g(x) = 4(x + 3)² - 68 is the function which is mapped to 32 at x = 2 option (B) g(x) = 4(x + 3)² - 68 is correct.
To find the solution, add 2 to the function's x-values and compute the value.
What is a function?
It is described as a particular kind of relationship, and each value in the domain is associated to exactly one value in the range according to the function. They have a predetermined domain and range.
We have:
A function which is at x = 2 mapped to 32
The above statement means that at x = 2
The value of the function will be 32
The given functions:
f(x) = -3x² - 4
Plug x = 2
f(2) = -3(2)² - 4
f(2) = -16
g(x) = 4(x + 3)² - 68
Plug x =2
g(2) = 4(2 + 3)² - 68
g(2) = 100 - 68
g(2) = 32
Thus, the function g(x) = 4(x + 3)² - 68 is the function which is mapped to 32 at x = 2 option (B) g(x) = 4(x + 3)² - 68 is correct.
Learn more about the function here:
brainly.com/question/5245372
#SPJ9
Determine mCD
MAB = 88°
m/AED = 80°
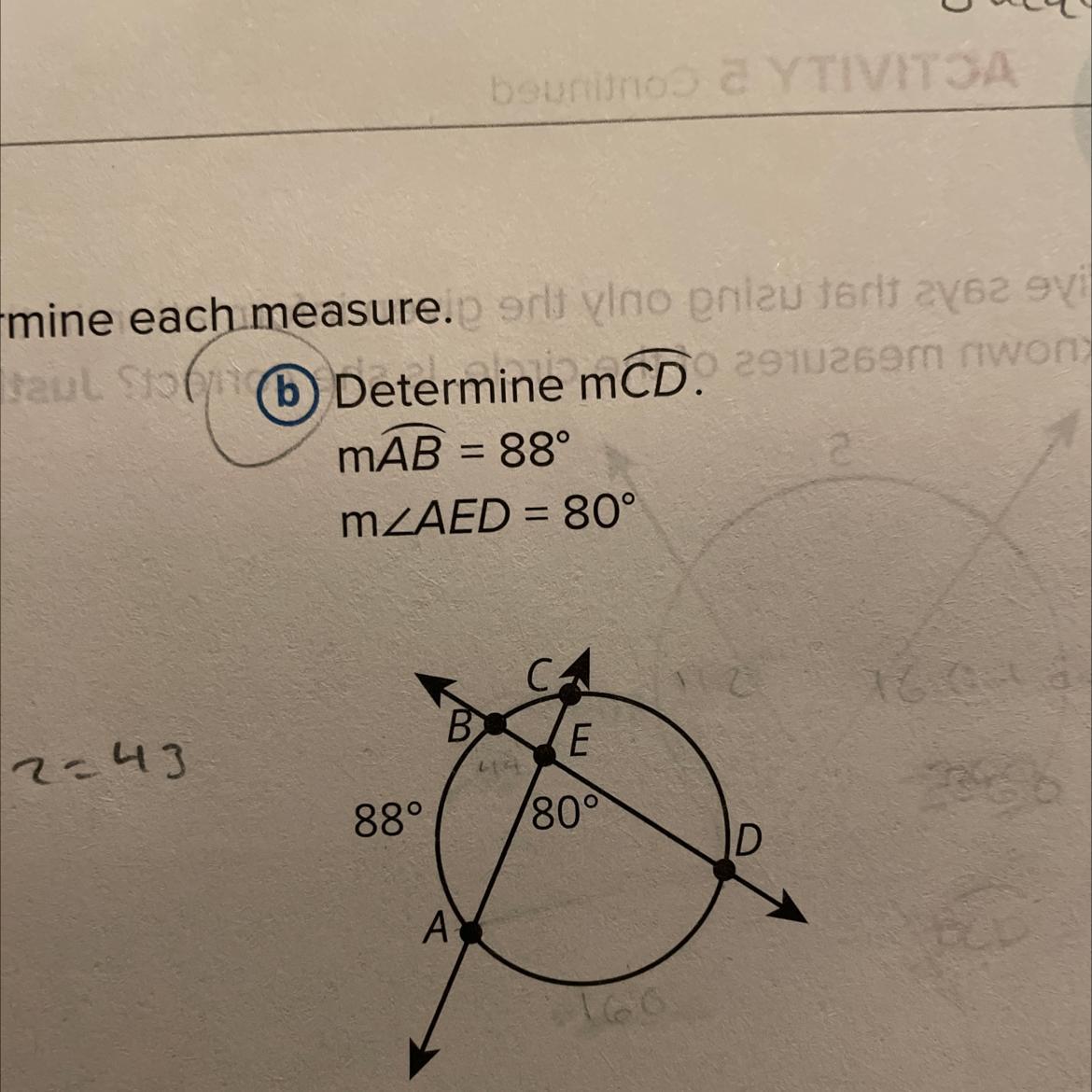
Answers
Answer:
arc CD = 112°
Step-by-step explanation:
the measure of a chord- chord angle is half the sum of the measures of the arcs intercepted by the angle and its vertical angle.
∠ AED and ∠ CED are a linear pair and sum to 180° , that is
80° + ∠ CED = 180°( subtract 80° from both sides )
∠ CED = 100°
then
\(\frac{1}{2}\) (CD + AB) = ∠ CED
\(\frac{1}{2}\) ( CD + 88) = 100° ( multiply both sides by 2 to clear the fraction )
CD + 88° = 200° ( subtract 88° from both sides )
CD = 112°
Consider the following claim:
H0:=0H:≠0H0:rho=0Ha:rho≠0
If n =18 and
=r=
0
compute
⋆=−21−2‾‾‾‾‾‾‾√t⋆=rn−21−r2
Answers
The value of t⋆ is −0.98.
The given hypothesis test is a two-tailed test. It is a test of correlation between two variables. In this test, we are testing if the population correlation (ρ) is equal to zero or not. The given values are as follows:
n =18
r =0
We need to compute the value of t⋆ using the given values of r and n.
The formula to calculate the value of t⋆ is given below.⋆=−21−2‾‾‾‾‾‾‾√t⋆=rn−21−r2
Substitute the given values in the formula.
=−21−2‾‾‾‾‾‾‾√⋆=180−21−02
=−21−2‾‾‾‾‾‾‾√⋆=−0.98
Therefore, the value of t⋆ is −0.98.
Learn more about Null Hypothesis: https://brainly.com/question/30821298
#SPJ11
Discuss four applications of the capital asset pricing model (CAPM). (8 marks) Dzikunze Manufacturing Limited is considering to raise an extra Sh.10 million in order to finance an expansion programme. The company's current capital structure is given as follows: Additional information: 1. The company is considering raising the funds using two alternative financing options namely: Option t: To raise all the funds through the issue of new ordinary shares at par. Option II: To raise half of the funds through the issue of new ordinary shares at par and the balance through the issue of new 12% debentures at par. 2. The corporation tax rate is 30 s. Required: (i) Earnings belore interest and tax (FB|T) at the point of indifference in company's earnings for each financing option. (8 marks).
Answers
Capital asset pricing model (CAPM) Applications of Capital Asset Pricing Model (CAPM) are as follows;The most important application of CAPM is in the calculation of the cost of equity.
CAPM is used by financial analysts and investors to determine the appropriate rate of return for individual stocks and portfolios. CAPM is also useful in determining the required rate of return for capital projects. By calculating the cost of equity capital, companies can make better investment decisions by determining which projects will yield the greatest return on investment.
CAPM can be used in the valuation of assets, such as stocks, real estate, and other investments. Finally, CAPM is useful in evaluating risk.
To know more about Capital visit :
https://brainly.com/question/32408251
#SPJ11
which one of the following is a type of face found on a platonic solid. A,regular hexagon, B. regular octagon, C.regular nonagon, D. regular pentagon
PLEASE NEED OF AN ANSWER
Answers
Answer:
B. regular octagon
I hope this will help you
Damian dove into a swimming pool from that side. He dove 5 feet down under the water. Then, He swam back to the surface. Write a integer (positive or negative number) that represents where he is now
Answers
The integer that represents where he is now is -5.
What is the whole number?
Whole numbers are numbers without fractions and it is a collection of positive integers and zeros. It is represented by the symbol “W” and the set of numbers is {0, 1, 2, 3, 4, 5, 6, 7, 8, 9,……………}.
After diving 5 feet down into the swimming pool, Damian is at a depth of -5 feet, because he is underwater and the number is negative.
An integer is a positive or negative whole number, such as -5.
The negative sign denotes that Damian is underwater and the 5 is the distance he dove below the surface.
Hence, the integer that represents where he is now is -5.
To learn more about the whole number visit,
https://brainly.com/question/29263205
#SPJ1
1- In Euclidean space, the locus of points equidistant from the origin of a plane is a circle What is the locus of points equidistant (in the spacetime distance seme) from the origin of a spacetime plane? 151 2. A ruler of length L. In at rest in with its left and at the origin. O moves from left to right with speed relative to o along the length of the ruler. The two origins coincide ut time zero for both, at which time a photon is emitted toward the other end of the rulut. What are the coordinates in Olof the event at which the photon maches the other end? (10) 3. The Earth and Alpha Centauri are 43 light years apart. Ignore their relative motion Events A and B occur att on Earth and at 1 year on Alpha Centauri, respectively. (a) What is the time difference between the events according to an observer moving at B - 0.98 from Earth to Alpha Centauri? (b) What is the time difference between the events according to an observer moving at 3 = 0.98 from Alpha Centauri to Earth? (c) What is the speed of a spacecraft that makes the trip from Alpha Centauri to Earth in 2.5 years according to the spacecraft clocks? (d) What is the trip time in the Earth rest frame? [5+5+5+51 + Plane polar coordinates are related to cartesian coordinates by x=rcos and y = rsin. Describe the transformation matrix that maps cartesian coordinates to polar coordinates, and write down the polar coordinate basis vectors in terms of the basis vectors of cartesian coordinates. [51 5- suppose that we are given a basis ei, es consisting of a pair of vectors making a 45° angle with one another, such that ei hus length 2 and ez has length 1. Find the dual basis vectors for the case of covariant components of the vectors. [101
Answers
1. In the context of spacetime, the locus of points equidistant from the origin of a spacetime plane is a hyperbola.
In Euclidean space, the distance between two points is given by the Pythagorean theorem, which only considers spatial dimensions. However, in spacetime, the concept of distance is extended to include both spatial and temporal components. The spacetime distance, also known as the interval, is given by the Minkowski metric:
ds^2 = -c^2*dt^2 + dx^2 + dy^2 + dz^2,
where c is the speed of light, dt represents the temporal component, and dx, dy, dz represent the spatial components.
To determine the locus of points equidistant from the origin, we need to find the set of points where the spacetime interval from the origin is constant. Setting ds^2 equal to a constant value, say k^2, we have:
-c^2*dt^2 + dx^2 + dy^2 + dz^2 = k^2.
If we focus on a spacetime plane where dy = dz = 0, the equation simplifies to:
-c^2*dt^2 + dx^2 = k^2.
This equation represents a hyperbola in the spacetime plane. It differs from a circle in Euclidean space due to the presence of the negative sign in front of the temporal component, which introduces a difference in the geometry.
Therefore, the locus of points equidistant from the origin in a spacetime plane is a hyperbola.
(Note: The explanation provided assumes a flat spacetime geometry described by the Minkowski metric. In the case of a curved spacetime, such as that described by general relativity, the shape of the locus of equidistant points would be more complex and depend on the specific curvature of spacetime.)
To know more about equidistant, refer here:
https://brainly.com/question/29886221#
#SPJ11
At 24 years of age, Megan is 5 feet, 6 inches tall. The national average for height in women is 5 feet, 4 inches, so Megan is taller than the average woman. The national average is a:
Answers
The national average for height in women is below Megan's height of 5 feet, 6 inches, indicating that Megan is taller than the average woman.
The given information states that Megan is 5 feet, 6 inches tall at the age of 24. It further states that the national average for height in women is 5 feet, 4 inches. By comparing Megan's height with the national average, we can determine that Megan is taller than the average woman.
Since Megan's height of 5 feet, 6 inches exceeds the national average of 5 feet, 4 inches, it is clear that she stands taller than the average woman in the country. This suggests that Megan's height falls above the mean height of women, indicating that she is relatively taller compared to the general female population.
To learn more about average click here
brainly.com/question/30873037
#SPJ11
Help this is overdue

Answers
Answer:
52
--------------
8 | 416
- 40
-----------
16
- 16
-----------
0
If y=sin²x, find the rate at which y changes with respect to x
Please ASAP
Answers
Answer:
The rate of change of y with respect to x can be found by taking the derivative of the function.
If y = sin²x, then dy/dx = 2sinxcosx.
The rate at which y changes with respect to x is 2sinxcosx.
according to the central limit theorem, when n=9, the variance of the distribution of means is:
Answers
According to the central limit theorem, when n=9, the variance of the distribution of means is equal to the population variance divided by the sample size.
Let σ^2 be the population variance. Then, the variance of the distribution of means (also known as the standard error) is σ^2/n.
The central limit theorem states that as the sample size increases, the distribution of sample means approaches a normal distribution with mean μ and variance σ^2/n, where μ is the population mean. Therefore, when n=9, the variance of the distribution of means is σ^2/9.
In summary, when n=9, the variance of the distribution of means is equal to the population variance divided by the sample size, which is σ^2/9.
To know more about variance, visit;
https://brainly.com/question/25639778
#SPJ11
Graph the exponential function
f(x)=2/5)x
Answers
Answer:
Step-by-step explanation:

Kareem heats a beaker of water to a boil. Then he records that the water temperature decreases from 100°C to 19°C in 5 and 2/5 minutes.
What was the change in temperature each minute? Enter your answer in the box.
Answers
Answer:
Step-by-step explanation:
2/5min=24 sec
5 min=300 sec
total=324 seconds
the water decreased 100-19=81 degrees
81/324=0.25 degrees/second
the change in temperature was 0.25 degrees per second
we will multiply by 60
15 degrees per minute
Solve dy/dx=1/3(sin x − xy^2), y(0)=5
Answers
The general solution to the differential equation dy/dx = 1/3(sin x − xy^2), y(0)=5 is: y = ±√[(sin x - e^(x/2)/25)/x], if sin x - xy^2 > 0 and y(0) = 5
To solve this differential equation, we can use separation of variables.
First, we can rearrange the equation to get dy/dx on one side and the rest on the other side:
dy/dx = 1/3(sin x − xy^2)
dy/(sin x - xy^2) = dx/3
Now we can integrate both sides:
∫dy/(sin x - xy^2) = ∫dx/3
To integrate the left side, we can use substitution. Let u = xy^2, then du/dx = y^2 + 2xy(dy/dx). Substituting these expressions into the left side gives:
∫dy/(sin x - xy^2) = ∫du/(sin x - u)
= -1/2∫d(cos x - u/sin x)
= -1/2 ln|sin x - xy^2| + C1
For the right side, we simply integrate with respect to x:
∫dx/3 = x/3 + C2
Putting these together, we get:
-1/2 ln|sin x - xy^2| = x/3 + C
To solve for y, we can exponentiate both sides:
|sin x - xy^2|^-1/2 = e^(2C/3 - x/3)
|sin x - xy^2| = 1/e^(2C/3 - x/3)
Since the absolute value of sin x - xy^2 can be either positive or negative, we need to consider both cases.
Case 1: sin x - xy^2 > 0
In this case, we have:
sin x - xy^2 = 1/e^(2C/3 - x/3)
Solving for y, we get:
y = ±√[(sin x - 1/e^(2C/3 - x/3))/x]
Note that the initial condition y(0) = 5 only applies to the positive square root. We can use this condition to solve for C:
y(0) = √(sin 0 - 1/e^(2C/3)) = √(0 - 1/e^(2C/3)) = 5
Squaring both sides and solving for C, we get:
C = 3/2 ln(1/25)
Putting this value of C back into the expression for y, we get:
y = √[(sin x - e^(x/2)/25)/x]
Case 2: sin x - xy^2 < 0
In this case, we have:
- sin x + xy^2 = 1/e^(2C/3 - x/3)
Solving for y, we get:
y = ±√[(e^(2C/3 - x/3) - sin x)/x]
Again, using the initial condition y(0) = 5 and solving for C, we get:
C = 3/2 ln(1/25) + 2/3 ln(5)
Putting this value of C back into the expression for y, we get:
y = -√[(e^(2/3 ln 5 - x/3) - sin x)/x]
So the general solution to the differential equation dy/dx = 1/3(sin x − xy^2), y(0)=5 is:
y = ±√[(sin x - e^(x/2)/25)/x], if sin x - xy^2 > 0 and y(0) = 5
y = -√[(e^(2/3 ln 5 - x/3) - sin x)/x], if sin x - xy^2 < 0 and y(0) = 5
Note that there is no solution for y when sin x - xy^2 = 0.
Visit here to learn more about differential equation : https://brainly.com/question/14620493
#SPJ11
Please help me solve
Answers
Answer:
I could but can you please put down the problem.
Step-by-step explanation:
Five years ago, someone used her $40,000 saving to make a down payment for a townhouse in RTP. The house is a three-bedroom townhouse and sold for $200,000 when she bought it. After paying down payment, she financed the house by borrowing a 30-year mortgage. Mortgage interest rate is 4.25%. Right after closing, she rent out the house for $1,800 per month. In addition to mortgage payment and rent revenue, she listed the following information so as to figure out investment return: 1. HOA fee is $75 per month and due at end of each year 2. Property tax and insurance together are 3% of house value 3. She has to pay 10% of rent revenue for an agent who manages her renting regularly 4. Her personal income tax rate is 20%. While rent revenue is taxable, the mortgage interest is tax deductible. She has to make the mortgage amortization table to figure out how much interest she paid each year 5. In last five years, the market value of the house has increased by 4.8% per year 6. If she wants to sell the house today, the total transaction cost will be 5% of selling price Given the above information, please calculate the internal rate of return (IRR) of this investment in house
Can you show the math as far as formulas go?
Answers
Given the following information: Five years ago, someone used her $40,000 saving to make a down payment for a townhouse in RTP. The house is a three-bedroom townhouse and sold for $200,000 when she bought it. After paying down payment, she financed the house by borrowing a 30-year mortgage.
Mortgage interest rate is 4.25%. Right after closing, she rent out the house for $1,800 per month. In addition to mortgage payment and rent revenue, she listed the following information so as to figure out investment return: 1. HOA fee is $75 per month and due at end of each year 2. Property tax and insurance together are 3% of house value 3. She has to pay 10% of rent revenue for an agent who manages her renting regularly 4. Her personal income tax rate is 20%. While rent revenue is taxable, the mortgage interest is tax deductible. She has to make the mortgage amortization table to figure out how much interest she paid each year 5. In the last five years, the market value of the house has increased by 4.8% per year 6.
To know more about interest visit:
https://brainly.com/question/30393144
#SPJ11
aahan has a job that guarantees him the same fixed salary increase every year. after 4 years, he makes $56,785; after 9 years, he makes $60,210. what is the equation of the line that would graph his salary over time?
Answers
The equation of line that would graph his salary over time will be;
⇒ y = 1/685x - 38.89
What is Equation of line?The equation of line in point-slope form passing through the points
(x₁ , y₁) and (x₂, y₂) with slope m is defined as;
⇒ y - y₁ = m (x - x₁)
Where, m = (y₂ - y₁) / (x₂ - x₁)
Given that;
After 4 years, he makes $56,785; after 9 years, he makes $60,210.
Now,
Since, After 4 years, he makes $56,785; after 9 years, he makes $60,210.
Hence, The equation of line passes through the points (56,785, 4) and
(60,210, 9).
So, We need to find the slope of the line.
Hence, Slope of the line is,
m = (y₂ - y₁) / (x₂ - x₁)
m = (9 - 4) / (60210 - 56785)
m = 5 / 3425
m = 1/685
Thus, The equation of line with slope 1/685 is,
⇒ y - 4 = 1/685 (x - 56,785)
⇒ y - 4 = 1/685x - 42.89
⇒ y = 1/685x - 42.89 + 4
⇒ y = 1/685x - 38.89
Therefore, The equation of line that would graph his salary over time will be;
⇒ y = 1/685x - 38.89
Learn more about the equation of line visit:
https://brainly.com/question/18831322
#SPJ1
Please help I need it fast

Answers
Answer:
J
Step-by-step explanation:
-11=4(-3)+1
-3 =4(-1)+1
1 =4(0)+1
9 =4(2)+1
13=4(3)+1
21=4(5)+1
R^2-59R-82r^2+60 is equivalent to
Answers
Answer: 83r^2 - 59 + 60
Step-by-step explanation:
R^2 - 59R - 82r^2 + 60
= 83r^2 - 59 + 60