Which of the following combinations of side lengths will form a triangle with vertices X, Y, and Z?
A. XY = 19 mm, YZ = 11 mm, XZ = 29 mm
В. XY = 19 mm, YZ = 11 mm, XZ = 31 mm
C. XY = 19 mm, YZ = 10 mm, XZ = 30 mm
D. XY = 20 mm, YZ = 11 mm, XZ = 32 mm
Answers
It should be C I’m not 100% shor tho
Related Questions
IT WUU Tate for school on a
Given that 35.5% of them were men, 40% of them were women and the rest were
OXFORD
particular day, find the number of students who were punctual for school.
1800 people attended the National Day dinner in a certain constituency.
children, find the number of children who attended the dinner.
Answers
Answer:
Number of students = 441 Students
Step-by-step explanation:
Given:
Percent of women = 40%
Percent of women = 35.5%
Total number of people = 1,800
Find:
Number of students
Computation:
Percent of student = 100% - 35.5% - 40%
Percent of student = 24.5%
Number of students = 1,800 x Percent of student
Number of students = 1,800 x 24.5%
Number of students = 441 Students
need help i dont understand

Answers
Answer:
Step-by-step explanation:
it would be "c" because the question asks for the number that makes the inequality true
4x≤ x+3
the graph in c is saying that every number that is 1 or less than 1 makes the inequality true. so lets take -7 as an example
4 x -7=-28
-28+3=-25
-25 is greater than -28 so the inequality is true. the reason why graph d doesnt work is because if we plug in 2 into the equation, then 4x =8 and x+3=5
5 is not greater than 8 so it doesnt work
What is the range of the function shown on the graph

Answers
Answer:
-2<=y<=-7
Step-by-step explanation:
A man is in a boat 2 miles from the nearest point on the coast. He is to go to point Q, located 3 miles down the coast and 1 mile inland (see figure). He can row at a rate of 4 miles per hour and walk at 4 miles per hour. Toward what point on the coast should he row in order to reach point Q in the least time?
Answers
Answer:
The answer is "0.45385".
Step-by-step explanation:
The time is taken to reach the coast \(= \frac{\sqrt{(2^2 + x^2)}}{4}\)
The time is taken to reach Q after reaching the coast \(= \frac{\sqrt{(1 + (3-x)^2)}}{4}\)
Total time, \(T= \frac{\sqrt{(1 + (3-x)^2)}}{4}+ \frac{\sqrt{(1 + (3-x)^2)}}{4}\)
This has to be minimum,
\(\to \frac{dt}{dx} = 0\)
\(\to \frac{\sqrt{(2^2 + x^2)}}{2} + \frac{\sqrt{1 + (3-x)^2}}{3}\\\\ \frac{x}{4}\sqrt{(4+x^2)} + \frac{(x-3)}{(4\sqrt{(x^2-6x+10)}} = 0\\\\\frac{x^2}{16} \times (4+x^2) = \frac{(x-3)^2}{16 \times (x^2-6x+10)}\\\\x^2(4+x^2) = \frac{(x-3)^2}{(x^2-6x+10)}\\\\4x^2+x^4 = \frac{ x^2+9-6x}{(x^2-6x+10)}\\\\ 4x^2+x^4(x^2-6x+10) = x^2+9-6x\\\\4x^4-24x^3+40x^2+x^6-6x^5+10x^4= x^2+9-6x\\\\x^6-6x^5+ 14x^4-24x^3+39x^2+6x-9=0\\\\\)
x=0.45385
It took Fred 12 hours to travel over pack ice from one town in the Arctic to another town 360 miles away. During the return journey, it took him 15 hours. Assume the pack ice was drifting at a constant rate, and that Fred’s snowmobile was traveling at a constant speed relative to the pack ice. What was the speed of Fred's snowmobile?
Answers
Please hurry What is the measure of LABD? a:51° b:39° c:49° d: 141°

Answers
Answer: Angle ABD is 39°
Step-by-step explanation:
Angle CBA is 90° (given by "box" on the corner of the right triangle)
Angle CBD is given as 51°
Subtract:
90° - 51° = 39°
A circle has a radius of 4 ft. What is its circumference?
Use 3.14 for I, and do not round your answer. Be sure to include the correct unit in your answer.

Answers
Answer:
C=25.13274 ft
Step-by-step explanation:
Circumference=2*pi*r
C=2*pi*4
C=25.13274 ft
According to the property , which choice is equivalent to the quotient below?3577 35 A.5B.C.D.-5E.25

Answers
Answer:
Option A is the right answer mate...
A right circular cone is intersected by a plane that passes through the cone's
vertex and is parallel to its base, as in the picture below. What is produced
from this intersection?
OA. A pair of intersecting lines
OB. A point
OC. A pair of parallel lines
OD. A parabola
Answers
Answer:
B. A point
Step-by-step explanation:
You want a description of the intersection between a plane and a cone given that the plane is parallel to the base and passes through the vertex of the cone.
VertexThe vertex of a cone is a single point. If a plane passes through that, but does not intersect the base of the cone, it will not intersect anywhere else.
The intersection is one point.
__
Additional comment
Figure f in the attachment illustrates this case.

A dilation is a transformation in which the _____, but not the shape, of a geometric figure is changed.
Answers
no explanation really
like dilation 2x, 2y makes the size bigger but the shapes rhe same
The measure of an angle is nineteen times the measure of its supplementary angle. What is the measure of each angle?
Answers
9514 1404 393
Answer:
171° (angle) and 9° (supplement)
Step-by-step explanation:
If 'a' represents the measure of the angle then ...
a = 19(180 -a) . . . . . the angle is 19 times its supplement
20a = 19(180) . . . . add 19a
a = 19(9) . . . . . . . . divide by 20
a = 171 . . . degrees (the angle)
180-a = 9 . . . degrees (the supplement)
Find the value of x, 6,4, 3x, 4x+1

Answers
Answer:
If two chords intersect in a circle, then the product of the segments of one chord equals the product of the segments of the other chord.
6(3x) = 4(4x + 1)
18x = 16x + 4
2x = 4
x = 2
Here is a number line. -5 -4 Feedback -3 -2 -1 0 1 Write down the inequality shown on the number line. 2 3 4 р Note: Please use the letter p in your answer. Total marks: 2
Answers
The inequality shown on the number line is -3<p<2
What is a inequality?Inequalities are simply created through the connection of two expressions. In this case, it should be noted that the expressions in an inequality are not always equal.
Inequalities implies that the expressions are not equal. Here, they are denoted by the symbols ≥ < > ≤.
Based on the information, the inequality shown on the number line is -3<p<2
Learn more about inequalities on
https://brainly.com/question/24372553
#SPJ1

Create an exponential function that models this situation based on the time in secons in the video.
B(t)= __

Answers
Answer:
B(t) = 2*\(2^{t}\)Step-by-step explanation:
You have all correct choices.
We can use the given values and work out the equation:
B(t) = \(ab^{t}\)B(0) = 2 ⇒ a*b⁰ = 2 ⇒ a = 2B(1) = 4 ⇒ a*b¹ = 4 ⇒ 2b = 4 ⇒ b = 2The function for this situation is:
B(t) = 2*\(2^{t}\)Answer:
2(2)^t
Step-by-step explanation:
PLATO
Simplify 6.5/2 raised to the second power
Answers
6.5/2=__^2
Hope that helps if you haven’t alr gotten it
50 POINTS PLEASE HELP I NEED ANWSER NOW what would the reflection look like

Answers
Answer:
Point C will be at (3,1), Point B will be at (7,1) and Point A will be at (7,5)
Step-by-step explanation:
Find the difference (6x+7)/(2x) - (3)/(x^(2))
Answers
Answer:
\( \frac{(6x + 7)}{(2x)} - \frac{3}{ {x}^{2} } \\ = \frac{x(6x + 7) - 6}{2 {x}^{2} } \\ = \frac{ {6x}^{2} + 7x - 6}{2 {x}^{2} } \\ = 3 + \frac{7}{2x} - \frac{3}{ {x}^{2} } \)
i really need help!!!!!
there are like 5 questions.





Answers
Answer:
3
Step-by-step explanation:
The answer is three because u need to simply the fractions
Inequalities - Introduction

Answers
Answer:
Step-by-step explanation:
This number line says that we can take all values of x that are less than or equal to 2. That is, the solution is
\(x\leq 2\)
NOTE: if the circle at 2 were not filled in then that would mean x<2 (2 would not be an accepted value of x)
( 3/4 ÷ 3/100 −23 1/2 )÷1 1/2 · 2/3 +1 1/6
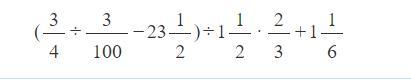
Answers
Answer:
-7333/4400
Step-by-step explanation:
Hope this helps :)
Use a calculator to find the value of the inverse function in radians.see image

Answers
Given:
\(\tan^{-1}(-0.09)\)Sol:
Graph of the inverse of tan(x) is:
So the value is:
\(\tan^{-1}(-0.09)=-0.09\)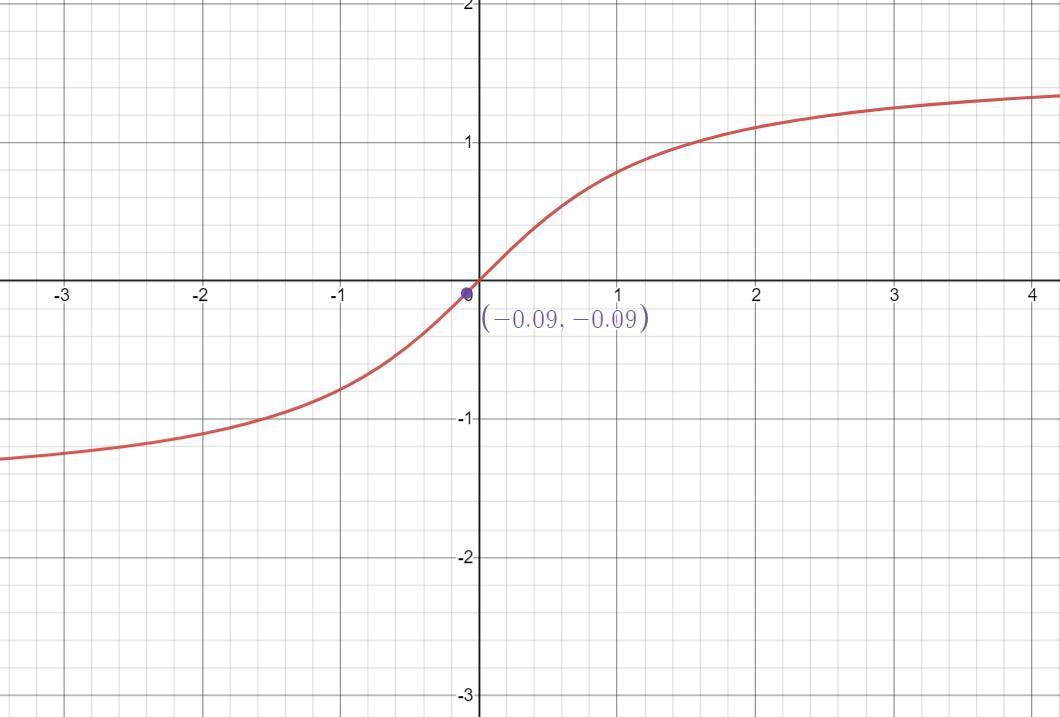
What rule can you come up with if you have to multiply to get a positive number and add to get a negative number?
Answers
Answer:
Two signs
When adding positive numbers, count to the right.
When adding negative numbers, count to the left.
When subtracting positive numbers, count to the left.
When subtracting negative numbers, count to the right.
Step-by-step explanation:
Alberto measures the length of a piece of wire to be 105 cm. The actual length of the wire was 120 cm. What was the percent error of Alberto's measurement? Show your work.
Answers
Answer:
12.5%
Step-by-step explanation:
105 over 120 is the fraction that he got so you subtract 105 from 120 to get how much he missed. 120-105=15
He miscalculated by 15 cm out of the total of 120, 15/ 120
15/120=5/40=2.5/20 multiply the top and bottom by 5 to get the percentage out of 100. 2.5 times 5 =12.5, so he miscalculated by 12.5%
What is the value of the fraction below?
0
26
O A. O
B. Undefined
Answers
Question
From a point P on a level ground and directly west of a pole, the angle of elevation of the top of the pole is 45° and from point Q east of the pole, the angle of elevation of the top of the pole is 58°. If |PQ|= 10m, calculate, correct to 2 significant figures, the:
a) distance from P to the pole;
b) height of the pole.

Answers
a) The distance from point P to the pole is: 6.2 m
b) The height of the Pole is: 6.2 m
How to find the distance and height from angle of elevation?The triangle attached shows us the triangle formed as a result of the given word problem about angle of elevation and distance and height.
Now, we are given that:
The angle of elevation of the top of the pole = 45°
Angle of elevation of the top of the pole = 58°.
|PQ|= 10m
a) PR is distance from point P to the pole and using trigonometric ratios, gives us:
PR/sin 58 = 10/sin(180 - 58 - 45)
PR/sin 58 = 10/sin 77
PR = (10 * sin 58)/sin 77
PR = 8.7 m
b) P O can be calculated with trigonometric ratios as:
P O = PR * cos 45
P O = 8.7 * 0.7071
P O = 6.2 m
Now, the two sides of the isosceles triangle formed are equal and as such:
R O = P O
Thus, height of pole R O = 6.2 m
Read more about distance from angle of elevation at: https://brainly.com/question/25748640
#SPJ1

Find the slope of the tangent line to the curve defined by 4x2+5xy+y4=370
at the point (−9,−1)
Answers
Answer:
The slope of the tangent line to the curve at the given point is -11/7.
Step-by-step explanation:
Differentiation is an algebraic process that finds the gradient (slope) of a curve. At a point, the gradient of a curve is the same as the gradient of the tangent line to the curve at that point.
Given function:
\(4x^2+5xy+y^4=370\)
To differentiate an equation that contains a mixture of x and y terms, use implicit differentiation.
Begin by placing d/dx in front of each term of the equation:
\(\dfrac{\text{d}}{\text{d}x}4x^2+\dfrac{\text{d}}{\text{d}x}5xy+\dfrac{\text{d}}{\text{d}x}y^4=\dfrac{\text{d}}{\text{d}x}370\)
Differentiate the terms in x only (and constant terms):
\(\implies 8x+\dfrac{\text{d}}{\text{d}x}5xy+\dfrac{\text{d}}{\text{d}x}y^4=0\)
Use the chain rule to differentiate terms in y only. In practice, this means differentiate with respect to y, and place dy/dx at the end:
\(\implies 8x+\dfrac{\text{d}}{\text{d}x}5xy+4y^3\dfrac{\text{d}y}{\text{d}x}=0\)
Use the product rule to differentiate terms in both x and y.
\(\boxed{\dfrac{\text{d}}{\text{d}x}u(x)v(y)=u(x)\dfrac{\text{d}}{\text{d}x}v(y)+v(y)\dfrac{\text{d}}{\text{d}x}u(x)}\)
\(\implies 8x+\left(5x\dfrac{\text{d}}{\text{d}x}y+y\dfrac{\text{d}}{\text{d}x}5x\right)+4y^3\dfrac{\text{d}y}{\text{d}x}=0\)
\(\implies 8x+5x\dfrac{\text{d}y}{\text{d}x}+5y+4y^3\dfrac{\text{d}y}{\text{d}x}=0\)
Rearrange the resulting equation in x, y and dy/dx to make dy/dx the subject:
\(\implies 5x\dfrac{\text{d}y}{\text{d}x}+4y^3\dfrac{\text{d}y}{\text{d}x}=-8x-5y\)
\(\implies \dfrac{\text{d}y}{\text{d}x}(5x+4y^3)=-8x-5y\)
\(\implies \dfrac{\text{d}y}{\text{d}x}=\dfrac{-8x-5y}{5x+4y^3}\)
To find the slope of the tangent line at the point (-9, -1), substitute x = -9 and y = -1 into the differentiated equation:
\(\implies \dfrac{\text{d}y}{\text{d}x}=\dfrac{-8(-9)-5(-1)}{5(-9)+4(-1)^3}\)
\(\implies \dfrac{\text{d}y}{\text{d}x}=\dfrac{72+5}{-45-4}\)
\(\implies \dfrac{\text{d}y}{\text{d}x}=-\dfrac{77}{49}\)
\(\implies \dfrac{\text{d}y}{\text{d}x}=-\dfrac{11}{7}\)
Therefore, slope of the tangent line to the curve at the given point is -11/7.
Is r = 6 a solution to the inequality below? 10 < r
Answers
Answer:
No
Step-by-step explanation:
10 is not less than 6, so 10 < r when r=6 is not true.
The average grade for an exam is 74, and the standard deviation is 7. The grades are curved to follow a normal distribution.
What is the probability that the grade of a randomly selected students score is more than 60?
Answers
Answer:
0.9772 = 97.72% probability that the grade of a randomly selected students score is more than 60.
Step-by-step explanation:
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
The average grade for an exam is 74, and the standard deviation is 7.
This means that \(\mu = 74, \sigma = 7\)
What is the probability that the grade of a randomly selected students score is more than 60?
This is 1 subtracted by the pvalue of Z when X = 60. So
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{60 - 74}{7}\)
\(Z = -2\)
\(Z = -2\) has a pvalue of 0.0228
1 - 0.0228 = 0.9772
0.9772 = 97.72% probability that the grade of a randomly selected students score is more than 60.
The mean age of 5 people in a room is 37 years.
A person enters the room.
The mean age is now 34.
What is the age of the person who entered the room?
please help me this is hard for me
Answers
The age of the person who entered the room is 19
How to determine what is the age of the person who entered the room?The given parameters are:
The mean age of 5 people in a room = 37 years.The mean age of now = 34 years.Mean is calculated as:
Mean = Sum/Count
For the five people, we have
Sum/5 = 37
Multiply by 5
Sum = 185
For the five people, we have
Sum/6 = 34
Multiply by 6
Sum = 204
Let the last person be x
So, we have
x + 185 = 204
Subtract 185
x = 19
Hence, the age of the person who entered the room is 19
Read more about mean at:
https://brainly.com/question/20118982
#SPJ1
Is the relation shown in the table below a function? (type in yes or no)

Answers
Answer:
Yes
Step-by-step explanation:
To know if a table is a function or not, we have to see if 1 input only has 1 output.
Looking at the table each input only has 1 output, so it is a function.