Which of the following choices will simplify (2 + 6) . 12.3+19
Answers
Answer:
(2+6=8) and 12.3+19=21.3 hope this helps
Step-by-step explanation:
Related Questions
Use the distributive property to remove the parentheses.
-6(-2x+4w-3)
Answers
Answer:
To remove the parentheses using the distributive property, we need to distribute the -6 to both terms inside the parentheses. This gives us:
(-6)(-2x) + (-6)(4w) + (-6)(-3)
Simplifying this expression using the distributive property gives us:
-12x + (-24w) + 18
Combining like terms, we get:
-12x - 24w + 18
This is the expression with the parentheses removed.
Select the correct answer from each drop-down menu. The inequality 5m − 7 > 16 holds true for all numbers _ than _ in the set {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
Answers
The values of {m} that is greater than 4.6 represent the solution of the given inequality.
An inequality is used to compare two or more expressions or numbers.
For example -
2x > 4y + 3
x + y > 3
x - y < 6
The given inequality is -
5m - 7 > 16
Adding 7 on both sides, we get -
5m - 7 + 7 > 16 + 7
5m > 23
m > 23/5
m > 4.6
Therefore, the values of {m} that is greater than 4.6 represent the solution of the given inequality.
To solve more questions on inequality, visit the link-
brainly.com/question/11897796
#SPJ1
Find the circumference and area of a circle with diameter 6 inches
Answers
Given a circle with d = 6 in.
Circunference:
C = π × d
C = π × 6 in
C = 18.85 in
Area:
A = π × r²
A = π × 3²
A = 28.27 in²
ANSWER
circumference = 18.85 in
area = 28.27 in²
The difference of Mary's age (y) and her older brother's age (x) is 2.
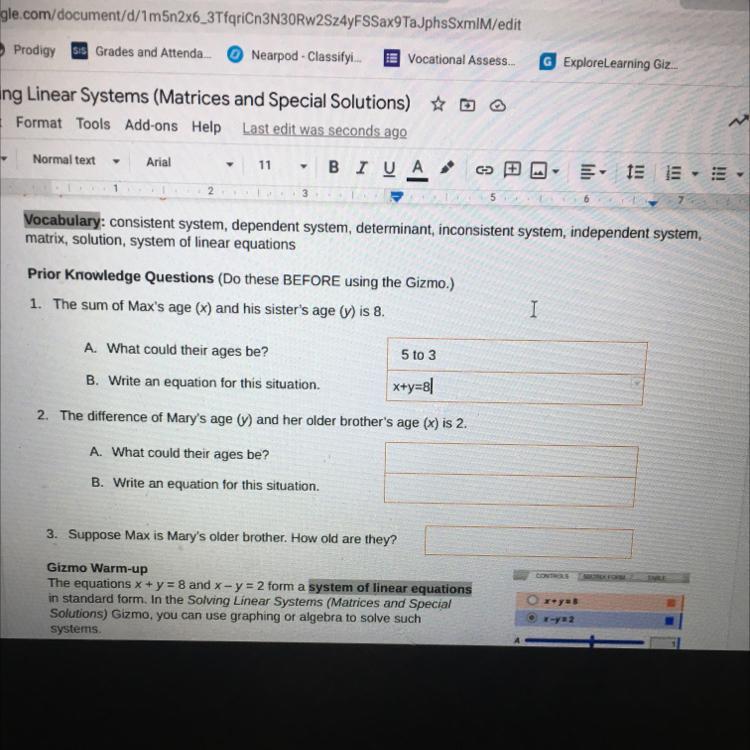
Answers
Possible age:
older brother could be 10
mary could be 8
Equation:
x - y = 2
one card is drawn from a pack of 52cards each of the 52 cards being equally likely to be drawn. what is the probability that the card drawn is a king?
Answers
The probability of drawing a king from a standard deck of 52 cards is 1/13.
In a standard deck of 52 playing cards, there are four kings: the king of hearts, the king of diamonds, the king of clubs, and the king of spades.
To find the probability of drawing a king, we need to determine the ratio of favorable outcomes (drawing a king) to the total number of possible outcomes (drawing any card from the deck).
The total number of possible outcomes is 52 because there are 52 cards in the deck.
The favorable outcomes, in this case, are the four kings.
Therefore, the probability of drawing a king is given by:
Probability = (Number of favorable outcomes) / (Number of possible outcomes)
= 4 / 52
= 1 / 13
Thus, the probability of drawing a king from a standard deck of 52 cards is 1/13.
This means that out of every 13 cards drawn, on average, one of them will be a king.
It is important to note that the probability of drawing a king remains the same regardless of any previous cards that have been drawn or any other factors.
Each draw is independent, and the probability of drawing a king is constant.
For similar question on probability.
https://brainly.com/question/7965468
#SPJ8
What is the area of the parallelogram 60ftx67ft-52ft
Answers
To find the area of a parallelogram, you need to multiply the base by the height. In this case, the given dimensions are 60ft (base) and 67ft (height), and you need to subtract 52ft from the height.
New height = 67ft - 52ft = 15ft
Area of the parallelogram = Base * Height = 60ft * 15ft = 900 square feet.
Therefore, the area of the parallelogram is 900 square feet.
~~~Harsha~~~
Which variable expression represents the word phrase?
the sum of 12 and the quotient of 9 and a number
12−(9÷y)
9 + (12 ÷ y)
12 + (9 ÷ y)
12−9y
Answers
Answer:
Answer is 12+(9÷y)
Hope this helps
Can somebody please help with this? I've been stuck on it for a while

Answers
The reason why is because of the proportions to each intersection of linesare equal to each other (each is SIMILAR, like forming a triangle). In this case, they will both end up having the same fraction but in different form.
So, for the smaller set on the right the fraction is 8.5/5, meaning the fraction is width/height.
The same will go for the left one: width/height. This means that the left will be 29/h.
So, the answer is J. 29/h=8.5/5.
Find the volume of the solid of revolution generated when the region in the first quadrant bounded by the graphs of y = x2 +1, y = 5, and the y-axis is revolved about the line x = -3. a. 8πb.12πc. 20π d. 40π
Answers
When the area in the first quadrant bordered by x=0, y=1, x=y4, and y=10 is rotated about the line y=10, the solid's volume is 11π/3
What is meant by volume?Every three-dimensional item takes up space in some way. The volume of this area is what is used to describe it. The area occupied within an object's three-dimensional bounds is referred to as its volume. The object's capacity is another name for it. Volume is a mathematical term that describes how much space in three dimensions is occupied by an object or a closed surface. The measurement of volume is done in cubic units, like m3, cm3, in3, etc.Volume is a measurement of how much room a thing occupies. To put it another way, just as height and width are terms used to describe size, volume is a measurement of the size of an object.We using,
V = π ∫|(f(x) - d) 2 - (g (x) - d) 2|dx Integrating from a to b
For this case, a = 0, b = 1, g(x) = 1, f(x) = x1/4
Simplifying the equation,
V = π∫|(x1/4 - 10) 2 - (1 - 10) 2dx = π∫|x1/2 - 20x1/4 + 100 - 81|dx
= π[(2/3) x 3/2 - 20(4/5) x 5/4 + 19x] evaluated from at 1 and 0
= π|(2/3 -16 +19) = 11π/3
The complete question is?
find the volume of the solid obtained by rotating the region in the first quadrant bounded by x=0, y=1, x=y^4 about the line y=10
To learn more about volume, refer to:
https://brainly.com/question/463363
#SPJ4
Ty bought a new computer for $499. This brand depreciates at a rate of 12% of the original price per year. The value y of Ty's computer, x years after he purchased it, is found using an equation in the form y = mx + b. What is the approximate value of m?
Answers
Answer:
the approximate value of m is -0.12, indicating that the value of Ty's computer decreases by 0.12 (or 12%) each year.
Step-by-step explanation:
o express this depreciation rate as a slope in the equation y = mx + b, we need to determine how much the value changes (the "rise") for each year (the "run").
Since the value decreases by 12% per year, the slope (m) would be -12%. However, we need to express the slope as a decimal, so we divide -12% by 100 to convert it to a decimal:
m = -12% / 100 = -0.12
How many two or three-digit numbers can you make using the digits 1, 7, 8, 5, and 2?
Answers
Answer:
the are so many numbers but here's one of them
Step-by-step explanation:
Since the number is less than 700, it cannot begin with a 7 or an 8.
So the hundreds digit can only be a 2 or a 5.
Now the tens digit can be any digit not occupying the hudreds digit. So there would be 3 possibilities, and there remain two possibilities for the units digit.
Hence, the number of such numbers is 2x3x2 which is 12.
The number of two-digit or three-digit numbers that can be made using the digits 1, 7, 8, 5, and 2 will be 150.
What is a sample?A sample is a group of clearly specified components. The number of items in a finite set is denoted by a curly bracket.
The number of two-digit numbers that can be made using the digits 1, 7, 8, 5, and 2 is calculated as,
⇒ 5 x 5
⇒ 25
The number of three-digit numbers that can be made using the digits 1, 7, 8, 5, and 2 is calculated as,
⇒ 5 x 5 x 3
⇒ 125
The number of two-digit or three-digit numbers that can be made using the digits 1, 7, 8, 5, and 2 is calculated as,
⇒ 125 + 25
⇒ 150
More about the sets link is given below.
https://brainly.com/question/350477
#SPJ2
Choose the correct answer below


Answers
The correct statement is;
False, because x = \(cos^-^1({\frac{-1}{2} )\) is in the interval \(( -\frac{\pi }{2} , \frac{\pi }{2} )\) that is, \(cos^-^1({\frac{-1}{2} )\) = \(\frac{2\pi }{3}\). So all solutions of cos x = -1/2 will be x = 2π/3 + 2nx and x = 4π/3 + 2nx.
Option D
How to determine the statementFrom the information given, we have that;
All solutions are cos x = -1/2 are given by x = 4x/2 + 2πx
There are multiple solutions to the equation cos x = -1/2, and they are denoted by the values x = 2π/3 + 2nx and x = 4π/3 + 2nx
Such that n is an integer.
This is so because the cosine function repeats itself every 2π, or its period. We therefore multiply the general answer by multiples of 2 to obtain all solutions.
The formula x = 4x/2 + 2πx implies that each solution can be reached by x being multiplied by 4/2 and 2πx being added.
Learn more about cosine function at: https://brainly.com/question/29100023
#SPJ1
how to write 4/5 ÷ 2/3 as a multiplication equation
Answers
We get the equation: 4/5 * 3/2
Hope this helps!
Help plz I don’t understand

Answers
There are integers that are not rational
numbers, true or false?
Answers
Answer:
integers are always rational. They don't include decimals
Step-by-step explanation:
Answer:
False
Step-by-step explanation:
All integers are rational numbers, since they can be expressed as a ratio (fraction) with a denominator of 1.
Will someone be able to help me with this math problem, the picture is down below. Please help

Answers
The dilation transformation of the triangle ABC by a scale factor of 3, with the point P as the center of dilation indicates;
Side A'B' will be parallel to side AB
Side A'C' will be parallel to side AC
Side BC will lie on the same line as side BC
What is a dilation transformation?A dilation transformation is one in which the dimensions of a geometric figure are changed but the shape of the figure is preserved.
The possible options, from a similar question on the internet are;
Be parallel to
Be perpendicular to
Lie on the same line as
The location of the point P, which is the center of dilation, and the lines PC and PA of dilation and the scale factor of dilation indicates that we get;
PB' = 3 × PB
PA' = 3 × PA
PC' = 3 × PC
Therefore; The side B'C' will be on the same line as the side BC
The Thales theorem, also known as the triangle proportionality theorem indicates that;
The side A'C' will be parallel to the side AC
The side A'B', will be parallel to the side AB
Learn more on the Thales theorem here: https://brainly.com/question/14417137
#SPJ1
9. (10 points) Find all values of b such that
3x² - 2bx
to nieme
x ≥-3
-3x² + 5x +4bx x < -3
f(x) =
is continuous at x = -3. What type of discontinuity exists at x = -3
when b is not equal to this value(s)? Explain your answer(s).

Answers
In the function given, the type of discontinuity that exists at x = -3 when b is not equal to 11/6 is a jump discontinuity.
What is the value of bFor the function f(x) to be continuous at x = -3, the limit of f(x) as x approaches -3 from both the left and the right must be equal to f(-3). That is:
lim x→-3+ f(x) = f(-3) = lim x→-3- f(x)
Since x < -3 for the second part of the function, we can calculate the left-hand limit as:
lim x→-3- f(x) = -3(-3)² + 5(-3) + 4b(-3) = 9 + (-15) - 12b = -6 - 12b
And the right-hand limit as:
lim x→-3+ f(x) = 3(-3)² - 2b(-3) = 27 + 6b
Therefore, we must have:
-6 - 12b = 27 + 6b
Solving for b, we get:
b = 33/18 = 11/6
So when b = 11/6, the function is continuous at x = -3.
Now let's consider the case where b is not equal to 11/6. In this case, the left-hand limit and right-hand limit are not equal, which means the function has a jump discontinuity at x = -3. The value of the function at x = -3 from the left-hand side is:
f(-3-) = -3(-3)² + 5(-3) + 4b(-3) = 9 - 15 - 12b = -6 - 12b
And the value of the function at x = -3 from the right-hand side is:
f(-3+) = 3(-3)² - 2b(-3) = 27 + 6b
Therefore, the type of discontinuity that exists at x = -3 when b is not equal to 11/6 is a jump discontinuity.
Learn more on continuity of a function here;
https://brainly.com/question/18102431
#SPJ1
anyone know the answer to number 4?

Answers
answer my questions plz
A. The graph of g(x) is 12 units below the graph of f(x).B. The graph of g(x) is 12 units to the right of the graph of f(x).C. The graph of g(x) is 12 units above the graph of (x).D. The graph of g(x) is 12 units to the left of the graph of (x).

Answers
We are given an initial function:
\(f(x)=x^2\)And we are given the function:
\(g(x)=(x-12)^2\)The relationship between the two functions is the following:
\(g(x)=f(x-12)\)When we have this type of relationship:
\(g(x)=f(x-a)\)This means that the graph of g(x) is the translation of "a" units to the right of the graph of f(x).
Therefore, the graph of g(x) is 12 units to the right of the graph of f(x)., The right answer is B
Mrs. Aldridge spilled coffee on her Answer Key and can't see the width of
the rectangle anymore. What would be the width of a rectangle with the
given area (shown in image below)?
x +9
x² + 11x + 18
(My answer is a guess so please show your work if you answer this question!)
thank you:)

Answers
Answer:
x + 2
Step-by-step explanation:
Area = x² + 11x + 18
length = x + 9
width = ?
Area = length x width
Factor the polynomial x² + 11x + 18:
length x width = (x + 9)(x + 2) = x² + 11x + 18
The length is x + 9, therefore the width is x + 2
Math Homework: Unit 3 Assignment

Answers
Match the SLOPE of the line that goes through each pair of points (use the slope formula (y2-yl) / (x2-x1) * 5 undefined 5/2 (4,7) and (6,2) (-3,5) and (-2,0) Ο Ο Ο Ο (4,7) and (4, 2) Ο Ο Ο Ο Ο Ο (3,6) and (-2, 6) This question requires one response per row
Answers
To find the slope, use the formula below:
\(\text{slope}=\frac{y2-y1}{x2-x1}\)A. (4, 7) and (6, 2)
Here, we have:
(x1, y1) ==> (4, 7)
(x2, y2) ==> (6, 2)
\(\begin{gathered} \text{slope = }\frac{y2-y1}{x2-x1}=\frac{2-7}{6-4}=\frac{-5}{2} \\ \\ \text{slope =-}\frac{5}{2} \end{gathered}\)B. (-3, 5) and (-2, 0)
\(\begin{gathered} \text{slope = }\frac{y2-y1}{x2-x1}=\frac{0-5}{-2-(-3)}=\frac{0-5}{-2+3}=\frac{-5}{1}=-5 \\ \\ \text{slope = -5} \end{gathered}\)C. (4, 7) and (4, 2)
\(\begin{gathered} \text{slope = }\frac{y2-y1}{x2-x1}=\frac{2-7}{4-4}=\text{ }\frac{-5}{0}=\text{ undefined} \\ \\ \text{The slope here is undefined} \end{gathered}\)D. (3, 6) and (-2, 6)
\(\begin{gathered} \text{slope = }\frac{y2-y1}{x2-x1}=\frac{6-6}{-2-3}=\frac{0}{-5}=0 \\ \\ \text{slope = 0} \end{gathered}\)Someone please just help me my grads are so bad please help me out

Answers
Answer:
7 is top answer bottom is 6, 5, and 5
Step-by-step explanation:
simple math but your welcome
A rectangular poster is 50 centimeters long and 25 centimeters wide. If 1 centimeter is approximately 0.4 inches, which of the following best represents the area of the poster in inches?
Answers
The area of the poster in inches is,
⇒ A = 4 inches²
We have to given that;
A rectangular poster is 50 centimeters long and 25 centimeters wide.
Here, 1 centimeter is approximately 0.4 inches
Hence, Lenght = 50 cm
Lenght = 50 x 0.4
= 2 inches
Width = 25 cm
= 25 x 0.4
= 1 inches
Thus, The area of the poster in inches is,
⇒ A = 1 x 4
⇒ A = 4 inches²
Learn more about the rectangle visit:
https://brainly.com/question/2607596
#SPJ1
Find the solution set for the following problem.Two times a number increased by one is at least seven. {xl x>-3) {x| x >-3) {xl x < 3) {x| x > 3]
Answers
Solution
Step 1
Write an expression for the question
Let the number be x
2x + 1 ≥ 7
2x ≥ 7 -1
2x ≥ 6
2x/2 ≥ 6/2
x ≥ 3
Step 2
Write the solution set for the problem
{x | x ≥ 3} Option D
An SUV's gas tank can hold 16 gallons of gas. Suppose the
tank has 8 gallons of gas in it, and the SUV's owner then uses
2 gallons while running errands. How many gallons of gas will he
need to fill up the tank?
Please I need the right answer quick
Answers
Answer:
10
Step-by-step explanation:
the max is 18 it currently has 8 the owner used 2
16- (8-2)
16-6
10
how much would $300 invested at 4% interest compounded monthly be worth after 8 years? round your answer to the nearest cent
Answers
Answer:
412.92
Step-by-step explanation:
\(A = P(1+\frac{r}{n} )^{nt}\)
A: Amount, P: Principal, r: interest, n: no.of times compounded yearly and t: time in years
We have P = 300
r = 4% = 0.04
n = 12 (compounded monthly)
t = 8
\(A = 300(1+\frac{0.04}{12} )^{12*8}\\\\300(\frac{12.04}{12} )^{96}\\\\= 412.92\)
*Urgent*I beeen working on this assignment for 2 hours so if uur good with these stay with me and help please/ Also answer this

Answers
Answer:
17x and (5x+2) + (7x+ 3)
Step-by-step explanation:
A right triangle has one leg 3 meters long and a hypotenuse 5 meters long. What is the length of the other leg? A. 4 m B. 5 m C. 15 m D. 25 m
Answers
Answer:
A
Step-by-step explanation:
Using the Pythagorean Theorem, you can find that the length of the final leg is:
\(\sqrt{5^2-3^2}=\sqrt{25-9}=\sqrt{16}=4\)
Therefore, the answer is A. Hope this helps!
A cistern in the form of an inverted circular cone is being filled with water at the rate of 55 liters per minute. If the cistern is 7 meters deep, and the radius of its opening is 5 meters, find the rate at which the water level is rising in the cistern 20 minutes after the filling process began. Round any intermediate calculations, if needed, to no less than six decimal places, and round your final answer to three decimal places. (Hint: 1m^3=1000L.)
Answers
The rate at which the water level is rising in the cistern 20 minutes after the filling process began 0.0852 meters per minute.
Given that, a cistern in the form of an inverted circular cone is being filled with water at the rate of 55 liters per minute.
What is the volume of a cone?The volume of a cone is the amount of space occupied by a cone in a three-dimensional plane. A cone has a circular base, which means the base is made of a radius and diameter. The volume of a cone formula is 1/3 πr²h.
We are given that the cistern is 7 meters deep and 5 meters for the opening, such that we can relate it to the radius, r, and the height of the water, h, in it as
7/5 = h/2r
⇒ r=7/5·2/h
⇒ r=14h/5
Now, we can express the volume of the water, V, in the cistern by multiplying the rate at which water is being pumped, R, to the time, t, or
V=Rt
Now, 1/3 πr²h
= 1/3 π(14h/5)²h
= 1/3 π×(196h²)/25 ×h
= π196h³/75
So, Rt=π196h³/75
h³=75Rt/π196
=∛(75Rt/π196)
=∛(75R/π196)·\(t^{(\frac{1}{3})\)
=∛(75R/π196)·1/3 \(t^{(\frac{-2}{3})\)
=1/3 ∛(75R/π196)· \(t^{(\frac{-2}{3})\)
=1/3 ∛(75×55/π196)· \(20^{(\frac{-2}{3})\)
= 1/3× ∛(4125/615.44) 0.1357
= 1/3× 1.885440× 0.1357
= 0.0852 meters per minute
Therefore, the rate at which the water level is rising in the cistern 20 minutes after the filling process began 0.0852 meters per minute.
To learn more about the volume of a cone visit:
https://brainly.com/question/1984638.
#SPJ1