which number is larger 0.707 or 0.71?
Answers
Related Questions
A grounds committee of a housing community plans to build a basketball court in an empty rectangular field
Answers
The mathematical equation f(w) = w² - 6w provides a representation of the remaining surface area, measured in square meters, of the field following the construction of the basketball court.
The rectangular field has an area of length x width, which can be expressed as (2w)(w) = 2w² square meters.
The basketball court has an area of length x width, which can be expressed as (w)(w+6) = w² + 6w square meters.
To find the remaining area of the field after the basketball court is built, we need to subtract the area of the basketball court from the area of the rectangular field.
So the function f(w) representing the remaining area, in square meters, is:
f(w) = 2w² - (w² + 6w)
f(w) = 2w² - w² - 6w
f(w) = w² - 6w
Therefore, the function f(w) = w² - 6w represents the area, in square meters, remaining of the field once the basketball court is built.
Learn more about rectangles here: brainly.com/question/29123947
#SPJ4
Complete question:
A grounds committee of a housing community plans to build a basketball court in an empty rectangular field.
1. The rectangular field-has a width of 2w meters and a length that is 13 meters longer than its width.
2. The basketball court has a width of w meters and a length that is 6 meters longer than its width.
Which function, f(w), represents the area, in square meters, remaining of the field once the basketball court is built?
simplify and find the absolute value

Answers
Step-by-step explanation:
Explanation is in the attachmenthope it is helpful to you

Step-by-step explanation:
{(-10)-(-15)÷5}
-10+15÷5
-10+3
= -7
Which is the last sentence of the proof? because f + e = 1, a2 + b2 = c2. Because f + e = c, a2 + b2 = c2. Because a2 + b2 = c2, f + e = c. Because a2 + b2 = c2, f + e = 1.
Answers
The latest sentence of proof by using the triangle congruence method we can conclude that f+e=c, \(a^{2} + b^{2} = c^{2}\).
Given that ΔABC and ΔCBD are right triangles
Therefore, one angle of both triangle is of 90°
So, ∠B is same in both triangles. Hence, by suing the Angle-Angle theorem rule we can conclude that both ΔABC and ΔCBD are similar.
Consequently, ∠A is same in both triangles. Hence, by suing the Angle-Angle theorem rule we can conclude that both ΔABC and ΔCBD are similar.
Similarly, When two triangles are similar then their corresponding angles are equal and their corresponding sides are also equal.
Therefore , the two proportions can be rewritten as
a² = cf ( equation 1 )
b² = ce ( equation 2 )
By adding b² on both side of equation 1 then we can write equation 1 as
\(a^{2} + b^{2} = b^{2}+cf\)
\(a^{2} + b^{2} = ce+cf\)
Because b² and ce are equal and substitute on the right side of equation 1
Using the converse of distributive property in above equation then we get a new equation. That is,
\(a^{2} +b^{2} = c(f+e)\)
Because distributive property is a(b+c)=a(b+ac)
a² + b² = c²
Because e + f = c²
To learn more about triangle congruency: https://brainly.com/question/1675117
#SPJ4
Find the direction angle of w=8j.
Round your answer to the nearest tenth of a degree
Answers
the direction angle of w=8j is 90.0 degrees. The direction angle of a complex number is the angle between the positive real axis and the vector representing the complex number in the complex plane.
what is direction angle ?
The direction angle, also known as the argument or phase angle, of a complex number is the angle between the positive real axis and the vector representing the complex number in the complex plane.
In the given question,
The direction angle of a complex number is the angle between the positive real axis and the vector representing the complex number in the complex plane.
In this case, the complex number is w=8j, which has an imaginary part of 8 and a real part of 0. Therefore, the vector representing w points directly upwards in the complex plane, and the angle between this vector and the positive real axis is 90 degrees.
Rounding this to the nearest tenth of a degree gives 90.0 degrees.
So the direction angle of w=8j is 90.0 degrees.
To know more about direction angle, visit:
https://brainly.com/question/28522105
#SPJ1
In a study of cell phone usage and brain hemispheric dominance, an internet survey was e-mailed to subjects randomly selected from an online group involved with ears. There were surveys returned. Use a 0. 01 significance level to test the claim that the return rate is less than 20%. Use the p-value method and use the normal distribution as an approximation to the binomial distribution.
Answers
The value of z statistics is -1.878,
Given,
In the question:
Number of random sample selected, n = 6967
Number of surveys returned, x = 1331
Now, According to the question:
Estimated proportion of return rate;
To find the value of p = 1331/6967 = 0.192
Significance level, ∝ = 0.01
z would represent the statistic
We investigate the assertion that the return rate is less than 20%, and the following hypotheses are tested:
Null hypothesis, p₀ ≥ 0.2
Alternative hypothesis, p₀ < 0.2
The statistics, z = (p - p₀) / √(p₀(1 - p₀)/n)
z = (0.191 - 0.2) / √(0.2(1 - 0.2)/6967) = -1.878
Using the alternative hypothesis and the following probability, we can now get the p value:
p value = p(z < - 1.878) = 0.0302
We fail to reject the null hypothesis when the p value exceeds the significance level of 0.01 and there is insufficient evidence to support the conclusion that the return rate is less than 20% at 1% of significance.
Learn more about Hypothesis at:
https://brainly.com/question/13651962
#SPJ4
The first side of a triangle is 4m shorter than the second side. The third side 3 times as long as the first side. The perimeter is 24m. Find the length of each side
Answers
Answer:
1st side= 4m
2nd side= 8m
3rd side= 12m
Step-by-step explanation:
Let the first, second and third side of the triangle be a, b and c meters respectively.
a= b -4 -----(1)
c= 3a -----(2)
Perimeter of triangle
= a +b +c
= 24
a +b +c= 24 -----(3)
From (1): b= a +4 -----(4)
Subst. (2) and (4) into (3):
a +(a +4) +3a= 24
3a +a +a +4= 24
5a +4= 24
5a= 24 -4
5a= 20
Divide both sides by 5:
a= 20 ÷5
a= 4
Substitute a= 4 into (4):
b= 4 +4
b= 8
Substitute a= 4 into (2):
c= 3(4)
c= 12
Thus, the lengths of the first, second, and third side of the triangle are 4m, 8m and 12m respectively.
Astronomers often measure large distances using astronomical units (AU) where 1 AU is the average distance from Earth to the Sun. In the image, represents the distance from a star to the Sun. Using a technique called “stellar parallax,” astronomers determined θ is 0.00001389 degrees.
How far away is the star from the Sun in astronomical units?Show your reasoning.
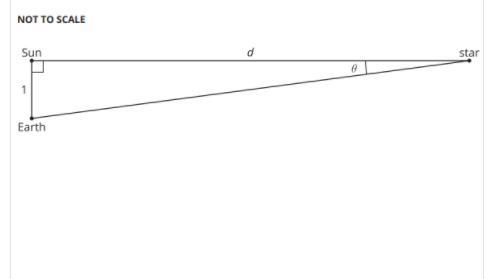
Answers
Answer:
4125000Au
Step-by-step explanation:
my teacher just went over this for our test
The distance between the star and the sun is 4124966.128 AU and this can be determined by using the trigonometric function.
Given :
Astronomers often measure large distances using astronomical units (AU) where 1 AU is the average distance from Earth to the Sun. The image, represents the distance from a star to the Sun. Using a technique called “stellar parallax,” astronomers determined θ is 0.00001389 degrees.The following steps can be used in order to determine the distance between the star and the Sun in astronomical units:
Step 1 - The trigonometric function can be used in order to determine the distance between the star and the Sun in astronomical units.
Step 2 - The sine function can be used to determine the distance.
\(\rm sin\theta=\dfrac{P}{H}\)
where P is the perpendicular and H is the Hypotenuse.
Step 3 - Substitute the known terms in the above expression.
\(\rm sin(0.00001389)=\dfrac{1}{d}\)
Step 4 - Simplify the above expression.
d = 4124966.128
For more information, refer to the link given below:
https://brainly.com/question/21286835
Evaluate each expression if a = 6, b=3, and c= 2.
1. C+4
18
5
2. a-b
3.
2.
a
3
4. b=3
6
5. a-1
8
6. 20
3
7. ab
8. 6+ c
4
Answers
Answer:
b
Step-by-step explanation:
eachone got to go there minus 6
Can somebody please helppppp !

Answers
Match each positive or negative value with the situation that describes it

Answers
Answer:
1.) -10
2.) 10
3.) -27
4.) 27
5.) -8
6.) 8
after fitting a linear regression model to a dataset, the model's slope and intercept are -3 and 0 respectively. now, if we change our independent variable by adding 4.5 units to x, what is the absolute value of the change in the predicted value of dependent variable y?
Answers
The absolute value of change in the predicted value of dependent variable Y is 18.
Any variable whose value is influenced by an independent variable is said to be dependent. The thing that is measured or assessed in an experiment or mathematical equation is the dependent variable. The phrase "the outcome variable" is another name for the dependent variable.
Slope = b = -4
Intercept = a = -2.8
So, the equation of the regression line is
y = a + bx
y = -2.8 - 4x ...Equation 1
Now suppose the value of x is changed by adding 4.5
i.e. put x = x + 4.5
So,
y = -2.8 - 4(x + 4.5)
y = -2.8 -4x - 18 ...Equation 2
Comparing 1 and 2 ,
We get the predicted value of dependent variable Y as 18
Therefore The absolute value of change in the predicted value of dependent variable Y is 18
To learn more about dependent variables visit
https://brainly.com/question/1479694
#SPJ4
30 POINTS FOR AN EXPLANATION TOO (DETAILED PLS)

Answers
The value of x based on the equation given as 3(4x + 6) = 9x + 12 is -2.
How to illustrate the equation?It should be noted that an equation shows that relationship between the variables that are given or illustrated in the data.
The value for x based on the equation will be:
3(4x + 6) = 9x + 12
Open bracket
12x + 18 = 9x + 12
Collect like terms
12x - 9x = 12 - 18
3x = -6
Divide
x = -6/3
x = -2
Therefore, x is -2.
Learn more about equations on:
brainly.com/question/13763238
#SPJ1
Write $a^4 - 3a^2 + 9$ as a product of two monic quadratics with integer coefficients.
Answers
$a^4 - 3a^2 + 9$ can be factorised as $(a^2 - 3)(a^2 + 3)$
To factor $a^4 - 3a^2 + 9$ as a product of two monic quadratics with integer coefficients, we can use the difference of squares factorization.
When an expression has the general form a²+2ab+b², then we can factor it as (a+b)². For example, x²+10x+25 can be factored as (x+5)². This method is based on the pattern (a+b)²=a²+2ab+b², which can be verified by expanding the parentheses in (a+b)(a+b).
$a^4 - 3a^2 + 9$ can be factored as $(a^2 - 3)(a^2 + 3)$
Notice that both factors are monic quadratics with integer coefficients.
So, $a^4 - 3a^2 + 9$ = $(a^2 - 3)(a^2 + 3)$
To learn more about quadratic equations visit: brainly.com/question/22364785
#SPJ4
consider the hypotheses in a hypothesis test. is an alternative hypothesis a statement about a parameter or a statistic? group of answer choices not enough information is given statistic could be either, depending on the context parameter
Answers
The hypothesis in a hypothesis test is an alternative hypothesis a statement about a parameter.
An alternative hypothesis in a hypothesis test is a statement about a parameter, not a statistic. The null hypothesis is typically a statement about a parameter that assumes there is no significant difference or relationship, while the alternative hypothesis is a statement that contradicts the null hypothesis and suggests there is a significant difference or relationship.
The alternative hypothesis can take one of three forms: it can be a one-tailed hypothesis (either greater than or less than the null hypothesis), or a two-tailed hypothesis (not equal to the null hypothesis). In all cases, the alternative hypothesis is a statement about the population parameter, which is typically denoted by a Greek letter such as μ (mean) or σ (standard deviation).
Therefore, the alternative hypothesis is a statement about the parameter being tested.
To learn more about hypothesis tests: https://brainly.com/question/4232174
#SPJ11
In ADEF, the measure of
measure of ZD to the nearest degree.
E
52
X
F
D
14
Answers
Answer:
74 degrees
Step-by-step explanation:
Assuming we have the following
FD = 14
DE = 52
m<F = 90degrees
Required
m<D
DE = hypotenuse
FD = adjacent
Using the SOH CAH TOA identity
Cos m<D = adj/hyp
Cos m<D = 14/52
m<D = arccos(0.2692)
m<D = 74.38
m<D to the nearest degree is 74degrees
A biologist has an 8535-gram sample of a radioactive substance. Find the mass of the sample after four hours if it decreases according to a continuous exponential decay model, at a relative rate of 13% per hour. Do not round any intermediate computations, and round your answer to the nearest tenth. grams ?
Answers
The mass of the sample after four hours is 6426.5 grams.
Given,
The biologist has an 8535-gram sample of a radioactive substance.
Relative rate of decay = 13% per hour.
Using exponential decay formula :N(t) = N_0*e^(-rt)
Here, N(t) = mass of the sample after t hours = N_0*e^(-rt)
N_0 = initial mass of the sample = 8535 grams
r = relative rate of decay = 13% per hour = 0.13
t = time in hours = 4 hours
We need to find mass of the sample after 4 hours i.e. N(t).
We can use the formula, N(t) = N_0*e^(-rt)
Substituting the given values,
N(t) = 8535*e^(-0.13*4)
≈ 6426.5 grams (rounding off to nearest tenth)
Therefore, the mass of the sample after four hours is 6426.5 grams.
To know more about radioactive visit:
https://brainly.com/question/1770619
#SPJ11
How many four-letter permutations can be formed from the first five letters of the alphabet?
Answers
Answer:
120
Step-by-step explanation:
formula:
\(\frac{n!}{(n-h)!}=\frac{5!}{(5-4)!}=120\)
Triangle ABC is isosceles, and segment AB is congruent to segment AC.  AB equals to 1/2x+1/4  and BC equals to 5/2-x. What is the perimeter
Answers
The perimeter of triangle ABC is 3 cm.
Given:- AB is congruent to segment AC
AB= AC= 1/2x + 1/4
BC= 5/2-x
Perimeter of a triangle = Sum of all sides
= (1/2x + 1/4) + (1/2x + 1/4) + (5/2-x)
= 1/2x +1/2x -x +1/4+1/4+5/2
= 3 cm
Therefore, the perimeter of triangle ABC is 3 cm.
To learn more about perimeter of triangle visit;
https://brainly.com/question/24299023
#SPJ4
How to solve 4x+6y less than or equal to 120
Answers
I need this done by tomorrow 4.

Answers
Evaluate x raise to 3 if x = 9
Answers
Answer:
729
Hope you could understand.
If you have any query, feel free to ask.
The scale on a road map indicates that 2 inches = 30 miles. How many inches would represent 120 miles on this road map?
Answers
Answer:
8 inches = 120 miles
Step-by-step explanation:
If 2 inches is equivalent to 30 miles, then divide 120 by 30 then times the answer by two.
120 / 30 = 4
4 x 2 = 8
8 inches = 120 miles
To check;
30 x 4 = 120
8 / 2 = 4
Hope this helps!!!
Answer:
The answer is 8in.
Step-by-step explanation:
Calculated 120/30
Pleaseeee helppppppp

Answers
Answer:
d = 8t
Step-by-step explanation:
Identify the y-intercept of the quadratic f(x)=4x^2-12x+25
Answers
Answer:
The y-intercepts of the quadratic are (0, 25)
Step-by-step explanation:
Hope I helped, have a good day
Ben owns a townhome valued at $195,000, but still owes $120,000 on the loan. ben has $5,000 in savings and a balance of $1,400 on his credit cards. there is a balance of $20,000 owed on ben’s car which is valued at $38,000. what is ben’s net worth? a. $96,600 b. $97,600 c. $99,400 d. $106,600 please select the best answer from the choices provided a b c d
Answers
Answer:
Choice a : $96,600
Step-by-step explanation:
The net worth of a person is computed as total assets - total liabilities in money terms
Ben's assets are as follows:
Townhome: $195,000
Savings: $5000
Car: $38,000
Total Assets: 195000 + 5000 + 38000 = $238,000
Ben's liabilities
Home Loan: $120,000
Credit Card: $1,400
Car Loan: $20,000
Total Liabilities = 120000 + 1400 + 20000 = $141,400
Net Worth = 238000 - 141400 = $96,600 (Answer is choice a)
Answer:
A
Step-by-step explanation:
Find the maximum value on (0, infinity) for f(x)=7x-2xlnx
Answers
f'(x)>0 for all x>0. Therefore f(x) is strictly increasing on the inverval (0,∞).
How to obtain the maximum value of a function?To find the maximum of a continuous and twice differentiable function f(x), we can firstly differentiate it with respect to x and equating it to 0 will give us critical points.
f(x) = max{0,x} then f(x)=0 if x<0 and f(x)=x if x≥0.
f(x)=7x-2xlnx
When x tends to -∞, f is the constant function zero, therefore limit n tends to infinity f(x) = 0.
When x tends to ∞, f(x)=x and x grows indefinitely. Thus limit n tends to infinity f(x) = infinity.
f is differentiable if x≠0. If x>0, f'(x)=1 (the derivative of f(x) = x and if x<0, f'(0)=0 (the derivative of the constant zero).
In x=0, the right-hand derivative is 1, but the left-hand derivative is 0, hence f'(0) does not exist,
f'(x)>0 for all x>0. Therefore f(x) is strictly increasing on the inverval (0,∞).
Learn more about maxima of a function here:
https://brainly.com/question/13333267
#SPJ4
How do I solve this?

Answers
a)
Values of the given angles ∠A = 123° , ∠B = 123° ,∠C = 57.
Given ,
One angle of the figure as 123°.
Now,
∠C and 123° form linear pair.
So,
∠C + 123° = 180°
∠C = 57°
Now,
∠C and ∠B are pairs of interior angles on same side of transversal, thus they are supplementary.
∠C + ∠B = 180°
Substitute the value of ∠C
53° + ∠B = 180°
∠B = 127°
Now,
∠B and ∠A are vertically opposite angles.
Thus,
∠B = ∠A
So,
∠A = 127° .
Hence,
∠A= 127°
∠B = 127°
∠C = 57°
b)
Values of ∠D = 98°, ∠E = 98°, ∠F = 98° .
Given one angle as 82°
Now,
∠F and 82° form linear pair.
So,
∠F + 82° = 180°
∠F = 98°
Now,
∠D and ∠F are corresponding angles. Thus,
∠D = ∠F
∠D = 98° .
Now,
∠D and ∠E are vertically opposite angles.
Thus,
∠D = ∠E
∠E = 98°.
Hence,
∠D = 98°
∠E = 98°
∠F = 98°
c)
Values of ∠G = 75° and ∠H = 75°
Given one angle as 75° .
∠H and 75° are corresponding angles. Thus,
∠H = 75°
Now,
∠H and ∠G are vertically opposite angles.
So,
∠G = 75° .
Hence,
∠G = 75°
∠H = 75°
To learn more about angles by transversal line,
https://brainly.com/question/11293539
#SPJ1
3. find two unit vectors that are orthogonal to both j 2k and i -2j 3k.
Answers
To find two unit vectors that are orthogonal to both j 2k and i -2j 3k, we can use the cross product and normalization techniques. The two unit vectors that satisfy the condition are (2/3)i + (2/3)j + (1/3)k and (2/3)i - (2/3)j - (1/3)k.
First, we need to calculate the cross product of j 2k and i -2j 3k, which is given by:
j 2k × i -2j 3k = (-6) i -3k - (-4)j -6k = (-6) i + 4j -9k
This cross product vector is orthogonal to both j 2k and i -2j 3k, but it is not a unit vector. To find two unit vectors that are orthogonal to both j 2k and i -2j 3k, we need to normalize this cross product vector. We can do this by dividing the cross product vector by its magnitude:
\(||(-6) i + 4j -9k|| = \sqrt{(-6)^2 + 4^2 + (-9)^2) } = 11\\\)
Therefore, the first unit vector that is orthogonal to both j 2k and i -2j 3k is:
\(u1 = (1/11)(-6)i + (4/11)j - (9/11)k\)
To find the second unit vector, we can take the cross product of the first unit vector and either j 2k or i -2j 3k. Let's take the cross product of u1 and j 2k:
\(u1 × j 2k = (-8/11) i - (6/11)j - (2/11)k\)
This vector is also orthogonal to both j 2k and i -2j 3k, but it is not a unit vector. To find the second unit vector, we need to normalize this vector:
\(||(-8/11) i - (6/11)j - (2/11)k|| = \sqrt{(-8/11)^2 + (-6/11)^2 + (-2/11)^2} \\= 2/3\)
Therefore, the second unit vector that is orthogonal to both j 2k and i -2j 3k is:
\(u2 = (2/3)(-8/11)i - (2/3)(6/11)j - (2/3)(-2/11)k \\ = (2/3)i - (2/3)j - (1/3)k\)
Thus, the two unit vectors that are orthogonal to both j 2k and i -2j 3k are (2/3)i + (2/3)j + (1/3)k and (2/3)i - (2/3)j - (1/3)k.
Learn more about unit vectors here:
https://brainly.com/question/28028700
#SPJ11
You survey the students in your class to find out what kinds of movies they like to watch. The students were given the following choices: Comedy (C), Horror (H), Drama (D), Action (A), Romance (R). The following were the results of your survey: C, C, R, R, D, R, H, H, C, A, A, R, A, A, A, R, R, H, H, H, C, H, A, R, D, D, D, D, H, R a. Make a frequency table for the movie genres.
Answers
Answer:
I'm not sure but I think the awnser is
4 C
8 R
5 D
and 7H
Using the data given in the question, given below is the frequency table for the movie genres liked by the students.
Movie genre Number of students
Action 6
Comedy 4
Horror 7
Drama 5
Romance 8
What is frequency distribution table?A frequency table lists a set of values and how often each one appears. Frequency is the number of times a specific data value occurs in your dataset.
Learn more about frequency table here
https://brainly.com/question/12576014
#SPJ3
Construct a polynomial function with the stated properties. Reduce all fractions to lowest terms.Third-degree, with zeros of -2, - 1, and 3, and passes through the point (2, 7).
Answers
ANSWER
\(f(x)=-\frac{7}{12}x^3+\frac{49}{12}x+\frac{7}{2}\)EXPLANATION
If x1, x2, x3, ..., xn are the zeros of a polynomial P, then the polynomial can be written as the product of the factors,
\(P(x)=(x-x_1)(x-x_2)(x-x_3)\ldots(x-x_n)\)In this problem we have a third-degree polynomial function, so it has 3 zeros and thus 3 factors,
\(f(x)=a(x+2)(x+1)(x-3)\)We have to find a knowing that the function has to pass through point (2, 7). This means that when x = 2, f = 7,
\(f(2)=7\)Replace into the function,
\(7=a(2+2)(2+1)(2-3)\)Solve the parenthesis,
\(7=a(4)(3)(-1)\)Multiply,
\(7=a(-12)\)And solve for a by dividing both sides by -12,
\(\begin{gathered} \frac{7}{-12}=\frac{a(-12)}{-12} \\ a=-\frac{7}{12} \end{gathered}\)Hence, the function is
\(f(x)=-\frac{7}{12}(x+2)(x+1)(x-3)\)Next, we have to multiply the factors to obtain the function in standard form. Multiply the first two,
\(f(x)=-\frac{7}{12}(x\cdot x+2x+1x+2\cdot1)(x-3)\)\(f(x)=-\frac{7}{12}(x^2+3x+2)(x-3)\)Then multiply by the last factor,
\(f(x)=-\frac{7}{12}(x^2\cdot x+3x\cdot x+2\cdot x-3\cdot x^2-3\cdot3x-3\cdot2)\)\(f(x)=-\frac{7}{12}(x^3+3x^2+2x-3x^2-9x-6)\)Add like terms,
\(f(x)=-\frac{7}{12}\lbrack x^3+(3x^2-3x^2)+(2x-9x)-6\rbrack\)\(f(x)=-\frac{7}{12}(x^3-7x-6)\)And finally, distribute the coefficient,
\(f(x)=-\frac{7}{12}x^3+\frac{7}{12}7x+\frac{7}{12}6\)\(f(x)=-\frac{7}{12}x^3+\frac{49}{12}x+\frac{7}{2}\)This is the polynomial function with zeros -2, -1 and 3 that passes through point (2, 7)