which list shows the temperature in order from warmest to coldest in degrees Celsius
help me plsss

Answers
Answer:
Step-by-step explanation:
Answer: 9 degrees Celsius, 0 degrees Celsius, -4 degrees Celsius, -12 degrees Celsius
Step-by-step explanation:
Greatest is from Highest to lowest so from 9,0-4,-12 is the correct order
Related Questions
if f(x) = 245
Find f^-1(x) (the inverse)
Answers
9514 1404 393
Answer:
does not exist
Step-by-step explanation:
The notation f^-1(x) usually refers to the inverse function. That is, if we have the functional relation
y = f(x)
Then the inverse function f^-1(x) will give you ...
x = f^-1(y)
__
In order for an inverse function to exist, the original function must pass the "horizontal line test." That is, any horizontal line can intersect the function's graph in, at most, one point.
Here, the function f(x) = 245 is a horizontal line, so the horizontal line test fails. The horizontal line at y=245 will intersect f(x) in an infinite number of points.
So, f(x) = 245 does not have an inverse function. f^-1(x) does not exist.
_____
Alternate interpretation of the question
Sometimes, an exponent is applied to a function name when the intended operation is application of the exponent to the function value. For example, you may see sin²(x) when the intended meaning is sin(x)². The application of an exponent to the function name could be confused with multiple applications of the function: sin²(x) = sin(sin(x)), as the notation is sometimes used for this purpose, too.
If what you intend by f^-1(x) is really f(x)^-1, then you can say ...
f(x)^-1 = 1/245
A bag contains two pencils , one ruler and five pens . What is the probability of randomly selecting a pen , a ruler and a pencil without replacement
Answers

The probability of randomly selecting a pen, a ruler, and a pencil without replacement from the given bag is 5/168.
We have,
Pencils= 2
Ruler = 1
Pens = 5
Total items in the bag: 2 pencils + 1 ruler + 5 pens = 8 items
Now, the Probability of selecting a pen first
P(pen) = 5/8
and, Probability of selecting a ruler second
P(ruler) = 1/7
and Probability of selecting a pencil last
P(pencil) = 2/6 = 1/3
So, the overall probability is
P(pen, ruler, pencil) = P(pen) x P(ruler) x P(pencil)
= (5/8) x (1/7) x (1/3)
= 5/168
Therefore, the probability of randomly selecting a pen, a ruler, and a pencil without replacement from the given bag is 5/168.
Learn more about Probability here:
https://brainly.com/question/31828911
#SPJ2
(10,-1) (9,4) slope?
Answers
Answer:
-5
Step-by-step explanation:
We can use the slope formula
m = ( y2-y1)/(x2-x1)
= ( 4 - -1)/( 9 - 10)
( 4+1)/( 9-10)
5/ -1
- 5
Are the following figures similar? (1 point)
Yes; the corresponding angles are congruent
No; the corresponding angles are not congruent
yes; the corresponding sides are proportional
no; the corresponding sides are not proportional

Answers
Answer:
yes the corresponding angles are congruent...
it can be wrong
Select the correct answer. emily wants to find the number that appears in the middle of a set of 25 numbers arranged in ascending order, in a spreadsheet. which statistical function will help her do so? a. mode b. rank c. median d. average
Answers
The correct answer is option (C) median.
The median will help Emily to find the number that appears in the middle of the 25 numbers that are arranged in ascending order.
What is the mean, median and mode?The mean, median, and mode are the three most commonly used measures of central tendency for populations that do not have much data, that is, they do not need to be grouped.
The mean, also known as average, is the value obtained by dividing the sum of a cluster of numbers by the number of them.
When arranging the numbers from least to largest, the median sits exactly in the middle of the values that are above. The median is a set that is a value that is in the middle of the other values.
The number that appears most frequently in a set of numbers is called the mode.
So, The median will help Emily to find the number that appears in the middle of the 25 numbers that are arranged in ascending order.
To learn more about central tendency, visit: https://brainly.com/question/28101345
#SPJ4
Gina Miss 12 out of 100 questions on her final what ratio of the question did she get correct?
Answers
Answer:
Step-by-step explanation:
100 - 12 = 88
88:100
22:25
Answer:
88
Step-by-step explanation:
12-100=
88
I hope this helped
which checks of plots would be useful for deciding whether the assumptions for two-way anova are met?
Answers
The populations from which the samples are obtained must be normally distributed.
Sampling is done correctly. Observations for within and between groups must be independent.
The variances among populations must be equal (homoscedastic).
Data are interval or nominal.
Find the quotient
54.871 ÷ 7.48
Answers
Answer:
approximately
7.335695
is a parallelogram. is the midpoint of . and trisect .
Let ⃗⃗⃗⃗⃗ = ⃗ and ⃗⃗⃗⃗⃗ = . Show your work on the diagram as well.

Answers
Answer:
option 6b):) is correct
Isabelle earns $200 a week at a bookstore plus $2 for every magazine she sells. She uses the equation to represent her earnings, where x represents magazine sales and y represents her weekly pay. If she needs to earn $280 next week to pay for her school trip, how many magazines does she need to sell?
Answers
Answer:
40 magazines.
Step-by-step explanation:
$200 pay from the bookstore.$2 every magazine sold.Needs $280 for her school trip.She gets $200 from the book store the week she needs $280 for the school trip. Therefore, she only needs $80 in order to go.
$80 ÷ $2 = 40
40 magazines.
Answer:
40 is the answer..... your welcome
Step-by-step explanation:
use the kkt
Use the method of steepest ascent to approximate the solution to max z = -(x₁ - 3)² - (x₂ - 2)² s. t. (x₁, x₂) E R²
Answers
To approximate the solution and maximize the given objective function we need to find the steepest ascent direction and iteratively update the values of x₁ and x₂ to approach the maximum value of z.
The method of steepest ascent involves finding the direction that leads to the maximum increase in the objective function and updating the values of the decision variables accordingly. In this case, we aim to maximize the objective function z = -(x₁ - 3)² - (x₂ - 2)².
To find the steepest ascent direction, we can take the gradient of the objective function with respect to x₁ and x₂. The gradient represents the direction of the steepest increase in the objective function. In this case, the gradient is given by (∂z/∂x₁, ∂z/∂x₂) = (-2(x₁ - 3), -2(x₂ - 2)).
Starting with initial values for x₁ and x₂, we can update their values iteratively by adding a fraction of the gradient to each variable. The fraction determines the step size or learning rate and should be chosen carefully to ensure convergence to the maximum value of z.
By repeatedly updating the values of x₁ and x₂ in the direction of steepest ascent, we can approach the solution that maximizes the objective function z. The process continues until convergence is achieved or a predefined stopping criterion is met.
Learn more about fraction here:
https://brainly.com/question/10354322
#SPJ11
Select all the values of P that are solutions for this inequality 10p-8>12
Answers
Answer: All values/solutions of P must be greater than 2 to be true to the inequality 10p-8>12
Step-by-step explanation:
When solving inequalities, we treat it like an equation, solving for the variable, in this case, p.
10p - 8 > 12
Lets isolate p
10p - 8 > 12
+8 +8
10p > 20
/10 /10
p > 2
After solving, we now know that all values of P must be greater than 2.
John bow 27 packets of paper plates, costing £52.65, for a dinner party that he was hosting. his wife reminded him that he should have bought 35 packets to cater everyone who was coming. how much would this have cost?
Answers
use the trapezoidal rule and simpson's rule to approximate the value of the definite integral for the given value of n. round your answer to four decimal places and compare the results with the exact value of the definite integral. 5 x x2 4 0 dx, n
Answers
Exact value of the definite integral is 320. Comparing the results: Exact value of the definite integral = 320, Trapezoidal Rule approximation (n = 4) = 340, Simpson's Rule approximation (n = 4) ≈ 246.6667.
What is trapezoid?
A trapezoid is a quadrilateral (a polygon with four sides) that has one pair of parallel sides. The parallel sides are called the bases of the trapezoid, while the non-parallel sides are called the legs.
To approximate the value of the definite integral ∫[0, 4] 5x * x^2 dx using the Trapezoidal Rule and Simpson's Rule, we need to specify the value of n, which represents the number of subintervals.
Let's calculate the approximations using n = 4 for both methods:
Trapezoidal Rule:
Using n = 4, we divide the interval [0, 4] into four subintervals of equal width: h = (4 - 0) / 4 = 1.
The approximated value using the Trapezoidal Rule is given by:
\(T_4 = (h/2) * [f(x_0) + 2f(x_1) + 2f(x_2) + 2f(x_3) + f(x_4)]\)
Plugging in the values:
\(T_4 = (1/2) * [f(0) + 2f(1) + 2f(2) + 2f(3) + f(4)]\\\\= (1/2) * [5(0)(0^2) + 2(5)(1)(1^2) + 2(5)(2)(2^2) + 2(5)(3)(3^2) + 5(4)(4^2)]\\\\= (1/2) * [0 + 10 + 80 + 270 + 320]\\\\= (1/2) * 680\\\\= 340\)
Simpson's Rule:
Using n = 4, we divide the interval [0, 4] into four subintervals of equal width: h = (4 - 0) / 4 = 1.
The approximated value using Simpson's Rule is given by:
\(S_4 = (h/3) * [f(x_0) + 4f(x_1) + 2f(x_2) + 4f(x_3) + f(x_4)]\)
Plugging in the values:
\(S_4 = (1/3) * [f(0) + 4f(1) + 2f(2) + 4f(3) + f(4)]\\\\= (1/3) * [5(0)(0^2) + 4(5)(1)(1^2) + 2(5)(2)(2^2) + 4(5)(3)(3^2) + 5(4)(4^2)]\\\\= (1/3) * [0 + 20 + 40 + 360 + 320]\\\\= (1/3) * 740\\\\= 246.6667\)
Exact value of the definite integral:
∫[0, 4] 5x * \(x^2\) dx = [(5/4) * \(x^4\)] evaluated from 0 to 4
\(= (5/4) * 4^4 - (5/4) * 0^4\\\\= (5/4) * 256 - (5/4) * 0\\\\= 320 - 0\\\\= 320\)
Comparing the results:
Exact value of the definite integral = 320
Trapezoidal Rule approximation (n = 4) = 340
Simpson's Rule approximation (n = 4) ≈ 246.6667
As we can see, the Trapezoidal Rule approximation is slightly greater than the exact value, while Simpson's Rule approximation is less than the exact value.
To learn more about trapezoid visit:
https://brainly.com/question/1410008
#SPJ4
Which of the following statements is not true concerning the comparison of the bag weights for the two brands?
Almost 25% of the weights for brand B are less than the lowest weight for brand A.
About 50% of the weights for brand A are within the top 25% of the weights for brand B.
More than 75% of the weights for brand A are within the top 50% of the weights for brand B.
More than 75% of the weights for brand A are higher than the top 25% of the weights for brand B.
Answers
The statement "Almost 25% of the weights for brand B are less than the lowest weight for brand A" is not true concerning the comparison of the bag weights for the two brands, 1st option.
How does inequality work?Inequalities are mathematical expressions in which neither side is equal. Unlike equations, we compare two values in inequality. In between, the equal sign is replaced by a less than (or less than or equal to), greater than (or greater than or equal to), or not equal to sign.
In comparison to Brand B's box plot display, Brand A's rectangular box, as well as the length of the whiskers, are shorter. As a result, Brand A's bag weights are less variable than Brand B's bag weights.
Find out more on inequalities here: https://brainly.com/question/24372553
#SPJ1
The full question is:
Which of the following statements is not true concerning the comparison of the bag weights for the two brands?
Almost 25% of the weights for brand B are less than the lowest weight for brand A.
About 50% of the weights for brand A are within the top 25% of the weights for brand B.
More than 75% of the weights for brand A are within the top 50% of the weights for brand B.
More than 75% of the weights for brand A are higher than the top 25% of the weights for brand B.

PLEASEE HELPP !
Over which interval is the graph of f(x) = { x2 + 5x +
10
6 increasing?
8
6 • (0,6)
4
(-6.5, 0)
0 (-5)
(0, -5)
0 ( 0, -6.5)
2
-10 48 -6 4
2
4
6
8
10
X
4.
(-5, -6.5)
16
-8
w 10

Answers
Answer:
Option B
Step-by-step explanation:
For increasing function in the interval (a, b),
"If we draw a tangent at any point on the graph in the given interval (a, b), slope of the tangent drawn will be positive"
Given function is,
\(f(x)=\frac{1}{2}x^2+5x+6\)
In the interval (-∞, -5),
Graph is moving downwards therefore, tangents drawn at any point will have a negative slope and the function will decrease in this interval.
In the interval (-5, ∞),
In the given interval any tangent drawn at any point will have a positive slope and the function will be increasing.
Therefore, interval in which the function is increasing → (-5, ∞)
Option B is the answer.
The interval in which the function decreases is (-∞, -5).
In which interval the function decreases?The function decreases when, reading from left to right, the graph of the function goes downwards.
By looking at the graph, we can see that the graph goes downwards on the interval negative infinity and -5
Then we conclude that the function decreases on the interval (-∞, -5).
If you want to learn more about functions:
https://brainly.com/question/4025726
#SPJ5
Jonah’ cell phone came with 64
GB of memory. He ha ued 15 GB. He then ue 5 GB of memory to record photo and video from a trip. Ue the addition expreion 64 (-15) (-5) to find how much memory i left on hi phone
Answers
The memory that is left on his phone is 44gb.
Given that,
64 GB of capacity were included with Jonah's smartphone. He used 15GB total. He then recorded photos and videos from a vacation using 5 GB of memory.
Total Memory in his phone = 64gb
Jonah's used 15gb which means = 64 - 15 = 49gb
He then recorded photos and videos from a vacation using 5 GB of memory = 49 - 5 = 44Gb
The addition expression is 64-15-5 = 44gb.
Take -15 and -5 add them together get -20 then take 64 and subtract 20 leaving you with 44 GB left on his phone.
Therefore, the memory that is left on his phone is 44gb.
To learn more about expression click here:
brainly.com/question/14083225
#SPJ4
Given the following two side lengths of a triangle, what is the largest whole number length possiblefor the third side?6 and 12
Answers
Answer:
17
Step-by-step explanation:
\(6 + 12 > x\)
\(6 + x > 12 \)
From these, we have
\(6 < x < 18\)
Including a dependent variable that is NOT a scale variable _____ of the paired-samples t test, but does not preclude use of this test, because the paired-samples t test is a robust hypothesis test.
Answers
Including a dependent variable that is NOT a scale variable weakens the paired-samples t-test, but does not prevent its usage.
Although the paired-samples t-test is a robust hypothesis test, including a dependent variable that is not a scale variable may weaken it.
What is a paired-sample t-test?
The paired-samples t-test is a statistical procedure that compares two means using two sets of observations. It can be used to test whether the means of two paired groups are equivalent or different. Each pair of measurements is done on the same subject or entity, and the samples are correlated. In comparison to the unpaired t-test, the paired t-test increases the sensitivity of the analysis because it eliminates extraneous sources of variation between the two samples.
The t-statistic is a measure of the difference between two means relative to the variability within each group, and it is used to calculate the probability of obtaining such a large or larger difference by chance. Paired t-tests assume that the variables are scale variables. If any of the paired variables are not scale variables, the power of the test may be weakened, but the test may still be used.
The dependent variable should be a scale variable (continuous). A scale variable is one that has a range of values (e.g. weight, height, and age). The statistical technique works best with interval or ratio data. It can be used for data from a Likert scale, but only if the scale is treated as continuous and has at least five levels.
Learn more about dependent variable here:
https://brainly.com/question/17034410
#SPJ11
Can you help with my math problem

Answers
Answer:
Step-by-step explanation:
What you can do in this case is the following rule of three to find the result:
1 light year ---> 5.88 * 10 ^ 12 miles
3.2 * 10 ^ 2 light year ---> x
Clearing x we have:
x = ((3.2 * 10 ^ 2) / (1)) * (5.88 * 10 ^ 12)
x = 1.88 * 10 ^ 15 miles
answer:
In scientific notation, approximately it is 1.88 * 10 ^ 15 miles
Write the equation of the line that passes through the points
(0,8) and
(−1,−4). Put your answer in fully reduced point-slope form, unless it is a vertical or horizontal line.
Answers
Answer:
y + 4 = 12 ( x - 1 )
Step-by-step explanation:
→ Work out the gradient
\(\frac{-4-8}{-1-0} =12\)
→ Substitute the numbers into the y - y₁ = m ( x - x₁ )
y + 4 = 12 ( x - 1 )
–81, 108, –144, 192,. Which formula can be used to describe the sequence?.
Answers
The formula that can be used to describe the sequence is:\(a(n) = (-1)^(n+1) * 3^(n) * 4.\)
The given sequence is -81, 108, -144, 192.
The formula that can be used to describe the sequence is: \(a(n) = (-1)^(n+1) * 3^(n) * 4\), where n is the nth term in the sequence.
This formula is a geometric sequence formula that can be used to describe the given sequence.
The formula represents the nth term of the sequence as a function of the position of the term in the sequence.
Here, n represents the position of the term in the sequence
.For the given sequence, the first term is -81, which corresponds to the first position in the sequence (n = 1).
The second term is 108, which corresponds to the second position in the sequence (n = 2).
The third term is -144, which corresponds to the third position in the sequence (n = 3).
The fourth term is 192, which corresponds to the fourth position in the sequence (n = 4).
Therefore, the formula that can be used to describe the sequence is: \(a(n) = (-1)^(n+1) * 3^(n) * 4.\)
Know more about sequence here:
https://brainly.com/question/7882626
#SPJ11
Can someone please help me with this asap? I don’t understand it

Answers
Answer: C A B
Step-by-step explanation:
hope this helps
I need help with this question
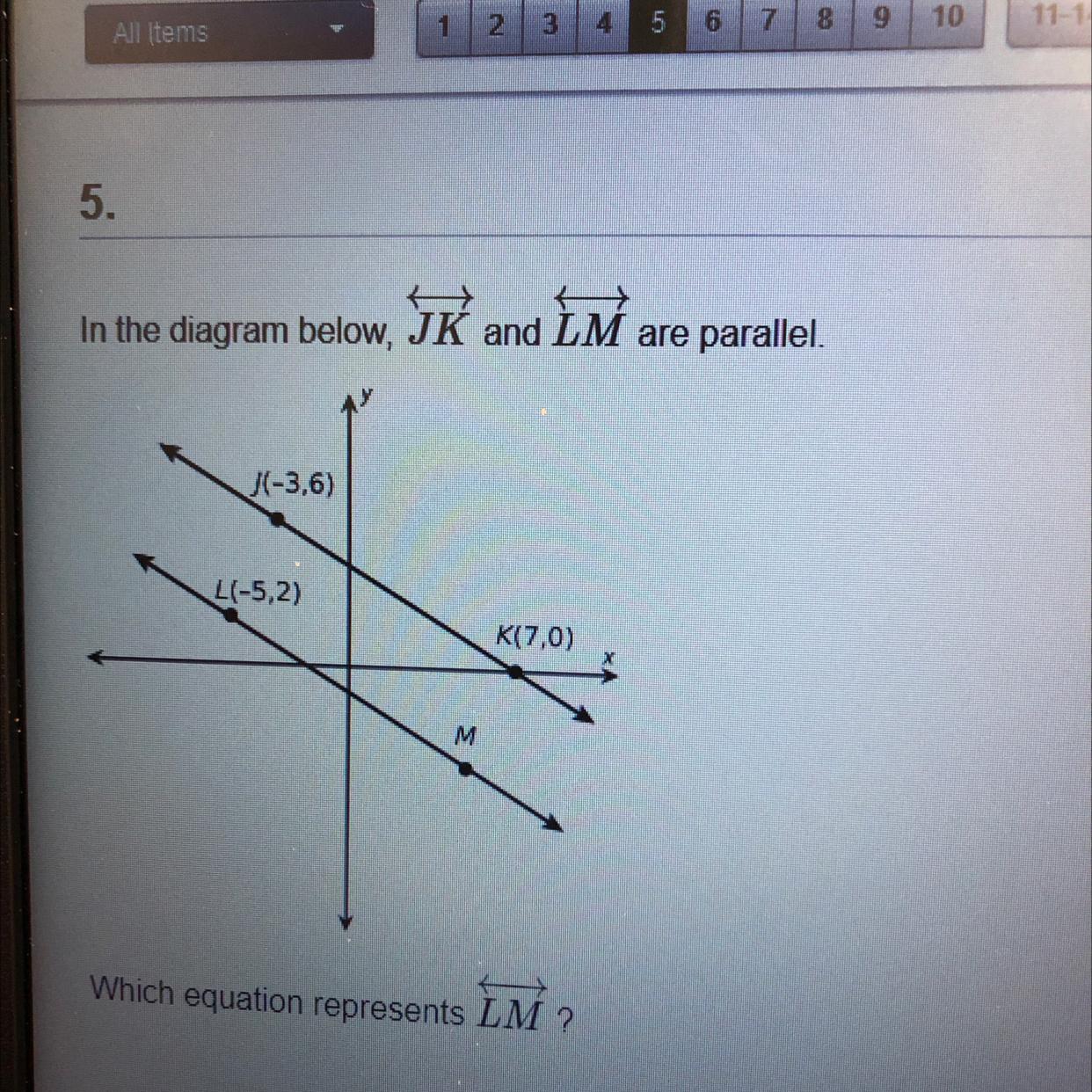
Answers
Answer:
-5,2
Step-by-step explanation:
it literally represents LM and Shows it on the graph
2(X+3)=x-4 and 4(5x-2)=2(9x+3)
Answers
Answer:
2x+10=x and 2x=14 this is what I got
Step-by-step explanation:
+
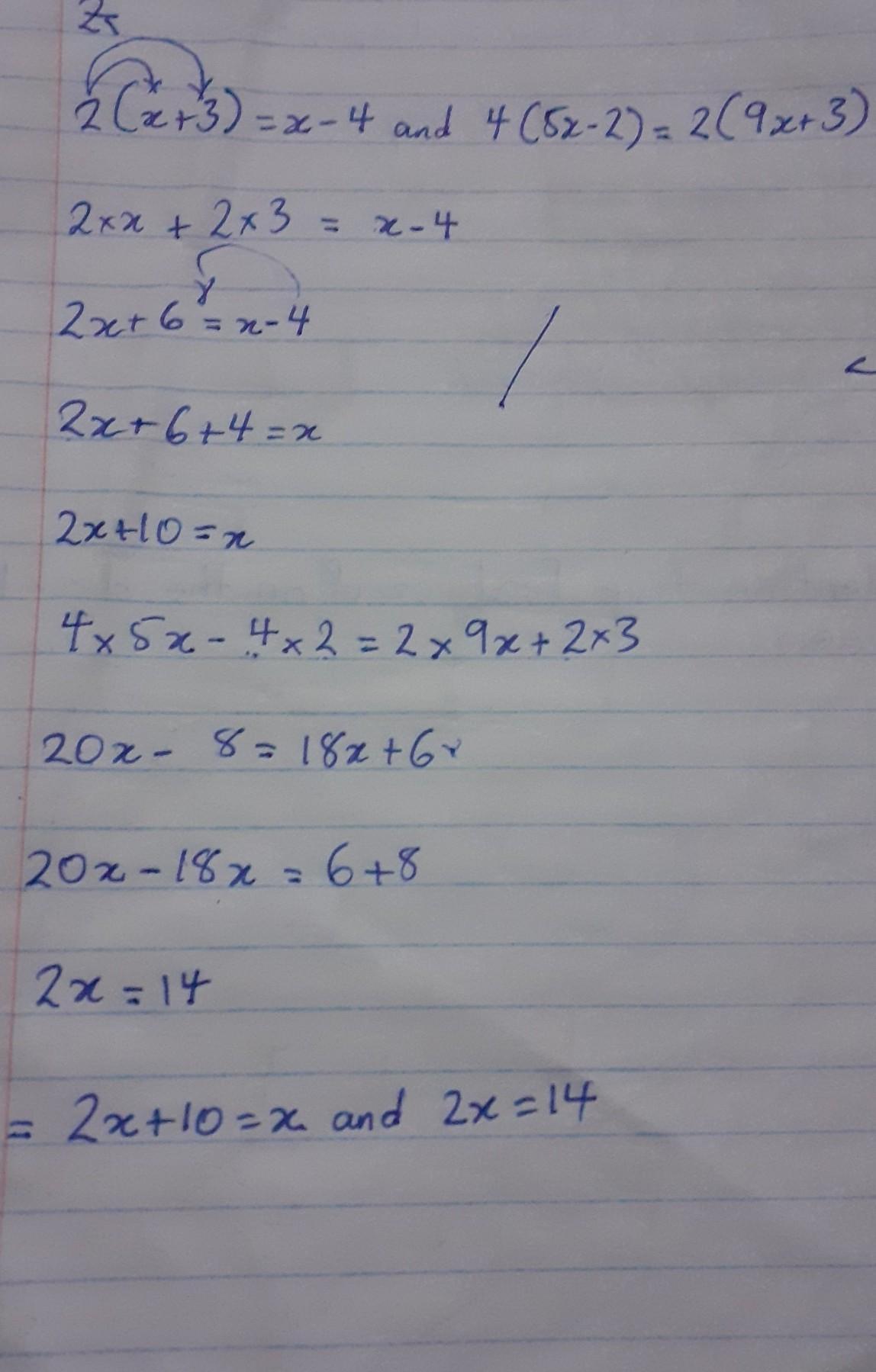
A soft drink vendor at a popular beach analyzes his sales records and finds that if he sells xcans of soda pop in one day, his profit (in dollars) is given by P(x) 0.001x2 3x 1800 What is his maximum profit per day, and how many cans must he sell to reach the maximum profit?
Answers
The soft drink vendor's maximum profit per day is $5250, and he must sell 1500 cans of soda pop to reach the maximum profit.
To find the maximum profit per day for the soft drink vendor, we need to use the formula P(x) = 0.001x^2 + 3x + 1800, where x is the number of cans of soda pop sold in one day.
To find the maximum profit, we need to find the vertex of the parabola represented by the profit function. The x-coordinate of the vertex is given by -b/2a, where a = 0.001 and b = 3. Plugging in these values, we get x = -3/(2*0.001) = -1500.
Since the soft drink vendor cannot sell a negative number of cans, we know that the maximum profit occurs at the closest whole number to x = -1500, which is x = 1500.
To find the maximum profit per day, we can plug in x = 1500 into the profit function:
P(1500) = 0.001(1500)^2 + 3(1500) + 1800 = $5250
Therefore, the soft drink vendor's maximum profit per day is $5250, and he must sell 1500 cans of soda pop to reach the maximum profit.
To find the maximum profit per day and the number of cans needed to reach that profit, we'll first need to find the critical point of the given quadratic profit function, P(x) = -0.001x^2 + 3x - 1800.
Step 1: Find the derivative of P(x) with respect to x. This will give us the rate of change of profit as the number of cans sold changes.
P'(x) = -0.002x + 3
Step 2: Set the derivative equal to zero and solve for x. This will give us the critical point where the maximum profit occurs.
-0.002x + 3 = 0
x = 1500 cans
Step 3: Substitute the critical point (x = 1500) back into the profit function P(x) to find the maximum profit.
P(1500) = -0.001(1500)^2 + 3(1500) - 1800
P(1500) = $600
So, the maximum profit per day is $600, and the soft drink vendor must sell 1500 cans to reach the maximum profit.
Learn more about profit at: brainly.com/question/15699405
#SPJ11
The maximum profit per day is $4800, and the vendor must sell 1500 cans of soda pop to reach this maximum profit.
The profit function for the soft drink vendor is given by:
P(x) = \(0.001x^2 + 3x + 1800\)
To find the maximum profit, we need to find the vertex of the parabola represented by this function. The x-coordinate of the vertex can be found using the formula:
x = -b / (2a)
where a = 0.001 and b = 3. Substituting these values, we get:
x = -3 / (2 * 0.001) = -1500
Since the value of x cannot be negative in this context, we know that the maximum profit occurs at x = 1500. To find the maximum profit, we substitute this value of x into the profit function:
P(1500) =\(0.001(1500)^2 + 3(1500) + 1800 = $4800\)
Therefore, the maximum profit per day is $4800, and the vendor must sell 1500 cans of soda pop to reach this maximum profit.
Learn more about maximum profit
https://brainly.com/question/29248429
#SPJ4
a student records the repair cost for 1717 randomly selected washers. a sample mean of $82.95$82.95 and standard deviation of $14.89$14.89 are subsequently computed. determine the 80�% confidence interval for the mean repair cost for the washers. assume the population is approximately normal. step 1 of 2 : find the critical value that should be used in constructing the confidence interval. round your answer to three decimal places.
Answers
The mean repair cost for the stereos is (63.04, 102.86) with an 80% confidence interval.
What is the critical factor?The critical factor for a 90% confidence interval for the true mean repair cost for stereos is given by;
Critical factor = (x-μ)/(s/√n)
where, x = sample mean repair cost
s = standard deviation of a sample
n = sample of stereos
μ = critical value
We have been given that a student records the repair cost for 17 randomly selected washers. a sample mean of $82.95 and a standard deviation of $14.89 are subsequently computed.
Since we don't know the population standard deviation, we used t statistics to create the 80% confidence interval in this case.
So, the 80% confidence interval for the true mean repair cost, μ is ;
⇒ P(-1.337< t₅ < 1.337) = 0.80
{As the critical value of t at 5 degrees of freedom are -1.337& 1.337 with P = 5%}
⇒ P(-1.337< (x-μ)/(s/√n) < 1.337) = 0.80
⇒ P(-1.337×(s/√n) < (x-μ) < 1.337×(s/√n)) = 0.80
⇒ P(x - 1.337×(s/√n) < μ < x + 1.337×(s/√n)) = 0.80
80% confidence interval for
⇒ μ = (x - 1.337×(s/√n) , x + 1.337×(s/√n))
Here, x = $82.95 , s = $14.89 , and n = 17
⇒ μ = (82.95 - 1.337×(14.89 /√17) , 82.95 + 1.337×(14.89 /√17))
⇒ μ = (63.04, 102.86)
Hence, the mean repair cost for the stereos is (63.04, 102.86) with a 80% confidence interval.
Learn more about the critical value here:
https://brainly.com/question/15417413
#SPJ4
I need some help with this.

Answers
Answer: 23
Step-by-step explanation:
The range of the data set is the same thing as subtracting the smallest value from the largest value.
Here, our smallest value is 8 and our largest value is 31.
31 - 8 = 23
This data set has a range of 23.
A flower shop charged $124.44 for 3 bouquets of flowers. This price included a $7.50 service and delivery fee.
What was the cost of one bouquet?
Answers
Planes the fly at high speeds and low elevations have radar systems that can determine the range of an obstacle and the angle of elevation to the top of the obstacle. The radar of a plane flying at an altitude of 20,000 feet detects a tower that is 25,000 feet away, with an angle of elevation of 1 $\degree$ . A picture shows a tower on a hill and a plane flying towards the tower, and a right angle is marked between plane and tower. Distance between plane and top of tower is 25 thousand feet and is the hypotenuse of the triangle, angle of elevation from plane to top of tower is labeled 1 degrees, and perpendicular height of the triangle from a point on the tower to top of the tower is h feet.
How many feet must the plane rise to pass over the tower?
Answers
Let AB be the tower with C at the top. Let P be the position of the plane such that the angle of elevation is 1°. Let the distance PC be h ft. The distance from the plane to the foot of the tower is 25,000 ft - the height of the plane above the ground (20,000 ft), which is 5,000 ft.
The distance PC is the same as the perpendicular height of the triangle. Therefore, `tan 1° = h / 25,000`. We can solve this equation for \(h: `h = 25,000 tan 1° ≈ 436.24 ft`.\) To find how many feet the plane must rise to pass over the tower, we need to find the length of the line segment CD,
which is the height the plane must rise to clear the tower. We can use trigonometry again: `tan 89° = CD / h`. Since `tan 89°` is very large, we can approximate `CD ≈ h / tan 89°`.Therefore, `\(CD ≈ 436.24 / 0.99985 ≈ 436.29 ft`\).Thus, the plane must rise approximately 436.29 feet to pass over the tower.
To know more about position visit:
https://brainly.com/question/12650352
#SPJ11