Which is the slope of the line that passes through the points (4, 2) and (6, 7)?
Answers
Answer:
\(\displaystyle m = 5\)
General Formulas and Concepts:
Pre-Algebra
Evaluations
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightAlgebra I
Coordinate Planes
Coordinate (x, y)Slope Formula: \(\displaystyle m = \frac{y_2 - y_1}{x_2 - x_1}\)
Step-by-step explanation:
Step 1: Define
Identify variables.
Point (4, 2)
Point (6, 7)
Step 2: Find slope m
Simply plug in the 2 coordinates into the slope formula to find slope m.
Substitute in points [Slope Formula]: \(\displaystyle m = \frac{7 - 2}{6 - 4}\)[Evaluations] Simplify: \(\displaystyle m = \frac{5}{1}\)[Evaluations] Simplify: \(\displaystyle m = 5\)Answer:
m = 5
Step-by-step explanation:
Step 1: DefineIdentify variables.
Point (4, 2)
Point (6, 7)
Step 2: Find slope mSimply plug in the 2 coordinates into the slope formula to find slope m.
Substitute in points [Slope Formula]:\(\displaystyle m = \frac{7 - 2}{6 - 4}m=6−47−2\)
[Evaluations] Simplify:\(\displaystyle m = \frac{5}{1}m=15\)
[Evaluations] Simplify:\(\displaystyle m = 5m=5\)
Related Questions
Rachel finished
3
_
4
of the race in 6 hours. How long was the entire race?
Answers
Answer:
8 hours
Step-by-step explanation:
Answer:
bjhmiukjgjhkuijkl
Step-by-step explanation:
Determine the level of measurement of the variable.Livability rankings for cities Choose the correct level of measurement.A. Ratio.B. Ordinal.C. Nominal.D. Interval.
Answers
Answer:
B. Ordinal
Step-by-step explanation:
The level of measurement used for a variable in statistical analysis determines what summary statistics and analysis are possible. In statistical analysis, we have three types of level of measurement.
Nominal , Ordinal , Interval/ Ratio
The nominal is the most basic level of measurement. It is the qualitative level of measurement such as color or number. Data in Nominal scale of measurement are stored as a word or as numerical code.
Ordinal level of measurement are variables based on ranks or hierarchy. Ordinal level of measurement posses a sequential step-wise order but the intervals between the variables are not equal. They are usually expressed in frequencies.
Therefore, the level of measurement of variable that determines the livability rankings for cities based on their ranks or hierarchy is Ordinal.
The interval/ratio level of measurement is the highest level of measurement where data are being measured and ordered in a sequential process.
Solve for h -110=13+3(4h-6)
Answers
Answer:
H= -35/4
Decimal form: -8.75
Explanation:
Subtract 13 from both sides. { -110 - 13 =3(4h - 6) }Simplify -110 -13 to -123 { -123 = 3 (4h - 6) }Divide both sides by 3 { -123/3 = 4h - 6 }simplify 123/3 to 41 { -41 = 4h - 6 }add 6 to both sides { -41 +6 = 4h }simplify -41 + 6 to -35 { -35 = 4h }divide both sides by 4 { - 35/4 = h }switch sides { h= - 35/4 }Bridgette’s market sold 36 avocados one morning. That afternoon 2/7 of the remaining avocados were sold. The number of avocados left was now 1/2 of the number the market had at the beginning of the day. How many avocados were ther at the beginning of the day?
Answers
Answer:
120
Step-by-step explanation:
Sold = 36
remaining = x - 36
Evening = 2/7 × (x - 36)
(2x - 72)/7
36 + (2x - 72)/7 = x/2
2x + 180)/7 = x/2
4x + 360 = 7x
4x - 7x = -360
x = 120
I need help please with number 5 and 6

Answers
Answer: #5 = -3 #6 = 0, there is no x
Step-by-step explanation: #5 - first you have to turn it into slope-intercept form. So, 3y+12=-9x will become y= -3x -4 because you divide all sides by 3 and you transpose 12 so it becomes negative... then you will pick out you slope which is the number in front of x so slope = -3
#6 - the slope is zero because there is no x in that equation.
6. I got Y=-4
Select the values that make the inequality -q> -7 true. Then write an equivalent inequality, in terms of q. (Numbers written in order from least to greatest going across.)

Answers
The inequality relation -q > -7 can be represented in the form of q as q < 7
The numbers in set A = { -8 , -7.1 , -7 , -6.9 , -6 , -2 , 0 , 2 , 6 , 6.9 }
What is an Inequality Equation?
Inequalities are the mathematical expressions in which both sides are not equal. In inequality, unlike in equations, we compare two values. The equal sign in between is replaced by less than (or less than or equal to), greater than (or greater than or equal to), or not equal to sign.
In an inequality, the two expressions are not necessarily equal which is indicated by the symbols: >, <, ≤ or ≥.
Given data ,
Let the inequality equation be A
The value of A is - q > - 7
Now , multiplying by (-1) on both sides of the equation , we get
( -1 ) ( -q ) > ( -1 ) ( - 7 )
The inequality relation will change the sign from > to < and ,
q < 7
So , the value of the inequality relation A is q < 7
Now , all the values in the number line which satisfy the inequality equation q < 7 are given in set A
The numbers in set A = { -8 , -7.1 , -7 , -6.9 , -6 , -2 , 0 , 2 , 6 , 6.9 }
Hence , The inequality relation -q > -7 can be represented in the form of q as q < 7 and numbers in set A = { -8 , -7.1 , -7 , -6.9 , -6 , -2 , 0 , 2 , 6 , 6.9 }
To learn more about inequality equations click :
https://brainly.com/question/11897796
#SPJ1
This table shows values represented by an exponential function.
x | y
0 | 3
2 | 9
3 | 27
4 | 64
5 | 125
6 | 216
What is the average rate of change for this function for the interval from x=2 to x=4?
A. 18
B. 27.5
C. 55
D. 36.5
Answers
The average rate of change for this function for the interval from x=2 to x=4 is B. 27.5.
What is the average rate?The average rate at which one quantity changes in relation to another's change is referred to as the average rate of change function.
A method that determines the amount of change in one item divided by the corresponding amount of change in another is known as an average rate of change function.
For this special case from the info in the table, we have:
a = 2, f(2) = 9
b = 4, f(4) = 64
And replacing the data into the average rate formula we got:
m = 64-9/4-2 = 27.5
Thus, the correct option is B. 27.5.
Learn more about the average rate, here:
https://brainly.com/question/28026065
#SPJ1
Find two numbers whose sum is 8 and whose product is 17
Answers
Answer:
Step-by-step explanation:
x+y = 8
y = 8-x
xy = 17
x(8-x) = 17
8x - x² = 17
x² - 8x + 17 = 0
Quadratic formula
x = [8 ± √(8² – 4·1·17)] / [2·1]
= [8 ± √(-4)] / 2
= [8 ± 2i] /2
= 4±i
x = 4+i
y = 4-i
A quadratic equation is written in the form of ax²+bx+c. The two numbers whose sum is 8 and whose product is 17 are (4+i) and (4-i).
What is a quadratic equation?A quadratic equation is an equation whose leading coefficient is of second degree also the equation has only one unknown while it has 3 unknown numbers. It is written in the form of ax²+bx+c.
Let the first number be 'a' and the second number be 'b'. Therefore, the sum of the two numbers is,
a+b=8
The product of the two numbers is,
ab=17
b=17/a
now, the equation can be written as,
a+b=8
a+(17/a)=8
a² + 17 = 8a
a²-8a+17=0
a = 4±i
Hence, the two numbers whose sum is 8 and whose product is 17 are (4+i) and (4-i).
Learn more about Quadratic Equations:
https://brainly.com/question/2263981
#SPJ2
Which equation could generate the curve in the graph below?
On a coordinate plane, a parabola opens down. The parabola is in quadrants 2 and 3, and has its vertex in quadrant 2.
y = –2x2 + 3x – 5
y = –2x2 – 4x – 2
y = –2x2 – 16x– 28
y = –2x2 +16x –28
Answers
Answer:
Its C boys
Step-by-step explanation:
I graphed all of them and compared
The equation that could represent the graph of the parabola is (c) \(y = -2x^2 - 16x- 28\)
From the question, we have the following highlights
The parabola opens downThe vertex is in the second quadrantThe second highlight above means that:
The x coordinate (h) of the vertex is negative, while the y-coordinate (k) is positive.
For a parabola: \(y = ax^2 + bx + c\), the vertex is:
\((h,k) = (-\frac{b}{2a},f(h))\)
Next, we test the options
(a) y = –2x2 + 3x – 5
We have:
\(h = -\frac{3}{-2 \times 2}\)
\(h = 0.75\)
The value of h is positive.
So, this cannot represent the parabola
(b) y = –2x2 – 4x – 2
We have:
\(h = -\frac{-4}{-2\times 2}\)
\(h = -1\)
Substitute -1 for x in the function
\(k = -2x^2 - 4x - 2\)
\(k = -2(-1)^2 - 4(-1) - 2\)
\(k = 0\)
The value of k cannot be 0
So, this cannot represent the parabola
(c) y = –2x2 – 16x– 28
We have:
\(h = -\frac{-16}{-2\times 2}\)
\(h = -4\)
Substitute -4 for x in the function
\(k = -2x^2 - 16x- 28\)
\(k = -2(-4)^2 - 16(-4)- 28\)
\(k=4\)
The x coordinate (h) of the vertex is negative, while the y-coordinate (k) is positive.
Hence, \(y = -2x^2 - 16x- 28\) could represent the parabola
Read more about parabola at:
https://brainly.com/question/17987697
f(x)= a(x+p)² +q and g(x)= 0 3 3.1 x + p 1. The turning point of f is (1;4) and the asymptotes of g intersect at the turning point of f. Both graphs cut the y-axic at 3. 3.2 3.3 3.4 a 10 g +94 (1:4) Determine the equation of f Determine the equation of g Determine the coordinates of the x-intercept of g For which values of x will f(x) ≥ g(x)? [9]
Answers
Step-by-step explanation:
Let's solve the given questions step by step:
1. Determine the equation of f:
From the given information, we know that the turning point of f is (1, 4). The general form of a quadratic function is f(x) = ax^2 + bx + c. We are given that f(x) = a(x + p)^2 + q, so let's substitute the values:
f(x) = a(x + p)^2 + q
Since the turning point is (1, 4), we can substitute x = 1 and f(x) = 4 into the equation:
4 = a(1 + p)^2 + q
This gives us one equation involving a, p, and q.
2. Determine the equation of g:
The equation of g is given as g(x) = 0.3x + p1.
3. Determine the coordinates of the x-intercept of g:
The x-intercept is the point where the graph of g intersects the x-axis. At this point, the y-coordinate is 0.
Setting g(x) = 0, we can solve for x:
0 = 0.3x + p1
-0.3x = p1
x = -p1/0.3
Therefore, the x-intercept of g is (-p1/0.3, 0).
4. For which values of x will f(x) ≥ g(x)?
To determine the values of x where f(x) is greater than or equal to g(x), we need to compare their expressions.
f(x) = a(x + p)^2 + q
g(x) = 0.3x + p1
We need to find the values of x for which f(x) ≥ g(x):
a(x + p)^2 + q ≥ 0.3x + p1
Simplifying the equation will involve expanding the square and rearranging terms, but since the equation involves variables a, p, and q, we cannot determine the exact values without further information or constraints.
To summarize:
We have determined the equation of f in terms of a, p, and q, and the equation of g in terms of p1. We have also found the coordinates of the x-intercept of g. However, without additional information or constraints, we cannot determine the exact values of a, p, q, or p1, or the values of x for which f(x) ≥ g(x).
An airplane on autopilot took 5 hours to travel 3,640 kilometers. What is the unit rate for kilometers per hour?
The unit rate is
kilometer(s) per hour.
Answers
3640 divided by 5 to find the unit rate for kilometers per hour
Solve: 7|x| = 42
36
–6 or 6
no solution
6
Answers
Answer:
6
Step-by-step explanation:
7×6=42 so 6 is x so this is your answer
Answer:
-6 or 6
Step-by-step explanation:
7x|x|=42 (divide both sides)
|x|=6 (separate into possible cases)
x=6
x=-6 (the equation has two solutions)
hope this helps!
Solve 2(2x-5)=3x+x-2x
Answers
Answer:
5=x
Step-by-step explanation:
Q=2(2x-5)=3x+x-2x
SOLUTION:
4x-10=4x-2x
-10=2x-4x
-10= -2x
(-+-=+ so 10 and 2 are positive now)
10/2=x
5=x
Triangle A B C is reflected across the line of reflection m to form triangle A prime B prime C prime. Triangle A prime B prime C prime is rotated about point B prime 270 degrees to form triangle A double-prime B double-prime C double-prime.
Which rule describes the composition of transformations that maps ΔABC to ΔA"B'C"?
Answers
Answer:
it is D trust me
Step-by-step explanation:
Answer:
the answer is d
Step-by-step explanation:
the way you can figure this out is by looking at the figures and finding what transformation came first because of the number of prime notations on a letter in a figure. in this case is was ABC first then A'B'C' then A''B''C''
using that we can now determine the order of how the composition will be written. the first step of the composition is the left most part and the last part of the composition is the right most part. basicly the order is left to right.
we see that figure ABC is reflected across the line m to create the figure A'B'C' relections are written like r for the relection and the sub letter is the line the figure is reflected across to in this case it would be written as r sub m meaning that r sub m is the 2nd part of the composition.
the 2nd step in the composition is when figure A'B'C' turns into figure A''B''C'' the way we find out its transformation is determine whether it was slid or if it was rotated aroound a point of rotation. here we have a rotation. now we got to determine what the center of roation is. in this case its B'. looking at the options there is no negative -90 degrees which means that the rotation happened counter clockwise because all valuse are positive. counter clockwise is to the left. now simple math figure A'B'C 180 degrees would make it need 90 more degrees so 180+90=270 thats the degree of the roation around point B'
rotations are written as R sub point of rotation, __ degrees. in our case it is r sub B', 270 degrees. this is the second step so it will be on the right of the equation. the full equation turns out to be R sub B', 270 degrees composition of transformations r sub m.
it must be that way because if you rotated the figure first then reflected it it would look like an entirely different image.
pls give brainliest
CAN U HELP I WILL GIVE 20 POINTS

Answers
Answer:
Your pay rate would be $7 per hour
Your friend's rate is $9 per hour
Step-by-step explanation:
To get the answer for your pay rate you'll have to divide 56/8 and then you'd get your number 7, so you get $7 dollars per hour.
To get the number for your friends pay rate you'd also do the same thing, divide. 36/4 gives you the number 9, so your friend gets $9 dollars per hour.
~PLZ give brainliest only if this is correct, thx!~
A factory that produces toy wheels finds that they must discard 3 out of 100 wheels because they are defective. How many wheels would they expect to discard everyday if the factory produces 1200 wheels per hour in each 8 hr day.
Answers
they expect to discard everyday 288.
What is multiplication?In mathematics, multiplication is a method of finding the product of two or more numbers. It is one of the basic arithmetic operations, that we use in everyday life.
here, given that,
they must discard 3 out of 100 wheels because they are defective.
the factory produces 1200 wheels per hour in each 8 hr day.
total per day = 9600
so, they expect to discard everyday =9600 * 3%
=288
hence, they expect to discard everyday 288.
To learn more on multiplication click:
brainly.com/question/5992872
#SPJ1
if it is given that "x" is 23.5 - proof that it is a point of intersection at y= 1/2(x) - 25 if y is equal to 11. been trying but not working out.
Answers
When substituting y = 11 into the equation y = 1/2(x) - 25, we find that x = 72, confirming that (23.5, 11) is a valid point of intersection.
Given that x is 23.5, it is required to prove that it is an intersection point for the equation y = 1/2(x) - 25 when y is equal to 11.
The equation is given as y = 1/2(x) - 25
When y = 11, we can substitute the value of y in the equation to obtain 11 = 1/2(x) - 25
This can be simplified as 11 + 25 = 1/2(x)36 = 1/2(x)
On solving, x = 72Thus, when y is equal to 11 and x is equal to 72, the given point of intersection is valid.
Therefore, it can be concluded that x = 23.5 is a point of intersection for the equation y = 1/2(x) - 25 when y is equal to 11.
In summary, when given an equation with two variables, we can find the point of intersection by setting one of the variables to a given value and solving for the other variable. In this case, when y is equal to 11, we can solve for x and obtain the point of intersection as (72,11).
For more questions on intersection
https://brainly.com/question/30429663
#SPJ8
HELP IF U GET IT RIGHT ILL GIVE U BRAINLY PLEASE ONLY DO IF YOU KNOW HOW TO DO IT !!!!

Answers
Answer:
-8 ≤ y ≤ 7
Step-by-step explanation:
Which expression is equivalent to (2x – 5)(x + 9)?
Answers
Answer:
\(2x^{2} +13x-45\)
Step-by-step explanation:
By using FOIL method.
Evaluate 51x3 - 21 + 7 when x = -2.
DONE
Answers
Answer:
-320 i guess
Step-by-step explanation:
51*-2*3-21+7=-320
Please help me!!
A. Identify the quadrant point C is in. B. Identify the point that is on an axis. Which axis is it?

Answers
Answer:
Quadrant 2, x-axis
Step-by-step explanation:
Point C is on top left side of the x-y graph, which is quadrant 2.
An axis refers to line, so the x axis the is horizonal line, as it says on the right end of it. The y axis is the vertical line, noted at the top of the line.
The only line that's on a line is point D and it's on the x-axis.

Please help I’m struggling

Answers
The parametric equations are therefore: x is t, y is 1/3 * t, and z is t.
What is parametric equations?Response: x = t; y = 1/3; t; z = t
Given
At t = 0, r(t) equals f(t) * I + g(t) * j + h(t) * k.
(F (t0), G (t0), and H (t0))
r(t) = ln (t - 1) + (t + 2) * j + t * ln(tk) t * t * 0 = 1 Required Information is Missing
Calculate the parametric equations.
j + t * ln + (t - 1)/(t + 2) * ln + r(t) = ln(ti) (tk)
With regard to t, differentiate (t) = 1/t * I + 3/((t + 2) 2) * j + (ln(t) + 1) Let t=1 (i.e., e * t * t * 0 = 1)
r = 1/1 for prime (1). * I + 3/((1 + 2) ^ 2) * j + (ln(1) + 1) I + 3/(3 2) * k r prime (1) * j + (0 + 1) Prime (1) = I + 3/9 * K R * j + (1) (1) Prime (1) = I + 1/3 * j + * k r (1) I + 1/3 * j + k = * k r prime (1)
To find x, y, and z.
We utilise the following methods to find x, y, and z: r(t) = f(t) (t) * j + h (t) * k + I + g (t)
This suggests that:
prime r (1) * T = xi, yj, and zk
We therefore have:
I + 1/3 * j + k) = xi + yj + zk * t
it + 1/3 * jt + kt = xi + yj + zk.
In contrast:
xi = it
Divide by I x, y, and j to get 1/3 * jt.
Divide by j y = 3/9 * t zk = kt
Divided by k, z equals t.
The parametric equations are therefore: x = t, y = 1/3 * t, and z = t.
To learn more about parametric equations refer to:
https://brainly.com/question/51019
#SPJ1
10. Prime numbers from 1 to 100 are running a restaurant - PRIME SPOT, near a tourist point. On a winter holiday, 1 and the composite numbers up to 100 enter the restaurant for dinner after their picnic at the same point. The dining hall has tables with seating capacity 15 for each. If they occupy tables without leaving any chair free, how many tables are required? If each prime number attender has to serve equal number of customers, how many customers should each one get to serve?
Answers
6 tables are required. Each prime number attender should serve 3 customers each.
The prime numbers between 1 and 100 are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
All the numbers other than prime numbers are composite numbers.
The composite numbers from 1 to 100 are: 1, 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100.
Now, as there are 25 primes and 75 composites in the group that visited the restaurant, we can calculate the number of tables required by dividing the number of people by the seating capacity of each table.
Each table has a seating capacity of 15, so the number of tables required will be: Number of tables = (Number of customers)/(Seating capacity of each table)Number of customers = 25 (the number of primes) + 75 (the number of composites) = 100Number of tables = 100/15 = 6 tables
Therefore, 6 tables are required.
Now, as each prime number attender has to serve an equal number of customers, we need to calculate how many customers each one should serve.
Each prime attender has to serve 75/25 = 3 customers each, as there are 75 composites and 25 primes.
Thus, each prime number attender should serve 3 customers each.
For more questions on prime number
https://brainly.com/question/145452
#SPJ8
Help me answer this please

Answers
The area of the sector in terms of π is 35.6π inches squared.
The area of the sector is approximately 111.6 inches square
How to find the area of a sector?The area of sector of a circle is the amount of space enclosed within the boundary of the sector.
Therefore,
area of a sector = ∅ / 360 × πr²
where
r = radius∅ = central angleTherefore,
∅ = 200 degrees
r = 8 inches
area of the sector = 200 / 360 × 8²π
area of the sector = 200 / 360 × 64π
area of the sector =12800π/ 360
area of a sector = 35.6π inches squared
Let's find the area of the sector with π = 3.14
area of a sector = 35.6 × 3.14 = 111.6 inches square
learn more on sector here: https://brainly.com/question/22972014
#SPJ1
Find value of b and A
Answers
Answer:
Hi
Step-by-step explanation:
Please paste your question so I can solve it
Thanks
what is (1/2 + isqrt3/2)^5?
Answers
Answer:
\((\frac{1}{2}+\frac{\sqrt{3}}{2}i)^5=\frac{1}{2}-\frac{\sqrt{3}}{2}i\)
Step-by-step explanation:
Convert 1/2 + i√3/2 to rectangular form
\(\displaystyle z=a+bi=\frac{1}{2}+\frac{\sqrt{3}}{2}i\\\\r=\sqrt{a^2+b^2}=\sqrt{\biggr(\frac{1}{2}\biggr)^2+\biggr(\frac{\sqrt{3}}{2}\biggr)^2}=\sqrt{\frac{1}{4}+\frac{3}{4}}=\sqrt{1}=1\\\\\theta=\tan^{-1}\biggr(\frac{b}{a}\biggr)=\tan^{-1}\biggr(\frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}\biggr)=\tan^{-1}(\sqrt{3})=\frac{\pi}{3}\\\\z=\cos\frac{\pi}{3}+i\sin\frac{\pi}{3}\)
Use DeMoivre's Theorem
\(\displaystyle z^n=r^n(\cos(n\theta)+i\sin(n\theta))\\\\z^5=1^5\biggr(\cos\biggr(\frac{5\pi}{3}\biggr)+i\sin\biggr(\frac{5\pi}{3}\biggr)\biggr)\\\\z^5=\frac{1}{2}-\frac{\sqrt{3}}{2}i\)
The spring concert at a certain high school sold 155 tickets. Students were charged $4 each and adults $8 each. The income from the sale of tickets was $980. How many students and how many adults bought tickets? Use algebra to solve this problem.
Answers
Answer:
Step-by-step explanation: 85 students and 80 adults
Please answer this correctly
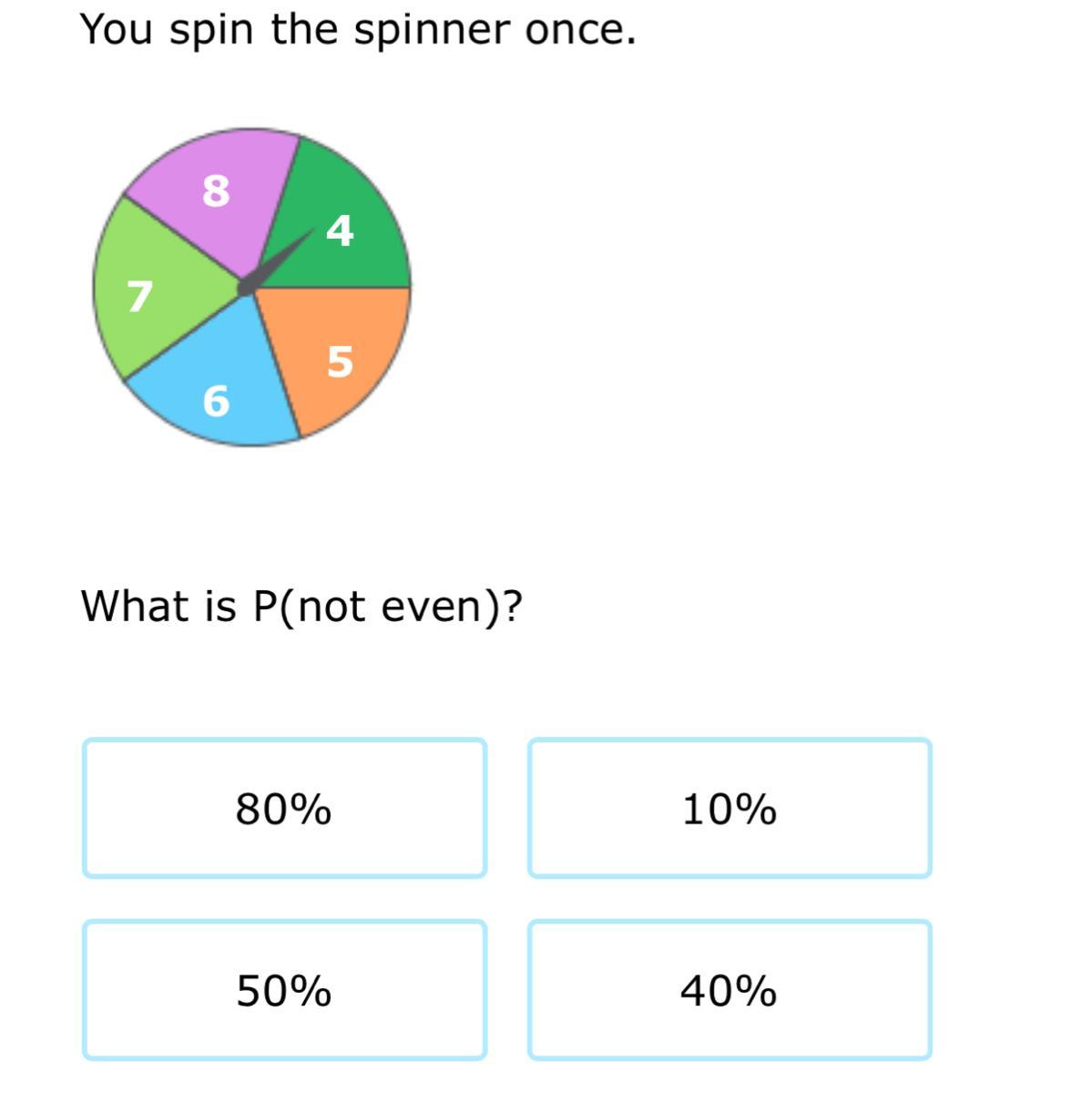
Answers
Answer:
40%
Step-by-step explanation:
The numbers that are not even are 5 and 7.
2 numbers out of 5.
2/5 = 0.4
P(not even) = 40%
Answer:
\(40\%\)
Step-by-step explanation:
5 and 7 are not the numbers
There are 5 numbers in the spinner
\(p = \frac{2}{5} \\ = \frac{2 \times 20}{5 \times 20} \\ = \frac{40}{100} \\ = 40\%\)
What is the volume of a sphere with radius 9? Round to the tenths.
Answers
Answer:
V=3053.6
Step-by-step explanation:
Ben is using a map. Let x represent a distance in centimeters on the map. To find an actual distance y in kilometers, Beth uses the equation y=8x
Answers
The table that can be constructed with the following equation has vales x: 0, 1, 2, 3 and y = 0, 8, 16, 24.
A linear equation is what?When the greatest power of the variable is consistently 1, an equation is considered to be linear. A one-degree equation is another name for it. The typical form of a linear equation with one variable is Ax + B = 0.
The slope of the linear relationship is eight. The solution is below, along with a picture of the line.
Substitute different values of x to obtain value of y:
The table is given below:-
x I y
-------
0 I 0
1 I 8
2 I 16
3 I 24
Learn more about graph here:
https://brainly.com/question/10712002
#SPJ1
The complete question is:
