Answers
Answer:
it might be c I'm not to sure tho
Related Questions
What is the side length of the smallest square plate on which a 38-cm chopstick can fit along a diagonal without any overhang?
Answers
The smallest square plate that can fit a 38 cm chopstick diagonally without overflow is about 26.84 cm.
What is a square and a formula?
A square is a special rectangle (equilateral) and a special parallelogram (equilateral and equiangular). A square has four axes of symmetry and its two terminal diagonals (as with any rectangle) are equal. The formula for the area of a square
The area of a square is equal to (side) × (side) square units. The area of a square, given the diagonal d, is d2÷2 square units. For example, the area of a square with 8 feet on each side is 8 × 8, or 64 square feet (ft2). Suppose the side length of a square plate is 'x' cm.
The length of the diagonal of a square plate is equal to the length of a chopstick, which is 38 cm.
So, according to the Pythagorean theorem, we can write:
x² + x² = 38²
Simplifying this equation, we get:
2x² = 1444
x² = 722
Taking the square root of both sides gives us:
x = 26.84 cm
Therefore, the side length of the smallest square plate on which a 38 cm chopstick can fit diagonally without crossing is about 26.84 cm.
Learn more about parallelogram here
https://brainly.com/question/29147156
#SPJ1
A floor has a shape of a trapezium Gary is going to paint the floor each 5 litre tin of paint cost 21.99 1 litre of paint covers an area of 2.5m

Answers
Answer:
Step-by-step explanation:
step 1 : finding the area of a floor using trapezius area formula
A= \(\frac{(10+14)*6}{2} = \frac{24*6}{2} =72 m^{2} \\\)
step 2 : the problem said 1 litre of paint convers an area of 2.5 m^2, so let's calculate how many liters of paint are needed to paint the floor
\(\frac{72 m^2}{2.5 m^2} = 28.8 litre\\\)
so we need 28.8 litre to paint the floor
step 3 : Each tin is 5 litre of paint so let's calculate how many tins do we need
n=\(\frac{28.8}{5} = 5.76 \\\)
we can't by 5.76 tins so it's 6 tins
step 4 : Each tin costs 21.99 and now we calculate how much 6 tins cost for us
cost = 6 × 21.99 = 131.94
step 5 : Gary has a budget of 150 and the total cost is 131.94. So, Gary has enough money to buy all the paint he needs.
which number best represents the slope of the graphed line?
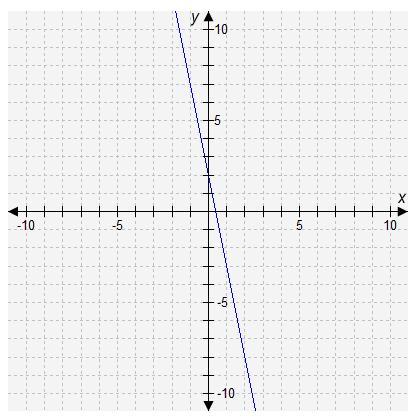
Answers
Answer:
If you have choices it is either -5 or 5.
Step-by-step explanation:
First, you find two points, which mine were (0,2) and (-1,7). The slope formula is y2 - y1 divided by x2 - x1. So, im going to subtract 7 - 2, which is your y2 - y1, to get 5. Then, i'm going to subtract -1 - 0, which is your x2 - x1, to get -1. Then, you divide 5 by -1 to get -5. I Hope This Helps :)
the gram-schmidt process produces from a linearly independent set {x1, x2, . . . , xp} an orthogonal set {v1, v2, . . . , vp} with the property that span{v1, . . . , vk}
Answers
The statement is true.
An orthogonal set with the same dimension as the initial collection of vectors is created by the Gram-Schmidt process.
Given that,
From a linearly independent collection of {x₁, x₂,..., xp}, the gram-Schmidt process creates an orthogonal set of {v₁, v₂,..., vp} with the feature that for each k, the vectors v₁...vk span the same subspace as that spanned by x₁...xk.
Whether the claim is true or false must be determined.
The statement is true.
An orthogonal set with the same dimension as the initial collection of vectors is created by the Gram-Schmidt process. An orthogonal set is further linearly independent. The orthogonal set produced by the Gram-Schmidt process and the original set will cover the same subspace if their dimensions are the same.
To learn more about orthogonal visit: https://brainly.com/question/2292926
#SPJ4
Plz help and ignore the equations below

Answers
Answer:
x = 8.5
Step-by-step explanation:
You have all three angles already, so it's easy: 90°, (4x - 8)°, (6x + 13)°
The sum of all angles is 180°
90 + (4x - 8) + (6x + 13) = 180
10x + 95 = 180
- 95 -95
10x = 85
x = 8.5
A piece of timber is
x
cm long.
How long would 3 pieces of timber be put together in a line?
Answers
Answer:
3x cm long.
Step-by-step explanation:
If one piece is x cm
and there are 3 together, presumeabley the same length
then you'd just need to multiply the length 3 times, therefore 3x respresents multiplying x 3 times.
Have a good day!
Answer:
3x cm long
Step-by-step explanation:
3 times x is 3x
Natasha was thinking of a number.
Natasha adds 11 to it, then doubles it
and gets an answer of 78.2. What was the number
Answers
Answer:
28.1
Step-by-step explanation:
You can answer questions like this by working backwards.
To do this we can divide 78.2 by 2 and that gets us 39.1
Now we have to subtract 11 from it and that gets us our final answer:
28.1
Answer:
She was thinking of the number 28.1
Step-by-step explanation:
Since we do not initially know what number Natasha was thinking of we have to start with 78.2. From here we have to do the reverse operations of what Natasha did.
So we would divide 78.2 by 2 which gives us 39.1
Then we minus 11 from that and we get 28.1
In the figure shown below, all the corners form right angles. What is the area of the figure?
15 ft
B.
44 ft²
17 ft
215 ft2
5 ft
7 ft
Answers
Based on the dimensions of the shape, the area of the figure can be found to be 215 ft².
How to find the area of the figure?To find the area of the figure, you can divide the shape into two different shapes and then find the area of those shapes, and then sum them up to find the area of the entire figure.
As shown in the attached photo, you can divide the figure into two rectangles with the dimensions:
15 ft and 12 ft (17 - 5)7 ft and 5 ftThe areas are:
= 15 x 12
= 180 ft²
Second rectangle:
= 7 x 5
= 35ft²
The area of the figure is:
= 35 + 180
= 215 ft²
Find out more on area at https://brainly.com/question/11423300
#SPJ1


Use the information to evaluate and compare Δy and dy. (Round your answers to four decimal places.)
y = x4 + 7 x = −2 Δx = dx = 0.01
Δy =?
dy =?
Answers
Δy=v-0.32 and dy = -0.32 .Δy and dy are both used to represent changes in the dependent variable y based on changes in the independent variable x.
Δy represents the change in y (the dependent variable) resulting from a specific change in x (the independent variable). In this case, y = x^4 + 7, x = -2, and Δx = dx = 0.01. Therefore, we need to calculate Δy and dy based on these values.
To calculate Δy, we substitute the given values into the derivative of the function and multiply it by Δx. The derivative of y = x^4 + 7 is dy/dx = 4x^3. Plugging in x = -2, we have dy/dx = 4(-2)^3 = -32. Now, we can calculate Δy by multiplying dy/dx with Δx: Δy = dy/dx * Δx = -32 * 0.01 = -0.32.
On the other hand, dy represents an infinitesimally small change in y due to an infinitesimally small change in x. It is calculated using the derivative of the function with respect to x. In this case, dy = dy/dx * dx = 4x^3 * dx = 4(-2)^3 * 0.01 = -0.32.
Therefore, both Δy and dy in this context have the same value of -0.32. They represent the change in y corresponding to the change in x, but Δy considers a specific change (Δx), while dy represents an infinitesimally small change (dx) based on the derivative of the function.
Learn more about derivative here:
https://brainly.com/question/32527348
#SPJ11
please help with math!!

Answers
Answer:
Trinomial
Step-by-step explanation:
If there is 1 term, monomial
2 term - binomial
3 term- trinomial
5 times the cube of x divided by 4 times x
Answers
Answer:
5x^2/4
Step-by-step explanation:
5 times the cube of x divided by 4 times x
(5x^3)/4x=5x^2/4
Answer:
I'm not sure what the question is... but I'm guessing you have to put this in number form? If so, the answer would be 5x^3/4x
Step-by-step explanation:
When having a number times x instead of writing the multiplication sign you just put them next to each other. (5x)
When something is cubed that means it is to the power of three (5x^3)
Divided by four times x would be 4x
Hopefully I did this right and helped you!
in a binomial experiment, the number of successes can never exceed the number of trials. (True or False)
Answers
Answer: True
Step-by-step explanation:
Which number line correctly shows 4.5 – 2.5?
a) A number line going from 0 to 4.5 in increments of 0.5. An arrow goes from 0 to 4.5 and then backwards from 4.5 to 2.
b) A number line going from negative 4.5 to 0 in increments of 0.5. An arrow goes from negative 4.5 to negative 2 and then backwards from 0 to negative 4.5.
c) A number line going from negative 2.5 to positive 4.5 in increments of 0.5. An arrow goes from negative 2.5 to 0 and also from 0 to 4.5.
d) A number line going from negative 4.5 to positive 2.5 in increments of 0.5. An arrow goes from 2.5 to 0 and from 0 to negative 4.5.
Answers
Answer:
its A i think
Step-by-step explanation:
Hope this helps!
For field trip the school bought 47 sandwiches for $4.60 each and 39 bags of chips for $1.25 each how much was spent on sandwiches
Answers
Answer: 216.2 + 48.75 = 264.95
Step-by-step explanation:
Multiply the amount of sandwiches by the cost.
47 * 4.60 = 216.2
Multiply the amount of chips by the cost.
39 * 1.25 = 48.75
Add them the totals together.
216.2 + 48.75 = 264.95
Beginning with the equation 2x + 8y = 12, write an
additional equation that would create:
a system with infinitely many solutions.
(Hint: a system with infinitely many solutions makes
the same line)
Answers
The system has infinitely many solutions, and one of them is (9, -3/4).
To have a system of linear equations with infinitely many solutions, the two equations must represent the same line. Therefore, we need to obtain a second equation that has the same slope and y-intercept as 2x + 8y = 12.Here's how we can do that:2x + 8y = 12 is equivalent to 2(x + 4y) = 12, which reduces to x + 4y = 6.To create a second equation that represents the same line, we can multiply this equation by a constant, say 2, which gives us:2(x + 4y) = 12 (original equation)2x + 8y = 12 (distribute 2 on the left side)4x + 16y = 24 (multiply both sides by 2)Dividing both sides by 4, we get x + 4y = 6, which is the same as the first equation. Therefore, the system of equations is:2x + 8y = 124x + 16y = 24This system of equations is consistent and has infinitely many solutions because the two equations are equivalent and represent the same line, and every point on this line satisfies both equations.The solution to this system can be found using either equation by solving for one variable in terms of the other and substituting into either equation. For instance, we can solve for y in terms of x as follows:x + 4y = 6 => 4y = 6 - x => y = (6 - x)/4Substituting this expression for y into the first equation gives us:2x + 8((6 - x)/4) = 122x + 2(6 - x) = 1230 - 2x = 12 => 2x = 18 => x = 9Substituting x = 9 into y = (6 - x)/4 gives us:y = (6 - 9)/4 = -3/4Therefore, the system has infinitely many solutions, and one of them is (9, -3/4).
Learn more about Dividing here,Write a division problem with 1/4 as the dividend and 3 as the divisor. then, find the
quotient.
the answer has to be w...
https://brainly.com/question/30126004
#SPJ11
A spherical shell centered at the origin has an inner radius of 3 cm and an outer radius of 5 cm. Write an integral in spherical coordinates giving the mass of the shell (for this representation, do not reduce the domain of the integral by using symmetry; type phi and theta for \phi and \theta)
Answers
The integral for the mass of the shell becomes ∫₀^π ∫₀^{2π} ∫₃^₅ ρ(r, θ, φ) r^2 sin φ dr dθ dφ.
To find the mass of the spherical shell, we need to integrate the density over its volume. Let's assume that the density of the shell is constant, denoted by rho.
Using spherical coordinates, the integral for the mass of the shell can be written as:
M = ∫∫∫ ρ(r, θ, φ) r^2 sin φ dr dθ dφ
where,
ρ(r, θ, φ) is the density of the shell, which is assumed to be constant,
r is the radial distance from the origin,
θ is the azimuthal angle, which measures the angle in the xy-plane from the positive x-axis,
φ is the polar angle, which measures the angle from the positive z-axis.
Since the shell is centered at the origin and has an inner radius of 3 cm and an outer radius of 5 cm, the limits of integration are:
3 ≤ r ≤ 5
0 ≤ θ ≤ 2π
0 ≤ φ ≤ π
Thus, the integral for the mass of the shell becomes:
M = ∫∫∫ ρ(r, θ, φ) r^2 sin φ dr dθ dφ
= ∫₀^π ∫₀^{2π} ∫₃^₅ ρ(r, θ, φ) r^2 sin φ dr dθ dφ
the symmetry of the shell, which means that we are integrating over the entire volume of the shell. If the shell had some symmetry, we could have reduced the domain of the integral by exploiting that symmetry.
for such more question on integral
https://brainly.com/question/15282085
#SPJ11
7.) A company sells cases of candy. The revenue generated by selling x cases is described by the
function R(x) = 60x. The cost to produce the cases is described by the function C(x)
= 35x + 200. The company's profit for selling the cases of candy is the difference between the
revenue and the cost amounts. Which function describes P, the profit function?
A. P(x) = 95x + 200
B. P(x) = 25x + 200
C. P(x) = 25x - 200
D. P(x) = 95x - 200
Answers
Answer:
D
Step-by-step explanation:
please help !! Select the correct answer.
What is the circumference of this circle?

Answers
Answer:
D
Step-by-step explanation:
To find circumference, it's 2(pi)r
Twice the radius is the diameter, so it's 10/2 = 5
2*3.14*5
Since you don't multiply pi, it's 10(pi)
Answer:
D. 10π
Step-by-step explanation:
C= 2πr
r being the radius of the circle
r= d/2
= 10/2 = 5
. C= 2πr
C= 2×π×r
= 2×π×5
= 10π
What transformation is used to create this frieze pattern?
180° rotation
vertical reflection
horizontal reflection
glide reflection

Answers
Using translation concepts, it is found that the transformation used to create this frieze pattern is a 180º rotation.
What is a translation?
A translation is represented by a change in the function graph, according to operations such as multiplication or sum/subtraction in it's definition.
In this problem, looking at each pair and imagining a coordinate plane, we can see that one image is on the second quadrant and the other in the fourth, that is, the following rule is applied:
(x,y) -> (-x,-y).
Which is a 180º rotation.
More can be learned about translation concepts at https://brainly.com/question/4521517
#SPJ1
Answer:
glide reflection
Step-by-step explanation:
Can you help me solve this equation I been trying to search a video explaining this but nothing and I gaved up studying for six days and now I am trying to get back to track anyways ... The equation is a linear equation : f(x)=-x-11 with the following
1.4f(-2)+5f(1)
2.-5f(12)-2f(-9)
3. 3f(5)x f(2)
4.f(9)/f(-6)
Answers
Answer:
4 I promise
jhjhhhhjjj bug check txt TC gym c rectify txt
. (a) when is the directional derivative of f a maximum? (b) when is it a minimum? (c) when is it 0? (d) when is it half of its maximum value?
Answers
The solution of the following options is angle between the gradient and directional derivative is equal to zero and the gradient's highest value, the directional derivative is maximized..
What are directional derivative and gradient?A directional derivative shows the rate at which a function changes in any particular direction. The directional derivative may be calculated using a formula that uses the gradient. A function of more than one variable's gradient shows the direction of greatest change.
What are the applications of directional derivatives?We may determine the instantaneous rate of z change in any direction at a place using the directional derivative. These instantaneous rates of change may be used to construct planes and lines that are perpendicular to a surface at a particular location, which is the subject of the next section.
Part A:
When the angle between the gradient and directional derivative is equal to zero and the gradient's highest value, the directional derivative is maximized.
Part B:
When the angle between the directional derivative and gradient is 180 degrees, the minimal value will be reached.
Part C:
When the gradient and directional derivative are 90 degrees apart, the result will be zero.
Part D:
At an angle of 60 degrees between the gradient and the directional derivative, its maximum value will be half its maximum value.
To learn more about direction derivative, click the following link:-
https://brainly.com/question/18722002
#SPJ4
Write the letter of the correct answer on your answer sheet. If your answer is not found among
the choices, write the correct answer.
For items 1-5, refer to the graph at the right.
____1. Which of the following could be the equation of the parabola?
A. = ( − 2)2 + 1 C. = ( + 1)2 + 2
B. = ( + 2)2 + 1 D. = ( − 1)2 + 2
____2. Determine the y- intercept of the graph?
A. = −5
C. = 5
B. = −3
D. = 3
____3. What is the range of the parabola?
A. {:≥1}
C. {:≥ -1}
B. {:≤1}
D. {:≤ -1}
____4. What is the axis of symmetry of the graph?
A. x = 2
C. y = 2
B. x = 1
D. y = 1
____5. What is the vertex of the parabola?
A. (-2, -1)
C. (2, 1)
B. (-2, 1)
D. (2, -1)
____6. Describe the graph of () = −2 + 6 − 24
A. Opens to the right
C. Opens to the left
B. Opens upward
D. Opens downward
____7. What is the y-intercept of the parabola defined by the equation = ( + 2)2?
A. -4
B. -2
C. 2
D. 4
____8. What is the minimum value of the graph of the quadratic function = 2 + 4?
A. -4
B. -2
C. 2
D. 4
____9. What is the vertex of the parabola having the equation y = (x – 3)2 + 1?
A. (3, -1)
B. (-1, 3)
C. (1, 3)
D. (3, 1)
____10. What is the vertex form of the equation =2−4+7?
A. =(−2)2−3
C. =(+2)2−3
B. =(−2)2+3
D. =(+2)2+3
____11. The equation of the axis of symmetry of the function = −22 + 5 is____.
A. x = 5
C. − 4
3
B. x= -2
D. 5
4
____12. Which of the following equations of parabola has a wider opening? A. y = 1
4
2
C. y = 3x2 B. y = 1
2
2
D. y = 5x2
____13. Determine the equation of the resulting graph when the parabola with the equation
y = x2 + 3, is shifted 4 units downward.
A. y = x2 – 4
C. y = x2 + 1
B. y = x2 – 1
D. y = x2 + 7
For items 14-15, refer to the graph at the right.
____14. Which of the following could be the equation of the parabola?
A. = −2 + 5
C. = 2
2
+ 5
B. = − 2
2
= 5
D. = 2 + 5
____15. What is the vertex of the parabola?
A. V(-5, 0)
C. V(0, 5)
B. V(0, -5)
D. V(5, 0)
Answers
Answer:
Hello dear asker, you have to put the picture of the graph, then I would be happy to help
explain how to solve 5^x-2 = 8 using the change of base formula log y= log y/log b include the solution for x in your answer round your answer to the nearest tenth
Answers
The solution for x in the equation 5^(x-2) = 8 is approximately 4.8 (rounded to the nearest tenth).
To solve the equation 5^(x-2) = 8, we can use the change of base formula for logarithms. The change of base formula states that for any positive base b and positive numbers x and y, we have:
log base b of y = log base c of y / log base c of b,
where c can be any positive base except 1.
Let's apply the change of base formula to the given equation:
5^(x-2) = 8.
Taking the logarithm of both sides using the base 5, we get:
log base 5 of (5^(x-2)) = log base 5 of 8.
Applying the change of base formula with c = 5, we have:
(x - 2) = log base 5 of 8 / log base 5 of 5.
Since log base 5 of 5 is equal to 1, we can simplify the equation further:
(x - 2) = log base 5 of 8 / 1.
(x - 2) = log base 5 of 8.
Now, to isolate x, we can add 2 to both sides:
x = log base 5 of 8 + 2.
Evaluate log base 5 of 8, we find:
x ≈ 2.7712 + 2.
x ≈ 4.7712 (rounded to the nearest tenth).
The solution for x in the equation 5^(x-2) = 8 is approximately 4.8 (rounded to the nearest tenth).
For more questions on equation
https://brainly.com/question/17145398
#SPJ8
A 12-sided die is rolled. The set of equally likely outcomes is
3,4,5,6,7,8,9,10,11,12) Find the probability of rolling a number greater than 2.
Answers
The probability of rolling a number greater than 2 is 10/10 or 100%.
When rolling a 12-sided die with the set of equally likely outcomes {3, 4, 5, 6, 7, 8, 9, 10, 11, 12}, we want to find the probability of rolling a number greater than 2.
Since all the numbers in the given set are greater than 2, we can determine the probability by simply considering the ratio of the favorable outcomes to the total possible outcomes.
In this case, there are 10 favorable outcomes (3 to 12) and 10 total outcomes.
Thus, the probability of rolling a number greater than 2 is 10/10, which simplifies to 1, or 100%
. So, when rolling this specific 12-sided die, you have a 100% chance of rolling a number greater than 2.
Learn more about probability at https://brainly.com/question/16484393
#SPJ11
A survey of 100 high school students provided this frequency table on how students get to school: Grade Drive to School Take the bus Walk Sophomore 2 25 3 Junior 13 20 2 25 5 5 Senior What is the probability that a randomly selected student does NOT drive to school? ? P(Drive to school) Remember to reduce your answer.

Answers
Probability that the student doesn't drive to school is (3/5) .
What does a probability simple definition entail?
A probability is a number that expresses the possibility or likelihood that a specific event will take place. Both proportions between 0 and 1 and percentages between 0% and 100% can be used to describe probabilities.
Total students = 100
Total students who drive to school = 2 + 13 + 25 = 40
Probability ( Drive to school ) = (40/100)
Probability ( Not drive to school ) = 1 - (40/100)
Probability ( Not drive to school ) = (60/100) = (3/5)
Hence, probability that the student doesn't drive to school is (3/5) .
Learn more about Probability
brainly.com/question/30034780
#SPJ1
the area of one lateral face of a right pyramid with an equilateral triangular base is 75 square meters. if the slant height is 30 meters, what is the length of the side of its base, in meters?
Answers
A right pyramid with an equilateral triangular base has a lateral face with a surface area of 75 square meters. The side of the base of a slant with a height of 30 meters is 5 meters long.
Let’s call the side length of the equilateral triangular base “s”. We know that the area of one lateral face is 75 square meters, and that face is a triangle with base s and height 30 meters (the slant height). We can use the formula for the area of a triangle to solve for s:
Area = (1/2) * base * height
75 = (1/2) * s * 30
Simplifying the equation, we get:
75 = 15s
s = 75/15
s = 5
Therefore, the length of the side of the equilateral triangular base is 5 meters.
To learn more about equilateral triangular base, refer:-
https://brainly.com/question/29193261
#SPJ4
What is the first step to solving ?3(x-1)=15-6x
A. Add 15
B.distribute 3 into the parenthesis
C. Subtract
Answers
Answer:
distribute 3 into the parenthesis
Find the lateral area of the cone in terms of pi.

Answers
To find the lateral area of a cone, use this formula:
\(\pi r\sqrt{h^2+r^2}\)
where r is the radius (in this case, 11) and h is the height (in this case, 26)
Try plugging the values in. If you need additional help, feel free to ask!
Find The Critical Points Of The Function F(X,Y)=X2+Y2−6x−8y. B) Using The Lagrange Multipliers Method Find
Answers
The critical points of the function f(x, y) = x^2 + y^2 - 6x - 8y are (3, 4).
To find the critical points of the function f(x, y) = x^2 + y^2 - 6x - 8y, we need to find the points where the gradient of the function is equal to zero.
Step 1: Find the partial derivatives of f(x, y) with respect to x and y:
∂f/∂x = 2x - 6
∂f/∂y = 2y - 8
Step 2: Set the partial derivatives equal to zero and solve for x and y:
2x - 6 = 0
2y - 8 = 0
Solving these equations, we find:
x = 3
y = 4
Therefore, the critical point of the function f(x, y) is (3, 4).
Now, using the Lagrange multipliers method, we can find the constrained critical points.
Let's say we have a constraint g(x, y) = k, where k is a constant. In this case, we don't have a specific constraint given, so we can skip this step.
Step 1: Set up the Lagrangian function L(x, y, λ) = f(x, y) - λ(g(x, y) - k). Since we don't have a constraint, we can set L(x, y, λ) = f(x, y).
L(x, y) = x^2 + y^2 - 6x - 8y
Step 2: Find the partial derivatives of L(x, y) with respect to x, y, and λ:
∂L/∂x = 2x - 6
∂L/∂y = 2y - 8
Step 3: Set the partial derivatives equal to zero and solve for x, y, and λ:
2x - 6 = 0
2y - 8 = 0
Solving these equations, we get:
x = 3
y = 4
Therefore, the critical point of the function f(x, y) using the Lagrange multipliers method is also (3, 4).
In summary, the critical points of the function f(x, y) = x^2 + y^2 - 6x - 8y are (3, 4).
Learn more about functions from
https://brainly.com/question/11624077
#SPJ11
A tortoise and hare start from rest and have a race. As the race begins, both accelerate forward. The hare accelerates uniformly at a rate of 1 m/s
2
for 4.8 seconds. It then continues at a constant speed for 12 seconds, before getting tired and slowing down with constant acceleration coming to rest 85 meters from where it started. The tortoise accelerates uniformly for the entire distance, finally catching the hare just as the hare comes to a stop. 4) What is the acceleration of the hare once it begins to slow down? See solution m/s
2
You currently have 3 submissions for this question. Only 12 submission are allowed. You can make 9 more submissions for this question. 5) What is the total time the hare is moving? See solution 5 6) What is the acceleration of the tortoise? See solution m/s
2
Answers
The acceleration of the hare, once it begins to slow down, is \($\frac{-11.52 - 12v_{\text{hare2}} + 85}{6}$\)\(m/s$^2$\), the total time the hare is moving in \($4.8 + 12 + t_{\text{hare3}}$\) seconds, and the acceleration of the tortoise \(($a_{\text{tortoise}}$)\) is to be determined.
To solve the problem in detail:
Hare's initial acceleration \(($a_{\text{hare1}}$) = 1 m/s$^2$\)
Hare's acceleration after constant speed \(($a_{\text{hare2}}$) = ?\) (to be determined)
Hare's time of constant speed \(($t_{\text{hare2}}$) = 12 s\)
Hare's final displacement \(($s_{\text{hare}}$) = 85 m\)
Step 1: Finding the hare's acceleration once it begins to slow down.
Using the equation of motion, we can determine the acceleration:
\(\[s_{\text{hare}} = v_{\text{hare1}} \cdot t_{\text{hare1}} + \frac{1}{2} \cdot a_{\text{hare1}} \cdot t_{\text{hare1}}^2 + v_{\text{hare2}} \cdot t_{\text{hare2}} + \frac{1}{2} \cdot a_{\text{hare2}} \cdot t_{\text{hare2}}^2\) \\\(85 = 0 + \frac{1}{2} \cdot 1 \cdot (4.8)^2 + v_{\text{hare2}} \cdot 12 + \frac{1}{2} \cdot a_{\text{hare2}} \cdot (12)^2\]\)
Solving for \($a_{\text{hare2}}$\), we get:
\(\[a_{\text{hare2}} = \frac{-11.52 - 12v_{\text{hare2}} + 85}{6}\]\)
Step 2: Finding the total time the hare is moving.
The total time the hare is moving is the sum of the time for acceleration \(($t_{\text{hare1}}$)\), time at a constant speed \(($t_{\text{hare2}}$)\), and the time to decelerate to rest \(($t_{\text{hare3}}$)\):
\(\[t_{\text{total hare}} = t_{\text{hare1}} + t_{\text{hare2}} + t_{\text{hare3}}\]\)
\(\[t_{\text{total hare}} = 4.8 + 12 + t_{\text{hare3}}\]\)
Step 3: Finding the acceleration of the tortoise.
The tortoise accelerates uniformly for the entire distance, so its acceleration \(($a_{\text{tortoise}}$)\) is constant.
Therefore:
The acceleration of the hare, once it begins to slow down, is \($\frac{-11.52 - 12v_{\text{hare2}} + 85}{6}$\)\(m/s$^2$\).The total time the hare is moving is in \($4.8 + 12 + t_{\text{hare3}}$\) seconds.The acceleration of the tortoise \(($a_{\text{tortoise}}$)\) is to be determined.Learn more about acceleration: https://brainly.com/question/25876659
#SPJ11
