which is another way to wite the product of 18 x 6
Answers
Answer: 108
Step-by-step explanation: we find the product of 18 and 6 by simply calculating 18 times 6 which equals 108.
Answer:
18
x
6
=108
Step-by-step explanation:
Related Questions
HELP SOME1 HELP!! PLEASE!!!!!!!!!! HELPPPPPP


Answers
Answer: Archie I think
Step-by-step explanation: Brainliest please?
Name the types of angles and solve for x.130042x +4These areX

Answers
The angles are opposite angles. Opposite angles are equal:
Hence, it is mathematically represented as:
42x + 4 = 130
Subtract 4 from both sides, we have:
42x + 4 - 4 = 130 - 4
42x = 126
Divide both sides by 42 to get x, we have:
x = 3
What is the radius and diameter of the following circle? 7 cm Diameter = - Answer: Radius = Diameter =
Answers
Answer:
7cm in diameter, 3.5 in radius
Step-by-step explanation:
What is the area of a circle with a radius of 4 inches? Use 3.14 for π. Enter your answer as a decimal in the box.
enter your answer
in²
Answers
Answer:
A≈ 50.27in^2
Step-by-step explanation:
A= πr^2=
π·4^2≈ 50.26548
the equation for the area of a circle is:
A = pi(r)^2
plugging in 4 for r, you get 50.24

What is the name of this shape?

Answers
Answer:
octagon
Hope it helps
I am sure about this
The work shows how to use long division to find?

Answers
Answer:
remainder = \(\frac{1}{x-2}\)
Step-by-step explanation:
The remainder is the value of the subtraction of the last 2 lines in the procedure.
5x - 9
- (5x - 10)
That is
5x - 5x = 0 and - 9 - (- 10) = - 9 + 10 = 1
over the divisor x- 2 , gives
remainder = \(\frac{1}{x-2}\)
811570 rounded to nearest hundred thousand
Answers
Answer:
800,000
Step-by-step explanation:
8 is in the hundred thousands, 1 is in the ten thousands, 1 is in the thousands, 5 is in the hundreds, 7 is in the tens, 0 is in the ones place
It rounds down as its nowhere near 900,000 which changes all its digits.
3
\(3 \sqrt{81} \)
what's the answer
Answers
Answer will be 27.
Given,
3√81
Now, to solve the expression the squares of whole numbers and square roots for some numbers must be known.
For example, squares of
1² = 1
2² = 4
3² = 9
4² = 16
5² = 25
6² = 36
7² = 49
8² = 64
9² = 81
10² = 100
Square roots,
√100 = 10
√81 = 9
√64 = 8
√49 = 7
√36 = 6
√25 = 5
√16 = 4
√9 = 3
√4 = 2
√1 = 1
Now ,
3√81 = 3× 9
= 27.
Thus the value is 27.
Know more about Square roots,
https://brainly.com/question/16113248
#SPJ1
Find the third side in simplest radical form:

Answers
Answer:
√130Step-by-step explanation:
Using Pythagorean theorem to find the third side
√9²+7² = √81+49=√130Answer:
\(\sqrt{130}\)
Step-by-step explanation:
since the triangle is a right triangle
we can use the Pythagorean theorem to find the hypotenuse
let a=7, b=9, c= ?c² = 7² + 9²c = \(\sqrt{130}\)Find the volume of the rectangular prism. Please help will mark brainlist
A. 194 m3
B. 388 m3
C. 140 m3
D. 280 m3

Answers
Answer:
\( {280m}^{3} \)
Answer:
D. 280 m³
Step-by-step explanation:
The formula for the volume of a cuboid is length × width × height
v = 20 m × 7 m × 2 m = 280 m³
Unless specified, all approximating rectangles are assumed to have the same width. Evaluate the upper and lower sums for f(x) = 2 + sin(x), 0 ≤ x ≤ with n = 8.
Answers
The top and lower sums for n =2,4, and 8 and f(x) = 2 +sin(x),0 x are as follows:
n = 2: Upper Sum = 7.85398; Lower sum ≈ 7.85398
n = 4: Upper sum ≈ 6.43917; Lower sum ≈ 6.43917
n = 8: Upper sum ≈ 6.35258; Lower sum ≈ 6.352
It is necessary to first divide the range [0, ] into n subintervals of identical width x, where x = ( - 0)/n = /n, in order to calculate the upper and lower sums for the equations f(x) = 2 + sin(x), 0 x for n = 2, 4, and 8. The endpoints of these subintervals are:
x0 = 0, x1 = Δx, x2 = 2Δx, ..., xn-1 = (n-1)Δx, xn = π.
Then, for each subinterval [xi-1, xi], we can approximate the area under the curve by the area of a rectangle whose height is either the maximum or minimum value of f(x) on that interval. The sum of these areas' overall subintervals gives us the upper and lower sums.
For n = 2:
Subintervals: [0, π/2], [π/2, π]Width of subintervals: Δx = π/2Maximum values of f(x) on each subinterval:[0, π/2]: f(π/2) = 2 + sin(π/2) = 3
[π/2, π]: f(π) = 2 + sin(π) = 2
Minimum values of f(x) on each subinterval:[0, π/2]: f(0) = 2 + sin(0) = 2
[π/2, π]: f(π/2) = 2 + sin(π/2) = 3
Upper sum: (3)(π/2) + (2)(π/2) = 5π/2 ≈ 7.85398Lower sum: (2)(π/2) + (3)(π/2) = 5π/2 ≈ 7.85398For n = 4:
Subintervals: [0, π/4], [π/4, π/2], [π/2, 3π/4], [3π/4, π]Width of subintervals: Δx = π/4Maximum values of f(x) on each subinterval:[0, π/4]: f(π/4) = 2 + sin(π/4) ≈ 2.70711
[π/4, π/2]: f(π/2) = 2 + sin(π/2) = 3
[π/2, 3π/4]: f(3π/4) = 2 + sin(3π/4) ≈ 2.29289
[3π/4, π]: f(π) = 2 + sin(π) = 2
Minimum values of f(x) on each subinterval:[0, π/4]: f(0) = 2 + sin(0) = 2
[π/4, π/2]: f(π/4) = 2 + sin(π/4) ≈ 2.70711
[π/2, 3π/4]: f(π/2) = 2 + sin(π/2) = 3
[3π/4, π]: f(3π/4) = 2 + sin(3π/4) ≈ 2.29289
Upper sum: (2.70711 + 3 + 2.29289)(π/4) ≈ 6.43917Lower sum: (2 + 2.70711 + 3 + 2.29289)(π/4) ≈ 6.43917For n = 8:
Subintervals: [0, π/8], [π/8, π/4], [π/4, 3π/8], [3π/8, π/2], [π/2, 5π/8], [5π/8, 3π/4], [3π/4, 7π/8], [7π/8, π]Width of subintervals: Δx = π/8Maximum values of f(x) on each subinterval:[0, π/8]: f(π/8) = 2 + sin(π/8) ≈ 2.25882
[π/8, π/4]: f(π/4) = 2 + sin(π/4) ≈ 2.70711
[π/4, 3π/8]: f(3π/8) = 2 + sin(3π/8) ≈ 2.96593
[3π/8, π/2]: f(π/2) = 2 + sin(π/2) = 3
[π/2, 5π/8]: f(5π/8) = 2 + sin(5π/8) ≈ 2.96593
[5π/8, 3π/4]: f(3π/4) = 2 + sin(3π/4) ≈ 2.70711
[3π/4, 7π/8]: f(7π/8) = 2 + sin(7π/8) ≈ 2.25882
[7π/8, π]: f(π) = 2 + sin(π) = 2
Minimum values of f(x) on each subinterval:[0, π/8]: f(0) = 2 + sin(0) = 2
[π/8, π/4]: f(π/8) = 2 + sin(π/8) ≈ 2.25882
[π/4, 3π/8]: f(π/4) = 2 + sin(π/4) ≈ 2.70711
[3π/8, π/2]: f(3π/8) = 2 + sin(3π/8) ≈ 2.96593
[π/2, 5π/8]: f(π/2) = 2 + sin(π/2) = 3
[5π/8, 3π/4]: f(5π/8) = 2 + sin(5π/8) ≈ 2.96593
[3π/4, 7π/8]: f(3π/4) = 2 + sin(3π/4) ≈ 2.70711
[7π/8, π]: f(7π/8) = 2 + sin(7π/8) ≈ 2.25882
Upper sum: (2.25882 + 2.70711 + 2.96593 + 3 + 2.96593 + 2.70711 + 2.25882 + 2)(π/8) ≈ 6.35258Lower sum: (2 + 2.25882 + 2.70711 + 2.96593 + 3 + 2.96593 + 2.70711 + 2.25882)(π/8) ≈ 6.352The complete question is:-
Unless specified, all approximating rectangles are assumed to have the same width. Evaluate the upper and lower sums for f(x) = 2 + sin(x),0 ≤ x ≤ π with n = 2, 4, and 8.
To learn more about the upper sum, refer:-
https://brainly.com/question/29636891
#SPJ1
Which of the following equations is the best model for a line of fit for the data?
ŷ = −1.34x + 21.5
ŷ = 1.34x + 21.5
ŷ = −0.75x + 17
ŷ = 0.75x + 17

Answers
The correct option is (a) ŷ = -1.34x+21.5 , that is the best model to fit the scatter plot.
What is Scatter plot?A scatter plot (or scatter chart, scatter graph) uses dots to represent values for two(2) different numeric variables. The position of each dot on horizontal and vertical axis indicates values for an individual data point.
The model of the equation best for the plot is,
ŷ = -1.34x+21.5
At point (1,20),
ŷ = -1.34x+21.5
20 = (-1.34 × 1) + 21.5
20 ≈ 20.15
At point (3,19),
ŷ = -1.34x+21.5
19 = (-1.34 × 3) + 21.5
19 ≈17.45
At point (5,15),
ŷ = -1.34x+21.5
15 = (-1.34 × 5) + 21.5
15 ≈ 14.75
The model ŷ = -1.34x+21.5 is giving the best estimation.
To learn more about Scatter plot, visit:
brainly.com/question/29231735
#SPJ1
Which of the following shows the image T of triangle ABC under the transformation (x,y)→(x−4,y+1)?
Answers
The required image T of triangle ABC under the transformation (x,y) → (x-4, y+1) is formed by connecting the vertices A'(a-4, b+1), B'(c-4, d+1), and C'(e-4, f+1)
To find the image T of triangle ABC under the transformation (x,y) → (x-4, y+1), apply this transformation to each of the vertices of triangle ABC and then connect the new vertices to form the image T.
Let's assume that the coordinates of the vertices of triangle ABC are A(a,b), B(c,d), and C(e,f).
To find the image of vertex A under the transformation, we substitute x = a and y = b into the transformation equation:
(x,y) → (x-4, y+1)
(a,b) → (a-4, b+1)
Therefore, the image of vertex A is A'(a-4, b+1).
Similarly, we can find the images of vertices B and C:
B'(c-4, d+1)
C'(e-4, f+1)
Therefore, the image T of triangle ABC under the transformation (x,y) → (x-4, y+1) is formed by connecting the vertices A'(a-4, b+1), B'(c-4, d+1), and C'(e-4, f+1)
Learn more about transformation here:
https://brainly.com/question/27143173
#SPJ1
Replace a and b with the correct values

Answers
Answer:
tan(25) = 12/x
I'm sorry, don't know what a and b are, if they refer to the fraction, then 12 should be at the top and x should be at the bottom
Step-by-step explanation:
Using SOHCAHTOA, we have,
tan(25) = 12/x
Which interval notation represents the set of all numbers from 5 to 12, inclusive? O (5,12) O [5,12 Submit Answer O [5, 12) O (5,12
Answers
By definition, there are the following intervals in Interval notation:
1. A Closed interval: It includes its endpoints. To write it, you must use brackets []
2. An Open interval: It does not include its endpoints, to write it you must use parentheses ().
For this case, since you need to find the set of all numbers from 5 to 12, inclusive, you must write this as a Closed interval, because it includes the endpoints 5 and 12.
Therefore, knowing the above, you can write the set of all numbers from 5 to 12 inclusive, in Interval notation. Then, the answer is the following:
\(\lbrack5,12\rbrack\)At one point the average price of regular unleaded gasoline was $3.39 per gallon. Assume that the standard deviation price per gallon is $ per gallon and use Chebyshev's inequality to answer the following. (a) What percentage of gasoline stations had prices within standard deviations of the mean? (b) What percentage of gasoline stations had prices within standard deviations of the mean? What are the gasoline prices that are within standard deviations of the mean? (c) What is the minimum percentage of gasoline stations that had prices between $ and $?
Answers
This question was not written completely
Complete Question
At one point the average price of regular unleaded gasoline was $3.39 per gallon. Assume that the standard deviation price per gallon is $0.07 per gallon and use Chebyshev's inequality to answer the following.
(a) What percentage of gasoline stations had prices within 3 standard deviations of the mean?
(b) What percentage of gasoline stations had prices within 2.5 standard deviations of the mean? What are the gasoline prices that are within 2.5 standard deviations of the mean?
(c) What is the minimum percentage of gasoline stations that had prices between $3.11 and $3.67?
Answer:
a) 88.89% lies with 3 standard deviations of the mean
b) i) 84% lies within 2.5 standard deviations of the mean
ii) the gasoline prices that are within 2.5 standard deviations of the mean is $3.215 and $3.565
c) 93.75%
Step-by-step explanation:
Chebyshev's theorem is shown below.
1) Chebyshev's theorem states for any k > 1, at least 1-1/k² of the data lies within k standard deviations of the mean.
As stated, the value of k must be greater than 1.
2) At least 75% or 3/4 of the data for a set of numbers lies within 2 standard deviations of the mean. The number could be greater.μ - 2σ and μ + 2σ.
3) At least 88.89% or 8/9 of a data set lies within 3 standard deviations of the mean.μ - 3σ and μ + 3σ.
4) At least 93.75% of a data set lies within 4 standard deviations of the mean.μ - 4σ and μ + 4σ.
(a) What percentage of gasoline stations had prices within 3 standard deviations of the mean?
We solve using the first rule of the theorem
1) Chebyshev's theorem states for any k > 1, at least 1-1/k² of the data lies within k standard deviations of the mean.
As stated, the value of k must be greater than 1.
Hence, k = 3
1 - 1/k²
= 1 - 1/3²
= 1 - 1/9
= 9 - 1/ 9
= 8/9
Therefore, the percentage of gasoline stations had prices within 3 standard deviations of the mean is 88.89%
(b) What percentage of gasoline stations had prices within 2.5 standard deviations of the mean?
We solve using the first rule of the theorem
1) Chebyshev's theorem states for any k > 1, at least 1-1/k² of the data lies within k standard deviations of the mean.
As stated, the value of k must be greater than 1.
Hence, k = 3
1 - 1/k²
= 1 - 1/2.5²
= 1 - 1/6.25
= 6.25 - 1/ 6.25
= 5.25/6.25
We convert to percentage
= 5.25/6.25 × 100%
= 0.84 × 100%
= 84 %
Therefore, the percentage of gasoline stations had prices within 2.5 standard deviations of the mean is 84%
What are the gasoline prices that are within 2.5 standard deviations of the mean?
We have from the question, the mean =$3.39
Standard deviation = 0.07
μ - 2.5σ
$3.39 - 2.5 × 0.07
= $3.215
μ + 2.5σ
$3.39 + 2.5 × 0.07
= $3.565
Therefore, the gasoline prices that are within 2.5 standard deviations of the mean is $3.215 and $3.565
(c) What is the minimum percentage of gasoline stations that had prices between $3.11 and $3.67?
the mean =$3.39
Standard deviation = 0.07
Applying the 2nd rule
2) At least 75% or 3/4 of the data for a set of numbers lies within 2 standard deviations of the mean. The number could be greater.μ - 2σ and μ + 2σ.
the mean =$3.39
Standard deviation = 0.07
μ - 2σ and μ + 2σ.
$3.39 - 2 × 0.07 = $3.25
$3.39 + 2× 0.07 = $3.53
Applying the third rule
3) At least 88.89% or 8/9 of a data set lies within 3 standard deviations of the mean.μ - 3σ and μ + 3σ.
$3.39 - 3 × 0.07 = $3.18
$3.39 + 3 × 0.07 = $3.6
Applying the 4th rule
4) At least 93.75% of a data set lies within 4 standard deviations of the mean.μ - 4σ and μ + 4σ.
$3.39 - 4 × 0.07 = $3.11
$3.39 + 4 × 0.07 = $3.67
Therefore, from the above calculation we can see that the minimum percentage of gasoline stations that had prices between $3.11 and $3.67 corresponds to at least 93.75% of a data set because it lies within 4 standard deviations of the mean.
Find the area of the shaded part

Answers
The area of the composite figure is 111 square units.
Describe Composite Figure?A composite figure is a 2D shape or figure that is made up of two or more simpler shapes or figures combined together. These simpler shapes can be any combination of polygons, circles, or other curves.
Composite figures are often formed when two or more basic shapes are put together to create a more complex shape. For example, a figure that consists of a rectangle and a triangle placed together is a composite figure.
To find the area of a composite figure like this, we can break it up into simpler shapes and then find the area of each shape and add them together.
First, we can see that the shape consists of three triangles and a rectangle:
Triangle 1: (0,3), (2,3), (2,7)
Triangle 2: (-7,7), (-7,6), (5,-6)
Triangle 3: (5,1), (-1,-2), (-5,2)
Rectangle: (-3,5), (0,3), (-7,7), (-7,6)
To find the area of each triangle, we can use the formula:
Area = 1/2 * base * height
For Triangle 1, the base is 2 - 0 = 2 and the height is 7 - 3 = 4. So the area is:
Area of Triangle 1 = 1/2 * 2 * 4 = 4
For Triangle 2, the base is 5 - (-7) = 12 and the height is 7 - (-6) = 13. So the area is:
Area of Triangle 2 = 1/2 * 12 * 13 = 78
For Triangle 3, we can see that it is a right triangle with sides of length 6, 6, and 8. So the area is:
Area of Triangle 3 = 1/2 * 6 * 8 = 24
To find the area of the rectangle, we can use the formula:
Area = length * width
The length is the distance between (-7,7) and (-7,6), which is 1. The width is the distance between (-7,7) and (-3,5), which is 5. So the area is:
Area of Rectangle = 1 * 5 = 5
Finally, we can add up the areas of all the shapes to get the total area:
Total Area = Area of Triangle 1 + Area of Triangle 2 + Area of Triangle 3 + Area of Rectangle
Total Area = 4 + 78 + 24 + 5
Total Area = 111 square units
Therefore, the area of the composite figure is 111 square units.
To know more about triangle visit:
https://brainly.com/question/27937129
#SPJ1
Can someone pls help me with this I’ll mark brainliest

Answers
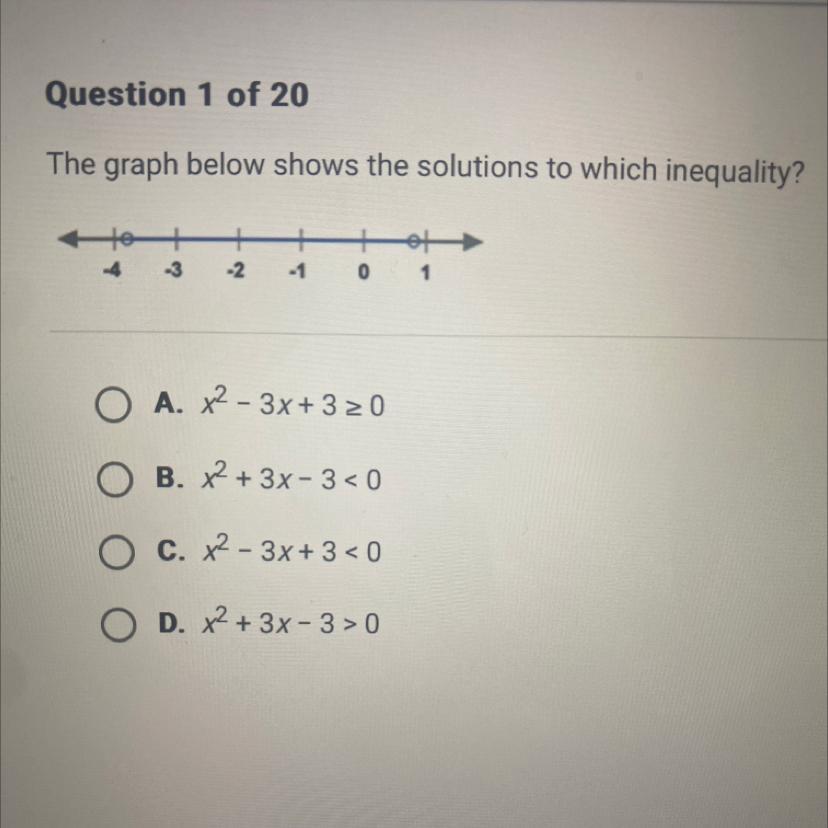
The graph below shows the solutions to which inequality?
A. x^2-3x+3 ≥0
B. x² + 3x-3 <0
C. x²-3x+3<0
D. x² + 3x-3>0
Answers
The inequality expression that corresponds to the solution of the inequality graph is x² + 3x - 3 < 0.
option B.
What is the solution of the inequality?The inequality expression that corresponds to the solution of the inequality graph is determined by simplifying the equations as follows;
The solution of the graph,
x > -4 and x < 1
The first equation with "≥" is ruled out because the graph doesn't have a thick dot.
Let's simplify the second expression;
x² + 3x - 3 < 0
solve using quadratic formula;
x > -3.79 or x < 0.79
The third expression is ruled out since its solution will be complex.
For the last expression;
x² + 3x - 3 > 0
x < -3.79 or x > 0.79
Thus, the correct inequality expression is x² + 3x - 3 < 0.
Learn more about inequality expression here: https://brainly.com/question/25275758
#SPJ1
find the equation of a line perpendicular to 2x + 2y= -10 that passes through the point (6,2)
Answers
Answer: The equation of a line perpendicular to 2x + 2y = - 10 that passes through the point (6, 2) is y = x - 4
Find the following sums ( for letter C)

Answers
Each number in the sum is even, so we can remove a factor of 2.
2 + 4 + 6 + 8 + ... + 78 + 80 = 2 (1 + 2 + 3 + 4 + ... + 39 + 40)
Use whatever technique you used in (a) and (b) to compute the sum
1 + 2 + 3 + 4 + ... + 39 + 40
With Gauss's method, for instance, we have
S = 1 + 2 + 3 + ... + 38 + 39 + 40
S = 40 + 39 + 38 + ... + 3 + 2 + 1
2S = (1 + 40) + (2 + 39) + ... + (39 + 2) + (40 + 1) = 40×41
S = 20×21 = 420
Then the sum you want is 2×420 = 840.
Directions: Calculate the volume of each of the following prisms.

Answers
The volumes of the prisms are :- 1) 11760 units³, 2) 7938 units³, 3) 9261 units³, 4) 22800 unit³, 5) 11781 units³, 6) 38936 units³, 7) 23125 units³, 8) 26208 units³ and 9) 14688 units³
What are prisms?A prism is a solid shape that is bound on all its sides by plane faces.
Given are prisms, we need to find their volumes :-
Volume = area of base × height
1) Base is a rectangle, area = length × width, height = 24
Volume = 24·14·35 = 11760 units³
2) Base is a rectangle, area = length × width, height = 21
Volume = 21·14·27 = 7938 units³
3) This is a cube, with side 21 units
Volume of cube = side³ = 9261 units³
4) This is a trapezoidal prism,
Volume = 1/2(b1+b2) × height × length = 1/2(36+24) × 38 × 20
= 22800 unit³
5) This is a triangular prism,
Volume = 1/2 × height × length × base
= 1/2 × 33 × 34 × 21 = 11781 units³
6) This is a cylinder,
Base is circular, volume = π·radius²·height
= 3.14·20·20·31 = 38936 units³
7) Base is a rectangle, area = length × width, height = 37
Volume = 25·37·25 = 23125 units³
8) Base is a rectangle, area = length × width, height = 28
Volume = 39·24·28 = 26208 units³
9) Base is a rectangle, area = length × width, height = 36
Volume = 36·24·17 = 14688 units³
Hence, the volumes of the prisms are :- 1) 11760 units³, 2) 7938 units³, 3) 9261 units³, 4) 22800 unit³, 5) 11781 units³, 6) 38936 units³, 7) 23125 units³, 8) 26208 units³ and 9) 14688 units³
Learn more about prisms, click;
https://brainly.com/question/29722724
#SPJ9
Smallest successive composites with gap
17, 73, 2, 19
Answers
Answer:
Well, the smallest successive composites with gap 17, 73, 2, and 19 would have to be:
1. $341 = 11 \times 31$
2. $458 = 2 \times 299$
3. $460 = 2^2 \times 5 \times 23$
4. $479 = 13 \times 37$
8x - 6y = -20
-16х +7 y = 30
Answers
Answer:
8x - 6y = 20-16х +7 y = 30
Step-by-step explanation:
Answer:
(-1,2)
Step-by-step explanation:
multiply top equation by 2 and add them together as follows
16x-12y=-40
-16x+7y=30
-5y=-10
y=2
now replace y with 2 in the first equation and solve for x
8x-6(2)=-20
8x-12=-20
8x=-8
x=-1
What is the equation of a line that has a slope of 2 and passes through the point (4,6) ?
Answers
Answer:
\(y-6=2\,(x-4)\)
or in slope y-intercept form :
\(y=2x-2\)
Step-by-step explanation:
The easiest way of find the answer for this is to use what is called the "point-slope" form of a line, because you are in fact given the value of the slope (m) and also a point \((x_0,y_0)\) it goes through:
\(y-y_0=m\,(x-x_0)\)
In our case the equation becomes:
\(y-y_0=m\,(x-x_0)\\y-6=2\,(x-4)\\\)
This can also be written in the slope-intercept form by solving for "y" and operating to remove the parenthesis:
\(y-6=2\,(x-4)\\y=2x-8+6\\y=2x-2\)
Because Earth's rotation is gradually slowing, the length of each day increases: The day at the end of 1.0 century is 1.0 ms longer than the day at the start of the century. In 24 centuries, what is the total of the daily increases in time (that is, the sum of the gain on the first day, the gain on the second day, etc.)
Answers
Answer:
14.6 minutes
Step-by-step explanation:
Since there is a 1 ms increase per day and there are 365 days a year, the time increase per year is 1 ms/day × 365 days/year = 365 ms/year.
So, in 24 centuries, there are 24 × 1 century = 24 × 100 years = 2400 years (since 1 century = 100 years)
So, the total of the daily increase in time in 24 centuries is time increase per year × 24 centuries
= 365 ms/year × 2400 years
= 876000 ms
= 876 s
= 876 s/60s
= 14.6 minutes
Anne wants to make a scale drawing of her house with the drawing showing a ratio 1 inch to 12 feet.
If Anne's house is 84 feet long, how long, in inches, should her scale drawing be?
Answers
7 in
\( \frac{1}{2} = \frac{x}{84} \\ 84 \times \frac{1}{12} = \frac{x}{84} \times 84 \\ 84 \times \ \frac{1}{12} = x \\ 7 = x\)
Evaluate when x = -3 and y= -1: A. -4 B. -3 C. 0 D. -6
Answers
Answer:
The anwser is B. -3 Hope This Helps!
Step-by-step explanation:
Answer:
The Guy Above Me Is Wrong, It's Not B.
Step-by-step explanation:
I Think It's Actually A.
In ΔHIJ,
m
∠
H
=
(
3
x
+
12
)
∘
m∠H=(3x+12)
∘
,
m
∠
I
=
(
5
x
+
9
)
∘
m∠I=(5x+9)
∘
, and
m
∠
J
=
(
2
x
+
9
)
∘
m∠J=(2x+9)
∘
. Find
m
∠
I
.
m∠I
Answers
Answer:
i try my best to find the answer if i can
Step-by-step explanation:
Need help the questions is in thos picture thank you !!

Answers
Answer:
\(-\frac{3}{4}\)
Step-by-step explanation:
Substitute the values
(-4)+ (-2)/ 8
-6/ 8
Simplify by 2 (a common factor)
-6/2 = -3
8/2 =4