Which inequality is represented by this graph?
A. y-< -1/3 x+1
B. y-> -1/3 x+1
C. y> -1/3 x+1
D. y< -1/3 x+1

Answers
Answer:
A y<= -1/3x+1
Step-by-step explanation:
Related Questions
HELP ME ASAP!!!!!!!!!
Please help
See picture attached.
WINNER GETS THANKS, A STAR RATING-EXCELLENT AND BRAINLIEST!!!!!!!!!! Good Luck!
Happy Easter!
apokibunnyavatar

Answers
Answer:
23,26,29,32,35,38,41,44
Step-by-step explanation:
In mathematics, WHOLE NUMBERS are the basic counting numbers 0, 1, 2, 3, 4, 5, 6, … and so on. Whole numbers are the real numbers which includes zero and all the positive integers. Whole numbers don't include negative numbers, fractions, or decimals.
Simplify 5(8d+ 6
A. 13d + 6
B. 130d+ 11
C. 40d+ 6
D. 40d+ 30
Answers
Answer:
The answer choice is D.
Step-by-step explanation:
Multiply 5 and 8
= 40
Then put d to 40
=40d
And also multiply 6 with 5
which equals to 30.
Now the expression would be: 40d + 30
Polynomial Regression: Method of Least Squares My Solutions Problem Description: Read Chapter 15, "General Linear Least-Squares and Nonlinear Regression," from Chapra's textbook and watch/review Lecture 11. Using the same approach as was employed to derive Eqs. (14.15) and (14.16), derive the least-squares fit of the following model: y = a1*x + a2*x^2 That Is, determine the coefficients that result in the least-squares fit for a second-order polynomlal with a zero Intercept.
Answers
To derive the least-squares fit for the model y = a1x + a2x^2 with a zero intercept, we need to minimize the sum of squared residuals. Let's denote the observed data points as (xi, yi) for i = 1 to n.
The objective is to find the values of a1 and a2 that minimize the following sum of squared residuals:
SSR = ∑(yi - (a1xi + a2xi^2))^2
To find the minimum, we differentiate SSR with respect to a1 and a2 separately and set the derivatives equal to zero.
Partial derivative with respect to a1:
∂SSR/∂a1 = -2∑(yi - (a1xi + a2xi^2))*xi = 0
Partial derivative with respect to a2:
∂SSR/∂a2 = -2∑(yi - (a1xi + a2xi^2))*xi^2 = 0
Expanding the above equations:
∑(yixi) - a1∑(xi^2) - a2∑(xi^3) = 0 ------ (1)
∑(yixi^2) - a1∑(xi^3) - a2∑(xi^4) = 0 ------ (2)
Now, let's solve these equations to find the values of a1 and a2.
From equation (1):
a1∑(xi^2) + a2∑(xi^3) = ∑(yi*xi) ------ (3)
From equation (2):
a1∑(xi^3) + a2∑(xi^4) = ∑(yi*xi^2) ------ (4)
We can express equations (3) and (4) in matrix form as:
| ∑(xi^2) ∑(xi^3) | | a1 | = | ∑(yixi) |
| ∑(xi^3) ∑(xi^4) | | a2 | = | ∑(yixi^2) |
Solving this system of linear equations will give us the values of a1 and a2.
Once a1 and a2 are determined, we have the least-squares fit of the model y = a1x + a2x^2 with a zero intercept.
Know more about least-squares here:
https://brainly.com/question/29834077
#SPJ11
Use the original price and the markdown to find the retail price.
Original price: $70; Markdown: 34%
Answers
How large should we choose n so that the trapezoid-rule approximation, Tn, to the integral sin r dz is accurate to within 0.00001? (Use the error bound given in Section 5.9 of the course text.)
Answers
The trapezoidal rule is a numerical integration method that uses trapezoids to estimate the area under a curve. The trapezoidal rule can be used for both definite and indefinite integrals. The trapezoidal rule approximation, Tn, to the integral sin r dz is given by:
Tn = (b-a)/2n[f(a) + 2f(a+h) + 2f(a+2h) + ... + 2f(b-h) + f(b)]where h = (b-a)/n. To determine how large n should be so that Tn is accurate to within 0.00001, we can use the error bound given in Section 5.9 of the course text. According to the error bound, the error, E, in the trapezoidal rule approximation is given by:E ≤ ((b-a)³/12n²)max|f''(x)|where f''(x) is the second derivative of f(x). For the integral sin r dz, the second derivative is f''(r) = -sin r. Since the absolute value of sin r is less than or equal to 1, we have:max|f''(r)| = 1.
Substituting this value into the error bound equation gives:E ≤ ((b-a)³/12n²)So we want to choose n so that E ≤ 0.00001. Substituting E and the given values into the inequality gives:((b-a)³/12n²) ≤ 0.00001Simplifying this expression gives:n² ≥ ((b-a)³/(0.00001)(12))n² ≥ (b-a)³/0.00012n ≥ √(b-a)³/0.00012Now we just need to substitute the values of a and b into this expression. Since we don't know the upper limit of integration, we can use the fact that sin r is bounded by -1 and 1 to get an upper bound for the integral.
For example, we could use the interval [0, pi/2], which contains one full period of sin r. Then we have:a = 0b = pi/2Plugging in these values gives:n ≥ √(pi/2)³/0.00012n ≥ 5073.31Since n must be an integer, we round up to the nearest integer to get:n = 5074Therefore, we should choose n to be 5074 so that the trapezoidal rule approximation, Tn, to the integral sin r dz is accurate to within 0.00001.
To know more about integration visit :
https://brainly.com/question/31744185
#SPJ11
__________ typically are used to display continuous measures.
Answers
Histograms typically are used to display continuous measures.
The histograms typically are used to display continuous measures.
Charts TypesThere are different types of charts: histogram, line chart, pie chart, and others.
The histogram is a type of chart used as a tool that provides a way to assess the distribution of data. From this type of chart, a set of data are previously tabulated and divided into classes. In the other words, the histogram is applied to summarize discrete or continuous measures, so it becomes more easily the understand the used data. There are many websites and software that allow the plot of this type of chart.
From the explanation, it is possible to identify the histograms typically are used to display continuous measures.
Read more about the histogram here:
https://brainly.com/question/13652813
#SPJ12
(951² - 159²)÷(7539²-357²) x (258²-852²)
Answers
Answer:
(879,120)÷(56709072) ×(-659340)=-10221.274
Step-by-step explanation:
we use bedmas rules when it comes to long solving questions.
Consider a utility function that represents preferences over perfect complements: (1,2)=min{341,172}u(x1,x2)=min{34x1,17x2}.
Answers
According to the question, the utility function can be written as: \(U(x,y)=min(341,172)\)
What is utility function and perfect complements?
A utility function is a standard rule which is assigned to all consumption bundles. And it is represented as two good models which are known as domain and codomain. It is also used to represent the individual items for the goods or services beyond their monetary value. Similarly, when two goods are consumed perfectly then they are called perfect complements.
Similarly, Perfect complement is: \(max(341,172)\)
Therefore, the equations can be written for the points(1,2):
\(x_{1} +2x_{2} =172\) and \(x_{1} +x_{2} = 341\)
And the calculated equation is perfect complements:
\(x_{1} +2x_{2} =172\) and \(x_{1} +x_{2} = 341\)
To learn more about the utility function and perfect complement from the given link:
https://brainly.com/question/13684345
#SPJ4
1. NEATLY SHOW ALL OF YOUR WORK as you find an expression for the EXACT value for sin 75° by using... ( a) ...a sum or difference formula. b) a half-angle formula (note 75⁰ is half of 1500).
Answers
(a) Sum or difference formula: sin 75 = (√3 + 1)√2 / 4.
(b) Half-angle formula: sin 75 = √(3/2) / 2.
Explanation:
Given that 75 degrees is half of 150 degrees. We need to find the value of sin 75 degrees using the sum or difference formula and half-angle formula.
a) Sum or difference formula: The given formula is used to find the sum of the sine function. It is given as follows: sin (A + B) = sin A cos B + cos A sin B. If A = 45 and B = 30 degrees, we can use the values of cos 30 degrees = √3 / 2, cos 45 degrees = 1/ √2, sin 30 degrees = 1/2, and sin 45 degrees = 1/ √2.
By substituting these values in the formula, we get sin (A + B) = sin A cos B + cos A sin B as sin (45 + 30) = sin 45 cos 30 + cos 45 sin 30. On simplifying this equation, we get sin 75 = (1/√2)(√3/2) + (1/√2)(1/2).
Further simplifying this equation, we get sin 75 = (√3 + 1) / 2√2. Finally, on rationalizing the denominator of this equation, we get sin 75 = (√3 + 1)√2 / 4.
b) Half-angle formula:The half-angle formula of sine function is given as;
sin x/2 = ± √(1 – cos x) / 2
Let x = 150 degrees. Then, cos 150 = - 1/2 and sin 150 = 1/2
Now substituting the given values in the formula;
sin 75 = ± √(1 – (- 1/2)) / 2
sin 75 = ± √(3/2) / 2
Now, as 75 degrees is in the first quadrant, the value of sine is positive. Hence;
sin 75 = √(3/2) / 2.
Therefore, the exact value of sin 75 degrees by using the sum or difference formula is (√3 + 1)√2 / 4 and by using the half-angle formula is √(3/2) / 2.
Know more about Half-angle formula here:
https://brainly.com/question/30400810
#SPJ11
given that the absolute value of the difference of the two roots of $ax^2 + 5x - 3 = 0$ is $\frac{\sqrt{61}}{3}$, and $a$ is positive, what is the value of $a$?
Answers
The value of "a" is approximately 1.83 given that the absolute value of the difference of the two roots of the quadratic equation "ax squared plus 5x minus 3 equals 0" is the square root of 61 divided by 3, and "a" is positive.
We are given that the absolute value of the difference between the two roots of the quadratic equation "ax squared plus 5x minus 3 equals 0" is the square root of 61 divided by 3, and "a" is positive. We need to find the value of "a".
Let the two roots of the equation be r1 and r2, where r1 is not equal to r2. Then, we have:
|r1 - r2| = √(61) / 3
The sum of the roots of the quadratic equation is given by r1 + r2 = -5 / a, and the product of the roots is given by r1 × r2 = -3 / a.
We can express the difference between the roots in terms of the sum and product of the roots as follows:
r1 - r2 = √((r1 + r2)² - 4r1r2)
Substituting the expressions we obtained earlier, we have:
r1 - r2 = √(((-5 / a)²) + (4 × (3 / a)))
Simplifying, we get:
r1 - r2 = √((25 / a²) + (12 / a))
Taking the absolute value of both sides, we get:
|r1 - r2| = √((25 / a²) + (12 / a))
Comparing this with the given expression |r1 - r2| = √(61) / 3, we get:
√((25 / a²) + (12 / a)) = √(61) / 3
Squaring both sides and simplifying, we get:
25 / a² + 12 / a - 61 / 9 = 0
Multiplying both sides by 9a², we get:
225 + 108a - 61a² = 0
Solving this quadratic equation for "a", we get:
a = (108 + √(108² + 4 × 61 × 225)) / (2 × 61)
Since "a" must be positive, we take the positive root:
a = (108 + √(108² + 4 × 61 × 225)) / (2 × 61) ≈ 1.83
Therefore, the value of "a" is approximately 1.83.
Learn more about absolute value at
https://brainly.com/question/1301718
#SPJ4
The question is -
Given that the absolute value of the difference of the two roots of the quadratic equation "ax squared plus 5x minus 3 equals 0" is the square root of 61 divided by 3, and "a" is positive, what is the value of "a"?
a company's revenue from selling x units of an item is given as dollars. if sales are increasing at the rate of 70 per day, find how rapidly revenue is growing (in dollars per day) when 420 units have been sold.
Answers
The rate of growth of revenue when 420 units have been sold is R'(420) = R'(350)..
Revenue from selling x units = R(x). Also, sales are increasing at a rate of 70 per day. That means if x units are sold today, then tomorrow, the units sold would be (x + 70) units. Rate of increasing sales = 70 per day. Now, when 420 units have been sold:
Initial units sold = x = 420 - 70 = 350 units
Total units sold = 420 units
Number of units sold today = 420 - 350 = 70 units
Now, Revenue generated from 350 units of the item = R(350)
Revenue generated from 420 units of the item = R(420)
Rate of growth of revenue when 420 units have been sold = R'(420)\
From the definition of the derivative:
R'(x) = lim_ {h→0} {R(x+h) - R(x)}/{h}
R'(420) = lim_ {h→0} {R(420+h) - R(420)}/{h}
R(420) = R(350 + 70) = R(350) + R'(350) * (70)And, R(420 + h)
= R(350 + 70 + h) = R(350) + R'(350) * (70 + h), Using these equations,
R'(420) = lim_ {h→0} {R(350) + R'(350) * (70 + h) - R(350) - R'(350) * (70)}/{h}
= lim_ {h→0} {R'(350) * h}/{h}
= R'(350)
Thus, the rate of growth of revenue when 420 units have been sold is R'(420) = R'(350).
To learn more about rate of growth refer :
https://brainly.com/question/14263843
#SPJ11
What’s the answer to this?!!!!

Answers
Yes, it is a right triangle.
Answer:
Yes
Step-by-step explanation:
Yehvsbsgwbdhgjebwjosnwks
Please do number 12 for me.

Answers
Answer:
72
Step-by-step explanation:
24x + 21x + 15x =180
60x= 180
x=3
Largest angle =24x
=24*3=72
Answer:
72
Step-by-step explanation:
15x + 21x +24x = 180 (Angle sum property of a triangle.)
60x = 180
x = 3
hence largest angle = 72
when training a classifier, it is common to split the available data into a training set, a hold-out set, and a test set, each of which has a different role. which data set is used to learn the conditional probabilities?
Answers
When training a classifier, the training set is used to learn the conditional probabilities.
The training set is used to learn the conditional probabilities because the training set is used to train the classifier on the patterns and features in the data, which in turn helps the classifier to learn the conditional probabilities of the different classes in the data.
The hold-out set and test set are used to evaluate the performance of the classifier and ensure that it is not overfitting to the training set.
By evaluating the classifier on data that it has not seen before, we can get a more accurate estimate of its true performance and the probability of correctly classifying new data.
To learn more about conditional probabilities visit : https://brainly.com/question/23382435
#SPJ11
suppose you take a standardized test and you are in the 12 th percentile. what does this percentile mean?you scored 12% lower than the class average12% of the scores were higher than your score12% of the scores were your score or loweryou scored 12% higher than the class average
Answers
The percentile rank of 12 means that you scored higher than 12% of the test-takers who took the same exam, and lower than the other 88%.
Percentile is a statistical measure used to compare an individual's score with the rest of the population. For example, if your score is in the 12th percentile, it means that you performed better than only 12% of the people who took the same test, while the other 88% of test-takers scored higher than you.
Percentile rank is a useful tool for comparing an individual's performance with the larger population, as it provides a clear understanding of where a person stands in comparison to others who took the same exam. It can also be used to monitor one's progress over time, and to identify areas where improvement is needed.
For more questions like Ranks visit the link below:
https://brainly.com/question/29754859
#SPJ11
Leroux health insurance is considering changing the options in one of their health care plans (plan a) based on customer feedback that prescriptions and regular visits to the doctor are too expensive for the insured individual. How can leroux reduce the costs of regular health care without driving up the price of their health care plan? leroux health insurance plan a cost: monthly premium: $248. 00 annual deductible: $5,500. 00 co-pays: brand-name prescriptions $35. 00 generic prescriptions $15. 00 visits: primary care physician: $40. 00 specialist: $60. 00 urgent care: $125. 00 emergency room: $325. 00 a. Reduce the monthly premium but increase the co-pay amounts to compensate for the lower premium. B. Reduce the annual deductible, but increase the co-pay amounts so that the monthly premium can stay the same. C. Reduce the co-pay amounts but increase the annual deductible so that the monthly premium can stay the same. D. Reduce the co-pay amounts but increase the monthly premium to compensate for the lower deductible.
Answers
Leroux can reduce the costs of regular health care without driving up the price of their health acre plan by : (c) Reducing the co-pay amounts but increase the annual deductible so that the monthly premium can stay the same.
Since the customers are complaining that the cost of regular visits and prescriptions ($15) are too expensive for them based on the plan they choose, this means that the purpose of the health insurance plan which is to reduce the overwhelming cost burden on individuals when trying to access proper healthcare is not be implemented successfully.
The co-pay amount which is usually known as the out-of-pocket amount that insurers pay whenever they go for regular doctor visits ( covered service in the insurance package ) and reducing this amount will reduce the immediate cost which makes the customers to complain about how expensive assessing a doctor on regular visits are.
The effect of the increased annual deductible is one way to push the immediate burden of paying a higher co-pay amount by the customer.
Learn more about healthcare:
https://brainly.com/question/28426089
#SPJ4
a website asks visitors to vote for which of several user-submitted videos is funniest. after a few days they have collected 250 votes, and they would like to construct a 95% confidence interval for the proportion of visitors who prefer one of the videos. however, they recognize that their sampling method involves voluntary response, so the data may be biased. how can they compensate for this problem when constructing their confidence interval?
Answers
Collect 250 or more more votes using an SRS.
You must carefully consider how you will choose a sample that is representative of the group as a whole if you want to make accurate conclusions from your data. It is referred to as a sampling method. You can use one of the following two main sampling techniques in your study:
Random selection is a key component of probability sampling, which enables you to draw robust statistical conclusions about the entire group.
Non-probability sampling entails non-random selection based on practicality or other factors, making it simple to gather data.
A simple random sample, also known as an SRS, is a subset of people (also known as a sample) picked at random from a larger group of people (also known as a population) with an equal probability. It is a method of choosing a sample at random.
explanation :
As everyone is aware, inferential statistics has the property of objectivity, which means that a statistic is an objective estimator of a population parameter. The confidence intervals adhere to this characteristic as well. Our sample mean is used in the computation of our confidence interval since we believe that the genuine population mean is somewhat close to it.
Confidence interval typically accounts for random error; relatively little systematic error is accounted for (i.e, bias). If we expand the sample size, we can eventually lower the bias in the confidence interval. Bias becomes zero when n equals infinity.
Therefore, employing an SRS to collect 250 more votes or more would be necessary to offset the issue.
To know more about sampling visit: brainly.com/question/13287171
#SPJ4
alguien me ayuda ,, Hallar la suma de los primeros 20 numeros multiples de 3
Answers
Answer:
630
Step-by-step explanation:
1st = 3
2nd = 6
3rd = 9 ...
20th = 60
Súmalos todos juntos para encontrar la suma.
3 + 6 + 9 + 12 + 15 + 18 + 21 + 24 + 27 + 30 + 33 + 36 + 39 + 42 + 45 + 48 + 51 + 54 + 57 + 60 = 630
La suma de los primeros 20 múltiplos de 3 es 630
¡Espero que esto ayude!
set up, but do not evaluate, an integral for the volume of the solid obtained by rotating the region bounded by the given curves about the specified line.
Answers
This integral represents the sum of the volumes of all the infinitesimally thin cylindrical shells that make up the solid.
To set up the integral for the volume of the solid obtained by rotating the region bounded by the curves y = x, y = 0, and x = 4 about the line x = 8, we can use the method of cylindrical shells.
First, let's draw a rough sketch of the region and the axis of rotation:
```
|
|
| +-----------+
| | |
| | |
| | |
| | |
| +-----------+ <-- x = 4
| |
| |
| |
| |
| |
| |
| |
| |
+------------------------ <-- x = 8
```
The region bounded by y = x, y = 0, and x = 4 is a triangle with a right angle at the origin.
To set up the integral, we consider an infinitesimally thin cylindrical shell with radius r, height h, and thickness Δy. The volume of this shell can be approximated as the product of its circumference, height, and thickness.
The radius of the shell, r, is the distance from the axis of rotation (x = 8) to the curve y = x. Since x = y for the region, r = 8 - y.
The height of the shell, h, is the difference between the x-values at the top and bottom of the region. In this case, h = 4 - 0 = 4.
The thickness of the shell, Δy, represents an infinitesimally small change in the y-direction.
Therefore, the volume of the shell is approximately given by V_shell = 2πr * h * Δy.
To find the total volume, we integrate this expression over the range of y-values that span the region. In this case, the integral is set up as follows:
∫[0, 4] 2π(8 - y) * 4 * dy
This integral represents the sum of the volumes of all the infinitesimally thin cylindrical shells that make up the solid. By evaluating this integral, you can find the exact volume of the solid obtained by rotating the region bounded by y = x, y = 0, and x = 4 about the line x = 8.
Learn more about integral here:
https://brainly.com/question/31109342
#SPJ11
Set up, but do not evaluate, an integral for the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. y = x, y = 0, X = 4; about x = 8 2 (8 - y2)2 – 16 dy 0
Assume that the recovery time for an individual from an infectious disease can be modeled as a normal distribution. (a) Calculate the time, d, in days for an individual to recover from being initially infected, with a 95% confidence level, assuming that the likelihood of recovering at any time is modeled as a normal distribution with a mean of 5 days and a standard deviation of 0.5 days. (b) Use the SIR model that you constructed previously. Assume that a city of 10 million people is confronted with a potential infectious epidemic. A ship arrives at the international airport carrying 100 individuals who are infected, but are unaware that they are infected. While contagious, infected individuals come into transmission contact with another individual once every 2 days. The recovery process is modeled using the Poisson process from Part (a). Assume that recovered individuals that survive develop immunity to the disease. Plot the fraction of susceptible individuals, infected individuals, and recovered individuals as a function of time throughout the epidemic. (c) What fraction of the total population will have ultimately come down with the infectious disease once the epidemic is over? How many days after the ship docking did this number finally reach steady state (i.e.,the epidemic is completely over). (d) What is the basis for this structured model (i.e.,scale, time, etc.)? What is/are the major assumptions associated with the structure?
Answers
Upper
daysThe(a) The time for an individual to recover from an infectious disease, is estimated to be between 4.02 and 5.98 days. (d) The structured SIR model assumes homogeneous mixing, constant population, recovered immunity.
(a) To calculate the time for an individual to recover with a 95% confidence level, we can use the properties of the normal distribution. The 95% confidence interval corresponds to approximately 1.96 standard deviations from the mean in both directions.
Given:
Mean (μ) = 5 days
Standard deviation (σ) = 0.5 days
The confidence interval can be calculated as follows:
Lower limit = Mean - (1.96 * Standard deviation)
Upper limit = Mean + (1.96 * Standard deviation)
Lower limit = 5 - (1.96 * 0.5)
= 5 - 0.98
= 4.02 days
Upper limit = 5 + (1.96 * 0.5)
= 5 + 0.98
= 5.98 days
Therefore, the time for an individual to recover from the infectious disease with a 95% confidence level is between approximately 4.02 and 5.98 days.
(b) To simulate the epidemic using the SIR model, we need additional information about the transmission rate and the duration of infectivity.
(c) Without the transmission rate and duration of infectivity, we cannot determine the fraction of the total population that will have come down with the infectious disease once the epidemic is over.
(d) The structured model in this case is the SIR (Susceptible-Infectious-Recovered) model, which is commonly used to study the dynamics of infectious diseases. The major assumptions associated with the SIR model include:
Homogeneous mixing: The model assumes that individuals in the population mix randomly, and each individual has an equal probability of coming into contact with any other individual.
Constant population: The model assumes a constant population size, without accounting for birth, death, or migration rates.
Recovered individuals develop immunity: The model assumes that individuals who recover from the infectious disease gain permanent immunity and cannot be reinfected.
No vaccination or intervention: The basic SIR model does not incorporate vaccination or other intervention measures.
These assumptions simplify the model and allow for mathematical analysis of disease spread dynamics. However, they may not fully capture the complexities of real-world scenarios, and more sophisticated models can be developed to address specific contexts and factors.
Learn more about Normal distribution here: brainly.com/question/15103234
#SPJ11
Identify which value represents the sample mean and which value represents the claimed population mean. American households spent an average of about $52 in 2007 on Halloween merchandise such as costumes, decorations and candy. To see if this number had changed, researchers conducted a new survey in 2008 before industry numbers were reported. The survey included 1, 500 households and found that average Halloween spending was $58 per household. The sample mean is dollars, while the claimed population mean is dollars. The average GPA of students in 2001 at a private university was 3.37. A survey on a sample of 203 students from this university yielded an average GPA of 3.59 in Spring semester of 2012. The sample mean is and the claimed population mean is
Answers
It is stated that the population mean is 3.37, which represents the average GPA of all students at the university in that year.
In the given scenarios:
American households' Halloween spending:
Sample Mean: $58 per household
Claimed Population Mean: $52
In this case, the sample mean represents the average spending per household obtained from the survey conducted in 2008 on 1,500 households. This sample mean is $58. It is a representative value calculated from the data collected in the sample of households.
On the other hand, the claimed population mean refers to the average spending per household in the entire population of American households. In this case, it is claimed or known that the population mean is $52, which represents the average Halloween spending in 2007.
The researchers conducted the survey in 2008 to determine if there was any change in Halloween spending compared to the claimed population mean of $52.
Average GPA of students at a private university:
Sample Mean: 3.59
Claimed Population Mean: 3.37
Here, the sample mean is the average GPA calculated from the data collected in the survey on a sample of 203 students from the university in the spring semester of 2012. The sample mean is 3.59, representing the average GPA of the sampled students.
The claimed population mean, on the other hand, refers to the average GPA of all students at the private university in 2001. It is stated that the population mean is 3.37, which represents the average GPA of all students at the university in that year.
The survey conducted in 2012 aimed to determine if there was any change in the average GPA compared to the claimed population mean of 3.37 in 2001.
To know more about average refer here:
https://brainly.com/question/897199#
#SPJ11
A manufacturer's sales price per part (P) can be calculated by: P= 250+16.25N/n
Where P= minimum sales price per part, $250 is the overhead costs, $16.25 is the cost of producing the part, and N= number of parts produced. Find the number of parts that must be produced to make the sales price $30, rounded to the nearest part.
Answers
The number of parts that must be produced to make the sales price $30 is 55 parts
Given, the manufacturer's sales price per part (P) can be calculated by:P= 250+16.25N/nWhere P= minimum sales price per part, $250 is the overhead costs, $16.25 is the cost of producing the part, and N= number of parts produced. We have to find the number of parts that must be produced to make the sales price $30, rounded to the nearest part.To find the number of parts (N) that must be produced to make the sales price $30:Put the given values in the given equation:P = 250 + 16.25N/NSubstitute P = 30 in the above equation.30 = 250 + 16.25N/NSimplify and rearrange the above equation to find N.16.25N = 30N - 750-13.75N = -750N = -750/-13.75N = 54.545Then, rounding to the nearest whole number, the number of parts that must be produced to make the sales price $30 is 55 parts (nearest whole number).Therefore, 55 parts must be produced to make the sales price $30 (rounded to the nearest part).
Learn more about number :
https://brainly.com/question/10547079
#SPJ11
when a test for steroids is given to soccer players, 93% of the players taking steroids test positive and 12% of the players not taking steroids test positive. suppose that 5% of soccer players take steroids. what is the probability that a soccer player who tests positive takes steroids? (enter the value of the probability in decimal format and round the final answer to three decimal places.)'
Answers
The probability that a soccer player who tests positive takes steroids is approximately 0.279 or 27.9%.
To solve this problem, we can use Bayes' theorem:
P(Steroids|Positive) = P(Positive|Steroids) * P(Steroids) / P(Positive)
where:
P(Steroids|Positive) = probability of taking steroids given a positive test result
P(Positive|Steroids) = probability of testing positive given that the player takes steroids (93%)
P(Steroids) = probability of a soccer player taking steroids (5%)
P(Positive) = overall probability of testing positive (calculated below)
To calculate P(Positive), we need to use the law of total probability:
P(Positive) = P(Positive|Steroids) * P(Steroids) + P(Positive|No Steroids) * P(No Steroids)
where:
P(Positive|No Steroids) = probability of testing positive given that the player does not take steroids (12%)
P(No Steroids) = probability of a soccer player not taking steroids (100% - 5% = 95%)
Plugging in the values, we get:
P(Positive) = 0.93 * 0.05 + 0.12 * 0.95 = 0.1165
Now we can calculate P(Steroids|Positive):
P(Steroids|Positive) = 0.93 * 0.05 / 0.1165 = 0.398
Therefore, the probability that a soccer player who tests positive takes steroids is 0.398 (rounded to three decimal places).
To find the probability that a soccer player who tests positive takes steroids, we can use Bayes' Theorem:
P(A|B) = (P(B|A) * P(A)) / P(B)
Here, let A be the event "player takes steroids" and B be the event "player tests positive."
We are given:
- P(B|A) = 0.93 (93% of players taking steroids test positive)
- P(A) = 0.05 (5% of soccer players take steroids)
- P(B|A') = 0.12 (12% of players not taking steroids test positive)
To find P(B), we can use the Law of Total Probability:
P(B) = P(B|A) * P(A) + P(B|A') * P(A')
Since P(A') = 1 - P(A) = 1 - 0.05 = 0.95, we have:
P(B) = (0.93 * 0.05) + (0.12 * 0.95)
Now, we can use Bayes' Theorem to find P(A|B):
P(A|B) = (0.93 * 0.05) / ((0.93 * 0.05) + (0.12 * 0.95))
P(A|B) ≈ 0.279
Therefore, the probability that a soccer player who tests positive takes steroids is approximately 0.279 or 27.9%.
To learn more about probability, click here:
brainly.com/question/30034780
#SPJ11
Ally sold 18 boxes of Girl Scout cookies this was 20% the number of boxes that Kayla sold. How many boxes did Kayla sell
Answers
Answer:
reverse percentage
20% = 18
find 1% by dividing both sides by 20
1%= 0.9
find 100% by multiplying both sides by 100.
100%=90
Answer:
qwertyuiop;lkjhtrgfdvxfwre2324567890-[098765432wedfghjkl/., cxsder6789p;
Step-by-step explanation:
hgfwxhjhgffmbjhtfbvnhghfbnhgfnvngkjhjyt
A small country emits 150,000 kilotons of carbon dioxide per year. In a recent global
agreement, the country agreed to eut its carbon emissions by 5.4% per year for the
next 14 years. In the first year of the agreement, the country will keep its emissions at
150,000 kilotons and the emissions will decrease 5.4% in each successive year. How
many total kilotons of carbon dioxide would the country emit over the course of the
14 year period, to the nearest whole number?
Answers
how would you move the green shape exactly over the gray shape using the fewest moves? check only necessary moves
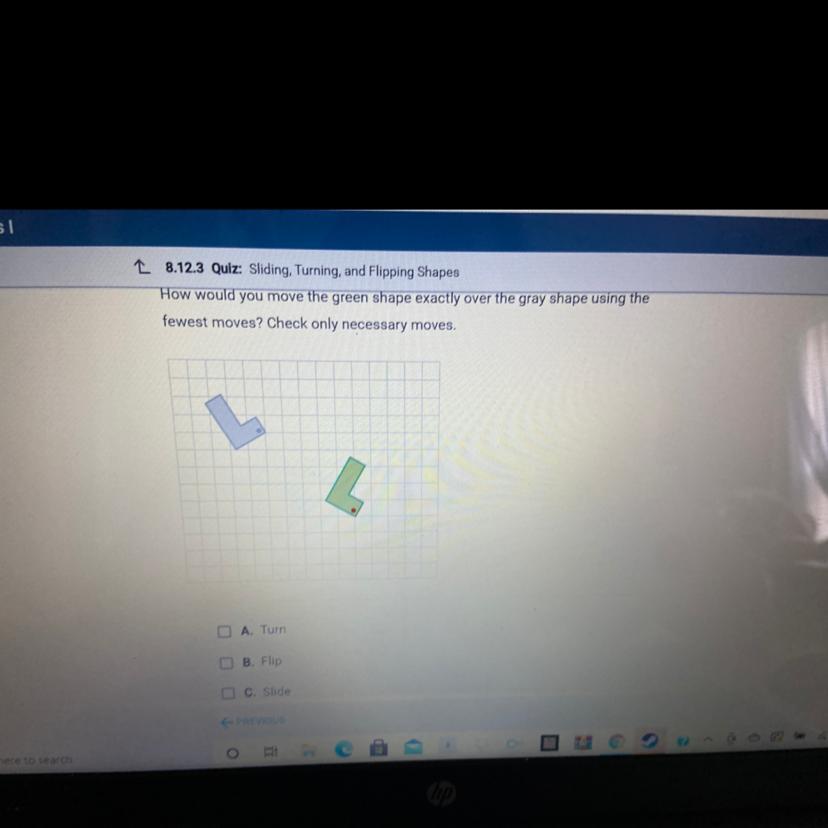
Answers
Answer:
turn and rotate
Step-by-step explanation:
Answer:
Flip then slide
Step-by-step explanation:
I think if you flip the shape it will go the direction of the blue shape then you just need to slide it
Determine the 4th order Newton's divided-difference interpolating polynomial for the function below. Use x=1,4,5,6,8. Find the f(x) value at x=7 and x=9. f(x)=ln(x) clear; clc; close all; Hint: we already solved for a third order polynomial. Now you just heed to follow the pattern and create a 4th order. This means you will have 4 first divided differences, 3 second divided differences, 2 theird divided differences, and 1 fourth divided differences.
Answers
To find the 4th order Newton's divided-difference interpolating polynomial for f(x)=ln(x) with x=1,4,5,6,8, we first need to calculate the divided differences:
A. (a) The 4th order Newton's divided-difference interpolating polynomial for the function f(x) = ln(x) using the given data points is:
P(x) = ln(1) + (x - 1)[(ln(4) - ln(1))/(4 - 1)] + (x - 1)(x - 4)[(ln(5) - ln(4))/(5 - 4)(5 - 1)] + (x - 1)(x - 4)(x - 5)[(ln(6) - ln(5))/(6 - 5)(6 - 1)] + (x - 1)(x - 4)(x - 5)(x - 6)[(ln(8) - ln(6))/(8 - 6)(8 - 1)]
B. (a) To find f(x) at x = 7 and x = 9 using the interpolating polynomial, substitute the respective values into the polynomial expression P(x) obtained in the previous part.
Explanation:
A. (a) The 4th order Newton's divided-difference interpolating polynomial can be constructed using the divided-difference formula and the given data points. In this case, we have five data points: (1, ln(1)), (4, ln(4)), (5, ln(5)), (6, ln(6)), and (8, ln(8)). We apply the formula to calculate the polynomial.
B. (a) To find the value of f(x) at x = 7 and x = 9, we substitute these values into the polynomial P(x) obtained in the previous part. For x = 7, substitute 7 into P(x) and evaluate the expression. Similarly, for x = 9, substitute 9 into P(x) and evaluate the expression.
Learn more about polynomial
brainly.com/question/11536910
#SPJ11
Let us suppose the following profit function for this industry: π(p,w
1
,w
2
)=
8(w
1
+w
2
)
1/2
p
2
where p is the market price of its output, while w
1
and w
2
are the prices of the inputs. Assume further that the firms are identical and that each firm faces the same market prices for both its output as well as inputs. a) Explain whether the firm is operating in the short run or long run and further determine the supply function for each firm. b) Derive the firm's input demand functions, determine their degree of homogeneity as well as the impact of a change in the input prices. c) Derive the market supply function given that there are 40 firms operating in this, market. d) If the market price of output (p) is 5 , the market price of the input (w
1
) is 1 , that of (w
2
) is also 1 and the demand function is given by q=1500/p(p+1). Determine the total market supply.
Answers
(a) The firm is operating in the long run, and its supply function is determined by the profit maximization condition.
(b) The firm's input demand functions can be derived from the profit function, and their degree of homogeneity is 1/2. Changes in input prices will impact the firm's input demand.
(c) The market supply function can be derived by aggregating the supply functions of all 40 firms operating in the market.
(d) Given the market conditions and demand function, the total market supply can be calculated.
(a) The firm is operating in the long run because it has the flexibility to adjust its inputs and make decisions based on market conditions. The firm's supply function is determined by maximizing its profit, which is achieved by setting the marginal cost equal to the market price. In this case, the supply function for each firm can be derived by taking the derivative of the profit function with respect to the price of output (p).
(b) The input demand functions for the firm can be derived by maximizing the profit function with respect to each input price. The degree of homogeneity of the input demand functions can be determined by examining the exponents of the input prices. In this case, the degree of homogeneity is 1/2. Changes in the input prices will affect the firm's input demand as it adjusts its input quantities to maximize profit.
(c) The market supply function can be derived by aggregating the individual supply functions of all firms in the market. Since there are 40 identical firms, the market supply function can be obtained by multiplying the supply function of a single firm by the total number of firms (40).
(d) To determine the total market supply, we substitute the given market conditions and demand function into the market supply function. By solving for the market quantity at a given market price, we can calculate the total market supply.
In conclusion, the firm is operating in the long run, and its supply function is determined by profit maximization. The input demand functions have a degree of homogeneity of 1/2, and changes in input prices impact the firm's input demand. The market supply function is derived by aggregating the individual firm supply functions, and the total market supply can be calculated using the given market conditions and demand function.
Learn more about market supply here:
https://brainly.com/question/13486321
#SPJ11
I need help with this

Answers
a) Since the triangles are congruent, and ΔABC is congruent to ΔDEF, segments AB and DE have the same value. Therefore, you can use algebra to solve for x when using the knowledge that (12 - 4x) is equal to (15 - 3x).
To solve:
12 - 4x = 15 - 3x
12 = 15 + x
-3 = x
Therefore, x is equal to -3.
b) To find the value of AB, plug in the value of x found in part a).
12 - 4x
12 - 4(-3)
12 - (-12)
12 + 12 = 24
Thus, segment AB is equal to 24.
c) As shown in part b), plug in the value of x found in part a) to find the value of segment DE.
15 - 3x
15 - 3(-3)
15 - (-9)
15 + 9 = 24
Thus, segment DE is also equal to 24.
We can confirm the knowledge of the equal side lengths because the triangle are congruent. This means that all the side lengths in the triangle are the same, which is confirmed when algebraically plugging in the value of x to solve for the values of the segments AB and DE.
I hope this helps!
y=-x/3 -3/2 on a graph
Answers
From the equation the slope is -1/3 and the y-intercept is -3/2. This shows that the intercept must pass through the y-axis at -3/2.
Equation of a lineA line is defined as the shortest distance between two points. The formula for finding the equation of a line in slope-intercept form is given as;
y = mx + b
The point sloe form of the equation is given as y-y1 = m(x-x1)
where
m is the slopeb is the intercept(x1, y1) is any point on the lineGiven the equation of graph to plot
y=-x/3 -3/2
From the equation the slope is -1/3 and the y-intercept is -3/2. This shows that the intercept must pass through the y-axis at -3/2.
Learn more on equation of a line here: https://brainly.com/question/18831322
#SPJ1
