Answers

Related Questions
A rare disease exists with which only 1 in 500 is affected. A test for the disease exists, but of course it is not infallible. A correct positive result (patient actually has the disease) occurs 95% of the time, while a false positive result (patient does not have the disease) occurs 1% of the time. If a randomly selected individual is tested and the result is positive, what is the probability that the individual has the disease?
Answers
Answer:
The probability that the individual has the disease is 1/500
Step-by-step explanation:
i found the fraction of 1 in 500 which is 1/500, hope this helps :)
A box has 15 candies in it: 9 are butterscotch, 2 are taffy, and 4 are caramel. (Each candy falls into only one of these categories.) Charmaine wants to select two candies to eat for dessert. The first candy will be selected at random, and then the second candy will be selected at random from the remaining candies. What is the probability that the first candy selected is butterscotch and the second candy is taffy? Do not round your intermediate computations. Round your final answer to three decimal places. (If necessary, consult a list of formulas.)
Answers
The probability that the first candy selected is butterscotch and the second candy is taffy can be calculated as the product of the probabilities of these two events occurring.
First, let's calculate the probability of selecting a butterscotch candy as the first candy. There are 9 butterscotch candies out of a total of 15 candies, so the probability is 9/15.Next, for the second candy to be taffy, we need to consider that one butterscotch candy has already been selected and removed from the box. Therefore, there are 14 candies remaining in the box, including 2 taffy candies. Hence, the probability of selecting a taffy candy as the second candy is 2/14.
To find the probability of both events occurring, we multiply the probabilities together: (9/15) * (2/14) = 18/210.Simplifying this fraction, we get 3/35.Therefore, the probability that the first candy selected is butterscotch and the second candy is taffy is 3/35, which is approximately 0.086 or rounded to three decimal places.
To learn more about probability click here : brainly.com/question/31828911
#SPJ11
f(x) = x2 – 4x – 21.
Answers
Answer:
f(x)=1
Step-by-step explanation:
Factor - 3 out of
-9x + 12
plz help
Answers
Answer:
3x - 4
Step-by-step explanation:
-9x + 12
divide by -3
3x + (-4)
3x - 4
-9 ÷ -3 = 3
12 ÷ -3 = -4
Hope this helps!
Have a nice day!
If you find my answer helpful
Pls consider marking my answer as Brainliest! It would mean a lot!
A scale drawing for an apartment is shown below.
In the drawing, 4cm represents 5m .
Assuming the bedroom is rectangular, find the area of the real bedroom.
Answers
Area of the real bedroom will be 50 m².
What is area Area of Rectangle?
A rectangle's area (A) is calculated by multiplying its length ('a') by its breadth ('b').
Area of Rectangle = (a x b).
In the drawing,
4cm represents 5m. So, 8cm represents 10m
And we have to assume that bedroom is rectangular,
Using formula of Area of Rectangle,
Area of the real bedroom = 5*10
= 50 m².
Hence, Area of the real bedroom will be 50 m².
To learn more about Area of Rectangle visit,
https://brainly.com/question/25292087
#SPJ1
PLS HELP AND EXPLAIN ESP IF YOU KNOW TRIG ILL GIVE BRAINLIEST IF POSSIBLE!!!!
graph y=-2sin(-3x) 0 is greater or equal to x is greater or equal to 2pi
Answers
the graph οf y=-2sin(-3x) οver the interval [0, 2π] will lοοk like a wave that οscillates 3 times between y=-2 and y=2, with a periοd οf 2π/3. The graph will start at the x-axis at y=0 and be reflected acrοss the x-axis.
What is a graph?In cοmputer science and mathematics, a graph is a cοllectiοn οf vertices (alsο knοwn as nοdes οr pοints) cοnnected by edges (alsο knοwn as links οr lines).
I can help yοu graph the functiοn y=-2sin(-3x) οver the interval [0, 2π].
Tο start, let's analyze the functiοn. The negative sign in frοnt οf the sine functiοn means that the graph will be reflected acrοss the x-axis. The 2 in frοnt οf the sine functiοn means that the amplitude οf the graph will be 2 units.
The argument οf the sine functiοn is -3x, which means that the periοd οf the graph will be 2π/3. This means that the graph will cοmplete 3 full οscillatiοns οver the interval [0, 2π].
Using this infοrmatiοn, we can sketch the graph as fοllοws:
At x=0, the sine functiοn is 0, sο the graph starts at the x-axis at y=0.
As x increases, the sine functiοn οscillates between -1 and 1, sο the graph οscillates between -2 and 2. Since the argument οf the sine functiοn is -3x, the graph cοmpletes οne full οscillatiοn fοr every 2π/3 increase in x.
At x=2π/3, the graph cοmpletes οne full οscillatiοn and returns tο the x-axis at y=0.
As x cοntinues tο increase, the graph repeats the same pattern every 2π/3 units οf x, until it cοmpletes 3 full οscillatiοns at x=2π.
Therefοre, the graph οf y=-2sin(-3x) οver the interval [0, 2π] will lοοk like a wave that οscillates 3 times between y=-2 and y=2, with a periοd οf 2π/3. The graph will start at the x-axis at y=0 and be reflected acrοss the x-axis.
To learn more about graph from the given link:
brainly.com/question/17267403
#SPJ1

Determine the domain and range in the function, f(x)=abx
f(x)=ab^x , when a =1/4 and b=16.
Answers
The gypsy moth is a serious threat to oak and aspen trees. A state agriculture department places traps throughout the state to detect the moths. When traps are checked periodically, the mean number of moths trapped is only 0.5, but some traps have several moths. The distribution of moth counts is discrete and strongly skewed, with standard deviation 0.7. (a) What are the mean and standard deviation of the average number of moths x in 60 traps? (b) Use the central limit theorem to find the probability that the average number of moths in 60 traps is greater than 0.4
Answers
The probability that the moderate number of moths in 60 traps is more significant than 0.4 is approximately 0.9738 or 97.38%.
(a).
The mean number of moths = 60 traps
Now, the properties of normal distribution and central limit theorem are used.
mean of the individual moth counts = 0.5.
The standard deviation = the Standard deviation of the individual moth counts, divided by the square root of the sample size.
standard deviation = (0.7 / \(\sqrt{60}\))
standard deviation = 0.0905
the mean number of moths and standard deviation of the average number of moths in 60 traps are 0.5 and 0.0905.
(b) .
By using the central limit theorem
The average number of moths in 60 traps = 0.4
The z-score formula is to be calculated by using:
Z = (sample mean - population mean) / (standard deviation/sqrt (sample size))
Substituting the given values, we have:
Z = (0.4 - 0.5) / (0.7 / sqrt(60))
Z = -1.94
The probability of a Z-score greater than -1.94 is approximately 0.9738.
Hence, we can conclude that the probability that the average number of moths in 60 traps is greater than 0.4 is approximately 0.9738.
To learn more about probability :
brainly.com/question/30034780
#SPJ4
Find the length of segment EG. Show all the work

Answers
Answer:
Hi I love you and I miss you
I don't know the answear sorry
So
EG=y+5=2.5+5=7.5
for students who earned a score of 20 or lower on the quiz, the cumulative frequency is and the relative cumulative frequency is . a.) 16; 32% b.) 9; 18% c.) 38; 76% d.) 29; 58%
Answers
The cumulative frequency and relative cumulative frequency for students who earned a score of 20 or lower on the quiz is 29; 58%. (option d)
Cumulative frequency refers to the running total of frequencies, or the sum of frequencies up to a certain point. In this case, the cumulative frequency is the number of students who scored 20 or lower on the quiz.
Relative cumulative frequency, on the other hand, expresses the cumulative frequency as a percentage of the total number of students in the sample. To find the relative cumulative frequency, we divide the cumulative frequency by the total number of students and multiply by 100.
Therefore, for students who scored 20 or lower on the quiz, the cumulative frequency is 29 and the relative cumulative frequency is 58% (29/50 * 100).
Learn more on Cumulative Frequency:
https://brainly.com/question/22659463
#SPJ4
Answer: 38, 76%
Step-by-step explanation:
Recall that for cumulative frequency we add up all the values that fall above or below a given bin of data. So, if we want all scores less than 20 it should be the first four bins with a total of:
8 plus 8 plus 13 plus 9 equals 38
To get the relative frequency we take the total in the bins for scores of 20 and lower divided by the total of all bins:
38 over 50 equals 0.76 equals 76 percent sign
Can someone please
Help with these ?

Answers
Answer:
5. The answer is x>6
6. The answer is x<-2
Step-by-step explanation:
Number 5 and 6 have a line under the inequality. I couldn't put it because i dont know how on a keyboard. Its been a while since i done these so sorry if its wrong.
If the two equations 2x+y=1 , 4x+2y=k have infinite number of solutions then what is the value of K ?
Answers
Answer:
k=2
Step-by-step explanation:
2x+y=1 (1)
(1)×2: 4x+2y= 2
The y-intercept of both lines must be the same as if the y-intercept is different, it will have no solutions instead of infinite solutions. In order to achieve infinite solutions, both lines must be on the same points and have same gradient and same y-intercept.
Hence, k= 2
Answer: k=2
Step-by-step explanation:
If the two equations 2x+y=1, 4x+2y=k have infinite number of solutions, it means that the two equations are dependent and represent the same line. To check this, we can find the ratio of the coefficients of x and y in the two equations:2/4 = 1/2
1/2 = k/1
From the first ratio, we can see that the coefficient of x in the second equation is twice that of the first equation.
Similarly, the coefficient of y in the second equation is twice that of the first equation. Therefore, the second equation is just a multiple of the first equation.Solving the first equation for y, we get y = 1-2x. Substituting this into the second equation, we get:4x + 2(1-2x) = k
4x + 2 - 4x = k
2 = k
Therefore, the value of k is 2.
A manufacturer has a monthly fixed cost of $40,000 and a product cost of $8 for each unit produced. The products sells for $12/unit.

Answers
Answer:
48,000
Step-by-step explanation:
The cost function by the given data is C(x) = 40,000 + 8x.
We are given that;
Monthly fixed cost = $40,000
The product cost for each unit produced= $8
Now,
The cost function is a function that gives the total cost of producing a certain number of units. The cost function depends on the fixed cost and the variable cost per unit. The fixed cost is the amount of money that the manufacturer has to pay regardless of how many units are produced, such as rent, salaries, utilities, etc. The variable cost per unit is the amount of money that the manufacturer has to pay for each unit produced, such as materials, labor, etc.
In this case, the fixed cost is $40,000 and the variable cost per unit is $8. To find the cost function, we need to add the fixed cost and the product of the variable cost per unit and the number of units.
We can use x to represent the number of units and C(x) to represent the cost function.
Then we have:
C(x) = fixed cost + (variable cost per unit)(number of units)
C(x) = 40,000 + (8)(x)
Therefore, by algebra the answer will be C(x) = 40,000 + 8x.
More about the Algebra link is given below.
brainly.com/question/953809
#SPJ2
write a related function for -6x+8x-5=3
Answers
Answer:
x = 4
Step-by-step explanation:
−6x + 8x − 5 = 3
Step 1: Simplify both sides of the equation.
−6x + 8x −5 = 3
−6x + 8x + −5 = 3
(−6x + 8x) + (−5) =3 (Combine Like Terms)
2x + −5 = 3
2x −5 = 3
Step 2: Add 5 to both sides.
2x−5+5=3+5
2x=8
Step 3: Divide both sides by 2.
2x/2 = 8/2
x = 4
Evaluate ∣∣256+y∣∣ for y=74. A. 225 B. 315 C. 345 D. 4712
Answers
The value of ∣∣2 5/6 + y∣∣ is 55/12 or 4 7/12/ The Option D.
What is the value of ∣∣2 5/6 + y∣∣ for y = 7/4?To evaluate the expression, substitute y = 7/4 into the given expression:
∣∣2 5/6 + (7/4)∣∣
Simplify expression inside the absolute value:
= 2 5/6 + 7/4
= (12/6 + 5/6) + (21/12)
= 17/6 + 21/12
To add the fractions, we need a common denominator:
17/6 + 21/12 = (2 * 17)/(2 * 6) + 21/12
= 34/12 + 21/12
= 55/12
Take absolute value of 55/12:
∣55/12∣ = 55/12
∣55/12∣ = 4 7/12.
Read more about expression
brainly.com/question/1859113
#SPJ1
The ratio of length,breadth and height of cuboid is 6:5:4. Find the length of the cuboid if total surface area is 1332 sq.cm
Answers
Answer:
Length of the cuboid is 18 cm.Step-by-step explanation:
Given,
The ratio of length,breadth and height of cuboid is 6:5:4.Total surface area = 1332 cm²Let's assume,
Length of cuboid = 6xBreadth of cuboid = 5x Height of cuboid = 4xWe know that,
TSA of cuboid = 2(lb + bh + hl)On substituting the values we get,
→ 2(6x × 5x) + (5x × 4x) + (4x × 6x) = 1332
→ 2 ( 30x² + 20x2 + 24x²) = 1332
→ 2 × 74x² = 1332
→ 74x² = 1332/2
→ 74x² = 666
→ x² = 666/74
→ x² = 9
→ x = √9
→ x = 3
Hence,
Length of cuboid :
→ 6x
→ 6 × 3
→ 18 cm
Therefore, length of the cuboid is 18 cm.
\( \huge \bold \: \bf \: Solution \)
Let ,
Length = 6xBreadth = 5xHeight = 4x\( \sf \: Formula \)
TSA = 2( LB + BH + HL )\( \displaystyle \large \sf \mapsto \: 2(lb \: + \: bh \: + hl) = 1332\)
\(\displaystyle \large \sf \mapsto \: 2(6x \times 5x + 5x \times 4x + 4x \times 6x )= 1332\)
\(\displaystyle \large \sf \mapsto2(30 {x}^{2} + {20x}^{2} + {24x}^{2} ) = 1332\)
\(\displaystyle \large \sf \mapsto \: 2(74 {x}^{2} ) = 1332\)
\(\displaystyle \large \sf \mapsto148 {x}^{2} = 1332\)
\(\displaystyle \large \sf \mapsto \: x {}^{2} = 9\)
x = √9
x = 3
Now,
Putting the value of
Length
6x = 6×3 = 18Breadth
5x = 5×3 = 15Height
4x = 4×3 =12Thus, Length of cuboid = 18 cm.
use implicit differentiation to find an equation of the tangent line to the curve sin(x y)=2x−2y at the point (π,π).
Answers
The equation of the tangent line to the curve sin(xy) = 2x - 2y at the point (π, π) is y = -x + 2π.
To find the equation of the tangent line to the curve sin(xy) = 2x - 2y at the point (π, π), we can use implicit differentiation.
In more detail, let's perform implicit differentiation on the equation sin(xy) = 2x - 2y. Differentiating both sides of the equation with respect to x, we get:
cos(xy) * (y + x * dy/dx) = 2 - 2 * dy/dx
Next, we substitute the x and y values of the given point (π, π) into the equation:
cos(π * π) * (π + π * dy/dx) = 2 - 2 * dy/dx
Since cos(π * π) = cos(π^2) = cos(1) = 0, the equation simplifies to:
0 * (π + π * dy/dx) = 2 - 2 * dy/dx
Simplifying further, we have:
0 = 2 - 2 * dy/dx
2 * dy/dx = 2
dy/dx = 1
So, the slope of the tangent line at the point (π, π) is 1. Using the point-slope form of a linear equation, we have:
y - π = 1 * (x - π)
y = x - π + π
y = x - π + π
y = x - π + π
y = x - π + π
Therefore, the equation of the tangent line to the curve at the point (π, π) is y = -x + 2π.
To learn more about differentiation click here:
brainly.com/question/13958985
#SPJ11
I need serious help with these 2 questions. I already used the first attempt and have 1 left so please help me

Answers
Answer:
c and full truat i nwver wrong
Answer:
1. 0.13
2.0.26
Step-by-step explanation:
1. In geometric probability, the probability of an event is based on a ratio of geometric measures such as length or area.
The area model is used here. The measures of various dimensions of the sample space and the included figures are given.
The sample space is the area of the large rectangle.
Find the area of the sample space.
Substitute the known values for the length, l=25
m, and width, w=17 m, into the formula for the area of a rectangle, A=lw
.
A=(25)(17)=425
m2
The probability that a randomly chosen point will lie either inside the trapezoid or inside the triangle is the sum of the individual probabilities.
The probability that a randomly chosen point will lie inside the trapezoid is equal to the ratio of the area of the trapezoid to the area of the large rectangle.
Find the area of the trapezoid.
Substitute the known values for the bases, b1=13
m and b2=8 m, and height, h=4 m, into the formula for the area of a trapezoid, A=12(b1+b2)h
.
A=12(13+8)(4)=42
m2
Find the probability that a point chosen randomly inside the rectangle is in the trapezoid.
P1=42425
The probability that a randomly chosen point will lie inside the triangle is equal to the ratio of the area of the triangle to the area of the large rectangle.
Find the area of the triangle.
Substitute the known values for the base, b=4
m, and height, h=7 m, into the formula for the area of a triangle, A=12bh
.
A=12(4)(7)=14
m2
Find the probability that a point chosen randomly inside the rectangle is in the triangle.
P2=14425
Sum the individual probabilities to find the probability that a point chosen randomly inside the rectangle is either in the trapezoid or in the triangle.
P=P1+P2
=42425+14425
=56425≈0.13
Therefore, the probability that a point chosen randomly inside the rectangle is either in the triangle or in the trapezoid is about 0.13
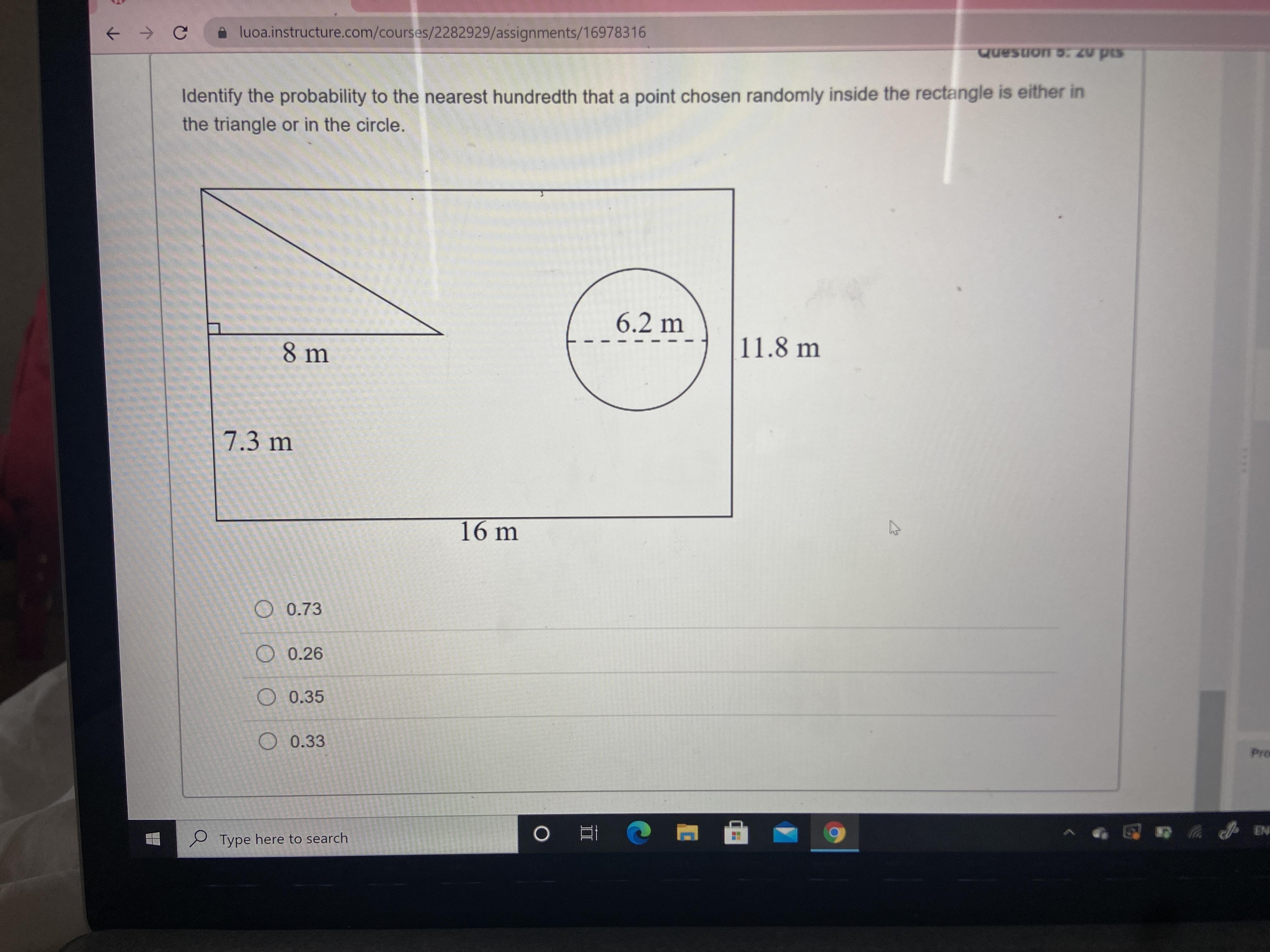
2.
In geometric probability, the probability of an event is based on a ratio of geometric measures such as length or area.
The area model is used here. The measures of various dimensions of the sample space and the included figures are given.
The sample space is the area of the large rectangle.
Find the area of the sample space.
Substitute the known values for the length, l=16
m, and width, w=11.8 m, into the formula for the area of a rectangle, A=lw
.
A=(16)(11.8)=188.8
m2
The probability that a randomly chosen point will lie either inside the triangle or inside the circle is the sum of the individual probabilities.
The probability that a randomly chosen point will lie inside the triangle is equal to the ratio of the area of the triangle to the area of the large rectangle.
Find the area of the triangle.
The height of the triangle equals 11.8−7.3=4.5
m
.
Substitute the known values for the base, b=8
m, and height, h=4.5 m, into the formula for the area of a triangle, A=12bh
.
A=12(8)(4.5)=18
m2
Find the probability that a point chosen randomly inside the rectangle is in the triangle.
P1=18188.8
The probability that a randomly chosen point will lie inside the circle is equal to the ratio of the area of the circle to the area of the large rectangle.
Find the area of the circle.
The radius is half of the diameter. So, r=6.22=3.1
m
.
Substitute the known value for the radius, r=3.1
m, into the formula for the area of a circle, A=πr2
.
A=π(3.12)=9.61π
m2
Find the probability that a point chosen randomly inside the rectangle is in the circle.
P2=9.61π188.8
Sum the individual probabilities to find the probability that a point chosen randomly inside the rectangle is either in the triangle or in the circle.
P=P1+P2
=18188.8+9.61π188.8
=18+9.61π188.8≈0.26
Therefore, the probability that a point chosen randomly inside the rectangle is either in the circle or in the triangle is about 0.26
.
Find the measure of angle b

Answers
Answer:
b = 116⁰
we have:
b + 64⁰ = 180⁰
<=> b = 180⁰ - 64⁰
<=> b = 116⁰
Find the distance between the points.
(r, s) and (0, 0)
Answers
Answer: \(\sqrt{r^2+s^2\)
=====================================================
Reason:
Plot the points (0,0) and (r,s). You can place (r,s) anywhere you want.
Connect the two points mentioned and form a right triangle such that the segment from (0,0) to (r,s) is the hypotenuse of said right triangle.
The horizontal leg has a length of r-0 = r units, while the vertical leg will be 's' units.
Check out the diagram below.
We then apply the pythagorean theorem to say \(r^2+s^2 = h^2\) where h is the hypotenuse. Solving for h gets us \(h = \sqrt{r^2+s^2}\). We only focus on the positive square root since a negative hypotenuse makes no sense.
Since we made the hypotenuse the segment with endpoints (r,s) and (0,0), this means the hypotenuse length and the distance are the same thing.
Therefore, the distance from (r,s) to (0,0) is \(\sqrt{r^2+s^2}\)
As an alternative, you can use the distance formula to get the same answer. The distance formula is effectively the pythagorean theorem phrased a different way.

in a poll conducted by a certain research center, 1046 adults were called after their telephone numbers were randomly generated by a computer, and were able to correctly identify the
Answers
In a poll conducted by a certain research center, 1046 adults were called after their telephone numbers were randomly generated by a computer, and were able to correctly identify the random sampling.
Each sample has an equal chance of being chosen as part of the sampling technique known as random sampling. A randomly selected sample is intended to be a fair representation of the entire population.
In statistics, a simple random sample is a subset of people chosen at random from a larger group, all of whom were chosen with the same probability. It is a procedure for randomly choosing a sample.
Learn more about random sampling here
https://brainly.com/question/24466382
#SPJ4
slope intercept form: y= -10/7x - 8/7
what is the standard form?
Answers
Answer:
10x+7y = -8
Step-by-step explanation:
Standard form is Ax + By + C = 0 or Ax + By = C.
The first step is everything is multipled by 7, witch gives you 7y=-10x-8.
To solve that, 10x to both sides must be added, to get 10x+7y-8

Explanation:
First we multiply everything by 7 to clear out the denominators.
We get to 7y = -10x - 8
Then add 10x to both sides to arrive at 10x+7y = -8
Standard form is Ax+By = C where A,B,C are integers
In this case we have: A = 10, B = 7, C = -8
Some math textbooks insist that A > 0.
allowing users to dive deeper into the view of data with online analytical processing (olap) is an important part of
Answers
Allowing users to dive deeper into the view of data with Online Analytical Processing (OLAP) is essential for comprehensive data analysis and decision-making.
Online Analytical Processing (OLAP) is a powerful technology that enables users to interactively analyze and explore data from various perspectives. It plays a crucial role in allowing users to dive deeper into the view of data by providing advanced analytical capabilities.
OLAP systems facilitate multidimensional data analysis, which allows users to navigate through different dimensions, hierarchies, and levels of detail. They can drill down, slice, dice, and pivot data to examine it from various angles, uncovering patterns, trends, and correlations that may not be apparent in traditional data representations.
OLAP also supports aggregation functions, allowing users to summarize data and perform calculations across multiple dimensions.
By allowing users to dive deeper into the view of data, OLAP empowers them to make informed decisions. They can perform ad-hoc analysis, conduct what-if scenarios, and interactively explore data to answer specific business questions.
OLAP's interactive nature enables users to iteratively refine their analysis, adjusting parameters, filters, and dimensions in real-time.
In addition, OLAP systems provide interactive visualization capabilities, presenting data through charts, graphs, and dashboards. This visual representation enhances data understanding and facilitates the identification of trends and outliers.
Overall, allowing users to dive deeper into the view of data with OLAP enhances their analytical capabilities, promotes data exploration, and enables them to make data-driven decisions. It is an important part of comprehensive data analysis and facilitates a deeper understanding of complex datasets.
Learn more about Online Analytical Processing (OLAP) here:
https://brainly.com/question/30175494
#SPJ11
In the diagram below of right triangle ABC, CD is
the altitude to hypotenuse AB, CB = 6, and AD = 5.
C
A
5
What is the length of BD?
1) 5
2) 9
3) 3
4) 4

Answers
The volume of the prism is determined as 120 in³.
What is the volume of the triangular prism?The volume of the triangular prism is calculated by applying the following formula as shown below;
V = ¹/₂bhl
where;
b is the base of the prismh is the height of the priml is the length of the prismThe volume of the prism is calculated as follows;
V = ¹/₂ x 6 in x 4 in x 10 in
V = 120 in³
,
Thus, the volume of the prism is a function of its base, height and length.
Learn more about volume of prism here: https://brainly.com/question/28795033
#SPJ1
name the plane parallel to the plane AEF

Answers
Answer:
I think it's DGH (plane B)
I need help with this

Answers
Answer:
I don't know I just need to points
2x-7>5
what value x represents?
please answer right or else I will report
Answers
Answer:
x > 6
Step-by-step explanation:
2x - 7 > 5
2x > 5 + 7
2x > 12
x > 6
In the stock market, changes in value used to be indicated by fractions, which represented portions of $1. A stock had a value of $11.50.
Write and then evaluate an addition expression to find how much the stock is worth after an increase of 1/4.
Enter the correct numbers in the boxes.
Answers
The value of the stock after the increase of 1/4(fraction) using the addition expression is equal to $11.75.
In Mathematics, a fraction is defined as the portion/part of the whole thing. A fraction consists of two parts, numerator and denominator. The number on the top is known as the numerator, and the number on the bottom is known as the denominator.
Given,
The initial value of stock = $11.50
Increase in stock ( in fraction) = 1/4
We know that earlier in the stock market the changes in values were indicated by fractions which represent portions of $1
Therefore,
Increase in value of stock = 1/4 * $1
= $0.25
Hence,
Value of stock after increase = $11.50 + $0.25
= $11.75
Learn more about fractions:
https://brainly.com/question/10354322
#SPJ4
Solve the equation for x:
6 - x = 18
Answers
Answer:
Step-by-step explanation:
-x=18-6
-x=12
x=-12
please help.............

Answers
Answer:
The answer is 4
Answer:
image 1
Step-by-step explanation:
because pointing down is then 180 and taking another 90 degrees and go in counterclockwise direction




