which expression is equivalent to (7x^3)^2 (x^8)
Answers
Answer:
49x^14
Step-by-step explanation:
Related Questions
I need help with 6,7,8 please

Answers
Answer:
6) 40°
7) 65°
8) 65°
Step-by-step explanation:
6) Total angle in a triangle is 180
180-70-70 = 40
7) y + 55 + 60 = 180
y = 65
8) 50 + n + n = 180
50 + 2n = 180
2n = 180 - 50
2n = 130
n = 130/2 = 65
find the area of the rhombus

Answers
Answer:
your answer will be option 2
120 units
Step-by-step explanation:
hope this helps have a nice day/ night !! ^_^
SLook at point in the coordinate grid.If a line contains both points and the origin, which point would the line also contain? *(2 points)DS(12,8)(14,7)(15,9)(20, 12)5tvAle--AR

Answers
the point which will fall in the line is (14, 7)
Explanation:
The coordinates o f S = (2, 1)
When we draw a line from the origin (0, 0) touching the point S, we will see the next point will be (4, 2). Followed by (6, 3).
So when we look at the trend, we see that the x axis is the double of the y axis:
(2y, y) = (x, y)
(2,1 ) , (4, 2), (6, 3)
From the above, we can say the point which will fall in the line will follow that trend:
When we check the options, the only point with that trend is (14, 7).
This because (2(7), 7) = (2y, y)
Hence, the point which will fall in the line is (14, 7)
i need someones help

Answers
Answer:
y = -1/3x - 2
Step-by-step explanation:
We can use the points (-1, -1) and (5, -3) to solve.
Slope formula is y2-y1/x2-x1
-3-(-1)/5-(-1)
-2/6
-1/3
Find the y intercept.
y = -1/3x + b
-1 = -1/3(-1) + b
-1 = 1 + b
-2 = b
y = -1/3x - 2
Best of Luck!
Louis and Michael met up for lunch. When they were done,
Louis traveled 4 blocks east and Michael traveled 1 blocks west. How many blocks away from Louis was Michael?
Answers
Answer:
five blocks away
Step-by-step explanation:
because 4 +1 =5
please if it is wrong let me know so I can correct
Explanation:
considering East and West are opposite from each other, all that is left to do, is add 4 and 1, which is 5
therefore, your answer is 5 blocks away
Chandler's house is due west of Springtown and due south of Livingston. Springtown is 6 miles from Chandler's house and 10 miles from Livingston. How far is Livingston from Chandler's house, measured in a straight line
Answers
Livingston is approximately 8.2 miles away from Chandler's house, measured in a straight line.
To find the distance between Livingston and Chandler's house, we can use the Pythagorean theorem because we have a right triangle formed by Springtown, Chandler's house, and Livingston.
Let's assign variables to the distances:
Let x be the distance from Livingston to Chandler's house (in miles).
Let y be the distance from Springtown to Chandler's house (in miles).
Given information:
Springtown is 6 miles away from Chandler's house (y = 6).
Livingston is 10 miles away from Springtown.
Using the Pythagorean theorem:
According to the theorem, the square of the hypotenuse (the distance between Livingston and Chandler's house) is equal to the sum of the squares of the other two sides.
Applying the theorem, we have:
x² = y² + (10)²
x² = 6² + 10²
x² = 36 + 100
x² = 136
Taking the square root of both sides:
x = √136
x ≈ 11.66
Therefore, Livingston is approximately 8.2 miles away from Chandler's house, measured in a straight line.
To learn more about straight line here:
brainly.com/question/31693341#
#SPJ11
what is integral of 1/square root of (a^2 - x^2)
Answers
For the given problem, the integral of \(\frac{1}{\sqrt{a^2-x^2}}\) is \($\sin^{-1}\frac{x}{a} + C$.\)
What is an 'integral' in mathematics?A mathematical notion that depicts the area under a curve or the accumulation of a quantity over an interval is known as an integral. Integrals are used in calculus to calculate the total amount of a quantity given its rate of change.
The process of locating an integral is known as integration. Finding an antiderivative (also known as an indefinite integral) of a function, which is a function whose derivative is the original function, is what integration is all about. The antiderivative of a function is not unique since it might differ by an integration constant.
For given problem,
\($\int \frac{1}{\sqrt{a^2-x^2}} dx$\)
Let \($x = a \sin\theta$\) , then \($dx = a \cos\theta d\theta$\)
\($= \int \frac{1}{\sqrt{a^2-a^2\sin^2\theta}} a\cos\theta d\theta$\)
\($= \int \frac{1}{\sqrt{a^2\cos^2\theta}} a\cos\theta d\theta$\)
\($= \int d\theta$\)
\($= \theta + C$\)
Substituting back for\($x = a\sin\theta$:\)
\($= \sin^{-1}\frac{x}{a} + C$\)
Therefore, the integral of \(\frac{1}{\sqrt{a^2-x^2}}\) is \($\sin^{-1}\frac{x}{a} + C$.\)
Learn more about intergal here:
https://brainly.com/question/31109342
#SPJ1
Find the value of x 10,26
Answers
The value of x for the given equation is 16.
What is the value of x?
To find the value of x in the equation x + 10 = 26, we need to isolate x on one side of the equation by performing the same operation to both sides of the equation.
We can start by subtracting 10 from both sides of the equation:
x + 10 - 10 = 26 - 10
Simplifying the left-hand side gives:
x = 16
Therefore, the value of x is 16, as this is the solution that satisfies the equation x + 10 = 26.
Learn more about linear equation here: https://brainly.com/question/2030026
#SPJ1
The complete question is below:
Find the value of x: for x +10 = 26
This season, the probability that the Yankees will win a game is 0. 61 and the probability that the Yankees will score 5 or more runs in a game is 0. 48. The probability that the Yankees lose and score fewer than 5 runs is 0. 32. What is the probability that the Yankees would score fewer than 5 runs when they lose the game? Round your answer to the nearest thousandth
Answers
Answer:
0.238
Step-by-step explanation:

A white blood cell has a diameter of approximately 12 micrometers, or 0.012 um. A model represents its diameter as 24 m. What is the ratio of model size to actual size? A. 200:1 B. 1:200 C. 2,000:1D. 1:2,000

Answers
It is given that,
The diameter of a white blood cell is 12 micrometers
The diameter of the white blood cells according to a model is 24 micrometers.
We need to find the ratio of model size to actual size. It can be done as follows :
\(R\text{ = }\frac{\text{ model size}}{\text{actual size}}\text{ = }\frac{24}{12}\text{ = }\frac{2,000}{1}\)So, the correct answer is C.
x+3.8>-10.02 what is the solution set
Answers
Answer:
x > -13.82
Step-by-step explanation:
i hope this helps :)
Answer:
{x | x ∈ R, x > -13.82}
Step-by-step explanation:
find the particular solution y=f(x) to the differential equation
Answers
To find the particular solution, we need additional information such as the initial condition \(y(x_0) = y_0\), where \(x_0\) and \(y_0\) are known values.
To find the particular solution to a differential equation, we need to know the specific form of the differential equation. Without this information, it is not possible to determine the particular solution.
A differential equation is an equation that relates a function and its derivatives. The form of the differential equation determines the method used to solve it and find the particular solution.
For example, a simple linear first-order ordinary differential equation has the form:
\(\frac{dy}{dx} = f(x)\).
To find the particular solution, we need additional information such as the initial condition \(y(x_0) = y_0\), where \(x_0\) and \(y_0\) are known values.
The method of solution depends on the specific type of differential equation, which can include linear equations, separable equations, exact equations, etc. Each type of equation requires different techniques to find the particular solution.If you provide the specific form of the equation you want to solve or any additional information or context, I can guide you through the process of finding the particular solution. Otherwise, without the differential equation, it is not possible to determine the particular solution.
Learn more about Equation here,https://brainly.com/question/29174899
#SPJ11
we assume that with a linear relationship between two variables, for any fixed value of x, the observed ________ follows a normal distribution.
Answers
We assume that with a linear relationship between two variables, for any fixed value of x, the observed residuals follows a normal distribution.
This assumption is based on the Central Limit Theorem, which states that when the sample size is large enough, the distribution of sample means will be approximately normal, regardless of the shape of the underlying population distribution.
In the case of a linear relationship between two variables, we can assume that the residuals (the difference between the observed y values and the predicted values based on the linear regression model) follow a normal distribution with mean 0 and constant variance. This assumption is important because it allows us to use statistical methods that rely on normality, such as hypothesis testing and confidence intervals.
Learn more about Normal distribution:
https://brainly.com/question/1846009
#SPJ11
Solve x2 – 5x – 24 = 0 by completing the square.Question 13 options:A) x = 6 and x = –4B) x = 3 and x = –8C) x = –3 and x = 8D) x = –6 and x = –4
Answers
Given:
\(x^2-5x-24=0\)First, let us keep the x terms on the left side and move the constant to the right side of the equation through adding 24 on both sides.
\(x^2-5x-24+24=0+24\)\(x^2-5x=24\)Next, we will take the half of the x term, 5x, and square it.
\((\frac{5}{2})^2=\frac{25}{4}\)And then, we will add this to both sides of the equation.
\(x^2-5x+\frac{25}{4}=24+\frac{25}{4}\)Then, we will rewrite the left side of the equation as a perfect square
\((x-\frac{5}{2})^2=\frac{121}{4}\)Take the square root of both sides
\(\sqrt[]{(x-\frac{5}{2})^2}=\sqrt[]{\frac{121}{4}}\)\(x-\frac{5}{2}=\pm\frac{11}{2}\)Solve for x (1)
\(x=\frac{5}{2}+\frac{11}{2}\)\(x=\frac{16}{2}\)\(x=8\)Solve for x (2)
\(x=\frac{5}{2}-\frac{11}{2}\)\(x=\frac{-6}{2}\)\(x=-3\)Now, we know that the values of x are -3 and 8, therefore, the answer would be C. x=-3 and x=8.
consider running golden section search on a function that is unimodal. if the method starts with an initial bracket of , what is the length of the bracket after 1 iteration?
Answers
The length of the bracket after 1 iteration is 100%.
Let f(x) = x³-15x² + 50x
a = 0, b=10.
Let the golden ratio be
GR=√5-1 / 2=0.618
Now, d = GR (b-a)
= 0.618 (10-0) = 6·18
\(x_{1}\)= a+d = 0 + 6·18 = 6.18
\(x_{2}\) = b-d = 10- 6·18 = 3.82
f(\(x_{1}\)) = (6·18)³ - 15 (6·18)² + 50(6·18) = -27.887
f(\(x_{2}\)) = (3.82)³-15(3.82)²+50(3.82)=27.857
so, f(\(x_{2}\)) > f(\(x_{1}\)) new interval is [a,x,]
i.e., maximum lies in [0, 6·18]
so, Xmax = \(x_{2}\)= 382
Uncertainty in measurement will be,
∈= \(\frac{1-GR) (b-a)}{Xopt}\) =\(\frac{((1-0.618) X (10-0)}{382}\) × 100%
∈ = 100%
In arithmetic, quantities are within the golden ratio if their ratio is the same as the ratio in their sum to the larger of the 2 portions. Expressed algebraically, for quantities a and b with \(a > b > 0\), \(\frac{(a+b)}{a}\) = \(\frac{a}{b}\)= φ
The golden ratio turned into known as the acute and suggest ratio by way of Euclid, and the divine proportion using Luca Pacioli, and also is going through numerous other names. The golden ratio seems in some patterns in nature, such as the spiral association of leaves and different elements of plants.
A few twentieth-century artists and architects, together with Le Corbusier and Salvador Dalí, have proportioned their works to approximate the golden ratio, believing them to be aesthetically appealing. these uses often appear in the form of a golden rectangle.
To learn more about the Golden Ratio visit here:
brainly.com/question/12450159
#SPJ4

Help me please!!!!!!!

Answers
Answer:
E = 100M/L
Step-by-step explanation:
we could cross-multiply to get:
E·L = 100M
now divide each side by L to get:
E = 100M/L
A pitching machine is programmed to pitch baseballs horizontally at a speed of 83 mph. The machine is mounted on a truck and aimed forward. As the truck drives toward you at a speed of 65 mph, the machine shoots a ball toward you. For each of the object pairings listed below, determine the correct relative speed. The speed of the pitching machine relative to the truck The speed of the pitched ball relative to the truck The speed of the pitching machine relative to you The speed of the to you 148 mph pitched ball relative zero 83 mph 65 mph 18 mph 170 mph 101 mph
Answers
The correct relative speeds are as follows The speed of the pitching machine relative to the truck: 83 mph2. The speed of the pitched ball relative to the truck: 0 mph3. The speed of the pitching machine relative to you: 18 mph4. The speed of the pitched ball relative to you: 101 mph.
When a pitching machine is programmed to pitch baseballs horizontally at a speed of 83 mph and the machine is mounted on a truck and aimed forward, the speed of the pitching machine relative to the truck is 83 mph.As the truck drives towards you at a speed of 65 mph and the machine shoots a ball towards you, the speed of the pitched ball relative to the truck is 0 mph. This is because both the truck and the ball are moving at the same speed in the same direction.Now, in order to determine the speed of the pitching machine relative to you, you need to consider the motion of both the truck and the ball.
Since the pitching machine is mounted on the truck and the ball is pitched horizontally, the ball moves in the same direction as the truck and has a horizontal velocity of 83 mph. Therefore, the relative speed of the pitching machine with respect to you is the difference between the speed of the truck and the horizontal velocity of the ball. This is given by:Relative speed of pitching
machine = 83 mph - 65
mph= 18 mph
Finally, the speed of the pitched ball relative to you can be determined by adding the speed of the truck to the horizontal velocity of the ball. This is given by:Relative speed of
ball = 83 mph + 65 mph= 148 mph
Therefore, the correct relative speeds are:1. The speed of the pitching machine relative to the truck: 83 mph2. The speed of the pitched ball relative to the truck: 0 mph3. The speed of the pitching machine relative to you: 18 mph4. The speed of the pitched ball relative to you: 101 mph
To know more about machine visit :
https://brainly.com/question/31828911
#SPJ11
Miles receives $6,000 from his parents. He wants to buy an used car that costs $12,500. If
he invests the money from his parents into an account that pays 7.5% interest compounded
continuously, how long will it take before he has a enough money to buy the car? Round your
answer to the nearest year.
Answers
Answer:
10 years
Step-by-step explanation:
principal = 6000
int = 7.5% annual compounding CONTINUOUSLY = everyday
so every day of the year he gets 7.5% / 365
so annual effective rate =7.7876%
so to get to 12500 it'll take t years
12500 = 6000* (1+ 7.7876% )^t
2.0833=1.077876^t
solve for t
approximately 10 years
Which expression is equivalent to
(4^5/4.4^1/4/4^1/2
Answers
Answer:
Which expression is equivalent to ((4^((5)/(4)).4^((1)/(4)))/(4^((1)/(2))))^((1)/(2))?
The ocean's surface is at 0. Which is farthest from the ocean’s surface?
A.
a fish swimming at -22 feet
B.
a kite flying at 48 feet
C.
a shipwreck at -52 feet
D.
a balloon at 19 feet
Answers
Answer:
C. a shipwreck at -52 feet
Step-by-step explanation:
It is asking which is farthest from the ocean's surface, so we must use absolute value.
\( | - 22| = 22 \\ |48 | = 48 \\ | - 52| = 52\\ |19| = 19\)
52 is greater than the others. therefore the farthest away.
Find the error & explain why it is wrong:
megan solved the following problem. what did she do wrong?
what is (f - g)(2)?
f(x) = 3x2 – 2x + 4
g(x) = x2 – 5x + 2
Answers
The value of (f-g)(2) is 16, provided that Megan has made no mistakes in the calculation.
Find the error in the given problem solved by Megan?The problem asks us to compute the value of (f - g)(2) where f(x) = 3x^2 - 2x + 4 and g(x) = x^2 - 5x + 2.
The notation (f - g)(2) means that we need to subtract g(x) from f(x) and then evaluate the result at x = 2. We can do this as follows:
(f - g)(x) = f(x) - g(x) = (3x^2 - 2x + 4) - (x^2 - 5x + 2) = 2x^2 + 3x + 2
Substituting x = 2, we get:
(f - g)(2) = 2(2)^2 + 3(2) + 2 = 16
Therefore, the value of (f - g)(2) is 16.
It's worth noting that the problem statement mentions "what did she do wrong?" without providing any context or information about what Megan did or didn't do. So, it's not possible to identify any error in Megan's solution based on the given information. However, based on the correct computation above, we can be sure that (f - g)(2) is indeed equal to 16.
In other words, it can be described as,
The error in Megan's solution is not clear from the given statement. However, it seems that she may have made an error while computing (f-g)(2).
To compute (f-g)(2), we need to subtract g(2) from f(2) as follows:
f(2) = 3(2)^2 - 2(2) + 4 = 12
g(2) = (2)^2 - 5(2) + 2 = -4
Therefore, (f-g)(2) = f(2) - g(2) = 12 - (-4) = 16. is the final conclusion.
Learn more about Solution
brainly.com/question/30198131
#SPJ11
Find the value of the variable and the measure of each angle.

Answers
Answer:
x = 14
(3x + 6)° = 48°
4x° = 56°
(2x + 6)° = 34°
Step-by-step explanation:
Given is the figure of a kite.
In a kite, diagonals intersects each other at right angles.
Therefore,
\((2x + 6) \degree + 4x \degree + 90 \degree = 180 \degree \\ \\ (2x + 6 + 4x) \degree = 180 \degree - 90 \degree \\ \\ (6x + 6) \degree = 90 \degree \\ \\ 6x + 6 = 90 \\ \\ 6x = 90 - 6 \\ \\ 6x = 84 \\ \\ x = \frac{84}{6} \\ \\ x = 14 \\ \\ (3x + 6) \degree = (3 \times 14 + 6) \degree = 48 \degree \\ \\ 4x\degree = 4 \times 14 \degree= 56 \degree \\ \\ (2x + 6) \degree = (2 \times 14 + 6) \degree = 34\degree\)
You used a student deck of 52 cards and selected a card at random find (c) 2 of heart
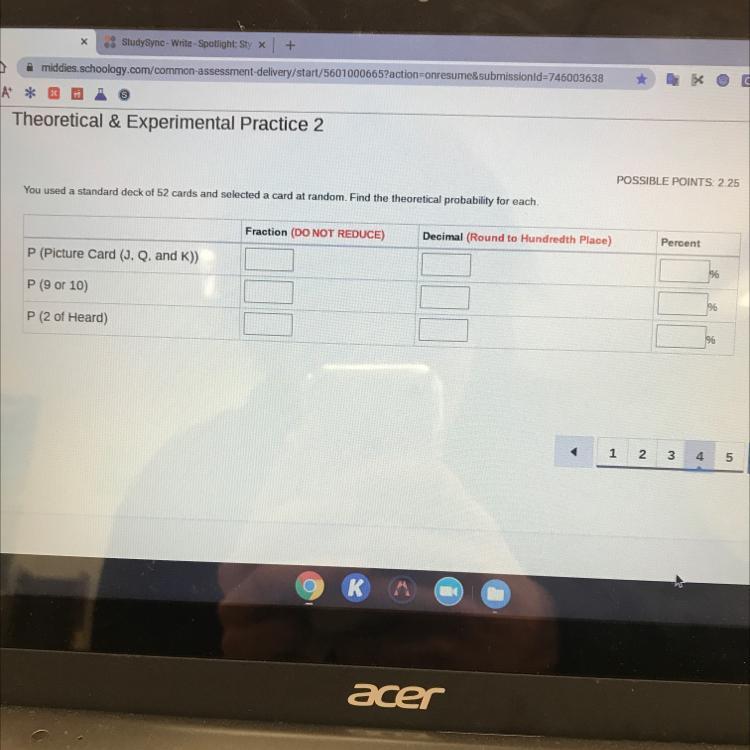
Answers
Definition
Theoretical Probability is the ratio of the number of favorable outcomes to the total possible outcomes of an event.
Expressing probability as a formula:
\(\text{probability = }\frac{Number\text{ of favorable outcomes}}{Total\text{ possible outcomes of an event}}\)Information about a standard deck of cards:
A standard deck of cards has four suits: hearts, clubs, spades, diamonds. Each suit has thirteen cards: ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, jack, queen, and king. Thus the entire deck has 52 cards total.
(a) Picture card (J, Q, and K)
In a standard deck, there are 4 Jacks, Queens, and Kings. Hence, the probability of J, Q, and K are:
\(\begin{gathered} \text{Number of picture cards = 4 }\times\text{ 3} \\ =\text{ 12} \end{gathered}\)Probability as a fraction:
\(=\text{ }\frac{12}{52}\)In decimal:
\(=\text{ }0.23\)Percent:
\(\begin{gathered} =\text{ 0.23 }\times\text{ 100} \\ =\text{ 23\%} \end{gathered}\)(b) 9 or 10
There are 4 cards labeled 9 and 10 each.
Probability as a fraction:
\(\begin{gathered} P(9or10)=\text{ P(9) + P(10)} \\ =\text{ }\frac{4}{52}\text{ + }\frac{4}{52} \\ =\text{ }\frac{8}{52} \end{gathered}\)In decimal:
\(=\text{ 0.15}\)In percent:
\(\begin{gathered} =\text{ 0.15 }\times\text{ 100} \\ =\text{ 15\%} \end{gathered}\)(c) 2 of heart
In a standard deck of cards, there are only one 2 of hearts.
Probability as a fraction:
\(=\text{ }\frac{1}{52}\)In decimal:
\(=\text{ 0.02}\)In percent:
\(\begin{gathered} =\text{ 0.02 }\times\text{ 100} \\ =\text{ 2\%} \end{gathered}\)I need help with this please
Answers
Recall that the interior angles of a triangle add up to 180 degrees, then:
\(m\angle A+m\angle B+m\angle C=180^{\circ}\text{.}\)Now, recall that a right angle measures 90 degrees.
Then we can set the following equation:
\(m\angle A+15^{\circ}+90^{\circ}=180^{\circ}.\)Adding like terms we get:
\(m\angle A+105^{\circ}=180^{\circ}.\)Subtracting 105 degrees from the above equation we get:
\(\begin{gathered} m\angle A+105^{\circ}-105^{\circ}=180^{\circ}-105^{\circ}, \\ m\angle A=75^{\circ}. \end{gathered}\)Answer:
\(75.0.\)What is the common ratio for the geometric sequence?
54,36, 24, 16...
Enter your answer in the box.
Answers
Step-by-step explanation:
First term (t1) = 54
second term (t2) = 36
Now
Common ratio (r)
\( = \frac{t2}{t1} \\ = \frac{36}{54} \\ = \frac{2}{3} \)
Hope it will help :)❤
x ^ 4 * y ^ 2 How many terms does this polynomial have?

Answers
Answer: 1 term
Step-by-step explanation:
Terms have to be separated by an Addition or Subtraction sign
If the sign is multiplication or division, then that part is only one term
explain why the following sequence cannot be generated using only the seq() and rep() functions in the same way as the sequences in (a). what makes this pattern different from the patterns in (a)? how can you generate this sequence? [1] 10 9 8 7 6 9 8 7 6 5 8 7 6 5 4 7 6 5 4 3 6 5 4 3 2 hint: since this sequence cannot be generated using only seq() and rep(), consider another operation in addition to seq() and rep() to combine simpler sequences into this more complicated pattern.
Answers
This will generate the desired sequence [1] 10 9 8 7 6 9 8 7 6 5 8 7 6 5 4 7 6 5 4 3 6 5 4 3 2. In this sequence, the numbers decrease from 10 to 1, then increase from 9 to 1, and so on.
The given sequence [1] 10 9 8 7 6 9 8 7 6 5 8 7 6 5 4 7 6 5 4 3 6 5 4 3 2 cannot be generated using only the seq() and rep() functions because it involves a more complex pattern than the sequences generated using seq() and rep() alone. In this sequence, the numbers decrease from 10 to 1, then increase from 9 to 1, and so on.
To generate this sequence, you can use the c() function in addition to seq() and rep(). The c() function is used to combine different elements or vectors into a single vector. Here is how you can generate this sequence:
1. Start by creating the decreasing sequence from 10 to 1 using seq() function:
seq(10, 1)
2. Next, create the increasing sequence from 9 to 1 using seq() function:
seq(9, 1)
3. Combine the above two sequences using the c() function:
c(seq(10, 1), seq(9, 1))
4. Repeat the combined sequence 6 times using rep() function:
rep(c(seq(10, 1), seq(9, 1)), times = 6)
Learn more about sequence
https://brainly.com/question/33469806
#SPJ11
b. Given Darcy's equation for the flow of fluid through a porous medium, derive a formula for calculating permeability. pressure gradient in the direction of the flow, (atm/cm). Hence calculate the permeability of a 20 cm long cylindrical core sample with the following laboratory linear flow test parameters: pressure differential =4.4 atm; fluid of viscosity 3.5cP; fluid velocity =0.032 cm/s.
Answers
The permeability of the cylindrical core sample is approximately 0.205 Darcy.
To derive the formula for calculating permeability, we start with Darcy's equation, which relates the flow of fluid through a porous medium to the pressure gradient in the direction of the flow. Darcy's equation is expressed as:
Q = (k * A * ∆P) / μL
Where:
Q is the flow rate of the fluid,
k is the permeability of the porous medium,
A is the cross-sectional area of flow,
∆P is the pressure differential,
μ is the fluid viscosity, and
L is the length of the flow path.
To calculate the permeability, we can use Darcy's equation: k = (Q * μ * L) / (A * ΔP), where k is the permeability, Q is the flow rate, μ is the fluid viscosity, L is the length of the sample, A is the cross-sectional area, and ΔP is the pressure differential.
The laboratory linear flow test parameters:
Q = fluid velocity = 0.032 cm/s,
μ = fluid viscosity = 3.5 cP,
L = length of the sample = 20 cm,
ΔP = pressure differential = 4.4 atm.
Let's assume the cross-sectional area A as 1 cm² for simplicity.
Plugging in these values into the equation, we have:
k = (0.032 * 3.5 * 20) / (1 * 4.4) ≈ 0.205 Darcy.
learn more about Darcy's equation here:
https://brainly.com/question/33288035
#SPJ11
Look at the equation
6x + 9 = 2x - 7
Which statement best explains how to isolate x to the left side of the equation?
A. Divide 6x by 2.
B. Add 6x and 2x.
C. Add 2 to each side.
D. Subtract 2x from each side.
Answers
switch sides to simplify
Michelle has $8 and wants to buy a combination of dog food to feed at least two dogs at the animal shelter. A serving of dry food costs $1, and a serving of wet food costs $3. This system of inequalities models the scenario: x + 3y ≤ 8 x + y ≥ 2 Part A: Describe the graph of the system of inequalities, including shading and the types of lines graphed. Provide a description of the solution set. (4 points) Part B: Is the point (8, 2) included in the solution area for the system? Justify your answer mathematically. (3 points) Part C: Choose a point in the solution set and interpret what it means in terms of the real-world context. (3 points)
Answers
Part A: The shaded region represents the feasible region where both inequalities are satisfied simultaneously. It is below the line x + 3y = 8 and above the line x + y = 2.
Part B: The point (8, 2) is not included in the solution area.
Part C: The point (3, 1) represents one feasible solution that meets the constraints of the problem.
Part A: The graph of the system of inequalities consists of two lines and a shaded region. The line x + 3y = 8 is a solid line because it includes the equality symbol, indicating that points on the line are included in the solution set. The line x + y = 2 is also a solid line. The shaded region represents the feasible region where both inequalities are satisfied simultaneously. It is below the line x + 3y = 8 and above the line x + y = 2.
Part B: To determine if the point (8, 2) is included in the solution area, we substitute the x and y values into the inequalities:
8 + 3(2) ≤ 8
8 + 6 ≤ 8
14 ≤ 8 (False)
Since the inequality is not satisfied, the point (8, 2) is not included in the solution area.
Part C: Let's choose a point in the solution set, such as (3, 1). This point satisfies both inequalities: x + 3y ≤ 8 and x + y ≥ 2. In the context of the real-world scenario, this means that Michelle can buy 3 servings of dry food (x = 3) and 1 serving of wet food (y = 1) with her $8 budget. This combination of dog food allows her to feed at least two dogs at the animal shelter while staying within her budget. The point (3, 1) represents one feasible solution that meets the constraints of the problem.
For more such questions on feasible region
https://brainly.com/question/29084868
#SPJ8