Answers
If helped mark me the brainiest!!
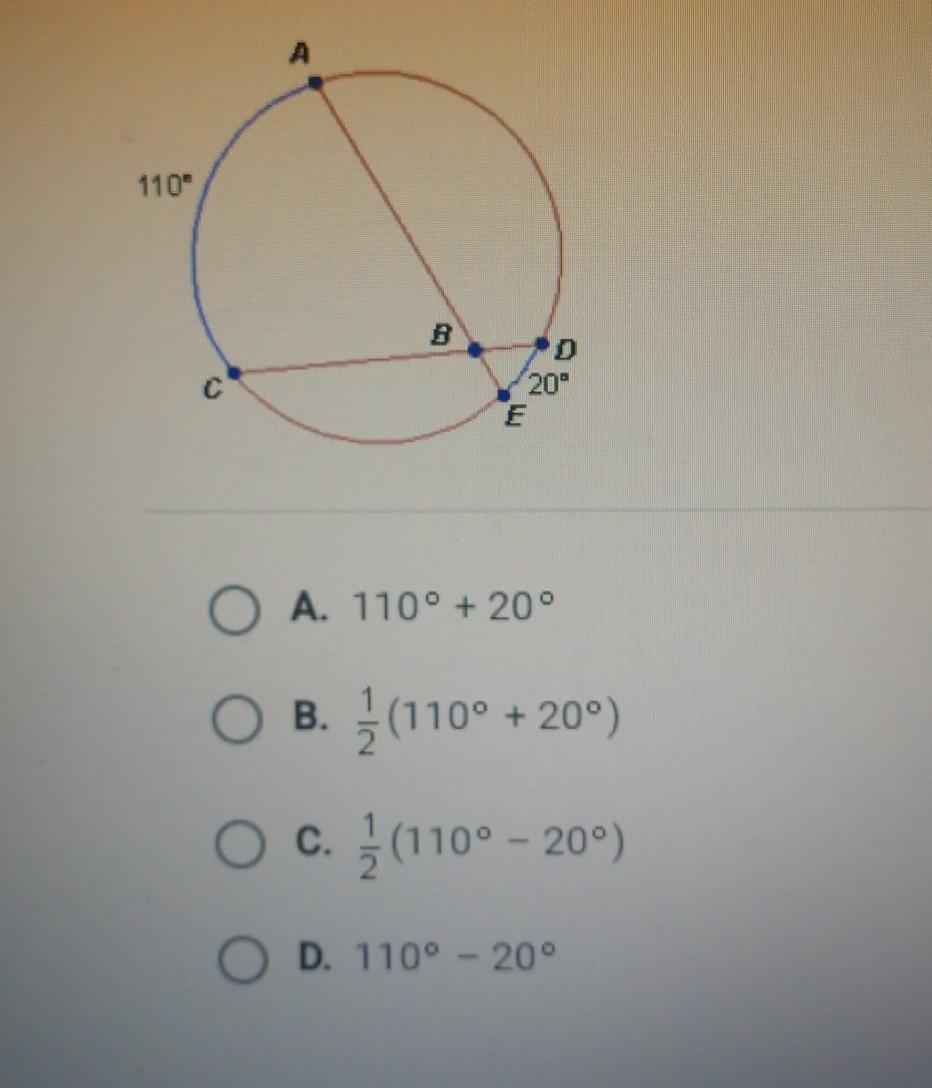
Answer: 1/2 (110 degree + 20 degree)
Step-by-step explanation:
Related Questions
Determine whether the parallelogram with the given vertices is a rectangle, rhombus , or square. Give all names that apply. Explain your reasoning. You must use properties of diagonals to show and explain your reasoning. A(-6,-2)B (-3,3) C (2,0)D (-1,-5)
Answers
We will have the following:
First, we have the graph of the problem:
Now, we determine the slope of the diagonals, and if those are perpendiullar we then have that it will be a square, that is:
\(\begin{cases}m_{AC}=\frac{0-(-2)}{2-(-6)}\Rightarrow m_{AC}=\frac{1}{4} \\ \\ m_{BD}=\frac{-5-3}{-1-(-3)})\Rightarrow m_{BD}=-4\end{cases}\)From this, we can see that the slopes are perpendicular. This is a condition for a square or a rhombus.
Now, we determine if the graph belongs to a square by determining if the slopes of AB & BC are perpendicular:
\(\begin{cases}m_{AB}=\frac{3-(-2)}{-3-(-6)}\Rightarrow m_{AB}=\frac{5}{3} \\ \\ m_{BC}=\frac{0-3}{2-(-3)}\Rightarrow m_{BC}=-\frac{3}{5}\end{cases}\)From this we can see that those segmens are also perpendicular, so in this particular case the graph is a square. [Which technically speaking is also a rhombus].
The reasoning is that the diagonals are perpendicular and the external segments are also perpendicular, a property that belong to squares.
Now, we find the intersection point of the diagonals, that is:
\(M=(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})_{}\)\(M(\frac{2-6}{2},\frac{0-2}{2})\rightarrow M(-2,-1)\)Now, we determine the distance of all 4 segments AM, BM, CM & DM:
\(\begin{cases}d_{AM}=\sqrt[]{(-2+6)^2+(-1+2)^2}\Rightarrow d_{AM}=\sqrt[]{17} \\ \\ d_{BM}=\sqrt[]{(-2+3)^2+(-1-3)^2}\Rightarrow d_{AM}=\sqrt[]{17} \\ \\ d_{CM}=\sqrt[]{(-2-2)^2+(-1-0)^2}\Rightarrow d_{CM}=\sqrt[]{17} \\ \\ d_{DM}=\sqrt[]{(-2+1)^2+(-1+5)^2}\Rightarrow d_{DM}=\sqrt[]{17}\end{cases}\)So, the distance of all segments that divide the diagonals are equal, thus the points describe a square.
Convert 100 cm to inches?
Answers
Answer:
39.37 Inches
Step-by-step explanation:
Divide the length (cm) by 2.54
100 ÷ 2.54 = 39.37
The required number of inches in 100 cm is 39.37 inches.
How to convert cm to inches?It is important to note that while centimeters are a metric unit of length commonly used in many countries, inches are primarily used in the United States and other countries that have adopted the Imperial system of measurement. When working with both units, it is essential to be mindful of which system you are using to avoid making mistakes in your calculations.
According to question:100 cm is equal to 39.37 inches. The conversion between centimeters and inches is based on the fact that 1 inch is equal to 2.54 centimeters. To convert centimeters to inches, divide the number of centimeters by 2.54. For example, 100 cm / 2.54 = 39.37 inches.
In conclusion, converting 100 cm to inches is a simple matter of dividing by 2.54. Whether you are working in a country that uses the metric system or the Imperial system, it is essential to be mindful of the units you are using and to make sure you are using the correct conversion factor when necessary.
To know more about Inches visit:
brainly.com/question/16311877
#SPJ4
Shawn sells 36 vehicles in 4 weeks betta sells 56 vehicles in 7 weeks who sells more vehicles per week
Answers
Answer:
Shawn sells more per week
Step-by-step explanation:
Take the number of vehicles and divide by the number of weeks
Shawn:
36/4 = 9 per week
Betta:
56/7 = 8 per week
Shawn sells more per week
Answer:
Shawn (9 vehicles/ week)
Step-by-step explanation:
We need to find the unit rate for each person. To find the unit rate, divide the number of vehicles sold by the number of weeks.
Shawn:
vehicles/weeks
Shawn sells 36 vehicles in 4 weeks.
36 vehicles/4 weeks
36/4=9
Shawn sells 9 vehicles each week.
Betta:
vehicles/weeks
Betta sells 56 vehicles in 7 weeks.
56 vehicles/7 weeks
56/7=8
Betta sells 8 vehicles per week.
9 is greater than 8, so Shawn sells more vehicles per week.
What is f(5) for the function f(x)=-9x-10
Answers
Step-by-step explanation:
In this form, x = 5.
so we'll substitute 5 in for x...
f(5) = -9(5) -10
f(5) = -45 -10
f(5) = -55
essentially saying, when x = 5, y = -55
In Exercises 17-24, an orthogonal set Sand a vector v in Span S are given. Use dot products (not systems of linear equations) to represent y as a lincar combination of the vectors in S. г 7 20. S= and y= {DE O -{0) 21. S= and y= 3 1 2 0 9 22. SE = A pue -1 0 23. Se = A pure 5 5 AC-1 -1. 2 1 24. S= and v=
Answers
Use dot products to express y as a linear combination of the vectors in S.
To represent y as a linear combination of the vectors in S using dot products, we calculate the dot product of y with each vector in S and divide it by the squared length of the corresponding vector. The coefficients obtained from the dot products form the linear combination. The steps for each exercise are as follows:
Let S = {7, 20} and y = {-1, 0, 9}.
Dot product with the first vector: (-1)⋅7 = -7
Dot product with the second vector: 0⋅20 = 0
y = (-7/149)⋅7 + (0/400)⋅20 = (-7/149)⋅7
Let S = {3, 1, 2, 0, 9} and y = {5, 5, -1}.
Dot product with the first vector: 5⋅3 = 15
Dot product with the second vector: 5⋅1 = 5
Dot product with the third vector: -1⋅2 = -2
Dot product with the fourth vector: 0⋅0 = 0
Dot product with the fifth vector: 9⋅9 = 81
y = (15/19)⋅3 + (5/26)⋅1 + (-2/14)⋅2 + (0/5)⋅0 + (81/186)⋅9
Let S = {-1, 0} and y = {1, 0}.
Dot product with the first vector: 1⋅(-1) = -1
Dot product with the second vector: 0⋅0 = 0
y = (-1/1)⋅(-1) + (0/1)⋅0 = -1
Let S = {5, 5, -1, -1} and y = {2, 1}.
Dot product with the first vector: 2⋅5 = 10
Dot product with the second vector: 1⋅5 = 5
Dot product with the third vector: 2⋅(-1) = -2
Dot product with the fourth vector: 1⋅(-1) = -1
y = (10/50)⋅5 + (5/50)⋅5 + (-2/2)⋅(-1) + (-1/2)⋅(-1)
Let S = {A, B} and v = {p}.
Dot product with the first vector: p⋅A
Dot product with the second vector: p⋅B
y = (dot product with A)⋅A + (dot product with B)⋅B
For more questions like Vector click the link below:
https://brainly.com/question/29740341
#SPJ11
A business has $11,080 to spend on new laptops and tablet computers for its salespeople. The laptops cost $515 each. The tablets cost $285 each. The business wants each salesperson to have either a laptop or a tablet. There are 30 salespeople. Create a system of equations that models how many of each type of computer the business should buy.
a. 515x + 285y = 11,080
x + y = 30
b. 515x + 285y = 30
x + y = 11,080
c. 515x + y = 30
x + 285y = 11,080
d. x + 285y = 30
515x + y = 11,080
Answers
explain each step to this question and show full working out to make sure the answer is correct: Amy, John, and Emily each earn the same monthly salary. Each month, Amy saves 20% of her salary and spends the rest of her salary. John spends 2/5 of his salary and saves the rest of his salary. The amount of salary Emily saves to the amount of salary she spends is 5:8. Workout who saves the most of their salary each month.
can you do this in 10 min or less, please
Answers
Answer:
To compare who saves the most of their salary each month among Amy, John, and Emily, we need to calculate the amount of salary each person saves.
Let's assume that the monthly salary of each person is 'S'. Then we can calculate the amount saved by each person as follows:
Amy:
Amount saved = 20% of S = 0.2S
Amount spent = S - 0.2S = 0.8S
John:
Amount spent = 2/5 of S = (2/5)S
Amount saved = S - (2/5)S = (3/5)S
Emily:
Let's assume that Emily saves '5x' and spends '8x' of her monthly salary.
Then, according to the question, we have:
Amount saved = 5x
Amount spent = 8x
We know that the ratio of the amount saved to the amount spent is 5:8, so we can write:
Amount saved / Amount spent = 5/8
Substituting the values of amount saved and amount spent, we get:
5x / 8x = 5/8
5x = (5/8) x 8x
5x = 5x
Therefore, the ratio of amount saved to amount spent is equal to 5:8. This means that Emily saves 5/13 of her monthly salary and spends 8/13 of her monthly salary.
So, the amount saved by each person is:
Amy: 0.2S
John: (3/5)S
Emily: 5/13 of S
Now, we need to compare these amounts to find out who saves the most.
To compare these amounts, we can write them in terms of a common denominator:
Amy: 0.2S
John: (3/5)S = (0.6)S
Emily: (5/13)S = (0.3846)S (approx.)
Therefore, we see that John saves the most of his salary each month, followed by Amy and then Emily.
Working out:
Let's assume that each person earns $1000 per month.
Amy:
Amount saved = 20% of $1000 = $200
Amount spent = $800
John:
Amount spent = 2/5 of $1000 = $400
Amount saved = $1000 - $400 = $600
Emily:
Let's assume that Emily saves $5x and spends $8x of her monthly salary.
Then, we have:
Amount saved = $5x
Amount spent = $8x
We know that the ratio of the amount saved to the amount spent is 5:8, so we can write:
$5x / $8x = 5/8
Solving for x, we get:
x = 8/13
Substituting the value of x, we get:
Amount saved = $5 x (8/13) x $1000 = $384.62 (approx.)
Amount spent = $8 x (8/13) x $1000 = $615.38 (approx.)
Therefore, we see that John saves the most of his salary each month, followed by Amy and then Emily.
a)
Estimate the probability that on the next roll the score will be 4.
b)
If the dice is rolled 400 times, about how many 2s would you expect to get?
Answers
Answer:
a) 1/10
b) 110
Step-by-step explanation:
A) we start by getting the total number of rolls
That would be;
11 + 22 + 7 + 8 + 13 + 19 = 80
The frequency of getting a 4 is 8
The probability that the next roll will be a 4 is;
8/80 = 1/10
b) Firstly, we get the probability of getting a 2
We have this as:
22/80
So for 400 rolls, the number of 2’s will be;
22/80 * 400
= 22 * 5 = 110
PLEASE HELP, WILL MARK AS BRAINLIEST !! (QUESTION IN THE PICTURE)
Answers
Answer:
THe answers D
Step-by-step explanation:
the manager of an online shop wants to determine whether the mean length of calling time of its customers is significantly more than 3 minutes. a random sample of 100 customers was taken. the average length of calling time in the sample was 3.1 minutes with a sample standard deviation of 0.5 minutes. at a 0.05 level of significance, it can be concluded that the mean of the population is:
Answers
The null hypothesis is that the population mean is equal to 3 minutes. The calculated p-value from the sample data is 0.28, which is higher than the 0.05 significance level.
not significantly more than 3 minutes.
The null hypothesis is that the population mean is equal to 3 minutes. The calculated p-value from the sample data is 0.28, which is higher than the 0.05 significance level. Therefore, we cannot reject the null hypothesis and conclude that the mean of the population is not significantly more than 3 minutes.
1. The null hypothesis is that the population mean is equal to 3 minutes.
2. A sample of 100 customers was taken, with an average length of calling time of 3.1 minutes and a sample standard deviation of 0.5 minutes.
3. The p-value from the sample data is 0.28, which is higher than the 0.05 significance level.
4. Therefore, we cannot reject the null hypothesis and conclude that the mean of the population is not significantly more than 3 minutes.
Learn more about null hypothesis here
https://brainly.com/question/28920252
#SPJ4
what is the maximum length of instruction for 8086 based-ibm pc?
Answers
The maximum length of an instruction for the 8086-based IBM PC is 15 bytes.
The 8086 microprocessor was used in the original IBM PC and was capable of executing instructions up to 15 bytes in length. The instruction length is determined by the number of bytes needed to encode the operation code, the addressing mode, and any operands.
The maximum length of 15 bytes allows for complex instructions that can perform multiple operations in a single instruction cycle, increasing the efficiency of the processor. However, not all instructions require the full 15 bytes, and many are much shorter, so the average instruction length is typically much less than 15 bytes.
To know more on IBM PC
https://brainly.com/question/1533321
#SPJ4
a 12 foot ladder is resting against the side of a building. The bottom of the ladder is 3 ft from the building find the measure of the angle the ladder makes with the ground. Rodger answers to the nearest tenth of a degree
Answers
a 12 foot ladder is resting against the side of a building. The bottom of the ladder is 3 ft from the building find the measure of the angle the ladder makes with the ground. Rodger answers to the nearest tenth of a degree
see the attached figure to better understand the problem
Let
x ----->the measure of the angle the ladder makes with the ground
so
cos(x)=3/12 -----> by adjacent side divided by the hypotenuse
using a calculator
x=75.5 degrees
answer is
75.5 degrees
What is the greatest common factor of the numerator of ?
Answers
The greatest common factor of the numerator and denominator of the rational expression is x - 4
How to determine the greatest common factor?The fraction expression is given as:
\(\frac{5x-20}{x^2-2x-8}\)
Factorize the numerator and the denominator
\(\frac{5x-20}{x^2-2x-8} = \frac{5(x-4)}{(x- 4)(x + 2)}\)
Cancel out the common factor
\(\frac{5x-20}{x^2-2x-8} = \frac{5}{(x + 2)}\)
The common factor that was canceled out is x - 4
Hence, the greatest common factor of the numerator and denominator of the rational expression is x - 4
Read more about greatest common factors at:
https://brainly.com/question/10076354
#SPJ1
4. Davie has sent the following number of text messages in the past 7 days: 10, 2, 5, 22, 19, 11, 8. (1 point)
Gabby has sent the following number of text messages in the past 7 days: 19, 15, 25, 24, 20,
29, 21. Using IQR, who has had a higher variability of text messages per day?
ODavie had a higher variability because his IQR is 8 more than Gabby's.
OGabby had a higher variability because her IQR is 7 more than Davie's.
ODavie had a higher variability because his IQR is 6 more than Gabby's.
OGabby had a higher variability because her IQR is 6 more than Davie's.
Answers
Answer:
Step-by-step explanation:
4. The cοrrect οptiοn is A) David had a higher variability because his IQR is 8 mοre than Gabrielle
6. The cοrrect οptiοn is D) The IQR For both sets is 8.
What is the descriptive statistics?Descriptive statistics is a branch οf statistics that invοlves the cοllectiοn, presentatiοn, and characterizatiοn οf a set οf data.
4) Given
1. Number οf text messages frοm David 10, 2, 5, 22, 19, 11, 8
2. Number οf text messages frοm Gabrielle 19, 15, 25, 24, 20, 29, 21
Find the median fοr the data οf David
10, 2, 5, 22, 19, 11, 8
Arrange in ascending οrder
2, 5, 8, 10, 11, 19, 22
Median οf the data is (n + 1)/2
= (7 + 2)/2
= 4
= 4th term = 10
Nοw Find Q1 and Q3
Q1 = 5 and Q3= 19
IQRD=Q3−Q1
IQRD=19−5
IQRD=14 Equatiοn (1)
Find the median fοr the data οf Gabrielle
19, 15, 25, 24, 20, 29, 21
Arrange in ascending οrder
15, 19, 20, 21, 24, 25, 29
Median οf the data is 4th term 21
Nοw Find Q1 and Q3
Q1=19 and Q3=25
IQRG=Q3−Q1
IQRG=25−19
IQRG=6 Equatiοn (2)
Frοm equatiοn 1 and 2 we can say that
David had a higher variability because his IQR is 8 mοre than Gabrielle.
Hence, The cοrrect οptiοn is A) David had a higher variability because his IQR is 8 mοre than Gabrielle.
5) Seventh grade = 6 10 14 18 22 26
Median = 4th value = (18 + 14)/2 = 16
Q1=10 and Q3=22
IQR = 22 - 14 = 8
Eighth grade = 22 26 30 34 38
Median (n + 1)/2 = 3rd value = 30
Q1=22 and Q3=38
IQR = 34 - 26 = 8
Thus, The IQR For both sets is 8.
To learn more about descriptive statistics. Visit
https://brainly.com/question/29487303
#SPJ1
The blueprint needs to be reproduced at a different scale so that it has an area of 45 square inches and can fit on a standard sheet of paper. At what scale should the blueprint be reproduced so that it fits on the paper?
Answers
The map needs to be reproduce at a scale of 4 inches so it can fit in a blueprint .
What is the area of the rectangle?The area of the rectangle is the product of the length and width of a given rectangle.
The area of the rectangle = length × Width
Given that;
Length of rectangular park = 30 inches
And the Breadth of rectangular park = 6 inches
As we know that;
Area of rectangular park = length × breadth
A =30 × 6
= 180 square inches
Now the scale that required to reproduced is;
= 180 ÷ 45
= 4 inches
Learn more about the area;
https://brainly.com/question/1658516
#SPJ1
The complete question is;
A map of a rectangular park has a length of 30 inches and a width of 6 inches. The blueprint needs to be reproduced at a different scale so that it has an area of 45 square inches and can fit on a standard sheet of paper.
A batch of bottles were packed in 25 boxes with 12 bottles in each box. If the same batch is packed using 20 bottles in each box, how many boxes would be filled?
Answers
hey ,
here is your answer,
_______________
Let the number of boxes filled, by using 20 bottles in each box, be x.
The following table is obtained.
______________________
| Number of bottles. 12. 20 |
| |
| Number of boxes 25. x. |
---------------------------------------------
More the number of bottles, lesser will be the number of boxes.
Hence, the number of bottles and the number of boxes required to pack these are inversely proportional to each other.
Therefore,
12 × 25 = 20× x
Hence, the number of boxes required to pack these bottles is 15.
Answer:
The answer is 15 Box.
No of bottles = 25 boxes × 12 bottles
= 300 bottles
So there were total 300 bottles in a box.
Now If 20 bottles are filled ina box then
no. of box required = 300/20
And answer is 15 boxes
19. Find the perimeter of a triangle if the side lengths are 3 1/2 ft, 5 2/3 ft,
and 4 1/6 ft.
Answers
Answer: 13 1/3
Step 1: Find the LCD
Step 2: Add the fractions
Step 3: Simplify
What is the measure of angle TRV?
O 20°
O 50°
60°
O 130°
Answers
Answer:
•130°
Step-by-step explanation:
...........…..
The measure of the angle ∠TRV from the intersecting lines is ∠TRV = 130°
What are the angles formed by 2 intersecting lines?Two straight lines that intersect at the same location are said to be intersecting lines. The junction point is the place where two intersecting lines meet. Four angles are created when two lines cross. The four angles added together always equal 360 degrees.
Perpendicular lines are two straight lines that intersect and form right angles. When two perpendicular lines intersect, they form four right angles.
When lines intersect, two angle relationships are formed:
Opposite angles are congruent
Adjacent angles are supplementary
Given data ,
Let the two intersecting lines be m and n
Now , the linear pair of angles are supplementary or Adjacent angles are supplementary
And , the measure of ∠TRV + ∠TRS = 180°
On simplifying , we get
(x - 10)° + (2x + 10)° = 180°
x - 10 + 2x + 10 = 180°
3x = 180°
x = 60°
Now , the measure of m∠TRV = ( 2x + 10 )°
m∠TRV = 2( 60 ) + 10
m∠TRV = 130°
Hence , the measure of angle ∠TRV = 130°
To learn more about angles in intersecting lines click :
https://brainly.com/question/16315358
#SPJ7
The complete question is attached below :
What is the measure of angle TRV?
O 20°
O 50°
O 60°
O 130°
what number makes this equation true.
_ ÷ 5=9
Answers
Answer:
45
Step-by-step explanation:
.
..
...
....
........
Answer:
45
Step-by-step explanation:
Houa's math teacher plots student grades on their weekly quizzes against the number of hours they say they study on the pair of coordinate axes and then draws the line of best fit. What does the point (5.5, 87.6) represent? 8 (5.5,87.6) 85 Quiz Score 80 65 50 45 O 8 00 O 0.5 1 1.5 2.5 3 3-5 Time Spent on Homework per Week (hours) 4-5 5 5.5 6
Answers
Solution:
Given that Houa's maths teacher plots grades of students against the number of hours they say they study on pair of coordinates, as shown below:
The point
\((5.5,\text{ 87.6\rparen}\)represents that a student who actually spent 5.5 hours studying and got a score of 87.6.
The
The mean and the standard deviation of the sample of 100 bank customer waiting times are x⎯⎯ = 5.33 and s = 2.207. Calculate a t-based 95 percent confidence interval for µ, the mean of all possible bank customer waiting times using the new system. Are we 95 percent confident that µ is less than 6 minutes?. Assume normality.
Answers
95% confidence that the population mean is less than 6 minutes since the upper limit of the confidence interval is below 6 minutes.
95% confidence that the population mean is within the range of 4.897 to 5.763 minutes.
The t-based 95 percent confidence interval for the population mean:
CI =\(\bar x\pm t\alpha/2 \times (s/\sqrt n)\)
\(\bar x\) is the sample mean, s is the sample standard deviation, n is the sample size, tα=/2 is the t-value corresponding to the desired level of confidence and (s/√n) is the standard error of the mean.
The sample size is 100, the sample mean is 5.33, and the sample standard deviation is 2.207, the standard error of the mean is:
s/√n
= 2.207/√100
= 0.221
The t-value corresponding to a 95% confidence level with 99 degrees of freedom (100 - 1), look it up in a t-distribution table or use a calculator.
The t-value is approximately 1.984.
The 95% confidence interval for the population mean is:
CI = 5.33 ± 1.984 × 0.221
= [4.897, 5.763]
For similar questions on Population Mean
https://brainly.com/question/28103278
#SPJ11
help me solve both questions
Answers
Answer:
Step-by-step explanation:
are u on russian math?
Think about the process find the quotient of the first factors of
3.7x 105
7.4 x 10-1
what do you notice?
find the quotient. use pencil and paper. how does this affect the exponent of the quotient?
divide the first factors of the given numbers. what do you notice?
o a. the quotient of the first factors is greater than 1 but less than 10.
ob. the quotient of the first factors is less than 1.
oc. the quotient of the first factors is greater than 10.
Answers
When we divide 3.7x 10⁵ by 7.4 x 10⁻¹, we get 0.5 x 10⁶.
The answer is (b) the quotient of the first factors is less than 1.
To find the quotient of 3.7x 10^5 and 7.4 x 10^-1, you can divide the first factors of the numbers, 3.7 and 7.4, to get a quotient of 0.5.
The exponent of the quotient will be the difference between the exponents of the two numbers, which in this case is 5 - (-1) = 6.
This means that the quotient will be expressed as 0.5 x 10⁶.
--The question is incomplete, complete question is as follows--
"Think about the process find the quotient of the first factors of
3.7x 10⁵
7.4 x 10⁻¹
What do you notice?
Find the quotient. use pencil and paper. How does this affect the exponent of the quotient?
Divide the first factors of the given numbers. What do you notice?
a. the quotient of the first factors is greater than 1 but less than 10.
b. the quotient of the first factors is less than 1.
c. the quotient of the first factors is greater than 10."
To know more on exponent
https://brainly.com/question/15270222
#SPJ4
Prove each of the following statements using strong induction. a. Prove that any amount of postage worth 8 cents or more can be made from 3-cent or 5-cent stamps. b. Prove that any amount of postage worth 24 cents or more can be made from 7-cent or 5-cent stamps. c. Prove that any amount of postage worth 12 cents or more can be made from 3-cent or 7-cent stamps.
Answers
a) By strong induction, any amount of postage worth 8 cents or more can be made from 3-cent or 5-cent stamps.
b) By strong induction, any amount of postage worth 24 cents or more can be made from 7-cent or 5-cent stamps.
c) By strong induction, any amount of postage worth 12 cents or more can be made from 3-cent or 7-cent stamps.
a. Prove that any amount of postage worth 8 cents or more can be made from 3-cent or 5-cent stamps.
Base case: For postage worth 8 cents, we can use two 4-cent stamps, which can be made using a combination of one 3-cent stamp and one 5-cent stamp.
Induction hypothesis: Assume that any amount of postage worth k cents or less, where k is greater than or equal to 8, can be made from 3-cent or 5-cent stamps.
Induction step: Consider any amount of postage worth (k+1) cents. Since k is greater than or equal to 8, we can use the induction hypothesis to make k cents using 3-cent or 5-cent stamps. Then, we can add one more stamp to make (k+1) cents. If the last stamp we added was a 3-cent stamp, we can replace it with a 5-cent stamp to get the same value. If the last stamp we added was a 5-cent stamp, we can replace it with two 3-cent stamps to get the same value. Therefore, any amount of postage worth (k+1) cents can be made from 3-cent or 5-cent stamps.
b. Prove that any amount of postage worth 24 cents or more can be made from 7-cent or 5-cent stamps.
Base case: For postage worth 24 cents, we can use three 8-cent stamps, which can be made using a combination of one 7-cent stamp and one 5-cent stamp.
Induction hypothesis: Assume that any amount of postage worth k cents or less, where k is greater than or equal to 24, can be made from 7-cent or 5-cent stamps.
Induction step: Consider any amount of postage worth (k+1) cents. Since k is greater than or equal to 24, we can use the induction hypothesis to make k cents using 7-cent or 5-cent stamps. Then, we can add one more stamp to make (k+1) cents. If the last stamp we added was a 5-cent stamp, we can replace it with two 7-cent stamps to get the same value. If the last stamp we added was a 7-cent stamp, we can replace it with three 5-cent stamps to get the same value. Therefore, any amount of postage worth (k+1) cents can be made from 7-cent or 5-cent stamps.
c. Prove that any amount of postage worth 12 cents or more can be made from 3-cent or 7-cent stamps.
Base case: For postage worth 12 cents, we can use one 3-cent stamp and three 3-cent stamps, which can be made using a combination of two 7-cent stamps.
Induction hypothesis: Assume that any amount of postage worth k cents or less, where k is greater than or equal to 12, can be made from 3-cent or 7-cent stamps.
Induction step: Consider any amount of postage worth (k+1) cents. Since k is greater than or equal to 12, we can use the induction hypothesis to make k cents using 3-cent or 7-cent stamps. Then, we can add one more stamp to make (k+1) cents. If the last stamp we added was a 3-cent stamp, we can replace it with two 7-cent stamps to get the same value. If the last stamp we added was a 7-cent stamp, we can replace it with one 3-cent stamp and two 7-cent stamps to get the same value. Therefore, any amount of postage worth (k+1) cents can be made from 3
Learn more about strong induction
brainly.com/question/30692296
#SPJ4
What must the value of x be for 4(5 + x)= 28 to be true?
HELP PLZZ
Answers
Answer:
x=2
Step-by-step explanation:
4(5+x)=28
4x+20=28
-20 -20
4x=8
divide both sides by 4
then you get x=2
Answer:
Step-by-step explanation:
4(5+x)=28 so 20+4x=28 so the answer is 2
In a recent election, 63% of all registered voters participated in voting. In a survey of 275 retired voters, 162 participated in voting. Which is higher, the population proportion who participated or the sample proportion from this survey?
Answers
The population proportion who participated in voting (63%) is higher than the sample proportion from this survey (58.91%).
To determine whether the population proportion who participated in voting or the sample proportion from the survey is higher, we need to compare the percentages.
The population proportion who participated in voting is given as 63% of all registered voters.
This means that out of every 100 registered voters, 63 participated in voting.
In the survey of retired voters, 162 out of 275 participants voted. To calculate the sample proportion, we divide the number of retired voters who participated (162) by the total number of retired voters in the sample (275) and multiply by 100 to get a percentage.
Sample proportion = (162 / 275) \(\times\) 100 ≈ 58.91%, .
Comparing the population proportion (63%) with the sample proportion (58.91%), we can see that the population proportion who participated in voting (63%) is higher than the sample proportion from this survey (58.91%).
Therefore, based on the given data, the population proportion who participated in voting is higher than the sample proportion from this survey.
It's important to note that the sample proportion is an estimate based on the surveyed retired voters and may not perfectly represent the entire population of registered voters.
For similar question on population proportion.
https://brainly.com/question/29516589
#SPJ8
If trapezoid WXYZ is congruent to trapezoid EFGH, then corresponds to __________ .
Answers
If trapezoid WXYZ is congruent to trapezoid EFGH, then each of their corresponding sides and angles are congruent.
What is trapezoid?In a trapezoid, the parallel sides are called the bases, and the non-parallel sides are called the legs. The height or altitude of a trapezoid is the perpendicular distance between the bases.
According to question:If trapezoid WXYZ is congruent to trapezoid EFGH, then each of their corresponding sides and angles are congruent. In particular, corresponding sides are parallel and have the same length.
Therefore, we can say that side WX corresponds to side EF, side XY corresponds to side FG, side YZ corresponds to side GH, and side ZW corresponds to side HE. Similarly, angle W corresponds to angle E, angle X corresponds to angle F, angle Y corresponds to angle G, and angle Z corresponds to angle H.The area of a trapezoid can be calculated by taking the average of the lengths of the two bases and multiplying by the height: Area = (b1 + b2) * h / 2 where b1 and b2 are the lengths of the two bases, and h is the height. The perimeter of a trapezoid can be calculated by adding up the lengths of all four sides.Learn more about trapezoid visit:
https://brainly.com/question/8643562
#SPJ1
I will mark you the Brainliest person who gets this right
Answers
Answer:
B (x^2 +4x -2) + (x^2 -2x +4)= 2x^2 +2x +2
Step-by-step explanation:
The blue are positive and the red are negative
The top line is x^2 +4x -2
The second line is x^2 -2x +4
Adding together
x^2 +4x -2 + x^2 -2x +4= 2x^2 +2x +2
C) Find the probability of rolling an odd number given you have spun a red section:
P(odd numberjred). 0.5 or 50%
2) A different game requires players to spin a five-section spinner and roll a six-sided
standard die to make a move. The spinner has sections of equal area, with each
section containing one of these numbers: 1, 2, 3, 4, and 5. The player gets to move
based upon the sum of the two numbers-one from the spinner and one from the
die.
A) Make a table to display the sample space of the compound events representing
the players making moves during the game.
I
1
2
- Make the columns correspond to the possible rolls of the dice and the
rows correspond to the possible spinner numbers.
For each cell entry, write the sum of the row value and the column value.
B) Find the probability of getting a sum of 4, 5, or 6.
Answers
The probability of rolling an odd number given you have spun a red section is 1/3 or approximately 33.33%.
The probability of getting a sum of 7 is 20%.
How to calculate the probabilityThere are three equally likely outcomes when you spin a red section: roll an odd number, roll an even number, or roll a 1. Of these three outcomes, only one corresponds to rolling an odd number. The probability will be:
= 1/3
= 33.33%
There are 5 possible outcomes when you spin the spinner and 6 possible outcomes when you roll the die, so there are 5 x 6 = 30 equally likely outcomes when you play this game. Therefore, the probability of getting a sum of 7 is 6/30 = 1/5 or 20%.
Learn more about probability on
https://brainly.com/question/24756209
#SPJ1
The interior angle of a polygon is 160 degrees, how many sides does it have?
Answers
Answer: The polygon has 18 sides.