Which equation represents the circle shown?
A. (x − 3)2 + (y − 3)2 = 4
B. (x − 3)2 + (y − 3)2 = 16
C. (x + 3)2 + (y + 3)2 = 4
D. (x + 3)2 + (y + 3)2 = 16
E. (x + 4)2 + (y + 4)2 = 3
Answers
B. (x-3)2+(y-3)2=16
Equation of circle is
(x-a)2+(y-b)2=r2
Related Questions
6th grade math i mark as brainliest

Answers
Answer:
A and D
Step-by-step explanation:
-14 is less than -8 because is further away from 0
State YOUR thoughts/reactions
WRITE AT LEAST 4 COMPLETE SENTENCES IN PARAGRAPH FORMAT.
When Saul died, David was crowned king. David united the tribes and continued the fight against the Philistines and other enemies. He captured Jerusalem and made it his capital, starting its transformation into one of history’s most important cities.
David’s son Solomon inherited a peaceful kingdom. He built a great stone temple in Jerusalem. Solomon’sTemple became the focus of religious life. Solomon used trade and taxes to fund other huge building projects. However, most of the tax burden fell on the northern tribes, who came to resent Solomon’s
Answers
Answer:
All you have to do is write how you feel about this it's simple :|
Step-by-step explanation:
Which statement describes why AABC and ADEF are congruent by SAS?

Answers
Answer:It is The first one.
Step-by-step explanation:
what is the solution?
x=3 and y=4
x=5 and y=4
x=4 and y=3
x=3 and y=2
Answers
Answer:
give me more instructions so i can actually help
Step-by-step explanation:
help with 6 please i need to graduate
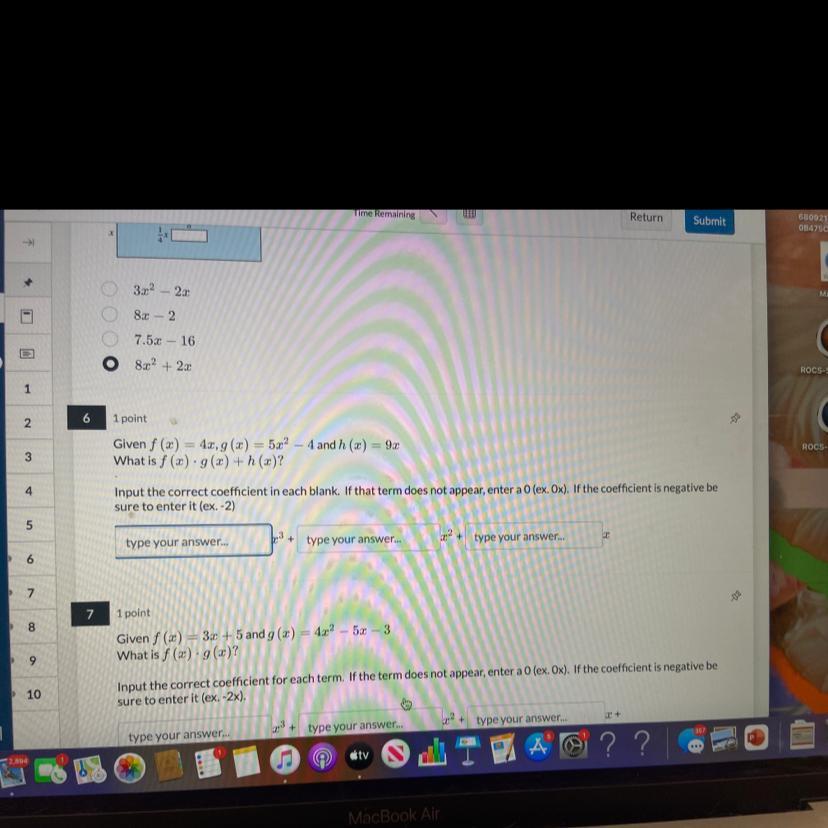
Answers
The expression with the correct coefficients in each block is given as follows:
20x³ + 0x² - 7x.
How to obtain the resultant function?The functions in the context of this problem are defined as follows:
f(x) = 4x.g(x) = 5x² - 4.h(x) = 9x.The operation is given as follows:
f(x)g(x) + h(x).
Hence, to obtain the resultant function, we apply the definitions into the operation and the simplify, applying the distributive property and combining the like terms, as follows:
4x(5x² - 4) + 9x = 20x³ - 16x + 9x = 20x³ - 7x.
As there is no x² term, the coefficient of zero multiplies the term x².
More can be learned about functions at https://brainly.com/question/31895757
#SPJ1
Solve the following quadratic inequality x^2+x-6>0
Answers
Answer:
x < -3 or x > 2
Step-by-step explanation:
x² + x - 6 > 0
Convert the inequality to an equation.
x² + x - 6 = 0
Factor using the AC method and get:
(x - 2) (x + 3) = 0
If any individual factor on the left side of the equation is equal to 0, the entire expression will be equal to 0.
x - 2 = 0
x = 2
x + 3 = 0
x = -3
So, the solution is x < -3 or x > 2
10.8.8 Check Your Understanding
Allison went on a business trip and stayed at a hotel for three nights. She paid a total of $782.07 for the room and to
park her car. Each night, the hotel charged d dollars and $17.20 for parking. Which equation represents the total
amount, in dollars, Allison paid for the three nights?
A) d+3(17.20) = 782.07
(B) 3d+17.20 = 782.07
C) 3(d-17.20) = 782.07
D) 3(d+17.20) = 782.07
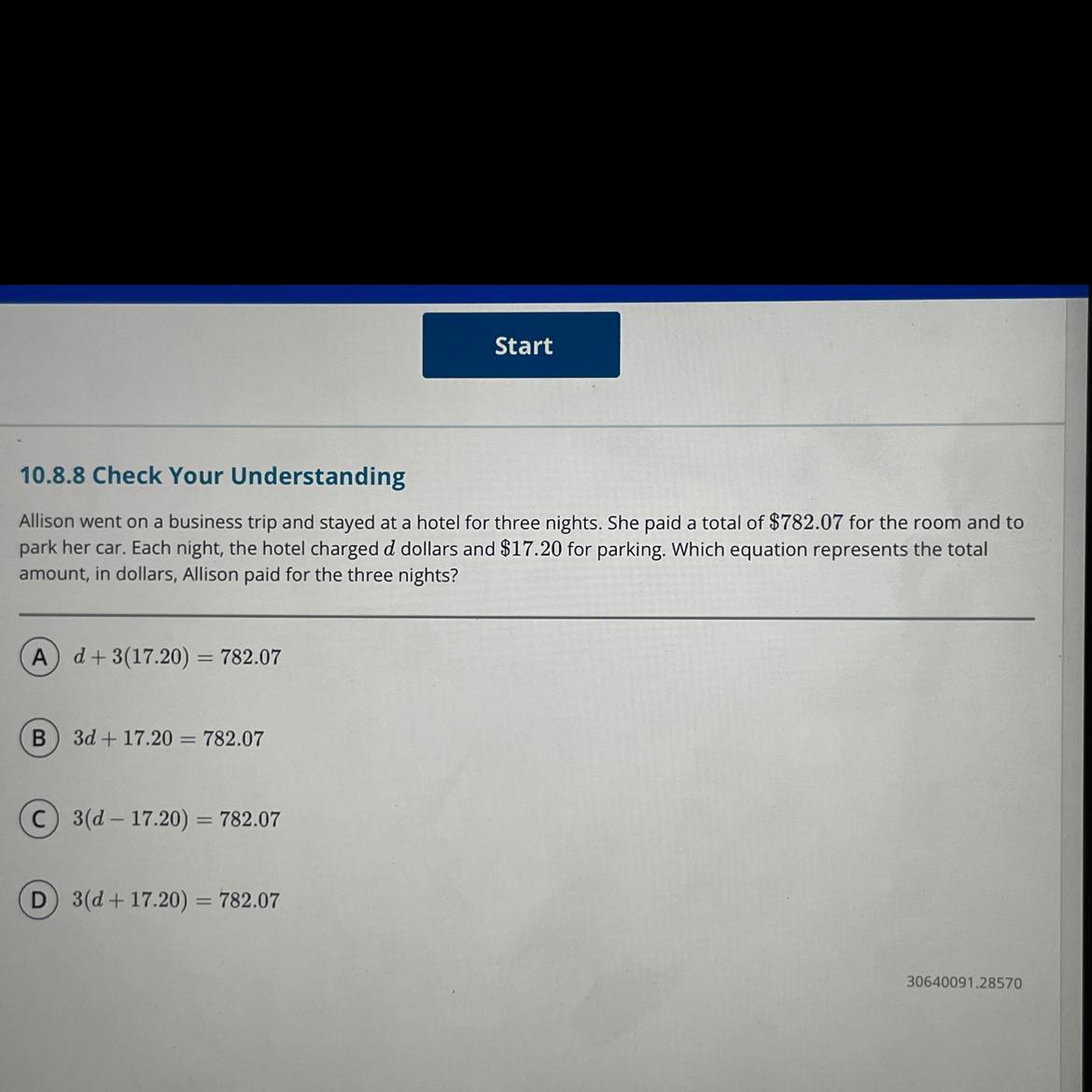
Answers
We can see that the correct equation that can depict the problem is 3(d+17.20) = 782.07. Option D
Which equation shows the total charge?We have to look at the problem that we have here. In the case of the question that we have been asked, we can see that for the problem that has been given here, it is clear that; Allison went on a business trip and stayed at a hotel for three nights. She paid a total of $782.07 for the room and to park her car.
If it is known that Each night, the hotel charged d dollars and $17.20 for parking. We can say that let the amount that is charged for the lodging be d and we have the equation as; 3(d+17.20) = 782.07.
Learn more about equation:https://brainly.com/question/29657983
#SPJ1
find the height of the tree

Answers
Use the property of similarity of triangles =》the corresponding sides of a triangle should be in the same ratio.
Take the missing side as 'x'.
The corresponding sides here are,
■ 7 & 14 ft
■ 5 & x ft
7/14 = 5/x
7x = 5 × 14 (cross multiplication)
7x = 70
x = 70/7
x = 10 ft
Height of the tree = 10 ft.
_____
Hope it helps ⚜
write the slope-intercept form of the equation of each line. (DONT do number 26 )

Answers
b: -1
Equation: -4x-1
27) m: 4
b: 4
Equation: 4x+4
28) m: 5/2 (or in decimals: 2.5)
b: 0
Equation: 5/2x or (2.5x)
Hoped this helped.
Answer:
25) -4, -1
Equation: -4x-1
27) 4, 4
Equation: 4x+4
29) 5/2,0
Equation: 5/2x
Step-by-step explanation:
Y=mx+b
A 13 km 13km13, start text, k, m, end text stretch of road needs repairs. Workers can repair 3 1 2 km 3 2 1 km3, start fraction, 1, divided by, 2, end fraction, start text, k, m, end text of road per week. How many weeks will it take to repair this stretch of road?
Answers
you can start by dividing the total length of the road by the distance that can be repaired per week:
13 km ÷ 3 1/2 km/week = 3.71 weeks
Rounding up, it will take 4 weeks to repair the entire 13 km stretch of road.
8.What side of the road will you see speed, yield, and guide signs on ?
Answers
Answer:
we see it in our left side of the road
Buster's dog house is 3 feet long, 2 feet wide, and 2 feet high. how much space would there be if buster's house were twice as long
Answers
there woldbe 96 volume
Step-by-step explanation:
to find the volume you have to multiply width x lenghth x height
so set up your equation like this -
3 x 2 x 2
the times everything by 2 so it will now look like this -
6 x 4 x 4
then solve and get the answer 96
the ortiz family is building a barn on a property with a perimeter of 120 meters. what is the area of the property that Mr. Ortiz is building the barn on?
Answers
Answer:
900 square meters
Step-by-step explanation:
The property is in the shape of a square.
The perimeter of a square is given as:
P = 4L
where L = length of its side
Therefore, the length of the property is:
120 = 4 * L
L = 120 / 4 = 30 meters
The area of a square is given as:
A = L * L
Therefore, the area of the property is:
A = 30 * 30 = 900 square meters
A bucket contains 72 red, 48 blue, 48 green, and 48 yellow crayons. The art teacher also has 120 pieces of drawing paper. What is the largest number of identical kits the art teacher can make with all of the crayons and all of the paper?
Answers
The art teacher can make a maximum of 24 identical kits using all the crayons and drawing paper for proper distribution.
To determine the largest number of identical kits the art teacher can make using all the crayons and drawing paper, we need to find the greatest common divisor (GCD) of the quantities.
The GCD represents the largest number that can divide all the quantities without leaving a remainder.
The GCD of the quantities of crayons can be found by considering the prime factorization:
72 = 2³ × 3²
48 = 2⁴ × 3
48 = 2⁴ × 3
48 = 2⁴ × 3
The GCD of the crayons is 2³ × 3 , which is 24.
Now, we need to find the GCD of the quantity of drawing paper:
120 = 2³ × 3 × 5
The GCD of the drawing paper is also 2³ × 3 , which is 24.
Since the GCD of both the crayons and drawing paper is 24, the art teacher can make a maximum of 24 identical kits using all the crayons and drawing paper.
Each kit would contain an equal distribution of crayons and drawing paper.
Learn more about distribution here:
brainly.com/question/30034780
#SPJ1
Consider the line 3x+2y=-1.
Find the equation of the line that is perpendicular to this line and passes through the point (5, 3).
Find the equation of the line that is parallel to this line and passes through the point (5, 3).
Note that the ALEKS graphing calculator may be helpful in checking your answer.
Equation of perpendicular line:
Equation of parallel line:
0
Answers
The given line is in the form Ax + By = C, where A = 3, B = 2, and C = -1. To find the slope of this line, we can rearrange the equation in slope-intercept form (y = mx + b), where m is the slope:
3x + 2y = -1
2y = -3x - 1
y = (-3/2)x - 1/2
The slope of the given line is -3/2. Since a line perpendicular to this line will have a negative reciprocal slope, we can find the perpendicular slope by taking the negative reciprocal of -3/2:
Perpendicular slope = -1 / (-3/2) = 2/3
Now we have the slope of the perpendicular line, and we can use the point-slope form of a line (y - y₁ = m(x - x₁)) to find its equation. Plugging in the values (5, 3) for (x₁, y₁) and 2/3 for m:
y - 3 = (2/3)(x - 5)
Expanding and simplifying:
3y - 9 = 2x - 10
2x - 3y = 1
Therefore, the equation of the line that is perpendicular to 3x + 2y = -1 and passes through the point (5, 3) is 2x - 3y = 1.
To find the equation of a line parallel to the given line and passing through the point (5, 3), we can use the same method. Since parallel lines have the same slope, the slope of the parallel line will also be -3/2.
Using the point-slope form with (5, 3) and -3/2:
y - 3 = (-3/2)(x - 5)
Expanding and simplifying:
2y - 6 = -3x + 15
3x + 2y = 21
Therefore, the equation of the line that is parallel to 3x + 2y = -1 and passes through the point (5, 3) is 3x + 2y = 21.
The lengths of bolts in a batch are distributed normally with a mean of 3 cm and a standard
deviation of 0.04 cm.
What is the probability that a bolt has a length greater than 2.96 cm?
Answers
Answer:
0.8413 = 84.13% probability that a bolt has a length greater than 2.96 cm.
Step-by-step explanation:
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Mean of 3 cm and a standard deviation of 0.04 cm.
This means that \(\mu = 3, \sigma = 0.04\)
What is the probability that a bolt has a length greater than 2.96 cm?
This is 1 subtracted by the p-value of Z when X = 2.96. So
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{2.96 - 3}{0.04}\)
\(Z = -1\)
\(Z = -1\) has a p-value of 0.1587.
1 - 0.1587 = 0.8413
0.8413 = 84.13% probability that a bolt has a length greater than 2.96 cm.
At 6 A.M. the temperature was -5 degrecs Celsius. In the afternoon, the temperature was 10 degrees Celsius. What was the change of temperature during the day?
Answers
The change in temperature is just the difference of the temperature
\(10-(-5)\text{ = 10+5=15}\)So, the temperature has changed 15 degrees Celsius during the day.
working on Rates with fraction's, how many steps did he average per minute?Robert climbed 775 steps in 12 and 1/2 minutes
Answers
Answer:
62 steps per minute
Explanation:
Let the number of steps he climbed per minute be x.
If Robert climbed 775 steps in 12 and 1/2 minutes, let's go ahead and determine many steps he took per minute by setting up the question as a proportion;
\(\begin{gathered} \frac{775\text{ steps}}{12.5\text{ minutes}}=\frac{x\text{ steps}}{1\text{ minute}} \\ 12.5x=775 \\ x=\frac{775}{12.5} \\ x=62\text{steps} \end{gathered}\)Find the value of x, 6,4, 3x, 4x+1

Answers
Answer:
If two chords intersect in a circle, then the product of the segments of one chord equals the product of the segments of the other chord.
6(3x) = 4(4x + 1)
18x = 16x + 4
2x = 4
x = 2
absolute value of 7 and one
eigth
Answers
Please give brainliest❤️
Solve Logaritmic equation
log16x=3/2
Answers
To solve for x in the equation log(16x) = 3/2, we need to use the definition of logarithms, which states that log base b of a is equal to c if and only if b raised to the power of c equals a.
In this case, we have:
log(16x) = 3/2
Rewriting this in exponential form, we get:
10^(3/2) = 16x
We can simplify 10^(3/2) as follows:
10^(3/2) = 10^(1/2) * 10^1 * 10^(1/2) = (sqrt(10))^2 * 10^(1/2) = 10 * sqrt(10)
Therefore, we have:
16x = 10 * sqrt(10)
Dividing both sides by 16, we get:
x = (10 * sqrt(10)) / 16
Simplifying this expression, we get:
x = (5 * sqrt(10)) / 8
So the solution to the equation log(16x) = 3/2 is x = (5 * sqrt(10)) / 8.
Workings please......

Answers
Answer:
21.142
Step-by-step explanation:
not sure it's correct

SLOPE DIGITAL ESCAPE ROOM
I need help finding the code

Answers
By finding all the four slopes, we can see that the word is ECHA.
How to find the word?We know that the general linear equation can be written as:
y = a*x + b
Where a is the slope and b is the y-intercept.
We know that if the line passes through (x₁, y₁) and (x₂, y₂) then the slope is:
s = (y₂ - y₁)/(x₂ - x₁)
With that formula we can get the slopes.
1) Using the points (0, 3) and (2, 4).
m = (4 - 3)/(2 - 0) = 1/2, so the letter is E.
2)Using (-1, -12) and (1, -8)
m = (-8 + 12)/(1 + 1) = 4/2 = 2, so the letter is C.
3) We have (2, -6) and (-4, -3) so:
m = (-3 + 6)/(-4 - 2) = 3/-6 = -1/2, so the letter is H
4)we can use the points (0, 3) and (1, 1), so:
m = (1 - 3)/(1 - 0) = -2, so the letter is A
Then the word is ECHA
Learn more about slopes at:
https://brainly.com/question/3493733
#SPJ1
⅓÷4=n
nonses=REPORT
Answers
Answer:
n=1/12Step-by-step explanation:
1/3:4=n
1/3*1/4=n
n=1/12
-----------------------
check
1/3:4=1/12
1/3*1/4=1/12
1/12=1/12
The answer is good
- The area of a rectangle can be found by using A
24w + w2, where w represents the
width. What is the width of the rectangle when the area is 3456 in.2 ?
Answers
Answer:
26w
Step-by-step explanation:
Please help! Will give brainiest if correct

Answers
Answer:
Step-by-step explanation:
First Choice
Calculate the % loss
Cost price of an article =$28
Selling price of the article=$21
Answers
The loss in percentage is 25%.
Given that,
Cost price of an article = $28
Selling price of the article = $21
We know that,
A figure or ratio that may be stated as a fraction of 100 is a percentage. If we need to calculate a percentage of a number, we should divide it by its entirety and then multiply it by 100.
The proportion therefore refers to a component per hundred. Per 100 is what the word percent means. The letter "%" stands for it.
Now loss can be calculated by subtracting selling price from cost price,
Therefore,
28 - 21 = 7
Hence there are loss of $7 in business,
Now to calculate percentage loss,
Divide loss by cost price then multiply with 100,
Then,
⇒ (7/28)x100
⇒ 25%
Learn more about the percent visit:
https://brainly.com/question/24877689
#SPJ2
A board, 66 cm long is cut into three pieces such that the second piece is twice as long as the first and the
third is 6 cm longer than the second.
Find the length of the shorter piece.
cm
Answers
100 points!!!
Solve the following equation:
8x + 3 = 2x + 9
Answers
Answer:
\(\Huge \boxed{\boxed{ x = 1}}\)
Step-by-step explanation:
Isolate the variable on one side of the equation before trying to solve it. It means that you should only have constants (numbers) on the other side of the equal sign and the variable alone on the one side.
To do this, you can add, subtract, multiply, divide, or use any other operation to both sides of the equation as long as you do the same thing on both sides.
Your final step depends on the equation and how you've simplified it. In general, you want to figure out how you arrived at the final equation by working backwards from it. You'll isolate the variable in the last action you took.
-------------------------------------------------------------------------------------------------------------
SolutionStep1: Subtract \(\bold{2x}\) from both sides
\(8x + 3 = 2x + 9\)\(8x - 2x + 3 = 2x - 2x + 9\)\(6x + 3 = 9\)Step 2: Subtract 3 from both sides
\(6x + 3 - 3 = 9 - 3\)\(6x = 6\)Step 3: Divide both sides of the equation by 6
\(\frac{6x}{6} = \frac{6}{6}\)\(x = 1\)So the solution to the equation \(\bold{8x + 3 = 2x + 9}\) is \(\bold{x = 1}\).
-------------------------------------------------------------------------------------------------------------
x f(x) f ′(x) g(x) g′(x)
2 5 1 2 1
4 −2 −6 5 4
5 1 2 4 5
6 5 1 2 −2
The functions f and g have continuous derivatives. The table gives values of f, f ′, g, and g′ at selected values of x.
Part A: Find h′(2) if h(x) = g(f(x)). (5 points)
Part B: Find m′(2) if m(x) = f(x2). (5 points)
Part C: Let k(x) = f(g(x)). Write an equation for the line tangent to the graph of k at x = 4. (10 points)
Part D: Let j of x is equal to g of x divided by f of x. Find j′(2). (10 points)

Answers
Answer:
A. h'(2) = 5
B. m'(2) = -24
C. y = 8x - 31
D. j'(2) = 3/25 = 0.12
Step-by-step explanation:
When differentiating composite functions, use the chain rule.
\(\boxed{\begin{minipage}{5.4 cm}\underline{Chain Rule for Differentiation}\\\\$\left[f\left(g(x)\right)\right]'=f'\left(g(x)\right) \cdot g'(x)$\\\end{minipage}}\)
Chain Rule: The derivative of a composite function is the product of the derivative of the outer function evaluated at the inner function and the derivative of the inner function.
Part AUsing the chain rule, if h(x) = g(f(x)) then h'(x) = g'(f(x)) ⋅ f'(x).
To find h'(2), substitute x = 2 into the differentiated equation:
\(\begin{aligned}h'(x)& = g'(f(x)) \cdot f'(x)\\\\\implies h'(2)& = g'(f(2)) \cdot f'(2)\\& = g'(5) \cdot 1\\& = 5 \cdot 1\\&=5\end{aligned}\)
Therefore, h'(2) = 5.
Part BUsing the chain rule, if m(x) = f(x²) then m'(x) = f'(x²) ⋅ 2x.
To find m'(2), substitute x = 2 into the differentiated equation:
\(\begin{aligned}m'(x) &= f'(x^2) \cdot 2x\\\\\implies m'(2) &= f'(2^2) \cdot 2(2)\\&=f'(4) \cdot 4\\&=-6 \cdot 4\\&=-24\end{aligned}\)
Therefore, m'(2) = -24.
Part CTo find the slope of the tangent line to the graph of k at x = 4, substitute x = 4 into the derivative of k(x).
If k(x) = f(g(x)) then k'(x) = f'(g(x)) ⋅ g'(x).
Therefore, the slope of the tangent line is:
\(\begin{aligned}k'(x) &= f'(g(x)) \cdot g'(x)\\\\\implies k'(4) &= f'(g(4)) \cdot g'(4)\\&= f'(5) \cdot 4\\&= 2 \cdot 4\\&= 8\end{aligned}\)
Now calculate k(x) when x = 4:
\(\begin{aligned}k(x)&=f(g(x))\\\\\implies k(4) &= f(g(4))\\&=f(5)\\&=1\end{aligned}\)
To write the equation of the tangent line, substitute the found slope m = 8 and point (4, 1) into the point-slope equation:
\(\begin{aligned}y-y_1&=m(x-x_1)\\y-1&=8(x-4)\\y-1&=8x-32\\y&=8x-31\end{aligned}\)
Therefore, an equation for the line tangent to the graph of k at x = 4 is:
y = 8x - 31Part DTo find the derivative of j(x) use the quotient rule.
\(\textsf{If\;\;$j(x)=\dfrac{g(x)}{f(x)}$\;\;then:}\\\\\\j'(x)=\dfrac{f(x)g'(x)-g(x)f'(x)}{(f(x))^2}\)
To calculate j'(2), substitute x = 2 into the equation:
\(\begin{aligned} \implies j'(2)&=\dfrac{f(2)g'(2)-g(2)f'(2)}{(f(2))^2}\\\\&=\dfrac{5 \cdot 1-2 \cdot 1}{(5)^2}\\\\&=\dfrac{5-2}{25}\\\\&=\dfrac{3}{25}\\\\&=0.12\end{aligned}\)
Therefore, j'(2) = 3/25 = 0.12.