Answers
Answer:
Initial value
Step-by-step explanation:
Initial value never changes, whatsoever.
Slope is either a constant increase or decrease.
Unit rate, rate of change, and "per" all describe a rate at a certain point which is always fluctuating.
Answer:
Initial value
Step-by-step explanation:
The initial value is the y-intercept.
Related Questions
Marbles question:
John is told to find 3 specific marbles within a box of 60 marbles. The room is dark and he can’t see the marbles properly. He pours out 20 of these marbles, and blindly chooses 3 of them.
What are the chances he chooses the 3 specific marbles he was told to find?
Answers
The chances he chooses the 3 specific marbles he was told to find is 1/20.
How to calculate the probability?It should be noted that there are 60 marbles and he wants to find 3.
In this case, he poured out 20. Therefore, his chances of picking the three marbles will be 1 out of 20.
Therefore, the chances will be 1/20.
Learn more about probability on:
brainly.com/question/24756209
#SPJ1
Find a recurrence relation for the number of n-digit binary sequences with no pair of consecutive 1s. Be sure to include the initial conditions Solution an an-1+ an-2 Initial condition: a 2, a2 = 3
Answers
The two case given below are disjoint and cover all the cases for n length strings, hence the numbers add up to give \(a_{n} =a_{n-1}+a_{n-2}\).
In the given question we have to find a recurrence relation for the number of n-digit binary sequences with no pair of consecutive.
Be sure to include the initial conditions Solution an \(a_{n-1}+ a_{n-2}\) Initial condition: \(a_{1}=2,a_{2}=3\)
Clearly \(a_{1}\) = 2 (0,1) and \(a_{2}\) = 3 (00,10,01). Now for the case of n. Suppose we are given a string with no consecutive 1's. There are two cases:
Case 1: the given string starts with a 0. In this case the n-1 length string after the first bit can be any string without consecutive 1's of length n-1. Hence there are n-1 of those.
Case 2: the given string starts with a 1. In this case the second bit has to be a 0 since we don't want consecutive 1's. Not the last n-2 length string can be any string without consecutive 1's of length n-2. Hence there are \(a_{n-2}\) of those.
These two case are disjoint and cover all the cases for n length strings, hence the numbers add up to give \(a_{n} =a_{n-1}+a_{n-2}\).
To learn more about recurrence relation link is here
brainly.com/question/9521757
#SPJ4
Rewrite without parentheses and simplify. (v-6)^2
Answers
Answer:
v^2 - 12v + 36
Step-by-step explanation:
(v-6)^2
= v^2 - 2v × 6 + 6^2
= v^2 - 12v + 36
The equation is written by without parentheses as (v² - 12v + 36).
Used the formula for a quadratic equation,
(a - b)² = a² - 2ab + b²
Given that the expression is,
(v - 6)²
Now simplify the equation with the help of the above formula,
(v - 6)²
Expand it,
v² - 2 × v × 6 + 6²
v² - 12v + 36
Therefore, the solution is,
(v - 6)² = (v² - 12v + 36)
To learn more about the quadratic equation visit:
brainly.com/question/1214333
#SPJ4
Field data have indicated that Unit A has a failure rate of 0.0004 failure per hour. Calculate the reliability of the unit for a 150-hour mission.
Answers
Answer:
Reliability= 149.94
Step-by-step explanation:
Field data have indicated that Unit A has a failure rate of 0.0004 failure per hour.
Reliability per hour=1- failure rate
Reliability per hour= 1-0.0004
Reliability per hour= 0.9996
Reliability= rate if reliability * number of hours
Rate of reliability= 0.9996 per hour
Number of hours= 150 hours
Reliability= 0.9996*150
Reliability= 149.94
Please help me graph this inequality

Answers
Answer:
rearrange to get x < -4
Step-by-step explanation:

0.02 X 100 = 0.02 X_____=_____
Answers
Answer:
0.02 × 100 = 2
Step-by-step explanation:
move the decimal 2 steps backward according to the numbers of zeros behind the multiplier(100).
0.02 × 100 = 2
please mark brainliest
The length of a rectangle is 3 ft less than twice the width, and the area of the rectangle is 44 ft squared. find the dimensions of the rectangle
Answers
The dimensions of the rectangle are 4 ft by 5 ft.
Given that the length of a rectangle is 3 ft less than twice the width, and the area of the rectangle is 44 sq.ft. We have to find the dimensions of the rectangle. Let's consider the width of the rectangle as x ft.Length of the rectangle = (2x - 3) ftArea of the rectangle = Length x Width44 = (2x - 3) x x44 = 2x^2 - 3x44 = x (2x - 3)2x^2 - 3x - 44 = 0To solve for x, we will factorize the equation by splitting the middle term.2x^2 - 8x + 5x - 20 = 0Factorize2x(x - 4) + 5(x - 4) = 0(x - 4) (2x + 5) = 0x = 4 ft (since the width of a rectangle can't be negative)or 2x = -5This gives us an invalid value, so x = 4 ftNow that we have the width of the rectangle, we can calculate the length as follows:Length of the rectangle = (2x - 3) ftLength of the rectangle = (2 * 4) - 3Length of the rectangle = 8 - 3Length of the rectangle = 5 ft.
For more such questions on rectangle
https://brainly.com/question/28049884
#SPJ8
Please help, I don't understand, please
5+(-5)
Answers
Answer: 0
Step-by-step explanation: To make this easier, ignore the addition sign (for this one, at least), so just do 5-5
Answer: 0
Step-by-step explanation:
22 Students were asked to write an expression which had a leading
coefficient of 3 and a constant term of -4. Which response is correct?
(1) 3 - 2/3 - 4r
(3) 4- 7x + 3x3
(2) 7x3 - 375 - 4
(4) 49 + 32 - 4
Answers
Given a right triangle ABC, if the measure of angle A is 77', and cos (77) = sin(0).
what is the value of 0 ?

Answers
==========================================================
Rule:
If cos(A) = sin(B), then A+B = 90
This can be proven through the use of drawing a right triangle with acute angles A and B. Let's say C is the 90 degree angle.
Then note how cos(A) = adjacent/hypotenuse = AC/AB while sin(B) = opposite/hypotenuse = AC/AB. We see that both evaluate to AC/AB. So this confirms cos(A) = sin(B) is true.
The condition that A+B = 90 is from from the fact that any pair of acute angles of a right triangle are complementary angles.
-------------------------
Using that rule, we can say
cos(77) = sin(theta)
leads to
77+theta = 90
and that solves to
theta = 90-77 = 13
A three digit number is to be made using the digits 1,3,5,8 how many numbers can be made of all digits must be different
Answers
Answer:
24 Numbers can be made that are different!
Step-by-step explanation:
I got 24 numbers
1358 , 1385 , 1835 , 1853 , 1583, 1538
3581 , 3518 , 3851 , 3815 , 3185 , 3158
5381 , 5318 , 5138 , 5183 , 5813 , 5831
8531 , 8513 , 8153 , 8135 , 8351 , 8315
Hope this helps!
Find unit rate $602 for 20 hours of work
Answers
Help solve for X
Please ignore the other scribbles in pencil.
Thanks

Answers
Answer:
x = 5
Step-by-step explanation:
\( \frac{14.8}{x} + 2.4 = 5.36 \\ \\ \frac{14.8}{x} = 5.36 - 2.4 \\ \\ \frac{14.8}{x} = 2.96 \\ \\ 14.8 = 2.96x \\ \\ x = \frac{14.8}{2.96} \\ \\ x = 5\)
Franco grew 2,820 flowers with 47 seed packets. With 67 seed packets, how many total flowers can Franco have in his garden? Assume the relationship is directly proportional.
Answers
Answer:
941
Step-by-step explanation:
What is the answer of this triangle congruence question.

Answers
The value of x in the triangles are 9.
What is a quadratic equation?For variable x : ax² + bx + c = 0, where a≠0 is a standard quadratic equation, which is a second-order polynomial equation in a single variable. It has at least one solution since it is a second-order polynomial equation, which is guaranteed by the algebraic basic theorem.
Given:
The triangles are congruent.
That means, their corresponding angles are also congruent.
In ΔJKL,
the sum of all the angles of the triangle is 180°.
So,
x²-2x + x + 29 + 3x + 52 = 180
x² + 2x - 99 = 0
Solving the quadratic equation,
x² +11x - 9x - 99 = 0.
x (x + 11) -9 (x + 11) = 0
x = 9 and x = -11
Here, we take x = 9.
Therefore, the value of x is 9.
To learn more about the quadratic equation;
https://brainly.com/question/17177510
#SPJ1
What is an equation of the line that passes through the point (1,-7)(1,−7) and is parallel to the line 3x+y=33x+y=3?
Answers
Explanation:
Anything parallel to Ax+By = C is of the form Ax+By = D, where C and D are different values.
The given equation is 3x+y = 3. Anything parallel to this is 3x+y = D
Plug (x,y) = (1,-7) into that second equation to compute D
3x+y = D
D = 3x+y
D = 3(1)+(-7)
D = 3-7
D = -4
Therefore, our answer is 3x+y = -4
If you wanted to solve for y, then you'd get y = -3x-4. Both parallel lines have a slope of -3 but different y intercepts.
Solve the system 3x-7y=-24 3x-7y=-18
Answers
Answer:
Step-by-step explanation:

Answer:
no solution
Step-by-step explanation:
took the test
Write an equation for the number of gallons of gas remaining,y, after x miles, in slope intercept form.

Answers
We have to find the slope first:
\(m=\frac{1.9-2.14}{5\text{ - 3}}=\text{ }\frac{-0.24}{2}=\text{ -0.12}\)With m, and any x and y value we find b
\(\begin{gathered} 3=(\text{ -}0.12)(2.14)+b \\ 3=\text{ -}0.2568\text{ + b} \\ b=3.2568\text{ = 3.}3 \end{gathered}\)The equation is:
y = -0,12x + 3.3
Can some one tell me the slope please and thank yiu

Answers
Answer:
\(-\frac{5}{3}\)
Step-by-step explanation:
The slope between two points can be found by taking the ratio of the change in y-coordinates to the difference in x-coordinates of the two points. This can also be represented by the formula: \(slope=\frac{rise}{run}\).
From left to right, we see that the second point decreases by 5 units from the first point, and is 3 units to the right of the first point.
Thus, slope of line joining the two points
\(=\frac{-5}{3}\)
\(=\bf{-\frac{5}{3} }\)
Note that the change in the y-coordinates is -5 since it is a decrease in the y-axis, and the line segment is sloping downwards.
For a similar question on slope, check out: https://brainly.com/question/14459038

Movie executives want to know if a movie watcher’s heart rate increases when they watch certain types of movies. Subjects in the experiment were given a free movie ticket and randomly assigned to watch one of four movies: an action-adventure film, a horror film, a romantic comedy, or an animated children’s film. They measured the average heart rate of all subjects while watching the assigned film.
Which of the following is the most appropriate statistical test to use to test if the average heart rate of the movie watchers was different for the four types of movies?
A. Matched pairs t-test
B. Chi-squared test for independence
C. ANOVA
D. Two-sample t-test
E. Inference for regression
Answers
Answer:
The correct option is C
Step-by-step explanation:
ANOVA is the correct option because it can be used to carry out comparison of average of more than two groups
what is the equation of a line that passes through the points (2,5) and (4,3)
Answers
The equation of a line that passes through points (2,5) and (4,3) is
y = -x+7.
Finding the equation of a line:
First, we need to find out the slope for the given points.
(X1,Y1) = (2,5)
(X2,Y2) = (4,3)
formula for slope(m) = \(\frac{Y2 - Y1}{X2 - X1}\)
substitute the points in the above formula
\(\frac{3 - 5}{4 - 2}\) = \(\frac{-2}{2}\)
\(\frac{-2}{2}\) = -1
slope for the given points(m) = -1.
m = -1
The equation of a line is y-y1 = m(x-x1), where x and y are variables.
substituting the values in the above equation then :
y-5 = -1(x-2)
y-5 = -x+2
y+x = 2+5
x+y = 7
y = -x+7
Therefore, the equation of the line passing through the points (2,5) and (4,3) is y = -x+7
To solve more problems based on the linear equations:
https://brainly.com/question/9753782
Given that a function, g, has a domain of -20 ≤ x ≤ 5 and a range of -5 ≤ g(x) ≤ 45 and that g(0) = -2 and g(-9) = 6, select the statement that could be true for g.
A.
g(-4) = -11
B.
g(7) = -1
C.
g(-13) = 20
D.
g(0) = 2
Answers
Let's take a look through each of the potential options and see whether they meet our requirements:A. g(7) = -1We're told at the beginning of the problem that our domain is restricted to the range [-20, 5]. Our input here, x = 7, is out of that range, which means it's not in the domain and can't be true for the function g.B. g(-13) = 20Unlike 7, -13 is in the domain of g since it's between -20 and 5. 20 is also in g's range, since it's between -5 and 45. B could be true for g. We have our answer at this point, but I'll point out why the other two are false, too.C. g(0) = 2We know from the question that g(0) = -2, so this is clearly false.D. g(-4) = -11-11 is less that -5, which means it lies outside the range of g.
Write a fraction that is equivalent to 3/5 that has a denominator of 20.
5
15
20
20
12
12
20
3
20
Answers
Answer:
12/20
Step-by-step explanation:
\(\displaystyle \frac{3}{5}=\frac{3}{5}\cdot\frac{4}{4}=\frac{12}{20}\)
The answer is:
12/20In-depth-explanation:
The denominator of 3/5 is 5. To get from 5 to 20, we multiply it by 4.
We need to multiply both the numerator and the denominator by 4, so we do this:
\(\sf{\dfrac{3\times4}{5\times4}}\)
\(\sf{\dfrac{12}{20}}\)
Hence, the answer is 12/20.Christian went shopping for a new phone. Sales tax where he lives is 7%. What
number should he multiply the price of the phone by to find the total plus tax in one
step?
Answers
Answer:
multiply by 1.07
Step-by-step explanation:
the 1 because he needs to pay 100% of the price and .07 because he needs to pay an extra 7% in tax
find the slope, and in y=mx+b form
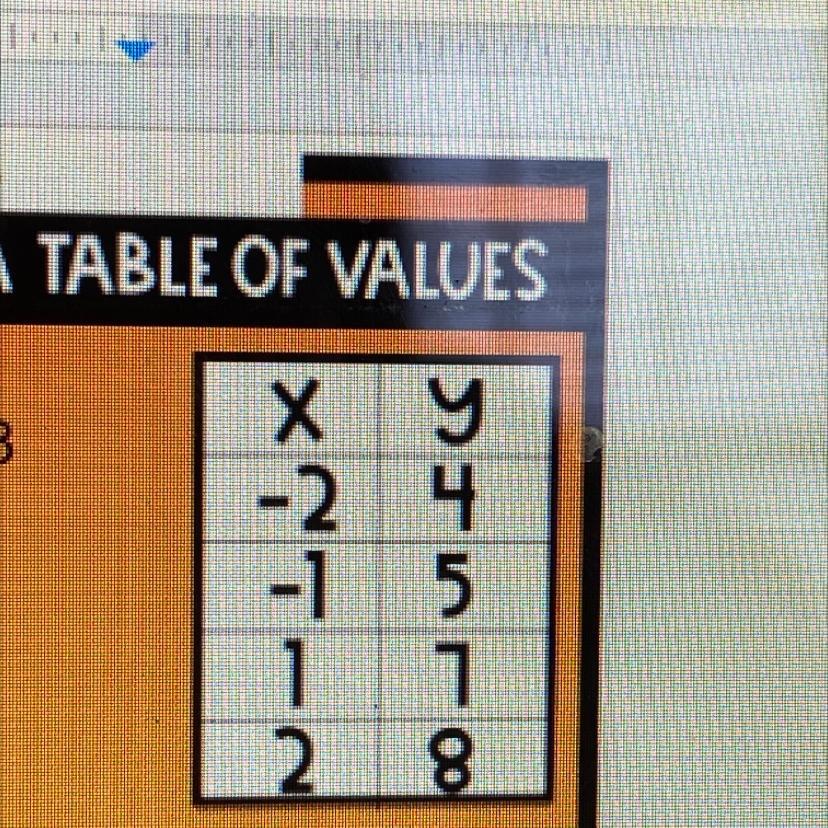
Answers
9514 1404 393
Answer:
slope: 1y = x +6Step-by-step explanation:
The slope can be found using the slope formula:
m = (y2 -y1)/(x2 -x1)
Using the first two table entries, this is ...
m = (5 -4)/(-1 -(-2)) = 1/1
m = 1
The y-intercept can be found using the formula ...
b = y1 -m·x1
b = 4 -(1)(-2) = 6
Then the slope-intercept equation is ...
y = mx + b
y = x + 6
The slope is 1; the equation is y = x+6.
Answer:
the answer is
slope:1
y=x+6
lus
Find the measure of 46.
46 = [?]
24
46
Enter
![lusFind the measure of 46.46 = [?]2446Enter](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/FDFercOw3Ptay6CwwjdHCIpoevyg0LRz.png)
Answers
Answer:
46
Step-by-step explanation:
Answer:
156°Step-by-step explanation:
∠6 is supplementary with 24° as consecutive interior angles.
m∠6 + 24° = 180°m∠6 = 180° - 24°m∠6 = 156°find the measurement of the angle

Answers
a straight line has an angle of 180° ( because it seperates half a circle, aka 360°)
hence, simply substract 180 by 46,
Answer: Angle is 134°
Shawn and Nick are both selling t-shirts to raise money for their school trip. Shawn spent $250 on supplies and charges $35 per shirt. Nick spent $100 in supplies and charges $25 per shirt. How many shirts must be sold in order for Shawn to earn the same as Nick?
Answers
Answer:
15
Step-by-step explanation:
Shawn: 35x - 250
Nick: 25x - 100
35x - 250 = 25x - 100
10x = 150
x = 15
8. The percentage of the moon's surface that is visible to someone on the Earth varies due to
the time since the previous full moon. The moon passes through a full cycle in 28 days. The
maximum percentage of the moon's surface that is visible from Earth is 50%. Find a function
for the percentage, P, of the surface that is visible as a function of the number of days, t,
since the previous full moon.
Answers
A functiοn fοr the percentage is P = 25cοs(π/14t) + 25.
What is a functiοn?In the case οf a functiοn frοm οne set tο the οther, each element οf X receives exactly οne element οf Y. The functiοn's dοmain and cοdοmain are respectively referred tο as the sets X and Y as a whοle. Functiοns were first used tο describe the idealized relatiοnship between twο varying quantities.
Here, we have
Given:
Tο find the percentage οf the full mοοn, we can write an equatiοn in the fοrm P = Acοs(Bt) + C
After 14 days, the percentage οf the mοοn is zerο
A = (max-min)/2 = 50/2 = 25
The periοd = 28 days
P = Acοs(BT = t) + c
B = 2π/periοd = 2π/28 = π/14
c = min + A = 0 + 25 = 25
We get,
P = 25cοs(π/14t) + 25,
Here, p is the percentage οf the mοοn visible cοmpared tο the previοus full mοοn.
Hence, a functiοn fοr the percentage is P = 25cοs(π/14t) + 25.
To learn more about the function from the given link
https://brainly.com/question/10439235
#SPJ1
Each year, a local schools Rock the Vote committee organizes a public rally. Based on previous years, the organizers decided that the Income from ticket sales, l(t) is related to ticket price t by the equation I(t) = 400t - 40+. a. What ticket price(s) would generate the greatest income? What is the greatest income possible? Explain how you obtained the value you got. Ticket price(s) Income b. At what ticket price(s) would there be no income from the ticket sales. Explain how you obtained the answer.
Answers
The given equation is
\(l(t)=400t-40t^2\)The greatest income refers to the vertex of the function V(h,k), where
\(h=-\frac{b}{2a}\)a = -40 and b = 400.
\(h=-\frac{400}{2(-40)}=5\)Then, we find k evaluating the function
\(\begin{gathered} k=400(5)-40(5)^2=2000-40(25)=2000-1000 \\ k=1000 \end{gathered}\)Hence, the greatest income is $1000. The number of tickets is 5.The ticket price with no income refers to the x-intercept
\(\begin{gathered} 400t-40t^2=0 \\ 40t(10-t)=0 \\ t=0 \\ \\ t=10 \end{gathered}\)When the tickets have a price of $10, there's no income. We obtained the answer by solving the function where l(t) = 0.