Which can be proven? Select all that apply.
A. ∠ C E D ≅ ∠ A H J
B. A B ≅C B
C. C B ≅D B
D. ∠ D A G ≅ ∠ J C F
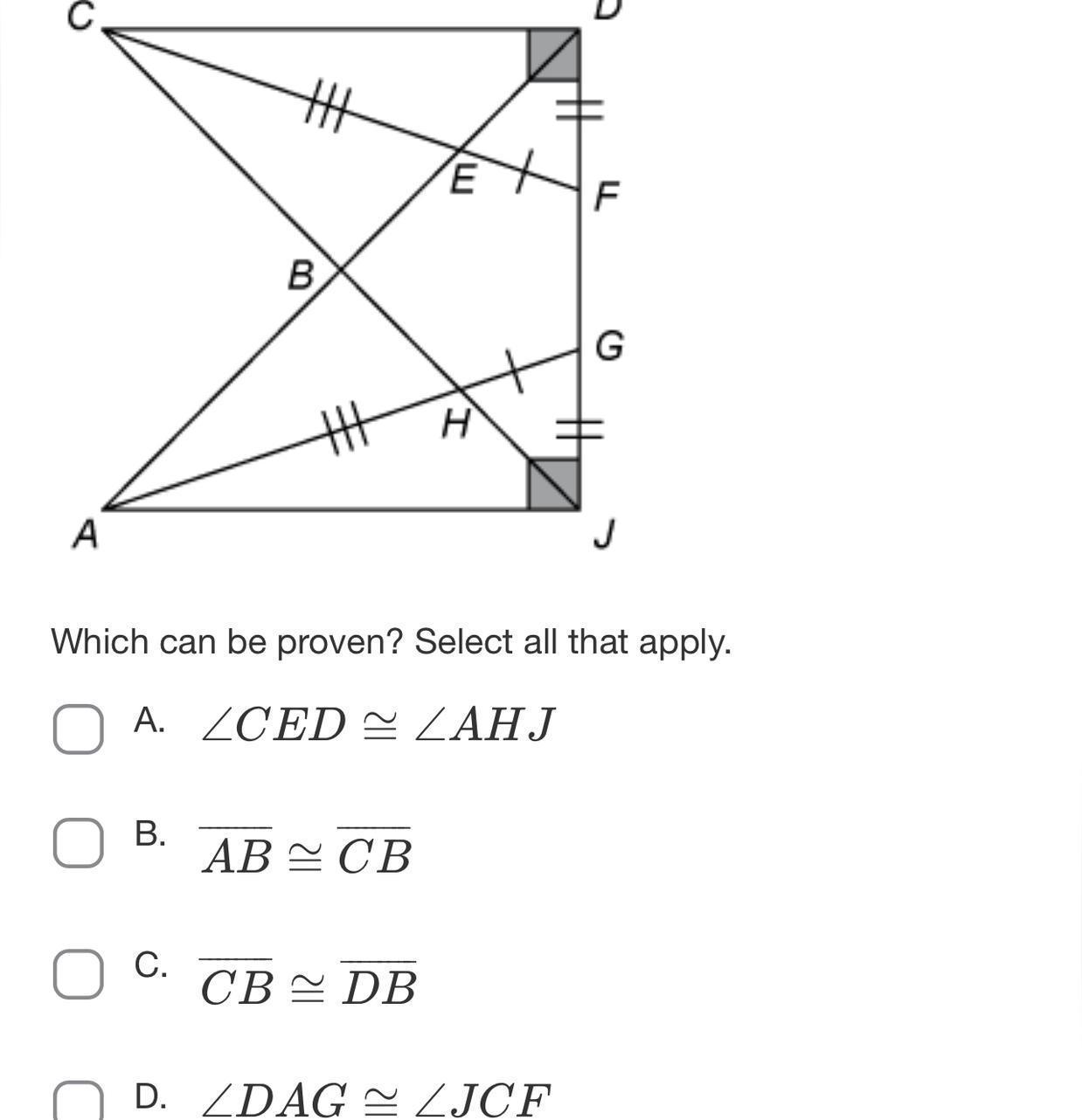
Answers
The Option that can be proven is:
∠ C E D ≅ ∠ A H J (Option A) The principle at play here is that ∠CDJ and ∠AJD are both right-angled triangles, (given)LInes CF and AG are congruent (given)Distance between Line AH and LInes CE are congruent (given), hence, ∠ C E D ≅ ∠ A H J.What is mathematical proof?Definitions, assertions, and methods are linked in a proper fashion to get the desired outcome in mathematical proof.
This procedure helps pupils understand the rationale behind the statement. This is also true of counterexamples and their important significance in mathematics.
Learn more about Mathematical Proof:
https://brainly.com/question/13259961
#SPJ1
Related Questions
What two numbers add to 29 and multiply to 28
Answers
This is because 1 x 28 = 28 and 1 + 28 = 29.
the equation below represents the total price of Michigan State University per semester where c represents the number of classes and t represents the total cost for the semester including a one time fee for room and board
Answers
The equation that represents the total price of Michigan State University per semester is determined by the number of classes taken (c) and the total cost for the semester, which includes a one-time fee for room and board (t).
The equation captures the relationship between these variables and calculates the overall cost for a student attending the university. It is important to note that the equation provides a quantitative representation and does not take into account other factors such as scholarships, financial aid, or additional expenses. Therefore, the equation serves as a useful tool for estimating the total cost of attending Michigan State University, allowing students and their families to plan and budget accordingly for their education.For such more question on equation
https://brainly.com/question/29174899
#SPJ8
What is the range of y= sec-'(x)? PreCal, send help please!!

Answers
Given:
The function is:
\(y=\sec^{-1}(x)\)
To find:
The range of the given function.
Solution:
We have,
\(y=\sec^{-1}(x)\)
The range of secant inverse function is:
\(Range=\{y|0\leq y\leq \pi , y\neq \dfrac{\pi}{2}\}\)
The range of the given function in interval notation is:
\(Range=\left[0,\dfrac{\pi}{2}\right)\text{ and }\left( \dfrac{\pi}{2}, \pi\right ]\)
Therefore, the correct option is C.
how do I find the inverse of this function??

Answers
The inverse function of f(n) is:
g(n) = -(4/7)*n - 8/7
How to find the inverse of the function?Two functions are inverses if the composition is equal to the identity, so if g(n) is the inverse of f(n), we must have that:
f( g(n) ) = n
Replacing the actual function we will get:
-2 - (7/3)*g(n) = n
Now we can solve this for the inverse function g(n), then we will get:
-2 - (7/3)*g(n) = n
(-7/4)*g(n) = n + 2
g(n) = (-4/7)*(n + 2)
g(n) = -(4/7)*n - 8/7.
That is the inverse function.
Learn more about inverses at:
https://brainly.com/question/3831584
#SPJ1
Sixty-nine percent of U.S heads of household play video or computer games. Choose 4 heads of household at random. Find the probability that none play video or computer games.
Answers
Answer: 0.00923521
Step-by-step explanation:
Given : The probability U.S households play video or computer games=69%=0.69
here, the probability of each U.S household play video or computer games is fixed as 0.69
Then, the probability of each U.S household not play video or computer games= 1-0.69=0.31
For independent events the probability of their intersection is product of probability of each event.
Now, the probability that none play video/computer games will be :-
\((0.31)^4=0.00923521\)
Solve each of the quadratic equations.
0 = 5x2 - 2x + 6
Answers
Please help!! Thank you!

Answers
Using angle relationships, the missing measures are:
m<3 = 138 degrees.
m<5 = 42 degrees.
m<8 = 138 degrees.
How to Find the Missing Angles?Using angle relationships, each of the measure of the angles can be calculated as follows:
Given that, m<1 = 138 degrees.
m<3 = m<1 [vertical angles are congruent]
Substitute:
m<3 = 138 degrees.
m<5 + m<3 = 180
Substitute:
m<5 + 138 = 180
m<5 = 180 - 138
m<5 = 42 degrees.
m<8 = m<3 [alternate interior angles are congruent]
m<8 = 138 degrees.
Learn more about missing angles measure on:
https://brainly.com/question/29115116
#SPJ1
using the given quadratic function f(x)=x^2+2x-15, find the following information: find the coordinates of the vertex as an ordered pair
Answers
f(x) = x² + 2x - 15
The x-coordinate of the vertex is computed as follows:
\(\begin{gathered} x_V=\frac{-b}{2a} \\ x_V=\frac{-2}{2(1)} \\ x_V=\frac{-2}{2} \\ x_V=-1 \end{gathered}\)To find the y-coordinate, you need to replace the x-coordinate into the formula, as follows:
\(\begin{gathered} y_V=x^2_v+2x_V-15 \\ y_V=(-1)^2_{}+2(-1)_{}-15 \\ y_V=1-2_{}-15 \\ y_V=-16 \end{gathered}\)Then, the vertex is at (-1, -16)
ASAP!!! Answer the following include all steps

Answers
Question 1:
(a) The equation representing Elaine's total parking cost is:
C = x * t
(b) So the cost of parking for a full 24 hours would be 24 times the cost per hour.
Question 2:
The given system of equations is inconsistent and has no solution.
(a) To represent Elaine's total parking cost, C, in dollars for t hours, we need to know the cost per hour. Let's assume the cost per hour is $x.
(b) If Elaine wants to park her car for a full 24 hours, we can substitute t = 24 into the equation from part (a):
C = x * 24
Question 2:
To solve the linear system:
-x - 6y = 5
x + y = 10
We can use the elimination method.
Multiply the second equation by -1 to create opposites of the x terms:
-x - 6y = 5
-x - y = -10
Add the two equations together to eliminate the x term:
(-x - 6y) + (-x - y) = 5 + (-10)
-2x - 7y = -5
Now we have a new equation:
-2x - 7y = -5
To check the answer, we can substitute the values of x and y back into the original equations:
From the second equation:
x + y = 10
Substituting y = 3 into the equation:
x + 3 = 10
x = 10 - 3
x = 7
Checking the first equation:
-x - 6y = 5
Substituting x = 7 and y = 3:
-(7) - 6(3) = 5
-7 - 18 = 5
-25 = 5
For more such questions on parking cost
https://brainly.com/question/18091509
#SPJ8
a jet airplane reaches 735./kmh on a certain flight. how long does it take to cover 186.m? set the math up. but don't do any of it. just leave your answer as a math expression. also, be sure your answer includes all the correct unit symbols.
Answers
Therefore, the math expression for the time taken is:
time = 186 m ÷ (735 km/h × 1000 m/km ÷ 3600 s/h) = 186 m ÷ 205 m/s = 0.9073 s
What is speed?Speed is a measure of how fast an object is moving relative to a reference point. It is defined as the distance traveled by an object in a given amount of time. The standard unit of measurement for speed is meters per second (m/s) in the metric system, but it can also be measured in miles per hour (mph), kilometers per hour (km/h), or other units depending on the context.
Given by the question.
We can use the formula:
distance = speed × time
To find the time taken to cover a distance of 186 m at a speed of 735 km/h, we first need to convert the speed to meters per second (m/s).
1 km = 1000 m
1 h = 3600 s
So,735 km/h = (735 × 1000) m/ (3600 s) = 205 m/s
Now, we can plug in the values into the formula:
186 m = 205 m/s × time
Solving for time, we get:
time = 186 m ÷ 205 m/s = 0.9073 s
To learn more about distance:
https://brainly.com/question/15172156
#SPJ1
Algebra 1 CR-8
Consider the function f(x) = x2 + 2x – 15.
What are the x-intercepts of the function?
Left-most x-intercept:
), o)
Right-most x-intercept: (/
0)
Answers
\(\mathrm{Domain\:of\:}\:x^2+2x-15\::\quad \begin{bmatrix}\mathrm{Solution:}\:&\:-\infty \:<x<\infty \\ \:\mathrm{Interval\:Notation:}&\:\left(-\infty \:,\:\infty \:\right)\end{bmatrix}\)
\(\mathrm{Range\:of\:}x^2+2x-15:\quad \begin{bmatrix}\mathrm{Solution:}\:&\:f\left(x\right)\ge \:-16\:\\ \:\mathrm{Interval\:Notation:}&\:[-16,\:\infty \:)\end{bmatrix}\)
\(\mathrm{Axis\:interception\:points\:of}\:x^2+2x-15:\quad \mathrm{X\:Intercepts}:\:\left(3,\:0\right),\:\left(-5,\:0\right),\:\mathrm{Y\:Intercepts}:\:\left(0,\:-15\right)\)
\(\mathrm{Vertex\:of}\:x^2+2x-15:\quad \mathrm{Minimum}\space\left(-1,\:-16\right)\)
Solve each equation for the variable. y/5 - 7 = - 1
Answers
In this case, we'll have to carry out several steps to find the solution.
Step 01:
Data
y/5 - 7 = - 1
y = ?
Step 02:
We must apply the algebraic rules.
y/5 - 7 = - 1
y/5 = - 1 + 7
y/5 = 6
y = 6 * 5
y = 30
The answer is:
y = 30
A floor tile is 2ft wide . Convert the width to inches
Answers
Answer: 24 inches
Step-by-step explanation:
First, remember that 1 ft is equal to 12 in
Then, if 1 ft = 12 in
1 = 12in/1ft
this means that we can write a constant:
C = 12in/1 in
and C = 1, then we can write the width 2ft as:
2ft = 2ft*C = 2ft*12in/1ft = 24in
A square garden has a length of (x+3) ft and a width of (x+2) ft. what is the perimeter and area of the garden?
Answers
Answer:
Perimeter:\(4x+10\) feet
Area:\(x^{2}+5x+6\) feet
Step-by-step explanation:
The perimeter is equal to 2*width +2*length. The width is x+2 and the length is x+3, therefore the perimeter is equal to 2x+4+2x+6 which equals 4x+10.
The area is equal to width*length
(x+3)(x+2)=\(x^{2}+2x+3x+6=x^{2}+5x+6\)
Determine the equation of FG?

Answers
The equation of line FG is given as follows:
y = -0.5x - 5.5.
How to obtain the equation of FG?The circle has a center of (1, -1), hence the equation is given as follows:
(x - 1)² + (y + 1)² = r².
Point (-1, -5) is on the circumference of the circle, hence the radius is obtained as follows:
(-1 - 1)² + (-5 + 1)² = r²
r² = 40.
Hence:
(x - 1)² + (y + 1)² = 40.
Applying implicit differentiation, the derivative is given as follows:
2(x - 1) + 2(y + 1)m = 0
2x - 2 +2m(y + 1) = 0
m = (x - 1)/(y + 1)
At x = -1 and y = -5, hence the slope is given as follows:
m = -2/4
m = -0.5.
Hence the equation is given as follows:
y + 5 = -0.5(x + 1).
y = -0.5x - 5.5.
More can be learned about the equation of a tangent line at https://brainly.com/question/7252502
#SPJ1
8. Rectangles AFGE and A B C D are similar; FG = 4 centimeters, EG = 6 centimeters
centimeters.
AC
15 cm
4 cm
G
6 cm
E
D
What is the length of BC in centimeters?

Answers
Answer:
14
Step-by-step explanation:
i got it right and you can tell that they are almost the same size.
what is quadratic formula?
Answers
Answer:
The quadratic formula allows us to solve any quadratic equation that's in the form ax^2 + bx + c = 0.
Step-by-step explanation:
Answer:
Step-by-step explanation:

Câu 1. Cho ánh xạ f : R
3 → R
3
, xác định bởi
f(x, y, z) = (4x − 5y + 5z, −5x − 6y, 3x + 5y − 2z).
a) Chứng minh rằng f là ánh xạ tuyến tính.
b) Tìm ma trận A của f đối với cơ sở
B = {e1 = (1, 0, 0); e2 = (2, 2, 0); e3 = (3, 3, 3)} trong R
3
Answers
what is your clear question? it lacks some details
Find the area of the shape
with the radius of 10
Answers
Answer: 314.16
Step-by-step explanation: To find the area of a circle you have to square the radius then multiply by pi. 10 squared is 100 then multiplied by pi is 314.16 (rounded to the nearest hundredth).
how to graph y=x+2 and get the correct answer
Answers
The graph of the linear equation y=x+2 is plotted.
How to draw the graph?In mathematics, a graph is a visual representation or diagram that shows facts or values in an ordered way. The relationships between two or more items are frequently represented by the points on a graph.
Identify the variablesDetermine the variable rangeDetermine the scale of the graphLabel all axis and name the graphFind the data points and plot them on graphDraw the graphThe given equation is:
y = x+2
Put value of 'x' and find 'y'
for x = 0, y = 2 : (0,2)
for x = 1, y = 3: (1,3)
for x = 2, y = 4 : (2, 4)
Thus, the graph of the linear equation y=x+2 is plotted.
know more about drawing the graph
https://brainly.com/question/12980786
#SPJ1

The width of a rectangle measures (k+3)(k+3) centimeters, and its length measures (k-9)(k−9) centimeters. Which expression represents the perimeter, in centimeters, of the rectangle?
Answers
Answer:
(k+3)(k+3) + (k-9)(k-9), or p = (k+3)^2 + (k-9)^2, or p = 4k^2 - 24k + 180
Step-by-step explanation:
A rectangle has four sides, two sides both have equal width, while the other two have equal length. The perimiter is the total sum of these sides. We can use the following equation to represent the perimiter using the width and length:
p = 2w + 2l
We know that the width equals (k+3)(k+3), so 2w would equal 2(k+3)(k+3). In the form of a quadratic equation, this would equal 2k^2+12k+18.
We also know that the length equals (k-9)(k-9), so 2l would equal 2(k-9)(k-9). As a quadratic equation, this would equal 2k^2-36k+162.
Plugging these values into our equation we get:
p = (k+3)(k+3) + (k-9)(k-9), or p = (k+3)^2 + (k-9)^2.
Or in the form of a quadratic equation:
p = 2k^2 + 12k + 18 + 2k^2 - 36k + 162
=
p = 4k^2 - 24k + 180
Hope this helps!
The perimeter of the rectangle can be calculated using the formula 2(length + width). Substituting the given expressions for length and width, we get 2[(k+3)(k+3)+(k-9)(k−9)]. This simplifies to the expression 4k^2-24k+180.
Explanation:The perimeter of a rectangle is calculated by adding the lengths of all its sides. With the width given as (k+3)(k+3) centimeters, and the length as (k-9)(k−9) centimeters, we can substitute these into the formula for the perimeter of a rectangle, which is 2(length + width).
Therefore, the expression representing the perimeter of the rectangle is 2[(k+3)(k+3)+(k-9)(k−9)]. This simplifies to 2[(k^2+6k+9)+(k^2-18k+81)], which further simplifies to 2[2k^2-12k+90], and ultimately simplifies to 4k^2-24k+180.
Learn more about perimeter here:https://brainly.com/question/31695951
#SPJ2
Clothing donations are collected to help a family in need. The function g(x) represents the number of items collected where x is the number of people who donated. Does a possible solution of (60,10) make sense for this function? Explain yojr answer
Answers
Answer:
No g(x) = x/6 for (60, 10) to be a possible solution
by this function 60 people would have to donate 1/6th of a garment each to achieve 10 full garments
Step-by-step explanation:
g(x) number of items
x number of people
the data point (60, 10) make sense as a possilbe solution NO
g(x) = number of items x = 60 g(x) = 10
g(60) = x/6 = 10
= 60/10
by this function 60 people would have to donate 1/6th of a garment each to achieve 10 full garments
(a) The number of terms in an arithmetic progression is 40 and the last is -54. Given that the sum of the 15 terms added to the sum of the first 30 terms is zero. Calculate (1) The first term and common difference, (ii) the sum of the progression.
Answers
(i) The first term (a) is 24 and the common difference (d) is -2.
(ii) The sum of the progression is 2520.
i) Finding the first term and common difference:
Given that the number of terms in the arithmetic progression is 40 and the last term is -54, we can use the formula for the nth term of an arithmetic progression to find the first term (a) and the common difference (d).
The nth term formula is: An = a + (n-1)d
Using the given information, we can substitute the values:
-54 = a + (40-1)d
-54 = a + 39d
We also know that the sum of the first 15 terms added to the sum of the first 30 terms is zero:
S15 + S30 = 0
The sum of the first n terms of an arithmetic progression can be calculated using the formula:
Sn = (n/2)(2a + (n-1)d)
Substituting the values for S15 and S30:
[(15/2)(2a + (15-1)d)] + [(30/2)(2a + (30-1)d)] = 0
Simplifying the equation:
15(2a + 14d) + 30(2a + 29d) = 0
30a + 210d + 60a + 870d = 0
90a + 1080d = 0
a + 12d = 0
a = -12d
Substituting this value into the equation -54 = a + 39d:
-54 = -12d + 39d
-54 = 27d
d = -2
Now we can find the value of a by substituting d = -2 into the equation a = -12d:
a = -12(-2)
a = 24
Therefore, the first term (a) is 24 and the common difference (d) is -2.
ii) Finding the sum of the progression:
The sum of the first n terms of an arithmetic progression can be calculated using the formula:
Sn = (n/2)(2a + (n-1)d)
Substituting the values:
S40 = (40/2)(2(24) + (40-1)(-2))
S40 = 20(48 - 39(-2))
S40 = 20(48 + 78)
S40 = 20(126)
S40 = 2520
Therefore, the sum of the arithmetic progression is 2520.
for such more question on common difference
https://brainly.com/question/25731911
#SPJ8
The actual volumes of quart-size jars of Hellmann's mayonnaise are uniformly distributed from 31.58 to 32.51 fluid ounces. Find the standard deviation in volumes of quart-size Hellmann's mayonnaise jars (in fluid ounces). NOTE: There are 32 fluid ounces in a quart.
Answers
Answer:
0.27
Step-by-step explanation:
The standard deviation of a uniform distribution is:
σ² = (b − a)² / 12
σ² = (32.51 − 31.58)² / 12
σ² = 0.0721
σ = 0.268
Rounded to the hundredths place, the standard deviation is 0.27.
To solve this question, we use concepts of the uniform probability distribution.
Using this, we get that the standard deviation in volumes of quart-size Hellmann's mayonnaise jars is of 0.2685 fluid ounces.
Uniform probability distribution:
An uniform distribution has two bounds, a and b.
The standard deviation is:
\(S = \sqrt{\frac{(b-a)^2}{12}}\)
The actual volumes of quart-size jars of Hellmann's mayonnaise are uniformly distributed from 31.58 to 32.51 fluid ounces.
This means that \(a = 31.58, b = 32.51\)
Find the standard deviation in volumes of quart-size Hellmann's mayonnaise jars (in fluid ounces).
\(S = \sqrt{\frac{(32.51 - 31.58)^2}{12}} = 0.2685\)
Thus, the standard deviation is of 0.2685 fluid ounces.
A similar example is given at https://brainly.com/question/15855314
Let u = - 3i + 2i v = 2i - 2j and w = - 4j Find the specified scalar or vector. 5u(3v - 4w)
Answers
If u = - 3i + 2i, v = 2i - 2j and w = - 4j, 5u(3v - 4w) is a scalar quantity with a value of 440.
To evaluate the expression 5u(3v - 4w), we need to first perform the scalar multiplication and then the vector subtraction. We can start by computing the scalar multiplication of 3v - 4w:
3v - 4w = 3(2i - 2j) - 4(-4j) = 6i + 14j
Next, we can perform the scalar multiplication of u and the vector 6i + 14j:
5u(3v - 4w) = 5(-3i + 2j)(6i + 14j)
Expanding the product, we get:
5(-18i² + 36ij + 42ij - 28j²)
Since i² = j² = -1, we can simplify this expression as:
5(18 + 70) = 440
Therefore, 5u(3v - 4w) is a scalar quantity with a value of 440.
The key concept used in this problem is the distributive property of scalar multiplication over vector addition and subtraction. This property allows us to simplify expressions that involve scalar multiplication and vector operations by distributing the scalar to each component of the vector.
To learn more about vectors click on,
https://brainly.com/question/9201864
#SPJ1
pls help me
For each set of three lengths, determine if they can be the side lengths of a triangle.
Lengths Can be side lengths of a triangle Cannot be side lengths of a triangle

Answers
Answer:
no
yes
no
no
Step-by-step explanation:
this should be true
a+b>c
a+c>b
b+c>a
This graph shows how fast a commuter train travels on its route in an urban area. What is the meaning of the point with an x-coordinate of 4
Answers
The meaning of the point with an x-coordinate of 2 is in 2 seconds, the commuter travels 120 feet.
What is an equation?An equation is an expression that shows the relationship between two or more numbers and variables.
Independent variables represent function inputs that do not depend on other values, while dependent variables represent function outputs that depends on other values.
From the graph, the x coordinate 2, have a y coordinate of 120. Hence:
The meaning of the point with an x-coordinate of 2 is in 2 seconds, the commuter travels 120 feet.
Find out more on equation at: https://brainly.com/question/2972832
#SPJ1

29. Mr. Ignado gave 4 orange erasers and 5 green erasers to each of the
20 students in his class. How many erasers did Mr. Ignado give to his
students?

Answers
Solve for x.
37°
8 cm
x = [?] cm
X
Round to the nearest hundredth.
X
![Solve for x.378 cmx = [?] cmXRound to the nearest hundredth.X](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/5r3s734YNpMZhrSKBRqrQYrII2vYUjgx.png)
Answers
The measure of side length x in the right triangle is approximately 6.03 cm.
What is the measure of side length x?The figure in the image is a right triangle having one of its interior angle at 90 degrees.
From the figure:
Angle θ = 37 degrees
Adjacent to angle θ = 8 cm
Opposite to angle θ = x
To solve for the missing side length x, we use the trigonometric ratio.
Note that: tangent = opposite / adjacent
Hence:
tan( θ ) = opposite / adjacent
Plug in the given values and solve for x:
tan( 37 ) = x / 8
x = tan( 37 ) × 8
x = 6.03 cm
Therefore, the value of x is 6.03 cm.
Learn more about trigonometric ratio here: brainly.com/question/28016662
#SPJ1
I just need help with the range domain is [-2,3)

Answers
Answer:
We don't need to worry about the displaystyle- {3} −3 anyway, because we dcided in the first step that displaystyle {x}ge- {2} x ≥ −2. So the domain for this case is displaystyle {x}ge- {2}, {x}ne {3} x≥ −2,x≠ 3, which we can write as displaystyle {left [- {2}, {3}right)}cup {left ({3},inftyright)} [−2,3)∪(3,∞).
Step-by-step explanation: