When a ribbon is cut into 3 equal pieces,each piece is _______ m long (correct to 2 decimal places).
Answers
Answer:
How long was the ribbon before it was cut?
Step-by-step explanation:
Related Questions
If -4/3y=-3/4, then y =?
Answers
Step-by-step explanation:
y=-3/4 ÷ -4/3
y=+9/16
Answer:
So we have this equation:
\(\frac{-4}{3y}=\frac{-3}{4}\)
We can multiply both sides by 4 and 3y:
\(\frac{-4*4*3y}{3y}=\frac{-3*4*3y}{4}\)
\(-4*4=-3*3y\)
\(-16 = -9y\)
Now we divide both sides by 9:
\(\frac{-16}{-9}=y\)
And we can remove the minus signs:
\(\frac{16}{9}=y\)
If you mean \(\frac{-4}{3}y=\frac{-3}{4}\):
\(-4y*4=-3*3\)
\(-16y = -9\)
\(y=\frac{9}{16}\)
write an equation for a line parallel to y=-2x-1 that passes through (2,-7)
Answers
Answer:
The equation is;
y = -2x - 3
Step-by-step explanation:
If two lines are parallel, then they have an equal value of slope
Mathematically we can generally have the equation of a line written as;
y = mx + c
where m
is slope and c is the y-intercept
In the case of the equation given, the slope of the line is -2
So technically, we want to get the equation of a line that has a slope of -2 and it passes through (2,-7)
The point-slope form can be written as;
y-y1 = m(x-x1)
So the equation we want to get is;
y-(-7) = -2(x-2)
y + 7 = -2x + 4
y = -2x + 4 - 7
y = -2x - 3
(2x–y)²–(y+2)²-----------
Answers
Answer:
4x² -4xy -4y -4
Step-by-step explanation:
\(\boxed{ {a}^{2} - {b}^{2} = (a + b)(a - b)}\)
In this case, a= 2x -y and b= y +2.
(2x -y)² -(y +2)²
= (2x -y +y +2)[2x -y -(y +2)]
= (2x +2)(2x -y -y -2)
= (2x +2)(2x -2y -2)
= 2x(2x) +2x(-2y) +2x(-2) +2(2x) +2(-2y) +2(-2) (expand)
= 4x² -4xy -4x +4x -4y -4
= 4x² -4xy -4y -4
Alternatively, start by expanding the brackets.
\(\boxed{(a - b)^{2} = {a}^{2} - 2ab \: + {b}^{2} }\)
\(\boxed{(a + b)^{2} = {a}^{2} + 2ab \: + {b}^{2} }\)
(2x -y)² -(y +2)²
= 4x² -4xy +y² -(y² +4y +4)
= 4x² -4xy +y² -y² -4y -4 (expand)
= 4x² -4xy -4y -4 (simplify)
the following question

Answers
Answer:
angle ODC=30°
Step-by-step explanation:
Parallel to the line now draw another line PQ


A golf store pays its wholesaler $40 for a certain club. and then sells it to a golfer for $75. What is the markup rate?
Answers
Answer:
87.5% increase
Step-by-step explanation:
75 - 40 = 35
Find what percentage 35 is of 40, and you can do so by dividing.
35 ÷ 40 = 0.875
0.875 = 87.5%
I need help with this question
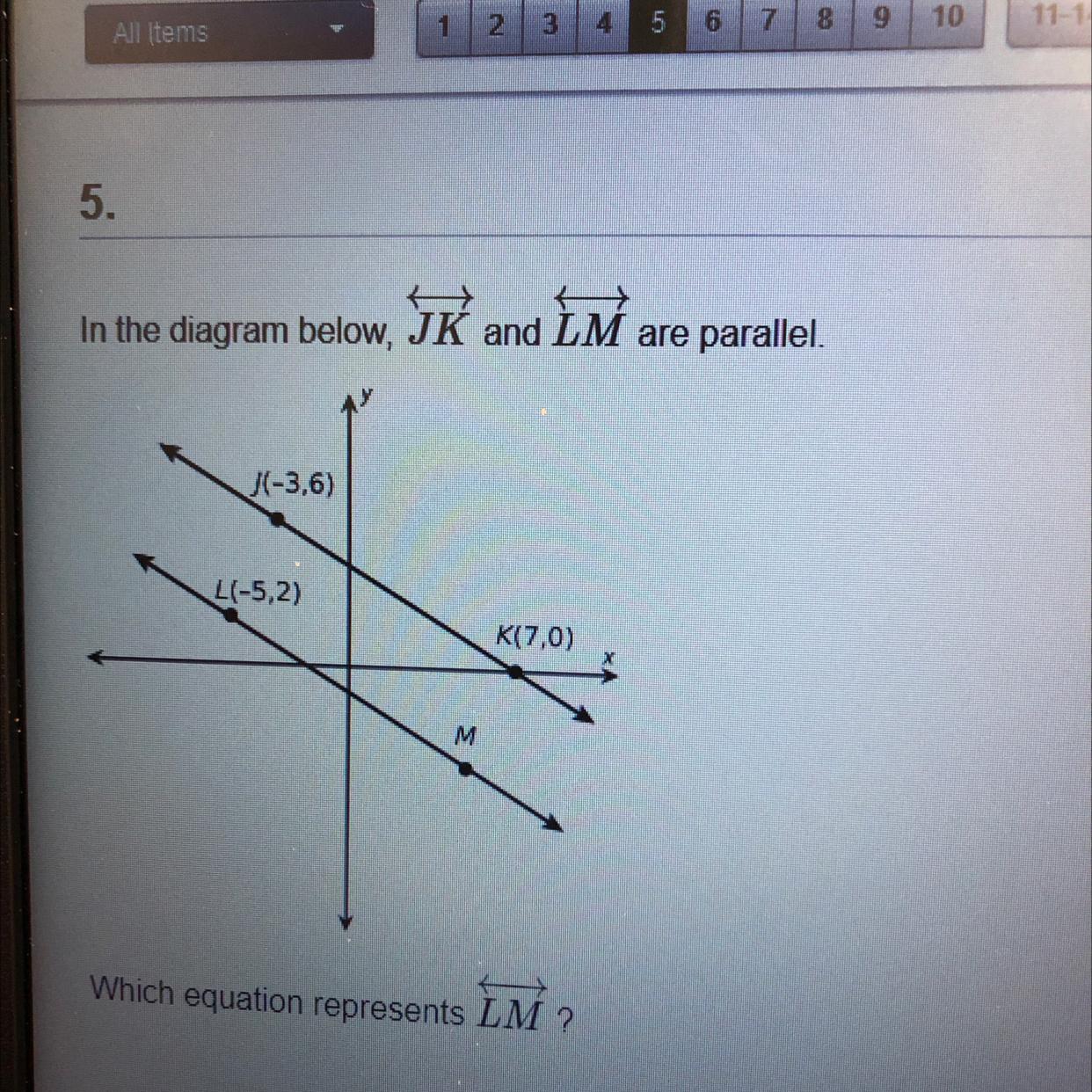
Answers
Answer:
-5,2
Step-by-step explanation:
it literally represents LM and Shows it on the graph
What value of z should we use when making a 93% confidence interval for p?.
Answers
The crucial value (z) relies on the desired level of confidence and is predicated on a normal distribution when creating a confidence interval for a proportion (p) with a confidence level of 93%.
A 93% confidence level in this instance translates to an alpha level of 0.07 (1 - 0.93 = 0.07) that is split evenly between the two tails. In the usual normal distribution table, we search for the value that falls within the range of 0.07 to find the proper z-value. A 93% confidence level corresponds to a z-value of roughly 1.81. The confidence interval for the proportion p may be calculated using this number and provides a range where the genuine proportion is like to fall.
learn more about proportion here :
https://brainly.com/question/31548894
#SPJ11
How is solving 2x c= d similar to solving 2x 1 = 9 for how are they different? how can you use 2x c= d to solve 2x 1 = 9? free anser
Answers
The value of x is x = 9/4. The equation 2xc = d as follows: 2xc = d2x * 1/2 = 9/22x = 9/2 * 2x = 9/4
The equation 2xc = d and 2x + 1 = 9 are similar in that they are both linear equations and involve the variable x.
However, they are different in that they have different constants and coefficients.
How to use 2xc = d to solve 2x + 1 = 9? To use 2xc = d to solve 2x + 1 = 9, you first need to rewrite 2x + 1 = 9 in the form 2xc = d.
To do this, you need to isolate x on one side of the equation. 2x + 1 = 9
Subtract 1 from both sides2x = 8. Divide both sides by 2x = 4Now, we can write 2x + 1 = 9 as 2x * 1/2 = 9/2.
Therefore, we can see that this equation is similar to 2xc = d, where c = 1/2 and d = 9/2.
We can use this relationship to solve for x in the equation 2xc = d as follows: 2xc = d2x * 1/2 = 9/22x = 9/2 * 2x = 9/4 Therefore, x = 9/4.
To know more about value visit:
brainly.com/question/20532123
#SPJ11
This is a easy question, but what is the easiest way you could solve for slope?
:) ty
Answers
Terms in this set (8)
Slope. y2 - y1 / x2 - x1 = slope.
Slope Intercept form. y = mx + b.
Point slope form. y - y1 = m ( x - x1)
Standard Form. Ax + By = C.
x - axis. The horizontal line on a graph.
y - axis. The vertical line on a graph.
X - intercept. The point on a line that intercepts on the x axis.
Y - intercept.
In a study of cell phone usage and brain hemispheric dominance, an internet survey was e-mailed to subjects randomly selected from an online group involved with ears. There were surveys returned. Use a 0. 01 significance level to test the claim that the return rate is less than 20%. Use the p-value method and use the normal distribution as an approximation to the binomial distribution.
Answers
The statistics z is -1.878 and the p value is 0.0302
Given,
Number of random sample selected, n = 6967
Number of surveys returned, x = 1331
Estimated proportion of return rate;
p = 1331/6967 = 0.192
Significance level, ∝ = 0.01
z would represent the statistic
We investigate the assertion that the return rate is less than 20%, and the following hypotheses are tested:
Null hypothesis, p₀ ≥ 0.2
Alternative hypothesis, p₀ < 0.2
The statistics, z = (p - p₀) / √(p₀(1 - p₀)/n)
That is,
z = (0.191 - 0.2) / √(0.2(1 - 0.2)/6967) = -1.878
Using the alternative hypothesis and the following probability, we can now get the p value:
p value = p(z < - 1.878) = 0.0302
We fail to reject the null hypothesis when the p value exceeds the significance level of 0.01 and there is insufficient evidence to support the conclusion that the return rate is less than 20% at 1% of significance.
Learn more about statistics here;
https://brainly.com/question/16528376
#SPJ4
What is the value of the polynomial 4x² 7x 5 when x 3?
Answers
When X=3 a polynomial has a value of 61 and when X=3 a value of 143.
Given that,
Let p(x)=3x²−4x²+7x−5 is our polynomial.
Polynomials are algebraic expressions made up of coefficients and variables. Occasionally, variables are referred to as indeterminates. For polynomial expressions, addition, subtraction, multiplication, and positive integer exponents are all possible; however, division by variable is not. x2+x-12 is an illustration of a single-variable polynomial. Three terms are involved in this example: x2, x, and -12.
Substitute x=3 in above expression,
∴p(3)=3(3) 3−4(3) 2 +7(3)−5
=3(27)−4(9)+21−5
=81−36+21−5
=61
Now,
p(−3)=3(−3)
3 −4(−3) 2 +7(−3)−5
=3(−27)−4(9)−21−5
=−81−36−21−5
=−143
So, value of polynomial when X=3 is 61 and when x=−3 is −143
To learn more about the polynomial click here :
brainly.com/question/11536910
#SPJ4
need help with this refer to picture

Answers
Answer:
Step-by-step explanation:

the table below gives beverage preferences for random samples of teens and adults. beverage teens adults total coffee 50 200 250 tea 100 150 250 soft drink 200 200 400 other 50 50 100 400 600 1,000 we are asked to test for independence between age (i.e., adult and teen) and drink preferences. refer to exhibit 12-5. what can be concluded from this test? a. there is enough evidence to conclude that age and drink preference is dependent. b. there is not enough evidence to conclude that age and drink preference is dependent. c. the test is inconclusive. d. the test should be done again to be certain of the results.
Answers
The correct answer is (a) there is enough evidence to conclude that age and drink preference is dependent.
How to explain the informationUsing the formula for the chi-square test of independence, we can calculate the test statistic as:
X² = Σ (O-E)^2 / E
Performing this calculation on the given data, we get:
X² = (50-62.5)²/62.5 + (100-87.5)²/87.5 + (200-250)²/250 + (200-200)²/200 + (50-50)²/50 + (200-150)²/150 + (50-37.5)²/37.5 + (150-162.5)²/162.5 + (200-250)²/250 + (50-50)²/50 = 34
Using a chi-square distribution table with (2-1)*(4-1)=3 degrees of freedom and a significance level of 0.05, the critical value is 7.815.
Since the calculated test statistic of 34 is greater than the critical value of 7.815, we can reject the null hypothesis of independence and conclude that there is enough evidence to support the alternative hypothesis that age and drink preference are dependent.
Learn more about evidence on
https://brainly.com/question/1256677
#SPJ1
the first three term of the sequence -8,x,y,72 form an arithmetic sequence, while the second, third ,and fourth terms form a geometric sequence. determine x and y
Answers
To solve for x and y in this problem, we need to use the formulas for arithmetic and geometric sequences.
For the arithmetic sequence, we know that the difference between each term is the same. Let's call this difference "d". So we have:
-8 + d = x
x + d = y
y + d = 72
For the geometric sequence, we know that the ratio between each term is the same. Let's call this ratio "r". So we have:
x * r = y
y * r = 72
Now we can use these equations to solve for x and y.
First, we'll use the arithmetic sequence equations to find the value of "d". We can subtract the first equation from the second equation to get:
d = y - x
We can then substitute this into the third equation to get:
y + (y - x) = 72
Simplifying this, we get:
2y - x = 72
Now we can use the geometric sequence equations to find the value of "r". We can divide the second equation by the first equation to get:
r = y/x
We can then substitute this into the first equation to get:
x * (y/x) = y
Simplifying this, we get:
y = x^2
Now we have two equations for "y", so we can substitute one into the other to get an equation in terms of "x" only:
2x^2 - x = 72
Solving this quadratic equation, we get:
x = -8 or x = 9
We can then substitute each of these values back into the equation y = x^2 to get:
y = 64 or y = 81
So the solutions are:
x = -8, y = 64
x = 9, y = 81
Therefore, the first three terms of the sequence are -8, -8+17=9, 9+17=26 and the second, third, and fourth terms are 9, 26, 72.
In an arithmetic sequence, the difference between consecutive terms is constant. In a geometric sequence, the ratio between consecutive terms is constant.
Given the arithmetic sequence: -8, x, y, the difference between consecutive terms is constant, so we can say that x - (-8) = y - x. Simplifying, we get x + 8 = y - x, and then 2x = y - 8 (Equation 1).
Now, considering the geometric sequence: x, y, 72, the ratio between consecutive terms is constant. Therefore, y/x = 72/y. By cross-multiplying, we obtain y^2 = 72x (Equation 2).
To determine x and y, we can solve this system of equations. Using Equation 1, y = 2x + 8. Substitute this expression for y in Equation 2:
(2x + 8)^2 = 72x
4x^2 + 32x + 64 = 72x
4x^2 - 40x + 64 = 0
x^2 - 10x + 16 = 0
(x - 8)(x - 2) = 0
From this quadratic equation, we have two possible values for x: x = 8 or x = 2.
If x = 8, then y = 2x + 8 = 24. This would result in the geometric sequence 8, 24, 72, which has a constant ratio of 3.
If x = 2, then y = 2x + 8 = 12. This would result in the geometric sequence 2, 12, 72, which has a constant ratio of 6.
Both solutions are valid, so we have two possible sets of values for x and y: x = 8, y = 24 or x = 2, y = 12.
Learn more about geometric at : brainly.com/question/11266123
#SPJ11
The solutions for x and y are: 1. x = 2, y = 12 and
2. x = 8, y = 24
How did we get the values?To determine the values of x and y in the sequence -8, x, y, 72, analyze the information given.
First, consider the arithmetic sequence formed by the first three terms: -8, x, y. In an arithmetic sequence, the common difference between consecutive terms is constant.
Therefore, set up the following equation:
x - (-8) = y - x
Simplifying the equation, we have:
x + 8 = y - x
2x + 8 = y
Next, given that the second, third, and fourth terms form a geometric sequence: x, y, 72. In a geometric sequence, each term is obtained by multiplying the previous term by a constant ratio.
Express this relationship using the following equation:
y / x = 72 / y
Cross-multiplying, we get:
y² = 72x
Now, we have two equations:
2x + 8 = y (Equation 1)
y² = 72x (Equation 2)
To solve for x and y, we'll substitute Equation 1 into Equation 2:
(2x + 8)² = 72x
Expanding and simplifying:
4x² + 32x + 64 = 72x
Rearranging the terms:
4x² + 32x - 72x + 64 = 0
4x² - 40x + 64 = 0
Dividing the entire equation by 4:
x² - 10x + 16 = 0
Factoring the quadratic equation, we have:
(x - 2)(x - 8) = 0
Setting each factor equal to zero and solving for x, we get:
x - 2 = 0 -> x = 2
x - 8 = 0 -> x = 8
So, x can be either 2 or 8.
If we substitute these values back into Equation 1, we can find the corresponding values of y:
For x = 2:
2(2) + 8 = y
4 + 8 = y
12 = y
For x = 8:
2(8) + 8 = y
16 + 8 = y
24 = y
Therefore, the possible solutions for x and y are:
1. x = 2, y = 12
2. x = 8, y = 24
learn more about geometric sequence: https://brainly.com/question/1509142
#SPJ4
Will the answer to this expression be POSITIVE or NEGATIVE?
12 - 22
Answers
Answer:
the answer is -10
Step-by-step explanation:
the steps are in the picture

Answer:
The answer to this expression would be negative.
Step-by-step explanation:
-10
0
1
2
3
4
5.
6
I don’t know what I’m doing
Answers
Answer:
me neither (TT)(TT)(TT)(TT)(TT)(TT)(TT)(TT)(TT)(TT)(TT)

if 26 children were to be born in a hospital on a given day, how many combinations of 6 boys and 20 girls would exist? 230,230 4 x 10^26 500,000 15 Z
Answers
The number of combinations of 6 boys and 20 girls that can exist among 26 children born in a hospital on a given day is 230,230.
]To calculate the number of combinations, we can use the concept of binomial coefficients. The formula for calculating the number of combinations is C(n, k) = n! / (k!(n-k)!), where n is the total number of objects and k is the number of objects we want to select.
In this case, we have 26 children in total, and we want to select 6 boys and 20 girls. Plugging these values into the formula, we get C(26, 6) = 26! / (6!(26-6)!) = 230,230. Therefore, there are 230,230 different combinations of 6 boys and 20 girls that can exist among the 26 children born in the hospital on that given day.
Learn more about combinations here : brainly.com/question/28065038
#SPJ11
need help fast will give BRAINLIEST

Answers
Answer:
c. x <_ -2 or x >_ 4
Step-by-step explanation:
On the number line, the line goes infinity both sides, but stops between x= -2 and x=4
PLEASE HELP ME WITH GEOMETRY!!! Please

Answers
Answer:
100
Step-by-step explanation:
What you need to do is multiply all of the numbers together so the three sides equal 12 so you need to do 12x3 which equals to 36 and 8x8 is 64 and then add 64 and 36 which gives you 100
Solution :
The given figure consists of two shapes that are a triangle and a square . To find the total area of the figure we will first find the area of the triangle then that of the square and add them .
Let's work on this ,
Area of triangle \(\sf\implies\::\dfrac{1}{2}\:\times\:base\:\times\:height\)In the given figure the base of the triangle is 12 inches and it's height is 8 inches .
\(\sf\implies\::\dfrac{1}{2}\:\times\:12\:\times\:8\)6 × 8 48 inches²Now lets find the area of the square ,
Area of square = Side × Side12 × 12144 inches²Total area of the figure
Area of triangle + Area of square 48 + 144192 inches²If f(x, y) = xy, find the gradient vector ∇f(4, 7) and use it to find the tangent line to the level curve f(x, y) = 28 at the point (4, 7). a) gradient vector b) tangent line equation c)Sketch the level curve, the tangent line, and the gradient vector.
Answers
To find the gradient vector ∇f(4, 7), we need to compute the partial derivatives of f(x, y) = xy with respect to x and y.
Given:
f(x, y) = xy
Partial derivative with respect to x (keeping y constant):
∂f/∂x = y
Partial derivative with respect to y (keeping x constant):
∂f/∂y = x
So, the gradient vector ∇f(4, 7) is (∂f/∂x, ∂f/∂y) evaluated at (4, 7):
∇f(4, 7) = (7, 4)
The equation of the tangent line to the level curve f(x, y) = 28 at the point (4, 7) can be written as:
z - f(4, 7) = ∇f(4, 7) · (x - 4, y - 7)
Substituting the values:
z - 28 = (7, 4) · (x - 4, y - 7)
Expanding the dot product:
z - 28 = 7(x - 4) + 4(y - 7)
z - 28 = 7x - 28 + 4y - 28
z = 7x + 4y - 56
Therefore, the equation of the tangent line to the level curve f(x, y) = 28 at the point (4, 7) is z = 7x + 4y - 56.
To sketch the level curve, the tangent line, and the gradient vector, you can plot the points on a graph with x and y coordinates and represent the tangent line as a straight line passing through the point (4, 7) with a slope of 7/4. The gradient vector (7, 4) can be represented as an arrow starting from the point (4, 7) in the direction of the vector.
learn more about vector here
https://brainly.com/question/24256726
#SPJ11
Suppose point D is in the interior of ∠ABC
, m∠ABC=12x−110
, m∠ABD=3x+40
, and m∠DBC=2x−10
. W
Answers
Answer:
\(ABC = 130\)
Step-by-step explanation:
Given
\(ABC=12x - 110\)
\(ABD=3x+40\)
\(DBC=2x - 10\)
Required
Determine the measure of ABC --- Missing part of the question
First, we need to determine the value of x
Since, D is an interior of ABC, then
\(ABC = ABD + DBC\)
\(12x - 110 = 3x + 40 + 2x - 10\)
Collect Like Terms
\(12x - 3x - 2x = 110 + 40 - 10\)
\(7x = 140\)
Solve for x
\(x = 140/7\)
\(x = 20\)
Substitute 20 for x in \(ABC=12x - 110\)
\(ABC = 12 * 20 - 110\)
\(ABC = 240 - 110\)
\(ABC = 130\)
On Monday, ALL the Grade 7 students either bought their lunch at the canteen or brought their lunch from home. Given that 20% of the students bought their lunch at the canteen and 116 students brought lunch from home, how many students are in Grade 7?
Answers
Answer:
145
.8x = 116 (80% of class is 116)
x=145
Step-by-step explanation:
Find the area of the parallelogram with adjacent sides u (9,8, 0) and v = (0, 8, 1) Consider vectors v, w, and w. u = (-3, 4, -1), v = (0, 2, -2), and w = (3, 1, 1) (a) Find the triple scalar product u. (v * w). (b) Find the volume of the parallelepiped (in units) with the adjacent edges u, v, and w. units 3 Find the distance from point P(2, 8, -7) to the plane of equation 4x - y + 3z - 9 = 0.
Answers
Answer:
The area of a parallelogram with adjacent sides u and v is given by the magnitude of the cross product of u and v:
A = |u x v|
We can find the cross product as follows:
u x v = (8)(-1) - (0)(-2), -(9)(-2) - (-3)(1), (9)(2) - (-3)(8) = (-8, -15, 42)
So the area of the parallelogram is:
A = |(-8, -15, 42)| = √(8^2 + 15^2 + 42^2) ≈ 46.09 square units
(a) The triple scalar product of three vectors u, v, and w is given by:
u . (v x w)
We can find the cross product v x w as follows:
v x w = (2)(1) - (-2)(1), (-2)(3) - (0)(1), (0)(1) - (2)(1) = (4, -6, -2)
So the triple scalar product is:
u . (v x w) = (-3)(4) - (4)(-6) - (-1)(-2) = -12 + 24 - 2 = 10
(b) The volume of a parallelepiped with adjacent edges u, v, and w is given by the scalar triple product of u, v, and w:
V = |u . (v x w)|
We already found u . (v x w) in part (a), so we just need to take the absolute value:
V = |10| = 10 cubic units
To find the distance from point P to the plane, we can use the formula:
d = |ax + by + cz + d| / sqrt(a^2 + b^2 + c^2)
where the equation of the plane is given by ax + by + cz + d = 0. In this case, we have:
a = 4, b = -1, c = 3, and d = -9
So the equation of the plane is 4x - y + 3z - 9 = 0. To find the distance from point P(2, 8, -7), we plug in these values:
d = |(4)(2) + (-1)(8) + (3)(-7) - 9| / sqrt(4^2 + (-1)^2 + 3^2) ≈ 5.61 units
Therefore, the distance from point P to the plane is approximately 5.61 units.
rate5* po and give thanks for more po! your welcome!
The graph of a linear of y in terms of passes through the points located at (- 3, 4) and (2, - 6) in the coordinate plane Which value represer the rate of change of y with respect to this function Select one answer
Answers
the rate of change of y with a linear function is the slope, so we just need to calculate
\(m=\frac{y_2-y_1}{x_2-x_1}\)with the points (x1,y1) and (x2,y2)
now replaced with the points (- 3, 4) and (2, - 6)
\(\frac{(-6)-4}{2-(-3)}=\frac{-10}{5}=-2\)So the answer is: -2
Jason is scuba diving at a constant rate toward the ocean floor. The equation
y= -2.5x – 5 can be used to represent this situation, where y is the depth of Jason in meters
below sea level and x is the number of seconds Jason has been swimming.
Which statement best describes the depth of Jason, given this equation?
Jason started scuba diving 2.5 meters below sea level and is ascending at a rate of 2.5 meters per
second.
Jason started scuba diving 5 meters below sea level and is ascending at a rate of 2.5
meters per second.
Jason started scuba diving 2.5 meters below sea level and is descending at a rate of 2.5
meters per second.
Jason started scuba diving 5 meters below sea level and is descending at a rate of 2.5
meters per second.
Answers
Answer:
Jason started scuba diving 5 meters below sea level and is descending at a rate of 2.5 meters per second.
Step-by-step explanation:
Jason is scuba diving at a constant rate toward the ocean floor.
Equation: \(y= -2.5x- 5\)
x = The number of seconds Jason has been swimming.
y=The depth of Jason in meters below sea level
General equation : y=mx+c
m = Slope = rate of change per unit
On comparing m = -2.5
Negative signs represents the descending .
So, rate of descending per second = 2.5 m/sec
-5 denotes the initial position below sea level
So, Option D is true
So, Jason started scuba diving 5 meters below sea level and is descending at a rate of 2.5 meters per second.
The perimeters of the two rectangles at right are equal. Write and solve an equation to find the value of x and the common perimeter. (desperate need of help)


Answers
Answer:
write the expression for the perimeter of the 1st rectangle 6x
write the expression for the perimeter of the 2nd rectangle 4x + 30
write the equation 6x = 4x + 30
x= 15
perimeter = 90
Step-by-step explanation:
The perimeter is adding up all the sides of the rectangle.
So for the first one, we know two of the sides: x and 2x. The opposite sides have the same values. So the other two sides are x and 2x.
Therefore, the perimeter is
2x + x + 2x + x
or
6x
Similarly with the second rectangles:
(x+12) + (x+3) + (x+12) + (x+3)
Combine like terms
x + x + x + x + 12 + 3 + 12 + 3
4x + 30
Set these two equal to each other because the two perimeters are equal
6x = 4x + 30
Subtract 4x on both sides
2x = 30
Divide by 2 on both sides
x = 15
Check:
6(15) = 4(15) + 30
90 = 60 + 30
90 = 90
The common perimeter is
6*15 = 90 units
Is it correct in adding subtracting?? Answer is in the picture please give me answer soon

Answers
Answer:
8/24 is correct. However, I would simplify 8/24 down to 1/3, since most teachers want you to do that.
The graph shows the dilation of ΔABC with the origin as its center. Which rule describes this transformation? A) (x, y) → (2x, 2y) B) (x, y) → (0.5x, 0.5y) C) (x, y) → (x + 2, y +2) D) (x, y) → (x - 2, y - 2)
Answer the right question then you get brainliest

Answers
The answer is A
Step-by-step explanation:
You multiply when you scale up
Four years ago Jim was p years. Four years after his age will be ________ years
please answer fasttttttttttt
very urgent
Answers
Answer:
p+4
please mark brainliest ♡
The output (from R) of principal component analysis are provided below: > eigen(cov_matrix) eigen() decomposition Svalues [1] 6.931073601.785144340.389649920.229528920.01415498 > summary (ゆC) Importance of comporents: standard deviation pranortion of variance 2.53692670.7413268 Comp. I Comp.2 0.1909337 comp.3 0.04167579 comp.4 0.02454972 Cumuliative proportion 0.74132680.93226050.973936300.99848603 etandand daviztion 0.114646905 proportion of variance 0.001513975 cunulative proportion 1.000000000
How many Principal component is enough to summarize the data here? Provide all possible explanation with evidence (given in this output).
Answers
Based on the eigenvalues and the summary of importance, we find that two principal components are enough to summarize the data. These components capture a substantial proportion of the variance and adequately represent the underlying patterns in the dataset.
In the given output, we have the eigenvalues: 6.93107360, 1.78514434, 0.38964992, 0.22952892, and 0.01415498. The eigenvalues represent the amount of variance explained by each principal component. The larger the eigenvalue, the more significant the component.
Additionally, the summary of importance provides the standard deviation, proportion of variance, and cumulative proportion for each principal component.
From the summary, we can see that the first component (Comp. I) has a standard deviation of 2.5369267 and accounts for 74.13% of the variance. The second component (Comp. 2) has a standard deviation of 0.7413268 and explains an additional 19.09% of the variance. The cumulative proportion shows that the first two components together explain 93.23% of the variance.
Based on this information, we can conclude that the first two principal components are sufficient to summarize the data. They capture a significant amount of the total variance (93.23%) and provide a good representation of the underlying patterns in the dataset.
Including additional components would explain a diminishing amount of variance. Therefore, using the first two principal components is a reasonable choice for summarizing the data effectively.
Visit here to learn more about standard deviation:
brainly.com/question/475676
#SPJ11