what's the double of 60
Answers
The double of 60 is just two times 60, so:
Answer:120
Step-by-step explanation: Just do 60x2=120
Related Questions
Which of the answer choices has matrix multiplication defined?

Answers
Answer:
b. BC
Step-by-step explanation:
The first thing is to calculate the dimensions of each matrix, that is, the number of rows x number of columns:
dimensions of A: 2x2
B dimensions: 2x3
C dimensions: 3x3
D dimensions: 1x3
We have that a matrix multiplication is defined, the internal numbers of its dimensions must be the same: we analyze each option:
BA: (2x3) * (2x2): the internal numbers do not match (a 3 for B and a 2 for A), so the multiplication of the matrix is not defined
BC: (2x3) * (3x3): the internal numbers are both 3, so the matrix multiplication is defined
CB: (3x3 ) * (2x3): the internal numbers do not match (a 3 for C and a 2 for B), so the multiplication of the matrix is not defined
CD: (3x3) * (1x3): the internal numbers do not match (a 3 for C and a 1 for D) so the multiplication of the matrix is not defined
Therefore the answer is b. BC
what subtracting a countably infinite set from a uncountably infinite set results in an uncountably infinite set
Answers
A is finite, then X - A is clearly uncountable (since it has the same cardinality as X). If A is countable but not infinite, then X - A is still uncountable (since it has the same cardinality as X). Thus, the only interesting case is when A is countably infinite.
Let X be an uncountable set and A be a countably infinite subset of X. We need to show that X - A is uncountable. By contradiction, assume that X - A is countable. Since A is countably infinite, we can list its elements in a sequence as {a1, a2, a3, ...}. Now, consider the following sequence of sets:S1 = X - {a1}S2 = S1 - {a2}S3 = S2 - {a3}...Sn = Sn-1 - {an}...Observe that each Si is obtained by removing a finite set from X, and hence Si is uncountable. Moreover, Si is a subset of Si-1 for each i, so we have an infinite descending chain of uncountable sets. This contradicts the fact that X is uncountable. Therefore, X - A must be uncountable.Note that this argument works for any uncountable set X, regardless of its cardinality. We only need to assume that A is countably infinite. If A is finite, then X - A is clearly uncountable (since it has the same cardinality as X). If A is countable but not infinite, then X - A is still uncountable (since it has the same cardinality as X). Thus, the only interesting case is when A is countably infinite.
Learn more about countable here:
https://brainly.com/question/13424103
#SPJ11
The sum of two numbers is 44. The second number is 4 less than three times the first number. Let x represent the first number and let y represent the second number. If the table will be used to guess and check, what should the equation be at the top of the last column?
Numbers
x
y
x + y = 44
?
y = 3 minus 4 x
y = 4 x minus 3
y = 4 minus 3 x
y = 3 x minus 4
Answers
Answer:
\( y = 4minus3 \times \)
\(let x = 44 \\ \\ lety = 4 \\ \\ x + y = 44 \\ \\ 12 \times 4 - 4 = 44\)
Answer:
y = 3 x minus 4
Step-by-step explanation:
hope this helped
Which value for x would make the statement true? -8x = -32
Answers
Nvdhnchfnfucndhcnfhchdnc
Step-by-step explanation:
Hey there!
Given;
-8x= -32
~ Divide both sides by"-8".
(-8x)/-8 = (-32)/-(8)
Or, X= 4.
Therefore, the value of x must be 4.
Check:
-8*4 = -32
-32 = -32 (True)
Hope it helps...
Determine the constant of variation for the direct variation given. Type a numerical answer in the space provided.
Answers
Answer:
B. 4
Step-by-step explanation:
Determine the constant of variation for the direct variation given.
(0, 0), (3, 12), (9, 36)
A. 3
B. 4
C.12
Direct variation is given by:
y = kx
Where,
k = constant of variation
(3, 12)
x = 3; y = 12
y = kx
12 = k*3
12 = 3k
k = 12 / 3
k = 4
(9, 36)
x = 9; y = 36
y = kx
36 = k * 9
36 = 9k
k = 36 / 9
= 4
k = 4
Constant of the variation = 4
1. Use Horner's algorithm to find p(4), where p(z) = 3z^2 – 7z^4 – 5z^3+z^2 -- 8z +2. 2. (Continuation) For the polynomial of preceding problem, find its expansion in a Taylor series about the point z0 = 4. 3. (Continuation) For the polynomial of Problem 3.5.1 (above), start Newton's method at the point z0 = 4. What is z1?
Answers
Evaluating p(4) using Horner's algorithm:
1. To use Horner's algorithm, we write the polynomial in nested form as follows:
p(z) = ((3z - 7)z - 5)z^2 + (z - 8)z + 2
Now, we can evaluate p(4) by starting from the inside and working our way out:
p(4) = ((3(4) - 7)4 - 5)4^2 + (4 - 8)4 + 2
= (5)4^2 - 4 + 2
= 78
Therefore, p(4) = 78.
2. Finding the Taylor series expansion of p(z) about z0 = 4:
To find the Taylor series expansion of p(z) about z0 = 4, we need to compute the derivatives of p(z) at z0 = 4. First, we compute p'(z) = 6z^2 - 28z^3 - 10z^2 + 2z - 8, then p''(z) = 12z - 84z^2 - 20z + 2, p'''(z) = 12 - 168z - 20, and so on.
Using these derivatives, we can write the Taylor series expansion of p(z) about z0 = 4 as follows:
p(z) = p(4) + p'(4)(z - 4) + p''(4)(z - 4)^2/2! + p'''(4)(z - 4)^3/3! + ...
Substituting in the values we computed, we get:
p(z) = 78 + 10(z - 4) - 41(z - 4)^2/2! - 14(z - 4)^3/3! + ...
Therefore, the Taylor series expansion of p(z) about z0 = 4 is:
p(z) = 78 + 10(z - 4) - 20.5(z - 4)^2 - 2.333(z - 4)^3 + ...
3. Using Newton's method to find a root of p(z):
To use Newton's method to find a root of p(z), we start with an initial guess z0 = 4 and iterate the formula z1 = z0 - p(z0)/p'(z0) until we reach a desired level of accuracy.
4. We already computed p'(z) in part 2, so we can use the formula to compute z1 as follows:
z1 = z0 - p(z0)/p'(z0)
= 4 - (78 + 10(4) - 20.5(4 - 4)^2 - 2.333(4 - 4)^3)/[6(4)^2 - 28(4)^3 - 10(4)^2 + 2(4) - 8]
= 3.9167
We can continue to iterate using this formula to get better approximations for the root of p(z).
Horner's algorithm is a fast and efficient way to evaluate a polynomial at a particular point. It involves using the distributive property of multiplication to rewrite a polynomial in a nested form, then evaluating the polynomial from the inside out.
In this problem, we will use Horner's algorithm to evaluate p(4) for a given polynomial, find its Taylor series expansion about the point z0 = 4, and then use Newton's method to find an approximation for a root of the polynomial.
Know more about "Horner's algorithm" here:-
https://brainly.com/question/5150902#
#SPJ11
Suppose the profit from the sale of x units of a product is P=6400x−18x^2−400. (a) What levei(s) of production will yield a profit of $359,400 ? (Enter your answers as a comma-separated list. Round your answers to two decimal places.) (b) Can a profit of more than $359,400 be made?
Answers
(a)The levels of production that will yield a profit of $359,400 are approximately 292.36 and 651.64 units. (b)So, it is possible to make a profit of more than $359,400.
(a) To determine the level(s) of production that will yield a profit of $359,400, substitute P=359400 in the equation.6400x−18x^2−400 = 359400Adding 400 to both sides:6400x − 18x² = 359800
Dividing both sides by -2:9x² − 3200x + 179700 = 0
Applying the quadratic formula:
x = (-(-3200) ± √((-3200)² - 4(9)(179700))))/(2(9))
= (3200 ± √(10240000 - 6464400))/18
= (3200 ± √(3785600))/18
= (3200 ± 1946.55)/18x
= 292.36 or 651.64
Thus, the levels of production that will yield a profit of $359,400 are approximately 292.36 and 651.64 units.
(b) To determine if a profit of more than $359,400 can be made, we need to determine the maximum profit by completing the square, and comparing it to $359,400.P=6400x−18x^2−400
Completing the square: P= -18(x - 88.89)² + 710937.2
Maximum profit is $710,937.20, which is more than $359,400.
So, it is possible to make a profit of more than $359,400.
Learn more about quadratic formula here:
https://brainly.com/question/22364785
#SPJ11
Use a permutation expression to solve.
In a race of 48 people, how many different ways can the runners place in 1st, 2nd, and 3rd?
17,296
34,592
103,776
110,592
Answers
Answer:
The answer is 103,776
Step-by-step explanation: I took the k12 test.
Help me with this question.

Answers
Answer:
The equation for the nth term of the arithmetic sequence is:
\(a_{n} = a + (n-1)d\\\)
The \(a_{30}\) is 140
Step-by-step explanation:
"a" represents the first term which is -5.
"d" represents the common difference which is 5.
To find the common difference, just subtract the 2nd and 1st term.
0 - (-5) = 5
Now put the values in the equation:
\(a_{n} = a + (n - 1)d\\a_{n} = (-5) + (n - 1)5\)
We are finding the 30th term so just put 30 to the "n" to help us find the 30th term of the sequence.
\(a_{30} = -5 + (30-1)5\\a_{30} = -5 + (29)5\\a_{30} = -5 + 145\\a_{30} = 140\)
So the 30th term is 140
Tell me which lines to draw to which ( whoever answers correctly gets brainliset )

Answers
Answer:
13. 24ft = 8yd
14. 120in = 10 ft
15. 2 yd = 72 in
16. 5 yd = 180 in
17. 20yd = 60 ft
Step-by-step explanation:
24ft*12 in = 288 inches/36 inches(1yd) = 8yd
120in/12in = 10ft
2yd*36in = 72 in
5yd*36in = 180 in
20yd*36in = 720/12in = 60ft
1ft = 12inches
1 yd = 36 inches
Solve the system of equations using elimination. −3x + 2y = 9 x + y = 12 (−3, 0) (1, 6) (3, 9) (5, 7)
Answers
The system of equations using elimination. −3x + 2y = 9 x + y = 12 is x = 4/7 and y = 48/7
We need to solve the system of equations using elimination method
-3x + 2y = 12....... equation 1
9x + y = 12...........equation 2
Multiply the 2nd equation with 2
18x + 2y = 24 ............equation 3
Now, subtracting equation 3 from equation 1
- 3x - 18x + 2y - 2y = 12 - 24
-21x = 12
x = 12/21 = 4/7
-3(4/7) + 2y = 12
-12/7 + 2y = 12
2y = 12 + 12/7
2y = 96/7
y = 48/7
Therefore, the system of equations using elimination. −3x + 2y = 9 x + y = 12 is x = 4/7 and y = 48/7
To learn more about elimination method refer here
https://brainly.com/question/28405823
#SPJ1
Answer:
(3, 9)
Step-by-step explanation:
I did the test
Solve for w.
–0.05 + 2.3w − 14w = –6.89 − 13.6w
w =
Answers
Answer:
w = -3.6
Step-by-step explanation:
→Add like terms (2.3w and -14 w):
-0.05 + 2.3w - 14w = -6.89 - 13.6w
-0.05 -11.7w = -6.89 - 13.6w
→Add 11.7w to both sides:
-0.05 = -6.89 - 1.9w
→Add 6.89 to both sides:
6.84 = -1.9w
→Divide both sides by -1.9:
-3.6 = w
Answer:
\( \boxed{w = - 3.6} \)
Step-by-step explanation:
\( = > - 0.05 + 2.3w - 14w = - 6.89 - 13.6w \\ \\ = > - 0.05 - 11.7w = - 6.89 - 13.6w \\ \\ = > - 0.05 - 11.7w + 13.6w = - 6.89 \\ \\ = > - 0.05 + 1.9w = - 6.89 \\ \\ = > 1.9w = - 6.89 + 0.05 \\ \\ = > 1.9w = - 6.84 \\ \\ = > w = - \frac{6.84}{1.9} \\ \\ = > w = - 3.6\)
Brand A was $1.25 and Brand B was $1.10. Which is cheaper?
Answers
Answer:
Brand B is cheaper by 15 cents
Step-by-step explanation:
1.25-1.10=0.15
Answer:
brand B
Step-by-step explanation:
brand A=$1.25
brand B=$1.10
subtraction of both brands
1.25-1.10=0.15
brand A is 0.15 expensive than brand B
thus brand B is cheaper
Help please if u can
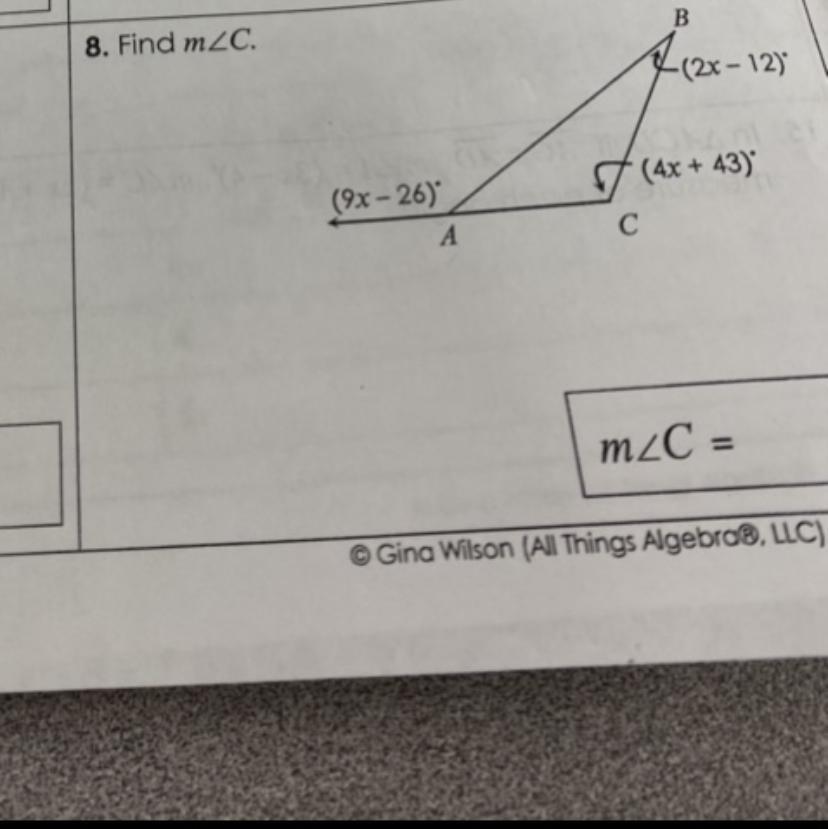
Answers
Answer:
m<C = 119°
Step-by-step explanation:
Create an equation to find the value of x.
(9x - 26)° = (2x - 12)° + (4x + 43)° (exterior angle theorem of a ∆)
Solve for x
9x - 26 = 2x - 12 + 4x + 43
Add like terms
9x - 26 = 6x + 31
9x - 6x = 26 + 31
3x = 57
Divide both sides by 3
x = 19
✔️m<C = 4x + 43
Plug in the value of x
m<C = 4(19) + 43
m<C = 76 + 43
m<C = 119°
1/2=
A=1/3
B=2/3
C=3/4
D=3/6
E=5/6
Answers
Answer:
1/2 = D
Step-by-step explanation:
Let's look on the data we already have.
You can notice that D = 3/6 that equals 1/2
So we can defiantly say that a 1/2 equals D
If m∠AED = 35°, what is m∠ABC?
Answers
The measure of angle ABC is given as follows:
m < ABC = 145º.
What are supplementary angles?Two angles are defined as supplementary angles when the sum of their measures is of 180º.
In a parallelogram, we have that the opposite angles are supplementary.
The opposite angles for this problem are given as follows:
<AED.<ABC.Hence the measure of angle ABC is given as follows:
m < ABC + 35º = 180º.
m < ABC = 145º.
More can be learned about supplementary angles at brainly.com/question/2046046
#SPJ1

Suppose that there are 2n + 1 airports where n is a positive integer. The distances between any two airports are all different. For each airport, there is exactly one airplane departing from it, and heading towards the closest airport. Prove by induction that there is an airport which none of the airplanes are heading towards.
Answers
The method of induction is a mathematical proof technique that involves showing that a statement holds for a base case, and then showing that if it holds for n, it also holds for n+1. This process is repeated until the statement is shown to hold for all positive integers.
This statement can be proven by induction.
Base Case:
For n = 1, there are 3 airports. Let the 3 airports be A, B, and C. If an airplane from airport A is heading towards airport B, then the airplane from airport B must be heading towards airport C, and the airplane from airport C must be heading towards airport A. Hence, there is no airport that none of the airplanes are heading towards.
Inductive Step:
Assume that the statement holds for n = k, where k is a positive integer.
We need to prove that the statement holds for n = k + 1, where there are 2(k + 1) + 1 = 2k + 3 airports.
Let the 2k + 3 airports be A1, A2, ..., A2k + 3. Without loss of generality, let the airplane from airport A1 be heading toward airport A2.
Since the distances between any two airports are all different, we have two cases to consider:
If there exists an airport Ai, such that Ai is the closest airport to A1, then airplanes from Ai must be heading towards A1.
If there is no airport Ai that is closest to A1, then there must be the closest pair of airports, say Ai and Aj, such that Ai is the closest to A1 and Aj is the closest to Ai.
In the first case, none of the airplanes are heading towards Ai, and in the second case, neither Ai nor Aj is the closest airport to any other airport. Hence, in both cases, there is an airport that none of the airplanes are heading towards.
By induction, the statement holds for all positive integers n.
To know more about induction refer to:
brainly.com/question/13079664
#SPJ4
Kelly received two gift cards to her favorite store. One card was worth $25 and the other was
worth $40. She went shopping and used the cards to buy 3 shirts for $9 each and 2 skirts for
$17 each. How much gift card money did she have left?
Answers
$40 + $25 = $65 in gift cards
9 x 3 shirts = $27
$17 x 2 skirts = $34
$65 - 27 - 34 = $4 left
Write a simplified explicit formula for the arithmetic sequence below. Make sure to write all answers in the correct notation. Then find a100.
Given: 9,7,5,3...
Answers
The explicit formula for the arithmetic sequence is aₙ = 11 - 2n, and the 100th term is -189.
The common difference of this arithmetic sequence is -2, since we are subtracting 2 from each term to get the next term. The first term is 9, so the explicit formula for the nth term of this sequence is:
aₙ = 9 + (n - 1)(-2)
Simplifying this expression gives:
aₙ = 11 - 2n
To find a₁₀₀, we simply substitute n = 100 into the formula:
a₁₀₀ = 11 - 2(100) = -189
Therefore, the explicit formula for the arithmetic sequence is aₙ = 11 - 2n, and the 100th term is -189.
Learn more arithmetic here: brainly.com/question/11559160
#SPJ4
Sally's huge dog weighed 145 pounds in 2006 and then weighed 175 pounds in 2018. What was the rate of change in weight?
Answers
Answer:
2.5 pounds per year
Step-by-step explanation:
tandard form of 0.0000428 is
Answers
Answer:
4.28 × 10-5
Step-by-step explanation:
Which subatomic particles are located in the nucleus of an He-4 atom?
Answers
The sub-atomic particles located in the nucleus of an He^4 atom are 2 protons and 2 neutrons.
Helium belongs to double-electronic species, unlike alpha-particles which are devoid of electrons. The two electrons of Helium are accommodated in the 1s orbital, outside the nucleus.
Nucleons are always present in the nucleus of various elements. Nucleons collectively refer to protons and neutrons. In this case, 2 protons and 2 neutrons reside in the nucleus.
The number of protons is always equal to the atomic number of the element. The number of neutrons is always equal to the difference between the mass number and the atomic number of the element.
Learn more about calculating Sub-atomic particles:
https://brainly.com/question/1805828
What is the simplified form of i^15
Answers
Answer:
-i
Step-by-step explanation:
Steven went to the mall with some money. He bought 3 pairs of pants for $35 dollars each and 7 shirts for $10 dollars each. Now he has $25 dollars left. How much money did Steven start with?
Answers
So Steven started with $200
The sum of two numbers is 1. If one number is subtracted from the other, their difference is - 17. Find the numbers.
Answers
Answer:
-17(-)-18=-17+18=1 or -17+18=1
Step-by-step explanation:
if -17 is one number you Add 18.
-17(-)-18=-17+18=1
Answer each question about the following arithmetic series: 12 18 24 30 . . . 198 what is the explicit rule for the arithmetic sequence on which the series is based? an = (n – 1)
Answers
Answer:
12 6
then 32
and 3360
Step-by-step explanation:
The explicit formula is an= 12+ (n-1)6.
What is Arithmetic progression?Arithmetic Progression (AP) is a sequence of numbers in order, in which the difference between any two consecutive numbers is a constant value. It is also called Arithmetic Sequence.
Given:
12 18 24 30 . . . 198
a=12
d= 6
So, an= a + (n- 1)d
an= 12+ (n-1)6
Hence, the explicit formula is an= 12+ (n-1)6.
Learn more about tis concept here:
https://brainly.com/question/16001001
#SPJ2
Probability of an uncertain outcome is a number between 0 and +1, exclusively. True False
Answers
True. Probability of an uncertain outcome is a number between 0 and +1, exclusively.
The probability of an uncertain outcome is a measure of the likelihood that the outcome will occur, and it is always a number between 0 and 1, inclusive. A probability of 0 means that the event is impossible, while a probability of 1 means that the event is certain. Probabilities between 0 and 1 indicate the degree of uncertainty about whether the event will occur or not.
Probabilities cannot be negative or greater than 1, as they represent a proportion of the total possible outcomes. If the probability of an event were negative or greater than 1, it would imply that the event is impossible or certain to occur, respectively, and violate the fundamental laws of probability theory.
Learn more about Probability here
https://brainly.com/question/13604758
#SPJ11
What is the inverse of the function f(x) = 2x + 1?
h(x) = one-halfx – one-half
h(x) = one-halfx + one-half
h(x) = one-halfx – 2
h(x) = one-halfx + 2
f(–2) = g(–2)
f(0) = g(–2)
f(–2) = g(0)
Answers
The inverse of the function f(x) = 2x+1 is (x-1)/2.
What is inverse of function?The output of a function is returned by the inverse function, which also returns the initial value. Consider the inverse relationship between the functions f and g: f(g(x)) = g(f(x)) = x. The initial value is fetched via a function that is its inverse.
Given;
Function, f(x) = 2x + 1.
To find the inverse of the function:
First, let y = f(x)
That is,
y = 2x +1
Then, make x the subject of the equation
y = 2x + 1
To make x the subject of this equation:
First, subtract 1 from both sides
We get
y -1 = 2x
Now, divide both sides by 2.
x = (y-1)/2
Now, rewrite as f⁻¹(x) by replacing y by x.
That is,
f⁻¹(x) = (x-1)/2
Therefore, the inverse of the function f(x) is (x-1)/2.
To learn more about the inverse of function;
https://brainly.com/question/17872426
#SPJ1
Nadya put the data she collected during her survey in a table. Then she found the mean of each of the four rows of data. Population Data 2 4 5 4 5 2 4 2 4 3 4 3 2 4 4 3 4 4 3 2 Find the mean from each row of data. Between what values will the mean of the actual population be found? 3. 2 and 3. 4 3. 2 and 4 3. 4 and 4 3 and 4.
Answers
Table is a way to represent the data of the two or more variable.
The mean of row 1 is 4.The mean of row 2 is 3.The mean of the row 3 is 3.4.The mean of the row 4 is 3.2.All the means lies between 3 and 4. Thus the option 4 is the correct option.
How to read the data from the table?Table is a way to represent the data of the two or more variable.
To read the data from the table look for the value of one variable, and get the resultant value of other variable from the corresponding block.
Given information-
The population date of Nadya's survey is,
Row 1- 2, 4, 5, 4, 5
Row 2- 2, 4, 2, 4, 3
Row 3- 4, 3, 2, 4, 4
Row 4- 3, 4, 4, 3, 2
Mean of the data is the average of values. The mean is the ratio of sum of all the values to the number of values,
The mean of row 1.Row 1- 2, 4, 5, 4, 5
\(m=\dfrac{ 2+ 4+ 5+ 4+ 5}{5}\\m=\dfrac{20}{5}\\m=4\)
The mean of the row 1 is 4.
The mean of row 2.Row 2- 2, 4, 2, 4, 3
\(m=\dfrac{ 2+4+2+4+3}{5}\\m=3\)
The mean of the row 2 is 3.
The mean of row 3.Row 3- 4, 3, 2, 4, 4
\(m=\dfrac{ 4+3+2+4+4+}{5}\\m=3.4\)
The mean of the row 3 is 3.4.
The mean of row 4.Row 4- 2, 4, 5, 4, 5
\(m=\dfrac{ 3+4+4+3+2}{5}\\m=3.2\)
The mean of the row 4 is 3.2.
Hence,
The mean of row 1 is 4.The mean of row 2 is 3.The mean of the row 3 is 3.4.The mean of the row 4 is 3.2.All the means lies between 3 and 4. Thus the option 4 is the correct option.
Learn more about the data table here;
https://brainly.com/question/15602982
Can someone help with an explanation please

Answers
The percentage of the total hours did Andrea work is,
⇒ 27.1%
What is mean by Percentage?A number or ratio that can be expressed as a fraction of 100 or a relative value indicating hundredth part of any quantity is called percentage.
Given that;
Total number of hours to work is,
⇒ 5.8 + 8.1 + 7.3 + 8.7 hours
⇒ 29.9 hours
Here, Andre work 8.1 hours.
Hence, The percentage of the total hours did Andrea work is,
⇒ 8.1 / 29.9 × 100
⇒ 27.1%
Thus, The percentage of the total hours did Andrea work is,
⇒ 27.1%
Learn more about the percent visit:
https://brainly.com/question/24877689
#SPJ1