Answers
Answer:
your answer will be x=1.13504161
9514 1404 393
Answer:
{-1.47, 1.14}
Step-by-step explanation:
The solution to ...
ax^2 +bx +c = 0 is ...
\(x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\)
Filling in the values a=3, b=1, c=-5, the solutions are ...
\(x=\dfrac{-1\pm\sqrt{1^2-4(3)(-5)}}{2(3)}=\dfrac{-1\pm\sqrt{61}}{6}\\\\\boxed{x\approx\{-1.47,1.14\}}\)

Related Questions
Please help not sure how to do thIs see attached below

Answers
Answer:
7 in 1/2 for Y and 6 in 1/2 for X
Step-by-step explanation:
you can not go up nine so split it in half and add them on to X Y
and PS I am in 7th grade I tried my best and do you want to be friends ? my name is Ayden Hickle.
PLEASE HELP IM DESPERATE precalculus. also 50 points!! please god help

Answers
Answer:
For B thru F these options will vary but here how you do it
B. Step 1 Draw the 4 Quadrants.
Then Draw the Triangle in the lower right quadrant which we call quadrant 4. Label the X axis as Adjacent and positive. Label the Y axis as Opposite and negative. Label the Slanted side as the hypotune and AS POSITVE SINCE HYPOTENUSE IS ALWAYS POSITIVE.
FOR C. IN QUADRANT 2, PLOT A POINT AT 0,12 AND AT (-5,0). CONNECT THE DOTS AND IT FORMS A TRIANGLE. Label the X axis as adjacent and negative and the y axis as positve and opposite and label the slanted side hypotunese and positive.
FOR D Draw a straight line along the x axis then draw a slanted line passing through (5,-1). In between them put the theta symbol in there.
The labeling is the same for C.
For E. Since tan must be positve and secant must be positve, our triangle must be in the 1st Quadrant. Draw any right triangle as long it is in the first quadrant
The x axis is adjacent and positve. The y axis is opposite and positve. The hypotenuse is the slanted side and it is positve.
For F. Since sin is negative and cos is positve the triangle is in the 4th quadrant. Draw any triangle in the 4th quadrant and the labeling is the same for Problem B.
2. We can find the sec of cos by flipping cosine.
\( \cos( \frac{x}{y} ) = \sec( \frac{y}{x} ) \)
\( \cos( \frac{1}{2} ) = \sec(2 ) \)
Sec is 2.
To find the cotangent, first let find the sin then tan.
We can use the identity
\( \cos( {theta}^{2} ) + \sin( {theta}^{2} ) = 1\)
Let plug in the number
\( \cos( \frac{ {1}^{2} }{{2}^{2} } ) + \sin(x {}^{2} ) = 1\)
\( \cos( \frac{1}{4} ) + \sin(x {}^{2} ) = 1\)
\( \sin(x {}^{2} ) = 1 - \frac{1}{4} \)
\( \sin(x {}^{2} ) = \frac{3}{4} \)
\( \sin(x) = \frac{ \sqrt{3} }{ \sqrt{4} } \)
\( \sin(x) = \frac{ \sqrt{3} }{2} \)
Since sin is negative, sin x=
\( - \frac{ \sqrt{3} }{2} \)
Now let apply the formula
\( \frac{ \sin(x) }{ \cos(x) } = \tan(x) \)
\( \frac{ \frac{ - \sqrt{3} }{2} }{ \frac{1}{2} } = \tan(x) \)
\( - \sqrt{3} \)
Now let find cotangent we can the reciprocal of
tan.
\( \tan= - \sqrt{3} \)
\( \cot = - \frac{1}{ \sqrt{3} } \)
Rationalize denominator
\( \frac{ - 1}{ \sqrt{3} } \times \frac{ \sqrt{3} }{ \sqrt{3} } = \frac{ \sqrt -{ 3} }{3} \)
cotangent equal
\( - \frac{ \sqrt{ 3} }{3} \)
1. A new compact has a sticker price of $14500. Options add another $982. Destination charges are $592. Dealer preparation is 5% of the total price. Sales tax is 7%. Tag fee is $145. Title fee is $45. What is the total price of the vehicle?
2. The selling price of a used car is $8850. Trade in allowance is $1500. Tax is 8%. Tag fee is $130. Title fee is $35. Finance charges are 9.5% annual simple interest. What is the total price of the financed amount? What are the total finance charges? What are the monthly payments if the vehicle is financed for 3 years? What is the total deferred price of the car?
3. The total deferred price of a car is $28000. After a down payment of $2100, the monthly payments are $380. How long is the financing agreement?
4. Stanley bought a new car with a sticker price of $19200. The dealer agreed to a 6% discount. The sales tax was 8% of the selling price. The tag fee was $65, and the title fee was $45. What is the total price of the car? The interest rate is 9% for financing the car for 5 years. What is the total deferred price after all the payments were made?
5. Mark bought a truck with a sticker price of $23000 plus additional options totaling $3500. He received a 4% discount and a $1500 trade-in allowance. The tax was 7%, tag fee was $125, and title fee was $75. He bought an extended warranty for $700, which was financed into the total cost of the truck. The interest rate was 6.5% for 5 years. How much are the monthly payments?
Answers
The total price of the vehicle would be $18,192.88.
The total deferred price of the car would be $11,191.60.
The length of the financing agreement is 68 months .
The total deferred price after the payments was $19,601.84.
The monthly payments would be $516.92.
How to find the price of the vehicle ?Subtotal = Base price + Options + Destination charges
Subtotal = $14,500 + $982 + $592 = $16,074
Dealer preparation = 5% of subtotal
Dealer preparation = 0.05 x $16,074 = $803.70
Sales tax = 7% of subtotal
Sales tax = 0.07 x $16,074 = $1,125.18
Total price = Subtotal + Dealer preparation + Sales tax + Tag fee + Title fee
Total price = $16,074 + $803.70 + $1,125.18 + $145 + $45 = $18,192.88
How to find the total deferred price ?Tax = 8% of selling price = 0.08 x $8,850 = $708
Tag fee = $130
Title fee = $35
Total amount financed = Amount financed + Tax + Tag fee + Title fee = $7,350 + $708 + $130 + $35 = $8,223
Annual interest rate = 9.5%
Number of years financed = 3
Total finance charges = $8,223 x 0.095 x 3 = $2,341.595
Total financed amount = $8,223 + $2,341.595 = $10,564.595
Monthly payments = Total financed amount / (Number of years financed x 12 months) = $10,564.595 / (3 x 12) = $293.4615
Total deferred price = Selling price + Total finance charges = $8,850 + $2,341.595 = $11,191.595
How to find the length of the financing agreement ?Total deferred price = $28,000
Down payment = $2,100
Total amount financed = Total deferred price - Down payment = $28,000 - $2,100 = $25,900
Monthly payments = $380
Number of months = Total amount financed / Monthly payments = $25,900 / $380 = 68.16
The financing agreement is approximately 68 months long.
How to find the deferred price after the payments ?Sticker price = $19,200
Discount = 6% of sticker price = 0.06 x $19,200 = $1,152
Selling price = Sticker price - Discount = $19,200 - $1,152 = $18,048
Sales tax = 8% of selling price = 0.08 x $18,048 = $1,443.84
Total price = Selling price + Sales tax + Tag fee + Title fee = $18,048 + $1,443.84 + $65 + $45 = $19,601.84
How to find the monthly payments ?Using the formula for monthly payments on a loan:
P = (PV x r x (1 + r)^ n) / ((1 + r) ^ n - 1)
= ($26,515.80 x 0.005265 x (1 + 0.005265) ^ 60 ) / ((1 + 0.005265) ^ 60 - 1) = $516.92
Find out more on monthly payments at https://brainly.com/question/27926261
#SPJ1
3 2/5 divided by 1 1/5 pleaseeee help its due on may 24
Answers
Answer:
2.83333333333
Step-by-step explanation:
(3 2/5) / (1 1/5) = 2.83333333333
Answer:
85/30 or 2.833333333
Step-by-step explanation:
When dividing fractions, you must find the reciprocal of the second number and multiply it as usual.
It is also much easier to solve after you convert these numbers to improper fractions.
In this case,
3 2/5 = 17/5
1 1/5 = 6/5
17/5 ÷ 6/5
17/5 x 5/6
85/30 (17/6 reduced)
or
2.83333333333333333333
y=x^2-2x+7
i need help finding the axis of symmetry,the domain, the y-intercept and x intercept

Answers
The axis of symmetry is at x = 1, the domain is (-∞, +∞), the y-intercept c is at 7 and x intercept is not applying .
Explain about the features of parabolic function?A parabolic function is one that satisfies the formula f(x) = ax2 + bx + c and, when represented graphically in two dimensions, has the shape of a parabola. Any quadratic equation with just a second degree in x is the equation for a parabolic function.
The following characteristics define a basic parabola:
The y-axis, a symmetry axis, is where it is symmetric.At the origin, marking the minimal turning point, y has its minimum value. It is sometimes referred to as the parabola's vertex.The parabola's arms are infinitely long.Thus, from the given graph the value are obtained as:
the axis of symmetry is at x = 1, the domain is (-∞, +∞), the y-intercept c is at 7 and x intercept is not applying .Know more about parabolic function
https://brainly.com/question/30281619
#SPJ1
x=y=3
2x - 2y = -6
5x + 2y = -7
10x + 4y = - 14
3y - 6x = 3
4x - 3y = - 2
3y - 6x =
-3
4x - 2y = - 2
no solution
one solution
infinite number of solutions

Answers
Note that the system of equations matched with their correct descriptions is given as follows:
1) x=y-3
2x - 2y = -6
Infinite Number of Solutions
2)5x + 2y = -7
10x + 4y = - 14
Infinite Number of Solutions
3) 3y - 6x = 3
4x - 3y = - 2
One solution
4) 3y - 6x =-3
4x - 2y = - 2
No solution
What is the Justification for the above response?1)
Using substitution methods, let's solve for
x=y-3.................. (1)
2x - 2y = -6.........(2)
Let's keep both expressions as the subject of x
x=y-3 (Given)
2x - 2y = -6
Add 2y to both sides to isolate x
2x - 2y + 2y = -6 + 2y
2x = -6 + 2y (divide both sides by 2
x = y - 3 .........................(3)
Notice the similarity with (1)
Subsitite (3) into (2) 2x - 2y = -6
That is:
2(y - 3) - 2y = -6
⇒ -6 = -6 (Add 6 to both sides)
⇒ 0=0
Given the result above, the system of equations has an infinite number of solutions.
2)
Use the elimination method to solve the system of equations:
5x + 2y = - 7
10x + 4y = - 14
Equation 1 is in the correct ax + by format.
Equation 2 is in the correct ax + by format.
Step 1 - Multiply Equation 1 by 10:
10 * (5x+2y=-7) --> 50x + 20y = -70
Step 2 - Multiply Equation 2 by 5:
5 * (10x+4y=-14) --> 50x + 20y = -70
Step 3 - subtract Revised Equation 2 from Revised Equation 1:
50x + 20y = -70
-(50x + 20y = -70)
------------------------------
20y - 20y = -70 - -70
Step 4 - simplify and solve for y:
0 = 0
Given the above result, the system of equations has an infinite number of solutions
3)
3y - 6x = 3 .....(1)
4x - 3y = - 2 .....(2)
Solving by elimination, adding both equations will eliminate y
- 6x + 3y = 3
4x - 3y = - 2
-2x = 1
Thus, solving for x: (Divide both sides by -2)
x = -1/2
Put x back into (1)
- 6(-1/2) + 3y = 3
make Y the subject of the formula
3y + 3 = 3
3y = 3-3
y = 0/3
y = 0
Since y=0 and x = -1/2, we can state that there is only one solution.
4)
3y - 6x =-3 ......(1)
4x - 2y = - 2 ......(2)
To solve my elimination, multiply the first equation by 2,and multiply the second equation by 3.
Equation 1 is in the correct ax + by format.
Equation 2 is in the correct ax + by format.
Step 1 - Multiply Equation 1 by 2:
2 * (3y-6x=-3) --> 6y - 12x = -6
Step 2 - Multiply Equation 2 by -3:
-3 * (4x-2y=-2) --> 6y - 12x = 6
Thus: Adding the results, we have
6y - 12x = -6
+
6y - 12x = 6
12y = 0
y = 0/12
y = 0
Thus, there is no solution for this system of equations.
Learn more about the system of equations:
https://brainly.com/question/90105
#SPJ1
The radius of a cylindrical water tank is 6.5 ft, and it’s height is 9 ft. What is the volume of the tank? Use the value 3.14 for n, and round your answer to the nearest whole number. Be sure to include the correct unit in your answer.
Answers
Given: The radius of a cylindrical water tank is 6.5 ft, and its height is 9 ft.
Required: To determine the volume of the tank.
Explanation: The volume of a cylinder of height h and radius r is-
\(V=\pi r^2h\)Here we have,
\(\begin{gathered} r=6.5\text{ ft} \\ h=9\text{ ft} \end{gathered}\)Hence, the volume of the tank is-
\(V=3.14\times(6.5)^2\times9\)Further simplifying as-
\(\begin{gathered} V=1193.985\text{ ft}^3 \\ V\approx1194\text{ ft}^3 \end{gathered}\)Final Answer: The volume of the tank is 1194 cubic ft.
you had eight hours until you have to be on set if you will spend 3/4 of an hour driving to the TV station how much time does that leave you to get everything ready
Answers
Answer:
7 hours and 15 minutes
Step-by-step explanation:
8 - 3/4 = 7 1/4 hours
For every 5 cars in a parking lot there are 6 trucks. What is the ratio of cars to trucks in the parking lot?
Answers
Answer:
The answer is 5:6 if you need to simply then it would be 10:12
Step-by-step explanation
Hope this helps!
Answer:
5:6 10:12
Step-by-step explanation:
5:6 10:12
Out of 20 people how many would you expect to say that they like all seasons
Answers
Answer:
None
Step-by-step explanation:
Truly, I'm not sure what type of problem this is, but most people don't favor all the seasons. If there is more to the problem, I would be glad to help further.
Answer:
One possible way to estimate how many people out of 20 would say that they like all seasons is to use a simple random sample. A simple random sample is a subset of a population that is selected in such a way that every member of the population has an equal chance of being included. For example, one could use a random number generator to assign a number from 1 to 20 to each person in the population, and then select the first 20 numbers that appear. The sample would then consist of the people who have those numbers.
Using a simple random sample, one could ask each person in the sample whether they like all seasons or not, and then calculate the proportion of positive responses. This proportion is an estimate of the true proportion of people in the population who like all seasons. However, this estimate is not exact, and it may vary depending on the sample that is selected. To measure the uncertainty of the estimate, one could use a confidence interval. A confidence interval is a range of values that is likely to contain the true proportion with a certain level of confidence. For example, a 95% confidence interval means that if the sampling procedure was repeated many times, 95% of the intervals would contain the true proportion.
One way to construct a confidence interval for a proportion is to use the formula:
p ± z * sqrt(p * (1 - p) / n)
where p is the sample proportion, z is a critical value that depends on the level of confidence, and n is the sample size. For a 95% confidence interval, z is approximately 1.96. For example, if out of 20 people in the sample, 12 said that they like all seasons, then the sample proportion is 0.6, and the confidence interval is:
0.6 ± 1.96 * sqrt(0.6 * (1 - 0.6) / 20)
which simplifies to:
0.6 ± 0.22
or:
(0.38, 0.82)
This means that we are 95% confident that the true proportion of people who like all seasons in the population is between 0.38 and 0.82. Therefore, based on this sample and this confidence interval, we would expect between 8 and 16 people out of 20 to say that they like all seasons in the population.
MARK AS BRAINLIEST!!!
2 cents using dollar symbols
Answers
answer:
$0.02
-- let me know if you have any questions regarding this.
is your answer
PLEASE HELP TIMER!!!!!!!!!!!!!

Answers
Answer:
Answer: -3/2
Step-by-step explanation:
#KEEPSAFE
#GOODLUCK
#STUDYWELL
A quadratic equation, y = ax^2 - 6x + 10, has exactly one real root. Calculate the value of a.
Answers
Answer:
a = 0.9
Step-by-step explanation:
For the quadratic equation \(\boxed{ax^2 + bx + c = 0}\) to have exactly one real root, the value of its discriminant, \(\boxed{b^2 - 4ac}\), must be zero.
For the given equation:
\(y = ax^2 - 6x + 10\),
• a = a
• b = -6
• c = 10.
Substituting these values into the formula for discriminant, we get:
\((-6)^2 - 4(a)(10) = 0\)
⇒ \(36 - 40a = 0\)
⇒ \(36 = 40a\)
⇒ \(a = \frac{36}{40}\)
⇒ \(a = \bf 0.9\)
Therefore the value of a is 0.9 when the given quadratic has exactly one root.
#11-14 Answers are on the side

Answers
Dividing the sum of (7/8) (15/4) (1/12) by their multiplication gives _________
Answers
The Division of the sum of (7/8), (15/4), and (1/12) by their multiplication is (2712/168).
To find the division of the sum of (7/8), (15/4), and (1/12) by their multiplication, we first need to calculate the sum and multiplication of the given fractions.
The sum of the fractions is:
(7/8) + (15/4) + (1/12)
To add these fractions, we need a common denominator. The least common multiple of 8, 4, and 12 is 24. Let's convert each fraction to have a denominator of 24:
(7/8) = (21/24)
(15/4) = (90/24)
(1/12) = (2/24)
Now we can add the fractions:
(21/24) + (90/24) + (2/24) = (113/24)
The multiplication of the fractions is:
(7/8) * (15/4) * (1/12)
To multiply fractions, we multiply the numerators and denominators:
(7*15*1) / (8*4*12) = (7/96)
Now we can divide the sum of the fractions by their multiplication:
(113/24) / (7/96)
To divide fractions, we multiply the first fraction by the reciprocal of the second fraction:
(113/24) * (96/7) = (2712/168)
Therefore, the division of the sum of (7/8), (15/4), and (1/12) by their multiplication is (2712/168).
For more questions on Division .
https://brainly.com/question/30340100
#SPJ8
In circle M below, diameter AC, chords AB and BC, and radius MB
are drawn.

Answers
The statement which is not true about the circle M is ∆ABM is isosceles.
The correct answer choice is option 2.
Which statement is not true?Based on the circle M;
diameter AC,
chords AB and BC,
radius MB
Isosceles triangle: This is a type of triangle which has two equal sides and angles.
Equilateral triangle is a triangle which has three equal sides and angles.
Hence, ∆ABM is equilateral triangle.
Read more on triangles:
https://brainly.com/question/1058720
#SPJ1
Let x and y be functions of time t such that the sum of x and twice y is constant. Which of the following equations describes the relationship between the rate of change of with respect to time and the rate of
change of with respect to time?
A) dx/dt=2dy/dt
B) dx/dt=-2dy/dt
C) 2dx/dt+dy/dt=0
D) dx/dt + 2dy/dt=K, where K is a function of t
Answers
B) dx/dt=-2dy/dt is the relation of the rate of change for the conditon given in the question.
what is rate of change?Rate of change is a measure of how quickly a variable is changing. It is often represented by the symbol "d/dt" or "∆y/∆x" and is calculated by finding the ratio of the change in one variable to the change in another variable.
Given :
x + 2y =k
where k is a constant
differentiating above equation with respect to time we get
=> dx/dt + 2dy/dt =dk/dt
=> dx/dt + 2dy/dt =0
=> dx/dt = -2dy/dt
so Option B) dx/dt=-2dy/dt is correct option for the above problem
To know more about Rate of change click on below link:
https://brainly.com/question/29518179#
#SPJ4
The body temperatures of a group of healthy adults have a bell-shaped distribution with a mean of 98.27°F and a standard
deviation of 0.54°F. Using the empirical rule, find each approximate percentage below.
a. What is the approximate percentage of healthy adults with body temperatures within 1 standard deviation of the mean, or
between 97.73 °F and 98.81°F?
Answers
Answer: follow this you'll be able to solve it
Step-by-step explanation: mean = 98.11F
standard deviation = 0.56F
99.79 – 98.11 = 1.68 = 3 standard deviations
96.43 – 98.11 = –1.68 = –3 standard deviations
96.43F and 99.79F are 3 standard deviations from the mean 98.11F.
By the empirical rule we know that 99.7% of the data lies within 3 standard deviation of the mean.
Approximately 68% of healthy adults in this group have body temperatures within 1 standard of the mean, or between 97.55F and 98.67F.
GIVING BRAILIEST PLEASEE!! Given an exponential function for compounding interest, A(t) = P(0.82)t, what is the rate of decay?
A. 18%
B. 8%
C. 0.82%
D. 82%
Answers
Answer:A
Step-by-step explanation:
To find the rate of decay, we need to use the formula A(t) = P(0.82)^t, where A(t) is the amount after t years, P is the initial amount, and 0.82 is the decay factor.
The decay factor is equal to 1 minus the decay rate, so we can solve for the decay rate as follows:
0.82 = 1 - r
r = 1 - 0.82
r = 0.18
Therefore, the rate of decay is 18%, which corresponds to answer choice A.
Answer:
A
Step-by-step explanation:
Select the correct answer.
Which sentence correctly describes a data set that follows a normal distribution with a standard deviation of 4 and a mean of 14?
68% of the data points lie between 10 and 14.
68% of the data points lie between 8 and 12.
68% of the data points lie between 10 and 18.
68% of the data points lie between 10 and 16.
Answers
Answer:
68% of the data points lie between 10 and 18.
Step-by-step explanation:
one standard deviation to left of mean = 14 - 4 =10
one standard deviation to right of mean = 14 + 4 = 18
68% of data is in this region.
so the answer is 68% of the data points lie between 10 and 18.
A human gene carries a certain disease from the mother to the child with a probability rate of 34%. That is, there is a 34% chance that the child becomes infected with the disease. Suppose a female carrier of the gene has three children. Assume that the infections of the three children are independent of one another. Find the probability that at least one of the children get the disease from their mother.
Answer the following questions:
State the complement of the event "At least one of the children get the disease from their mother".
Find the probability of the complement. Round your answer to four decimals
Find the probability that at least one of the children get the disease from their mother.
Answers
Answer:
The probability that at least one of the children get the disease from their mother is 0.7125.
Step-by-step explanation:
We are given that a human gene carries a certain disease from the mother to the child with a probability rate of 34%.
Suppose a female carrier of the gene has three children. Assume that the infections of the three children are independent of one another.
Let Probability that children get the disease from their mother = P(A) = 0.34
SO, Complement of the event "At least one of the children get the disease from their mother"= P(A') = 1 - P(A)
where A' = event that children do not get the disease from mother.
So, P(A') = 1 - P(A) = 1 - 0.34 = 0.66
Now, probability that at least one of the children get the disease from their mother = 1 - Probability that none of the three children get disease from their mother
= 1 - P(X = 0)
= 1 - (0.66 \(\times\) 0.66 \(\times\) 0.66)
= 1 - 0.2875 = 0.7125
16) Solve for side AB.
AB-
Round your answer to the nearest hundredth.
A) 5.45
B) 6.45
C) 7.45

Answers
Answer:
AB= 7.45
Anwer C)
Step-by-step explanation:
Cos (angle) = Nearest side / Huypothenuse
Cos(20) = 7 / AB
Cos(20) * AB = (7 /AB) * AB
Cos (20) * AB = 7
(Cos(20) *AB) / Cos(20) = 7 / Cos(20)
AB = 7 / cos(20)
AB= 7.45
In order to find the hypotenuse, we can use the trigonometric function “cosine”,
since.
Cosine =
Adjacent side (which is 7) / hypotenuse
Cos(50) = 7 / AB
AB = 7 / Cos(50)
AB = 10.89006678802289
AB ≈ 10.89
Have a good day ^^
someone please help!!

Answers
Answer:
3.357 (idk how your teacher wants u to round)
Step-by-step explanation:
I plugged in 51 so the equation looked like this:
\(14x+4=51\)
then solve by subtracting 4 from the equation and from the answer so it changes to:
\(14x=47\)
then divide 14 from both sides and you get:
\(x= 3.35714286\)
Marissa launches a toy rocket in her backyard. The path of the rocket is
modeled by the equation h = 18t - 3t, where h is the height in feet, and t is the
time in seconds since the rocket was launched.
Answers
Answer:
maybe u should have paid attention in class buddy
Step-by-step explanation:
L
Kai is swinging on a trapeze in a circus show. The horizontal distance between Kai and the edge
of the stage, in meters, is modeled by D(t) where t is the time in seconds. The function is
graphed below, along with one segment highlighted.
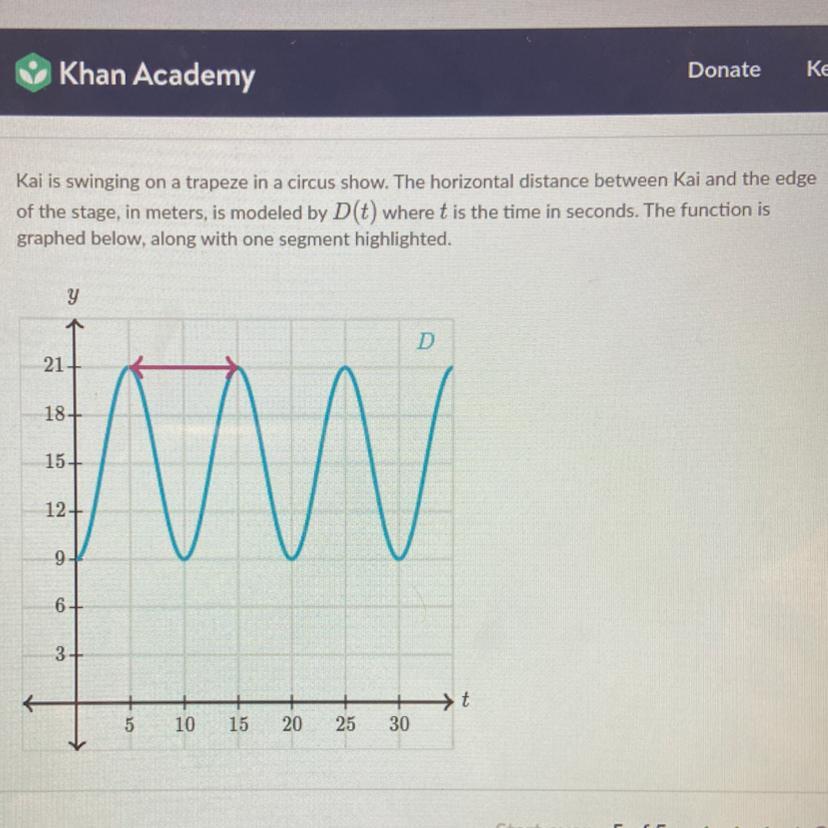
Answers
The sinusoidal expression of the function is D(t) = -cos(3t)
What is sinusoidal expression?A sinusoidal alternating current can be represented by the equation i = I sin ωt, where i is the current at time t and I the maximum current. In a similar way we can write for a sinusoidal alternating voltage v = V sin ωt, where v is the voltage at time t and V the maximum voltage.
here, we have to,
to determine the sinusoidal expression:
When he pushes off, he is 1 m behind the center.
This means that:
Amplitude, a = 1.
But we use, a = -1 because he is behind
The graph has a minimum point at (0,-1) and then intersects its midline at (π/6, 0).
So, the period B is: 2π/B = 4 * π/6 and the vertical shift (d) is 0
Simplify 2π/B = 4 * π/6
2π/B = 2π/3
By comparison, we have:
B = 3
The function is given as:
a cos(Bt) + d
Substitute the calculated values
D(t) = -cos(3t)
Hence, the sinusoidal expression of the function is D(t) = -cos(3t)
Read more about sinusoidal expressions at:
brainly.com/question/16653126
#SPJ1
Answer:
period and he completes a swing in ten seconds
A TV is 20% off the original price amount is $180. What is the original amount?
Answers
Answer: $200
Step-by-step explanation: $200=100% so then $200-20%=$180=80%
Answer:
9005
Step-by-step explanation:
180$ divided by 20% is 900$
a farmer has a total of 7815 beet plants. she wants to plant 40 beet plants in each row. she does the following work in long divison:

Answers
Answer:
D
Step-by-step explanation:
100 points will mark brainliest

Answers
Answer:
A is the answer
Step-by-step explanation:
if its wrong than its C
Look at this alternative hypothesis: Consumer satisfaction ratings of luxury cars is lower than satisfaction ratings of economy cars. The t-value for this alternative hypothesis is 1.99, and the degrees of freedom (df) = 37. Using the calculator (https://www.socscistatistics.com/pvalues/tdistribution.aspx), what is the p-value for this alternative hypothesis? <.0001 .027 .054 .973 .946
Answers
the p-value for this alternative hypothesis is 0.054
The p-value is the probability of obtaining a test statistic as extreme or more extreme than the one observed, assuming that the null hypothesis is true. In this case, the null hypothesis is that there is no difference in consumer satisfaction ratings between luxury and economy cars. The alternative hypothesis is that the satisfaction ratings for luxury cars are lower than those for economy cars.
Using the given t-value of 1.99 and degrees of freedom of 37, we can calculate the p-value using the t-distribution calculator. The p-value obtained is 0.0554, which is larger than the commonly used significance level of 0.05. This means that we do not have sufficient evidence to reject the null hypothesis and conclude that there is a significant difference in consumer satisfaction ratings between luxury and economy cars. Therefore, the correct answer is (c) 0.054.
To learn more about probability:
https://brainly.com/question/30034780
#SPJ4
Mrs alvares rents skis and poles for 3 days what is the total cost of rental

Answers
The total cost of rents is $180.
In the given table,
The cost of skis per day = $48
The cost of pole per day = $12
Now since given that,
Alveres rents for 3 days
Therefore,
The cost of skis for 3 days = $48 x 3
= $144
The cost of pole for 3 days = $12 x 3
= $36
To find the total cost of rental,
Adding the cost of 3 days of skis and cost of 3 days of poles,
Hence,
Total cost of rents = $144 + $36
= $180
Learn more about the addition visit:
https://brainly.com/question/25421984
#SPJ1
