whats 35 divided my 68
Answers
Related Questions
Please answer with formula and how to find it

Answers
Radius is the distance in a straight line from the centre of the circle to its circumference. The diameter is twice the radius. Therefore, radius and diameter of the circle are 7 and 14 yards respectively.
How to find area of a circle?The above figure is a circle. The area of the circle is given as 49π yard squared. The question want us to find the radius and diameter of the circle.
Hence,
area of a circle = πr²
where
r = radius of a squareTherefore,
area of the circle = 49π
Hence,
49π = π × r²
divide both sides by π
r² = 49
square root both sides
r = √49
r = 7 yards
The diameter of a circle is twice the radius.
Hence,
diameter of the circle = 7 × 2 = 14 yards
learn more on area here: https://brainly.com/question/28642423
#SPJ1
I need some help with my math please

Answers
( 31.2u + 0.2 v ) is expression represents the perimeter of rectangle .
What is rectangle short answer?
A rectangle is a sort of quadrilateral with parallel sides that are equal to one another and four vertices that are all 90 degrees apart. Because of this, it is also known as an equiangular quadrilateral. Because the opposite sides of a rectangle are equal and parallel, it can also be referred to as a parallelogram.length of rectangle = ( 7.2u + 9.9v)
width of rectangle = ( 8.4u - 9.8v)
perimeter of rectangle = 2( l + b )
= 2 ( 7.2u + 9.9v + 8.4u - 9.8v )
= 2 ( 7.2u + 8.4u + 9.9v - 9.8v )
= 2 ( 15.6u + 0.1v )
= ( 31.2u + 0.2 v )
Learn more about rectangle
brainly.com/question/15019502
#SPJ13
(Using the table provided)
"Which employees does this information cover?
Give a full description of age, type of worker and who it is not for.
------------------------
ASAP!!!!!!!! I really need hep with this please! it's due tonight! :(

Answers
The employees represented by the information are employees between under 16 years and adults, and the salaries of these workers
How to determine the employees the information cover?The given parameter is the table of values
From the given table of values, we have the following four columns or fields:
ClassificationWeeklyHourly (full time and part-time)Casual (includes 20% loading)Remove the items in brackets
ClassificationWeeklyHourly CasualUnder the classification column, we have the fields under 16 years to adult.
The other columns represent the salaries of the workers
Hence, the employees represented by the information are employees between under 16 years and adults, and the salaries of these workers
Read more about table of values at:
https://brainly.com/question/24040786
#SPJ1
\(\huge \dag \sf{Answer \: it}\)
Refer to attachment.
Note: Spams not allowed.
Don't Copy
If you don't know the answer don't answer
Need Answer with explanation.
Thank You!
![[tex]\huge \dag \sf{Answer \: it}[/tex]Refer to attachment.Note: Spams not allowed. Don't Copy If you](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/LBDqpmvIdPEaSnIj17EGnH0Wj6Gn1s9Z.jpeg)
Answers
Answer:
\(option \: (b) \: is \: ur \: answer \: to \: the \: question \: \)
\(to \: know \: the \: answer \: with \: proof\)
\(refer \: to \: the \: above \: attatchment\)
\(f = \frac{rn}{1 - r} \)
![[tex]\huge \dag \sf{Answer \: it}[/tex]Refer to attachment.Note: Spams not allowed. Don't Copy If you](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/jGEnrQYjdm9kFAFG0tcUMTL8YnSiLGlR.jpeg)
\(\huge \tt༆ Answer ༄\)
The required expression is ~ B
\( \boxed{ \sf \: F = \dfrac{ RN }{ 1 - R} }\)
Refer to the attachment for Solution ~
![[tex]\huge \dag \sf{Answer \: it}[/tex]Refer to attachment.Note: Spams not allowed. Don't Copy If you](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/zMSDguQKtKtAmEFp4Nq7BHtmDbA45ryN.jpeg)
Fred's Fruit Stand has 252 pounds of fruit and sells 2 7/8 pounds per hour. Gary's grocery Store has 285 pounds of fruit and sells 3 1/3 pounds per hour. How many hours until they have the same amount of fruit left?
Answers
Answer:
72.1 hours
Step-by-step explanation:
Let the number of hours be represented as: x
Fred's Fruit Stand has 252 pounds of fruit and sells 2 7/8 pounds per hour.
Convert 2 7/8 pounds to decimal = 2.875pounds
Hence:
252 - 2.875x
Gary's grocery Store has 285 pounds of fruit and sells 3 1/3 pounds per hour.
Convert 3 1/3 pounds to decimal = 3.333 pounds
Hence:
285 - 3.333x
How many hours until they have the same amount of fruit left?
This calculated by equating both equation together
252 - 2.875x = 285 - 3.333x
Collect like terms
-2.875x + 3.333x = 285 - 252
0.458x = 33
x = 33 / 0.458
x = 72.052401747 hours
x ≈ 72.1 hours
They would have the same amount of fruit left after 72.1 hours
The diagram shows the distance
between three towns.
12 miles
Ashton
Lees
Oldham
Brian drives from Ashton to Lees and
then to Oldham.
He drives from Ashton to Lees at
an average speed of 40 mph.
He drives from Lees to Oldham at
an average speed of 30 mph.
Work out Brian's average speed for
the whole journey from Ashton to
Oldham.

Answers
Thus, Brian's average speed for the whole journey from Ashton to Oldham is 34.29 mph.
What is average?Average, also known as mean, is a measure of central tendency in statistics that represents the typical value of a set of numbers. It is calculated by adding up all the numbers in the set and then dividing the sum by the total number of values in the set. For example, if you want to
Given by the question.
To calculate the average speed of Brian's whole journey, we need to use the formula:
average speed = total distance ÷ total time
We know the distance between Ashton and Lees is 12 miles, and we also know the speed at which Brian drove this part of the journey: 40 mph. Using the formula:
time taken = distance ÷ speed
we can calculate that it took Brian:
time taken from Ashton to Lees = 12 miles ÷ 40 mph = 0.3 hours
We also know the distance between Lees and Oldham is 12 miles, and the speed at which Brian drove this part of the journey: 30 mph. Again using the formula:
time taken from Lees to Oldham = 12 miles ÷ 30 mph = 0.4 hours
So, the total distance Brian covered from Ashton to Oldham is:
total distance = distance from Ashton to Lees + distance from Lees to Oldham
total distance = 12 miles + 12 miles = 24 miles
The total time Brian spent on the journey is:
total time = time taken from Ashton to Lees + time taken from Lees to Oldham
total time = 0.3 hours + 0.4 hours = 0.7 hours
Now we can use the formula for average speed:
average speed = total distance ÷ total time
average speed = 24 miles ÷ 0.7 hours
average speed = 34.29 mph
To learn more about speed:
https://brainly.com/question/28224010
#SPJ1
a person 12 feet from a jetski, it is 100 decibels loud. how loud is the jetski when the person is 42 feet away?
Answers
When the person is 42 feet away from the jetski, the sound intensity is approximately 87.1 decibels.
To answer this question, we need to use the inverse square law of sound intensity, which states that the intensity of a sound decreases with the square of the distance from the source.
1. Identify the initial distance (D1) and initial decibel level (L1): In this case, D1 = 12 feet and L1 = 100 decibels.
2. Identify the final distance (D2): In this case, D2 = 42 feet.
3. Calculate the ratio of the initial distance to the final distance: \(R = (D1 / D2)^2\)
\(= (12 / 42)^2\)
\(= (2 / 7)^2\)
\(= 4 / 49.\)
4. Convert the initial decibel level to intensity (I1): The intensity of a sound is proportional to \(10^(L1/10).\)
\(So, I1 = 10^(100/10) = 10^10.\)
5. Calculate the final intensity (I2) using the ratio of distances: I2 = I1 * R
\(= 10^10 * (4 / 49).\)
6. Convert the final intensity back to decibels (L2): L2 = 10 * log10(I2) = \(10 * log10(10^10 * 4 / 49).\)
7. Calculate the final decibel level: L2 ≈ 10 * (10 - log10(49/4)) = 10 * (10 - 1.29)
= 87.1 decibels.
For similar question on intensity.
https://brainly.com/question/16613286
#SPJ11
Factor each polynomial.
15d -12cd^2
Answers
Answer:
3d(5-4cd)
Step-by-step explanation:
15d - 12cd² (we see that the highest common factor of 15 and 12 is 3, hence we can factor 3 out)
= 3 (5d - 4cd²) (we also notice that d appears in both terms in the parantheses. hence we can also factor d out)
= 3d(5-4cd)
The table gives the amount of money (in dollars) spent on football by a major university. Letting 2 represent the number of years since 2005, and letting y represent the amount of money spent on football, in thousands of dollars, use the regression capabilities of a graphing calculator to find the equation of the line of best fit. Round values off to the nearest hundredth. Then, use your equation to make the following predictions. Year Dollars spent on football 2005 177,000 2006 192,000 2007 207,000 2008 227.000 2009 243,000 2010 292,000 The equation of the line of best fit is: Hint Predict the amount of money that will be spent on football in the year 2022. $ s Predict the amount of money that will be spent on football in the year 2041.
Answers
The line of best-fit is of:
\(y = 21.37x + 169.58\)
Using the line:
The estimate for the spending in 2022 is of $532,870.The estimate for the spending in 2022 is of $938,900.------------------------
The line of best fit, for the amount spent on football in x years after 2005 is given by:
\(y = mx + b\)
The slope is:\(m = \frac{\sum_{i = 1}^{6} (x_i - \overline{x})(y_i - \overline{y})}{\sum_{i = 1}^{6} (x_i - \overline{x})^2}\)
We consider the means as \(\overline{x}\) and \(\overline{y}\). They are used to find the coefficient b.Also x is the number of years after 2005, thus it's measures are 0, 1, 2, 3, 4 and 5, that is, \(x_1 = 0, ..., x_5 = 5\).y is measured in thousands, thus \(y_1 = 177, ... y_6 = 292\).The means are:
\(\overline{x} = \frac{0 + 1 + 2 + 3 + 4 + 5}{6} = 2.5\)
\(\overline{y} = \frac{177 + 192 + 207 + 227 + 243 + 292}{6} = 223\)
Finding the slope:
\(\sum_{i = 1}^{6} (x_i - \overline{x})(y_i - \overline{y}) = 374\)
\({\sum_{i = 1}^{6} (x_i - \overline{x})^2} = 17.5\)
\(m = \frac{\sum_{i = 1}^{6} (x_i - \overline{x})(y_i - \overline{y})}{\sum_{i = 1}^{6} (x_i - \overline{x})^2} = \frac{374}{17.5} = 21.37\)
Now finding b:
\(y = 21.37x + b\)
Replacing the means:
\(223 = 21.37(2.5) + b\)
\(b = 169.58\)
Thus, the line of best fit is:
\(y(x) = 21.37x + 169.58\)
2022 is 2022 - 2005 = 17 years after 2005, thus, the estimate for 2022 is of:
\(y(17) = 21.37(17) + 169.58 = 532.87\)
Following the same logic, the estimate for 2041 is of:
\(y(36) = 21.37(36) + 169.58 = 938.9\)
A similar problem is given at https://brainly.com/question/16793283
Which graph matches the equation 4x² + 25y^2 = 100?

Answers
graph b matches the equation
Choose the word that correctly completes the statement. Since angle B is the largest angle, is the ________ side. adjacent included longest shortest
Answers
Since angle B is the largest angle, Line segment A C is the longest side. option C
How to complete the statementTo complete the statement, we need to know that;
Using the sine rule of a triangle, we can know that the sin value of an angle will be directly related to the length of the side it's facing.
Angle B is the largest angle out of the three. The sin value of an angle will be larger if the angle is larger (from 0 to 90). Sin 75 is 0.97, sin 60 is 0.87, and sin 45 is 0.71
That means the largest angle will have the largest sin value. The largest sin value means the side will be the longest side.
Learn more about angles at: https://brainly.com/question/25716982
#SPJ4
The complete question:
Choose the word that correctly completes the statement. Triangle A B C is shown. Angle A C B is 45 degrees, angle C B A is 75 degrees, and angle B A C is 60 degrees. Since angle B is the largest angle, Line segment A C is the ________ side.
adjacent
included
longest
shortest
Which expression is not equivalent to (5^2x)^3

Answers
Answer:
#3
Step-by-step explanation:
For this... you just multiply the exponents together to get 6x
any of the others that do NOT have 6x as a product of exponents is not equiv ..... so #3 is not equivalent
Option 3 is not equivalent to the given expression.
What is an equivalent expression?Equivalent expressions are expressions that work the same even though they look different. If two algebraic expressions are equivalent, then the two expressions have the same value when we plug in the same value for the variable.
The given expression is (5²ˣ)³.
Now, (5⁶ˣ)
(5ˣ)⁶
(5²)³ˣ
Therefore, option 3 is not equivalent to the given expression.
To learn more about an equivalent expression visit:
https://brainly.com/question/28170201.
#SPJ2
the function f(t)=570(1.55)^60t represents the change in a quantity over t minutes. what is the
rate of growth to the nearest percentage?
a. 55%
b. 5.5%
c. 45%
d 155%
Answers
The rate of growth to the nearest percentage is 55%. The result is obtained by using the exponential growth equation.
What is exponential growth equation?An exponential growth equation is an equation to express the process where the quantity increases over time. The equation of exponential growth can be expressed as
y = a × (1 + r)ˣ
Where
y = population in the expected yeara = current populationr = rate of growthx = number of periodsWe have the function: \(f(t) = 570(1.55)^{60t}\). It represents the change in a quantity over t minutes. Find the rate of growth!
Base on the exponential growth equation, we get
y = f(x)
\(a \times (1 + r)^{x} = 570(1.55)^{60t}\)
1 + r = 1.55
r = 1.55 - 1
r = 0.55
r = 55/100
r = 55%
Hence, the percentage of growth rate for the function is 55%.
Learn more about exponential growth equation here:
brainly.com/question/30134905
#SPJ4
x/7 ≥ − 6=============
Answers
The range of value of x in the inequality x/7 ≥ -6 is x≥ -42
What is inequality?Inequality, is a statement of an order relationship. Some terms used in inequality are ,greater than, greater than or equal to, less than, or less than or equal to. They are used between two numbers or algebraic expressions.
greater than has the sign >
greater than or equal to has the sign ≥
less than has the sign < and
less than or equal to has ≤
solving the range of value of x in the inequality x/7 ≥- 6
multiply both sides by 7
x ≥ -42
Therefore the range of value of x is x ≥ -42
learn more about inequality from
https://brainly.com/question/24372553
#SPJ1
A [?] degrees
43°
15° C
B
С
What is the measure of ZA?
Enter
![A [?] degrees4315 CBWhat is the measure of ZA?Enter](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/ZAZzRGlns6hGhRsYJN97sefcvCzvzecT.png)
Answers
Answer:
A=122
Step-by-step explanation:
The sum of degree of angles in a triangle=180
Angle a =180-43-15=122
What is the value of (ΣX)2 for the scores 1, 5, 2?(PLEASE EXPLAIN)10163064
Answers
The value of (ΣX)² for the scores 1, 5, 2 is:
64
What is a summation?
It is the representation of the sum of infinite or many values. And it is represented by the following symbol:
∑xi
The value of (ΣX)² for the scores 1, 5, 2 can be found by first finding the summation of the scores and then squaring the result.
Steps to follow:
Step 1: Find the summation of the scores.
ΣX = 1 + 5 + 2 = 8
Step 2: Square the summation.
(ΣX)² = 82 = 64
Therefore, the value of (ΣX)² for the scores 1, 5, 2 is 64.
More information about summation here:
https://brainly.com/question/11741791
#SPJ11
Determine the minimum rotation (in degrees) which will carry the following figure onto itself ( where all sides and verticles will match up). Round to the nearest tenth if necessary.
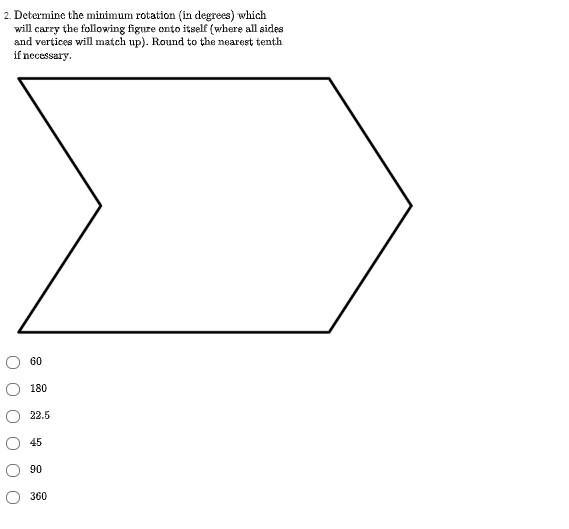
Answers
Answer:
360°
Step-by-step explanation:
The figure is irregular which means it must be completely rotated to have matching sides and vertices. A full rotation is equal to 360°.
Two towns are located at points A(2,-2) and B (8,5). A new school is to be built on a straight road with equation -x+7y=-4. Find the location of the school so that it is equaidistant from the two towns
Answers
Answer: The location is (8.88, -1.84)
Step-by-step explanation:
We know that the school is on the line:
x + 7*y = -4
or we can rewrite this as:
x = -4 - 7*y
Then, the points on this line can be written as:
(-4 - 7*y, y).
Then we can assume that the school is located at the point:
(-4 - 7*a, a)
and we need to find the value of a.
Now, we have two towns in the points:
A = (2, - 2)
B = (8, 5)
The distance between two points (a, b) and (c, d) is:
D = √( (a- c)^2 + (b - d)^2)
And we want that the school to be equidistant between the two cities, then if the distance to the citie A is:
Da = √( (2 + 4 + 7*a)^2 + (-2 - a)^2)
And the distance to the city B is:
Db = √( (8 + 4 + 7*a)^2 + (5 - a)^2)
Then we must have that:
Da = Db
√( (2 + 4 + 7*a)^2 + (-2 - a)^2) = √( (8 + 4 + 7*a)^2 + (5 - a)^2)
then:
(2 + 4 + 7*a)^2 + (-2 - a)^2 = (8 + 4 + 7*a)^2 + (5 - a)^2
Let's solve this for a.
(6 + 7*a)^2 + (-2 - a)^2 = (12 + 7*a)^2 + (5 - a)^2
36 + 84*a + 49*a^2 + 4 + 4*a + a^2 = 144 + 168*a + 49*a^2 + 25 - 10*a + a^2
let's simplify this:
36 + 84*a + 4 + 4*a = 144 + 168*a + 25 - 10*a
-129 = 70*a
-129/70 = a = -1.84
Then the location of the school is:
y = -1.84
x = -4 - 7*-1.84 = 8.88
(8.88, -1.84)
a hospital claims that the mean wait time for emergency room patients is more than 38 minutes. identify the null hypothesis, h0, and the alternative hypothesis, ha, in terms of the parameter μ.
Answers
Null hypothesis (H0): The mean wait time for emergency room patients is equal to or less than 38 minutes (H0: μ ≤ 38).
Alternative hypothesis (Ha): The mean wait time for emergency room patients is more than 38 minutes (Ha: μ > 38).
The null hypothesis, denoted as H0, is a statement that assumes there is no significant difference or relationship between variables in a statistical analysis. In this case, the null hypothesis is that the mean wait time for emergency room patients is equal to or less than 38 minutes, represented as H0: μ ≤ 38.
On the other hand, the alternative hypothesis, denoted as Ha or H1, is a statement that contradicts or opposes the null hypothesis. It suggests that there is a significant difference or relationship between variables. In this scenario, the alternative hypothesis is that the mean wait time for emergency room patients is more than 38 minutes, represented as Ha: μ > 38.
To summarize:
- Null hypothesis (H0): The mean wait time for emergency room patients is equal to or less than 38 minutes (H0: μ ≤ 38).
- Alternative hypothesis (Ha): The mean wait time for emergency room patients is more than 38 minutes (Ha: μ > 38).
In hypothesis testing, we collect data to determine whether there is enough evidence to reject the null hypothesis in favor of the alternative hypothesis.
Learn more about null hypothesis :
https://brainly.com/question/28920252
#SPJ11
NEED HELP ASAP!!! WILL MARK BRAINLIEST!!!
Write an equation (a) in slope-intercept form and (b) in standard form for the line passing through (-1,5) and parallel to x+3y=7.
Answers
Answer:x + 3y = 5
3y = -x + 5
y = -(1/3)x + 5/3
slope = -1/3 Parallel lines have the same slope.
Now, you have a point and a slope, so use the Point-Slope form of the equation of a line.
y - y1 = m(x - x1)
y - 4 = (-1/3)(x + 2)
y - 4 = (-1/3)x - 2/3
y = (-1/3)x + 3 1/3 Slope-intercept Form
(1/3)x + y = 10/3 Multiply both sides by 3.
x + 3y = 10 Standard form
Hope this helps and don't yell at me in the comments if I am wrong
plz mark me brainliest if I am correct
Answer:
The correct answer is y= -x/3 + 14/3 and x + 3y = 14.
Decide if the segments can make a triangle. Answer with Yes/No and explain your answer.
9: 8 cm, 12 cm, 16 cm
10: 5 in, 7 in, 20 in
Answers
9. Yes, since \(8+12>16\), meaning the side lengths satisfy the triangle inequality.
10. No, since \(5+7<20\), meaning the side lengths do not satisfy the triangle inequality.
Dr. Fahrrad has been riding his bike to his job and is curious how many ATP his body is breaking apart in order to do the work required to get to his job.
Dr. Fahrrad rides 4.6 kilometers to his job, has a mass of 74.9 kilograms and has an average acceleration of 1.4 kilometers per second squared.
The molecule ATP is able to do work, measured in kilojoules per mole of ATP broken into ADP. The SI unit for work is a joule. Using the information given we can calculate work and then convert to moles of ATP.
The first step is to take stock of what we are given in the word problem and what we are trying to find. We have mass, distance, and average acceleration. We are trying to find how many ATP are required to power the bike ride to work.
The equation for work, is force times distance and will tell us how many joules Dr. Farrhad is using on his bike ride. It also incorporates one of our given variables, distance. However, the distance was reported in kilometers and the SI unit of distance is the meter. It is necessary to convert to meters before using this equation.
The equation for Force is mass times acceleration. This will incorporate our remaining two variables, mass and acceleration. Again, the information given to us was in km·s-2 but the SI unit for acceleration is m·s-2. It is necessary to convert to m·s-2 before substituting into the equation.
By substituting the equation for F into the equation for W, we can figure out how many joules Dr. Fahrrad is burning on his ride to his job.
In order to use these equations, we are assuming quite a few things. Below are some of the assumptions.
no friction
no mass of the bike
a flat ride with no change in altitude
This equation above will calculate work in joules. The conversion factor for switching between ATP and work is given in kilojoules. The units must match to correctly perform the conversion.
The last step is to convert work, calculated in joules, into moles of ATP being broken required to do the work. If we assume standard temperature and pressure, the breakdown of a mole of ATP releases 29 kilojoules available to do work.
How many moles of ATP is Dr. Farrhad breakdown to get to work? Report your answer to one decimal place.
Answers
Dr. Fahrrad breaks down 0.23 moles of ATP to get to work.
The first step is to calculate the work done by Dr. Fahrrad on his bike ride. We can use the following equation:
W = F * d
where:
W is the work done in joules
F is the force in newtons
d is the distance in meters
The force is equal to the mass of Dr. Fahrrad times his acceleration. We can convert the acceleration from kilometers per second squared to meters per second squared by multiplying by 1000/3600. This gives us a force of 102.8 newtons.
The distance of Dr. Fahrrad's bike ride is 4.6 kilometers, which is equal to 4600 meters.
Plugging these values into the equation for work, we get:
W = 102.8 N * 4600 m = 472320 J
The breakdown of a mole of ATP releases 29 kilojoules of energy. So, the number of moles of ATP that Dr. Fahrrad breaks down is:
472320 J / 29 kJ/mol = 162.6 mol
To one decimal place, this is 0.23 moles of ATP.
Here are the assumptions that we made in this calculation:
No friction
No mass of the bike
A flat ride with no change in altitude
These assumptions are not always realistic, but they are a good starting point for this calculation. In reality, Dr. Fahrrad would probably break down slightly more than 0.23 moles of ATP to get to work.
Learn more about squared here: brainly.com/question/14198272
#SPJ11
since the mode is the most frequently occurring data value, it group of answer choices is always larger than the mean can never be larger than the mean none of these alternatives is correct. is always larger than the median
Answers
Since the mode is the most frequently occurring data value so -
Option D : None of the alternatives is correct.
What is mode?
A mode is described as the value in a group of values that occurs more frequently. The value that appears the most frequently is called mode.
The distribution of the mean, median, and mode values will depend on how skewed the distribution is.
The total dependency of mean, median and mode of data is on the asymmetric form of the data.
As a result, mean or mode may be larger than or less than mode.
Therefore, the mode is neither large than mean or median and can never be larger than mean.
To learn more about mode from the given link
https://brainly.com/question/14532771
#SPJ1
if you wanted to compute the correlation between two ordinal-level variables, which type of correlation should you use?
Answers
To compute the correlation between two ordinal-level variables, you should use Spearman's rank correlation coefficient.
What is Spearman's rank correlation coefficient?Spearman's rank correlation coefficient is a non-parametric statistical measure that is used to assess the association between two ordinal-level (ordinal or ranked) variables.
This type of correlation calculates the correlation between the ranks of the data rather than the actual values, making it suitable for ordinal data where the difference between the levels is not well defined.
The coefficient ranges from -1 to 1, where a value of 1 indicates a perfect positive correlation, a value of -1 indicates a perfect negative correlation, and a value of 0 indicates no correlation.
Learn more about Spearman's rank correlation coefficient at:
https://brainly.com/question/14646555
#SPJ1
at the town flea market, monica purchases a big box of used tennis balls to throw to her dog. she scoops some tennis balls out of the box at random. here are the colors of the balls: yellow, blue, yellow, red, green, blue, yellow, red, yellow, green, yellow, red, green based on the data, what is the probability of choosing a yellow tennis ball from the box? write your answer as a fraction or whole number. submit
Answers
Answer: 5/13
Step-by-step explanation: i did this IXL and got it right
find a value of c> 1 so that the average value of f(x)=(9pi/x^2)cos(pi/x) on the interval [2, 20]
Answers
c = pi/2, and the value of c > 1 such that the average value of f(x) on the interval [2, 20] is equal to c is c = pi/2.
The average value of a function f(x) on the interval [a, b] is given by:
Avg = 1/(b-a) * ∫[a, b] f(x) dx
We want to find a value of c > 1 such that the average value of the function \(f(x) = (9pi/x^2)cos(pi/x)\) on the interval [2, 20] is equal to c.
First, we find the integral of f(x) on the interval [2, 20]:
\(∫[2, 20] (9pi/x^2)cos(pi/x) dx\)
We can use u-substitution with u = pi/x, which gives us:
-9pi * ∫[pi/20, pi/2] cos(u) du
Evaluating this integral gives us:
\(-9pi * sin(u) |_pi/20^pi/2 = 9pi\)
Therefore, the average value of f(x) on the interval [2, 20] is:
\(Avg = 1/(20-2) * ∫[2, 20] (9pi/x^2)cos(pi/x) dx\)
= 1/18 * 9pi
= pi/2
Now we set c = pi/2 and solve for x:
Avg = c
\(pi/2 = 1/(20-2) * ∫[2, 20] (9pi/x^2)cos(pi/x) dx\)
pi/2 = 1/18 * 9pi
pi/2 = pi/2
Therefore, c = pi/2, and the value of c > 1 such that the average value of f(x) on the interval [2, 20] is equal to c is c = pi/2.
To know more about function refer to-
https://brainly.com/question/12431044
#SPJ11
A sequence is represented by the explicit formula and A sequence is represented by the recursive formula below:
What is the sequence represented by the formula? please help with these two questions it for a test


Answers
Answer:
Answer:
Option C is correct.
Explanation:
Explicit formula for the geometric sequence is given by:
where r is the common ratio term.
Given the recursive formula for geometric sequence:
For n =2
⇒
For n =3
⇒
Common ratio(r):
and so on..
⇒ r = 3
Therefore, the explicit formula for the geometric sequence represented by the recursive formula is:
Step-by-step explanation:
An independent set in a graph is a set of vertices S⊆V that contains no edge (so no pair of neighboring vertices is included). The max independent set problem is to find an independent set of maximum size in a graph G. (a) Write the max independent set problem as an integer linear program. (b) Write an LP relaxation for the max independent set problem. (c) Construct an example (a family of graphs) to show that the ratio LP-OPT / OPT can be at least cn where c>0 is some absolute constant and n is the number of vertices of the graph. (d) What is the (exact) relation between the size of a max independent set and the size of min vertex cover of a graph? (e) Using this relation, what does the 2-approximation algorithm for vertex cover imply for an approximation algorithm for max independent set?
Answers
The independent set in a graph is a set of vertices that contain no edges. So, no neighboring vertices are included. The max independent set problem is to get an independent set of maximum size in graph G.
The solution for this question is discussed below:
a) The integer linear program for the max independent set problem is as follows:
maximize ∑x_i Subject to: x_i+x_j ≤ 1 {i,j} ∈ E;x_i ∈ {0, 1} ∀i. The variable x_i can represent whether the ith vertex is in the independent set. It can take on two values, either 0 or 1.
b) The LP relaxation for the max independent set problem is as follows:
Maximize ∑x_iSubject to:
xi+xj ≤ 1 ∀ {i, j} ∈ E;xi ≥ 0 ∀i. The variable xi can take on fractional values in the LP relaxation.
c) The family of graphs is as follows:
Consider a family of graphs G = (V, E) defined as follows. The vertex set V has n = 2^k vertices, where k is a positive integer. The set of edges E is defined as {uv:u, v ∈ {0, 1}^k and u≠v and u, v differ in precisely one coordinate}. It can be shown that the size of the max independent set is n/2. Using LP, the value can be determined. LP provides a value of approximately n/4. Therefore, the ratio LP-OPT/OPT is at least c/4. Therefore, the ratio is in for a constant c>0.
d) The size of a max-independent set is equivalent to the number of vertices minus the minimum vertex cover size.
e) The 2-approximation algorithm for vertex cover implies a 2-approximation algorithm for the max independent set.
To know more about the independent set, visit:
brainly.com/question/31418821
#SPJ11
3. The Similar Triangle Method (9 points total)
To prove that the Pythagorean theorem works, leave out the dimensions and represent the trunk of the
car with a right triangle ABC.
Drawing an altitude from vertex C to side c creates two new triangles, BCD and ACD (see diagram).
B
C
1
a. Here are the three triangles shown separately These triangles are similar. How do you know? HINT:
Compare the angle measures. (1 point)

Answers
The triangles BCD, ACD, and ABC are similar because their corresponding angles are congruent. This similarity allows us to apply the Pythagorean theorem to establish the relationship between the sides of the right triangle, proving its validity.
To prove that triangles BCD, ACD, and ABC are similar, we need to compare their angle measures. Let's analyze the angles in each triangle:
Triangle ABC:
- Angle BAC: This is a right angle as it represents the right angle of the right triangle.
Triangle BCD:
- Angle BCD: This angle is also a right angle as the altitude from vertex C forms a perpendicular line with side BC.
- Angle CBD: This angle is congruent to angle BAC in triangle ABC. Both angles are corresponding angles and are congruent due to the definition of perpendicular lines.
Triangle ACD:
- Angle ACD: This angle is a right angle, formed by the altitude from vertex C intersecting side AD.
- Angle CAD: This angle is congruent to angle BAC in triangle ABC. They are corresponding angles and are congruent due to the definition of perpendicular lines.
Based on the analysis of the angles, we can conclude that triangles BCD and ACD are both right triangles and have congruent angles to triangle ABC. Therefore, by the Angle-Angle (AA) similarity postulate, we can say that triangles BCD and ACD are similar to triangle ABC.
The similarity of these triangles implies that their corresponding sides are proportional. In this case, we have the following corresponding sides:
BC : AC = BD : AD = CD : CD (which is equal to 1)
The proportionality of these sides allows us to apply the Pythagorean theorem to any of the triangles.
By the Pythagorean theorem, in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. In triangle ABC, we have:
\(AB^2 + BC^2 = AC^2\)
Since triangles BCD and ACD are similar to triangle ABC, we can use the same equation to represent the sides of these triangles:
\(BD^2 + CD^2 = BC^2\)
\(AD^2 + CD^2 = AC^2\)
Therefore, by proving the similarity of triangles BCD and ACD to triangle ABC, we have established the validity of the Pythagorean theorem within the context of the given right triangle ABC.
In conclusion, the three triangles BCD, ACD, and ABC are similar, and this similarity allows us to apply the Pythagorean theorem to establish the relationship between the sides of the right triangle. This proof demonstrates the validity of the Pythagorean theorem in the context of the given triangle.
For more such information on: triangles
https://brainly.com/question/28600396
#SPJ8

use trigonometry to find the unknown side (round to 1 decimal)

Answers
Answer:
a = 7.5
Step-by-step explanation:
Using the sine ratio in the right triangle and the exact value
sin30° = \(\frac{1}{2}\) , then
sin30° = \(\frac{opposite}{hypotenuse}\) = \(\frac{a}{15}\) = \(\frac{1}{2}\) ( cross- multiply )
2a = 15 ( divide both sides by 2 )
a = 7.5