whats 255x67777675456745675676745
Answers
Answer: 1.728330724e+25 thats what it said when I calcuated it.
Related Questions
What is another way to describe the following expression?
5 - (x + y)
A. the difference of 5 and the cube of the sum of x and y
B. the product of 5 and the sum of x and y
C. the product of 5 and the cube of the sum of x and y
D. the difference of 5 and the sum of x and y

Answers
A. The difference of 5 and the cube of the sum of x and y
I’m struggling help ASAP

Answers
Answer:
see explanation
Step-by-step explanation:
The n th term of an arithmetic sequence is
\(a_{n}\) = a₁ + (n - 1)d
where a₁ is the first term and d the common difference
Here a₁ = 40 ( first row )
d = - 4 ( 4 fewer than the row below ), thus
\(a_{n}\) = 40 - 4(n - 1) = 40 - 4n + 4 = 44 - 4n
That is
\(a_{n}\) = 44 - 4n
(b)
a₁₀ = 44 - 4(10) = 44 - 40 = 4
There are 4 boxes on the 10 th row
Formulate and solve the following linear program: You are trying to create a budget to optimize the use of a portion of your disposable income. You have a maximum of $1,500 per month to be allocated to food, shelter, and entertainment. The amount spent on food and shelter combined must not exceed $1,100. The amount spent on shelter alone must not exceed $800. Entertainment cannot exceed $400 per month. Each dollar spent on food has a satisfaction value of 2, each dollar spent on shelter has a satisfaction value of 3, and each dollar spent on entertainment has a satisfaction value of 5. 1. Write the Objective Function and Constraints for this problem. 2. Assuming a linear relationship, use the Excel Solver to determine the optimal allocation of your funds. 3. Report the maximum value of the Objective function.
Answers
1. Objective Function and Constraints:
Maximize 2x1 + 3x2 + 5x3 subject to x1 + x2 + x3 ≤ 1500, x1 + x2 ≤ 1100, x2 ≤ 800, x3 ≤ 400.
2. Using Excel Solver, find the optimal allocation of funds.
3. The maximum value of the objective function is reported by Excel Solver.
We have,
Objective Function and Constraints:
Let:
x1 = amount spent on food
x2 = amount spent on shelter
x3 = amount spent on entertainment
Objective Function:
Maximize: 2x1 + 3x2 + 5x3 (since each dollar spent on food has a satisfaction value of 2, each dollar spent on shelter has a satisfaction value of 3, and each dollar spent on entertainment has a satisfaction value of 5)
Constraints:
Subject to:
x1 + x2 + x3 ≤ $1,500 (maximum disposable income)
x1 + x2 ≤ $1,100 (amount spent on food and shelter combined must not exceed $1,100)
x2 ≤ $800 (amount spent on shelter alone must not exceed $800)
x3 ≤ $400 (entertainment cannot exceed $400)
Using Excel Solver:
In Excel, set up a spreadsheet with the following columns:
Column A: Variable names (x1, x2, x3)
Column B: Objective function coefficients (2, 3, 5)
Column C: Constraints coefficients (1, 1, 1) for the first constraint (maximum disposable income)
Column D: Constraints coefficients (1, 1, 0) for the second constraint (amount spent on food and shelter combined)
Column E: Constraints coefficients (0, 1, 0) for the third constraint (amount spent on shelter alone)
Column F: Constraints coefficients (0, 0, 1) for the fourth constraint (entertainment limit)
Column G: Right-hand side values ($1,500, $1,100, $800, $400)
Apply the Excel Solver tool with the objective function and constraints to find the optimal allocation of funds.
Once the Excel Solver completes, it will report the maximum value of the objective function, which represents the optimal satisfaction value achieved within the given budget constraints.
Thus,
Objective Function and Constraints: Maximize 2x1 + 3x2 + 5x3 subject to x1 + x2 + x3 ≤ 1500, x1 + x2 ≤ 1100, x2 ≤ 800, x3 ≤ 400.
Using Excel Solver, find the optimal allocation of funds.
The maximum value of the objective function is reported by Excel Solver.
Learn more about Objective Functions and Constraints here:
https://brainly.com/question/28987013
#SPJ4
Nathan took his car in for service and repairs. He had a coupon for 10% off
Which amount is closest to Nathan‘s total cost after the 10% discount and including 6% sales tax? [Assume text is applied after the discount is applied.]

Answers
Answer:
C. $571.
Step-by-step explanation:
1st you have to add up the total cost so:
213.15 + 344.21 + 76.65 = $ 634.01
next find 10% of 634.01
10% of 634.01 is 63.401
then you subtract 63.401 from 634.01 so basically you subtract the 10% discount from the total cost so:
634.01 - 63.401 = 570.609 is equal to $576.90
$576.90 is closest to $571
Hope this helps : )
$10 bet between you and me. At any time during the game, I can ask to double it. If you accept we both put in another $10 and if you win, you win the $20 and if you lose, you lose it all. If you reject, you lose the initial $10. What is the minimum probability you would take to accept the double
Answers
Answer:
66%
Step-by-step explanation:
\(-10x\:+\:\left(20\cdot \left(1-x\right)\right)=\:0\)
x = \(\frac{2}{3}\) = .666 = 66%
directions: use the digarm to find the correct symbol. Start at the start box and work through the made until you get to the finish box

Answers
To solve this problem, we just need to look for the paths that match each box.
The path from start to finish box is shown by the image below.
As you can observe in the image above, the first connection is on the left of the start box because it matches the segment BD inside the box.
Then, we go to the left again because the second box contains the ray DB.
After, we go through the line BD and choose the path that matches.
We keep using the same logic until we get to the finish box.

A cell phone company sells about 500 phones each week when it charges $75 per phone. It sells about 20 more phones per week for each$1 decrease in price. The company's revenue is the product of the number of phones sold and the price of each phone. What price should the company charge to maximize its revenue?
Answers
The company can maximize its revenue by charging the price of $73 per phone.
Changing the price and monitoring how many phones are sold in reaction to the price change allows for trial-and-error in determining accuracy.
With 520 phones sold each week at $73, the corporation will make a total of $38,160 in revenue. There are 20 more phones than when it was charging $75, thus the business will make an additional $1,500 every week.
Due to the increased number of phones sold, the corporation may increase revenue by merely $2 by lowering the price, leading to an increase in both total revenue and profit.
To learn more about revenue visit:
https://brainly.com/question/31336205
#SPJ4
Which congruence theorem can be used to prove △WXZ ≅ △YZX? Triangles W X Z and Y Z X share side X Z. Angles W X Z and X Z Y are right angles. Angles X W Z and X Y Z are congruent. AAS ASA SAS HL
Answers
Answer:
The correct option is AAS.
Step-by-step explanation:
Consider the diagram below.
It is provided that The triangles △ WXZ and △ YZX share a side XZ.Angles ∠WXZ and ∠XZY are right angles.Angles ∠XWZ and ∠XYZ are congruent.If two angles are congruent it implies that they are same in degrees or radians.
So, the angles ∠XWZ and ∠XYZ are equal.
So, in the diagram below, one of the triangles have two angles that are equal to the corresponding angles on the other triangle and the two triangles share a side.
Then according to the Angle-Angle-Side (AAS) statement the triangles △ WXZ and △ YZX are congruent.
Thus, the correct option is AAS.

The congruence theorem that can be used to prove that △WXZ ≅ △YZX is; AAS
We are told that;ΔWXZ and ΔYZX share side XZ
∠WXZ and ∠XZY are right angles
∠XWZ and ∠XYZ are congruent
Now, from the given parameters, we can say that from reflexive property of congruence, XZ is congruent to itself and thus, we have one side of both triangles that is congruent.Secondly, since ∠WXZ and ∠XZY are right angles, it means they are equal and therefore congruent to each other.Lastly, we are told that ∠XWZ and ∠XYZ are congruent.In summary, we have 2 corresponding angles and one corresponding side that are equal but the corresponding side is not with the included angles and as such the triangles are congruent by AAS Congruency.Read more about AAS Congruency at; https://brainly.com/question/7727792
1) -8 + |-6|
Find the value of the following
Answers
Answer:
-2
Step-by-step explanation:
-8 + |-6|
|-6| = 6
so you put 6 instead of |-6|
-8 + 6 which equals -2.
:D
find minimum number of coins that make a given value
Answers
The given coins [1, 2, 5] and the value 11, the minimum number of coins needed is 2.
Here are the steps to find the minimum number of coins:
1. First, we create an array of size equal to the given value, initialized with a very large number. This array will store the minimum number of coins needed to make each value from 0 to the given value.
2. We set the first element of the array to 0, as it doesn't require any coins to make a value of 0.
3. Next, we iterate through all the coins available and for each coin, we iterate through all the values from the coin value to the given value.
4. For each value, we calculate the minimum number of coins needed by taking the minimum of the current minimum and the value obtained by subtracting the coin value from the current value and adding 1 to it.
5. Finally, we return the value stored in the last element of the array, which represents the minimum number of coins needed to make the given value.
Let's consider an example to better understand the process:
Given coins: [1, 2, 5]
Given value: 11
1. Initialize the array with [INF, INF, INF, INF, INF, INF, INF, INF, INF, INF, INF, INF] (INF represents infinity).
2. Set the first element of the array to 0, so it becomes [0, INF, INF, INF, INF, INF, INF, INF, INF, INF, INF, INF].
3. For the first coin (1), iterate through the array from index 1 to 11.
- For index 1, the minimum number of coins needed is 0 + 1 = 1.
- For index 2, the minimum number of coins needed is 0 + 1 = 1.
- For index 3, the minimum number of coins needed is 0 + 1 = 1.
- ...
- For index 11, the minimum number of coins needed is 0 + 1 = 1.
The array becomes [0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1].
4. For the second coin (2), iterate through the array from index 2 to 11.
- For index 2, the minimum number of coins needed is 1 (minimum of 1 and 0 + 1 = 1).
- For index 3, the minimum number of coins needed is 1 (minimum of 1 and 0 + 1 = 1).
- For index 4, the minimum number of coins needed is 1 (minimum of 1 and 1 + 1 = 2).
- ...
- For index 11, the minimum number of coins needed is 1 (minimum of 1 and 1 + 1 = 2).
The array becomes [0, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2].
5. For the third coin (5), iterate through the array from index 5 to 11.
- For index 5, the minimum number of coins needed is 2 (minimum of 2 and 0 + 1 = 1).
- For index 6, the minimum number of coins needed is 2 (minimum of 2 and 1 + 1 = 2).
- ...
- For index 11, the minimum number of coins needed is 2 (minimum of 2 and 2 + 1 = 3).
The array becomes [0, 1, 1, 1, 2, 1, 2, 2, 2, 2, 3, 2].
6. The minimum number of coins needed to make the given value (11) is 2.
To know more about coins here:
brainly.com/question/32385642
#SPJ11
-78 = -5a = 7
solve for a lol
Answers
87 i think Step-by-step explanation:
A particular lane has a flow rate of 1800 vph. Approximately how many gaps will there be in one hour that are longer than 6 seconds
Answers
An approximate of 4 gaps will be there in one hour that are longer than 6 seconds at the flow rate of 1800 vph.
The flow rate is given to be 1800 vph.
This means that 1800 vehicles pass through the lane every hour.
To determine the number of gaps that are longer than 6 seconds, we need to calculate the time it takes for one vehicle to pass and then subtract it from 60 minutes.
Assuming that the vehicle length is negligible, the gap between two consecutive vehicles is equal to the time taken by one vehicle to pass by completely plus the time taken by the following vehicle to reach the starting position of the preceding vehicle.
Let's say, for example, that the time it takes for one vehicle to pass is 2 seconds.
The gap between two consecutive vehicles would then be 2 + 2 = 4 seconds, meaning that there would be 60/4 = 15 gaps in one minute, or 900 gaps in one hour.
If we assume that the time it takes for one vehicle to pass is 2 seconds, the total time taken for a vehicle to cover the distance would be 1/1800*60*60= 2 sec.
Hence, 60/2 = 30 vehicles would pass through the lane in one minute.1800 vehicles/60 minutes = 30 vehicles/min
Now, we know that the gap between two consecutive vehicles is 2 seconds, so we can calculate the number of vehicles that pass through the lane in one minute.
30 vehicles/min x 2 sec/vehicle = 60 seconds/min
We can see that there are 60 seconds in a minute.
Thus, the total time taken for a vehicle to pass is 60/1800 = 0.033 minutes.
So, the total number of gaps that are longer than 6 seconds would be:
Number of minutes in an hour = 60.
Number of vehicles that pass through the lane in an hour = 1800.
Time taken for one vehicle to pass = 0.033 minutes.
Therefore, number of gaps = 60 - (1800 x 0.033) / 6 = 4 gaps.
An approximate of 4 gaps will be there in one hour that are longer than 6 seconds.
Learn more about flowrate here:
https://brainly.com/question/14291335
#SPJ11
parallelogram ABCD is shown with diagnols, line AC and DB intersecting at point E. If AE = 4x - 3 and EC = 3x - 1, what is the length of line AC?
Answers
Answer:
10
Step-by-step explanation:
So because AC is intersected at the middle, or the midpoint, being E, you can say that both sides of AC; AE and EC, are equal to each other. You can make 4x-3=3x-1 and combine like terms to get X on one side by itself. First, you want to subtract 3x from both sides to move the x from left side and only have it on the right. You should x-3=-1. Then, you want to remove the -3 from the left side and bring it to the right to have x by itself. To cancel the -3 on the left side you have to add 3 on both sides. You should have x=2. Now that you have x, you can plug it into both AE and EC, then add them together. You should have 5 for AE and 5 for EC, and adding them up makes 10. Hope I could help :)

how much 500 grams to pounds?
Answers
500 grams is approximately equal to 1.1023 pounds ( rounded to four decimal places )
The conversion factor to convert grams to pounds is 0.00220462
1 gram = 0.00220462 pounds
The conversion is the process of changing the unit of one quantity to another units
The conversion factor is defined as the number that is used to change one unit to another units by multiplying or dividing
The mass in pounds = The mass in grams × conversion factor
Substitute the values in the equation
1 gram = 0.00220462 pounds
500 grams = 500 × 0.00220462
Multiply the numbers
= 1.1023 pounds ( rounded to four decimal places )
Therefore, 250 grams is 0.5511 pounds
Learn more about conversion factor here
brainly.com/question/23718955
#SPJ4
CATNUMATICAL Reason Quantitatively Rachel, Timothy, and Robyn each make
the rectangular prism shown. If they stand all of their prisms together, side by
side, to make one large rectangular prism, what is the volume of the new prism?
How did the dimensions change?
HELP!!!!!!!
Answers
Answer:
See explanation
Step-by-step explanation:
The question is incomplete, as the dimension of each prism is not given.
So, I will give a general explanation.
From the question, we understand each prism.
So, to get the new volume; we simply add up the volume of each prism.
For instance (we want to make assumptions)
Rachel
\(Length = 4; Width = 3; Height = 4\)
Timothy
\(Length = 6; Width = 3; Height = 4\)
Robyn
\(Length = 4; Width = 8; Height = 3\)
So, we have:
\(Volume = Length * Width * Height\)
For each, we have:
\(Rachel =4* 3* 4 =48\)
\(Timothy= 6* 3* 4 = 72\)
\(Robyn = 4* 8* 3 = 96\)
The volume of the new
\(Volume = 48 + 72 + 96\)
\(Volume = 216\)
The dimension of new prism.
Using the assumed values, we have:
\(Length = 4; Width = 3; Height = 4\)
\(Length = 6; Width = 3; Height = 4\)
\(Length = 4; Width = 8; Height = 3\)
Now, we consider the measure of the sides
Sides with the same length will form a new side.
Side 1
\(Length =4\) --- Rachel
\(Height = 4\) ---- Timothy
\(Length = 4\) --- Robyn
The above lengths have the same measure. So, one of the sides of the new prism will assume the value of this length.
So:
\(Length = 4\) -- for the new prism
Side 2
\(Width =3\)
\(Width = 3\)
\(Height = 3\)
The above lengths have the same measure. So, one of the sides of the new prism will assume the value of this length.
So:
\(Width = 3\) -- for the new prism
Side 2
\(Height = 4\)
\(Length = 6\)
\(Width =8\)
For this, we simply add up each length.
So, we have:
\(Height = 4 + 6 + 8\)
\(Height = 18\) --- for the new prism
So, the new dimension is:
\(Length = 4\)
\(Length = 6\)
\(Height = 18\)
\(Volume = 4 * 3 * 18\)
\(Volume = 216\)
What is the sum of 7 of the interior angles of a regular decagon?
Answers
Answer:1440 degrees
Step-by-step explanation:
The interior angles of a decagon is 1440 degrees. All sides are the same length (congruent) and all interior angles are the same size.
Find a parametrization of the portion of the plane x + y + z = 3 that is contained inside the following a. Inside the cylinder x² + y2 b. Inside the cylinder y2 + z = 4 a. What is the correct parameterization?
Answers
Apologies for the previous confusion. Let's reconsider the problem to find the correct parameterization.
a. Inside the cylinder x^2 + y^2:
To find a parametrization of the portion of the plane x + y + z = 3 that is inside the cylinder x^2 + y^2, we can use cylindrical coordinates.
In cylindrical coordinates, we have:
x = ρ*cos(θ)
y = ρ*sin(θ)
z = 3 - ρ*cos(θ) - ρ*sin(θ)
Using the equation of the plane x + y + z = 3, we can substitute these expressions to obtain:
ρ*cos(θ) + ρ*sin(θ) + (3 - ρ*cos(θ) - ρ*sin(θ)) = 3
Simplifying, we find:
ρ*cos(θ) + ρ*sin(θ) = 3
Therefore, the correct parameterization for the portion of the plane x + y + z = 3 that is contained inside the cylinder x^2 + y^2 is:
x = ρ*cos(θ)
y = ρ*sin(θ)
z = 3 - ρ*cos(θ) - ρ*sin(θ)
b. Inside the cylinder y^2 + z = 4:
To find a parametrization of the portion of the plane x + y + z = 3 that is inside the cylinder y^2 + z = 4, we can use cylindrical coordinates.
In cylindrical coordinates, we have:
x = x (remains unchanged)
y = ρ*sin(θ)
z = 4 - ρ^2
Therefore, the correct parameterization for the portion of the plane x + y + z = 3 that is contained inside the cylinder y^2 + z = 4 is:
x = x (remains unchanged)
y = ρ*sin(θ)
z = 4 - ρ^2
To know more about plane visit-
brainly.com/question/32544300
#SPJ11
(11x + 2) + (9x − 4)
MARKING BRAINLIST IF YOU CORRECTLY ANSWER
Answers
Answer:
20x-2
Step-by-step explanation:
Eliminate redundant parentheses:
(11+2)+(9−4)
11+2+9−4
Subtract the numbers:
11+2+9−4
11−2+9
Combine like Terms:
11−2+9
20−2
Solution:
20x-2
Find h(x) if h′(x)=5x/(7−x^2)^(5/3) and h(1)=−7
Answers
The function h(x) can be found by integrating h'(x) with respect to x. Using the given initial condition h(1) = -7, we get\(h(x) = -15/2 * (7 - x^2)^{(-2/3)} + (-7 + 15/2 * 6^{(-2/3)}).\)
To find h(x), we integrate h'(x) with respect to x. The given derivative\(h'(x) = 5x/(7-x^2)^{(5/3)\)can be simplified by factoring out x in the numerator:
\(h'(x) = 5x/(7-x^2)^{(5/3) }= 5x/((7-x)(7+x))^{(5/3)}.\)
Now, we can use the substitution u = 7 - x^2 to simplify the expression further. Taking the derivative of u with respect to x, we have du/dx = -2x, which implies dx = -du/(2x).
Substituting these values into the integral, we have:
∫h'(x) dx = ∫\(5x/((7-x)(7+x))^{(5/3)} dx\)
= ∫\((5x/u^{(5/3)}) (-du/(2x))\)
= ∫\((-5/u^{(5/3)})\) du.
Simplifying the expression inside the integral, we obtain:
h(x) = -5∫\(u^{(-5/3) }du\)
Integrating \(u^{(-5/3)\) with respect to u, we add 1 to the exponent and divide by the new exponent:
\(h(x) = -5 * (u^{(-5/3 + 1)}/(-5/3 + 1) + C = -5 * (u^{(-2/3)})/(2/3) + C = -15/2 * u^{(-2/3)} + C.\)
Finally, substituting back u = 7 - x^2 and applying the initial condition h(1) = -7, we can solve for the constant of integration C:
\(h(1) = -15/2 * (7 - 1^2)^{(-2/3)} + C = -7\).
Simplifying the equation and solving for C, we find:
\(-15/2 * 6^{(-2/3)} + C = -7\),
\(C = -7 + 15/2 * 6^{(-2/3)\)
Therefore, the function h(x) is given by:
\(h(x) = -15/2 * (7 - x^2)^{(-2/3)} + (-7 + 15/2 * 6^{(-2/3)}).\)
Learn more about derivative here: https://brainly.com/question/32963989
#SPJ11
Please help me to solve this question.

Answers
Answer:
A=266CM
Step-by-step explanation:
p=2l + 2w l=2x+1 w=x+5
66=2[2x+1] + 2{x+5] l=2x9 + 1 w=9+5
66=4x+2 + 2x+10 l=18+1 w=14
66=6x+12 l=19
66-12=6x
54=6x A=L x W
x=9 A=19 x 14
A=266CM
the probability of rolling factors of 6 on both dice
Answers
Answer:1/6
Step-by-step explanation:
is the following a probability model? what do we call the outcome "red"?
Answers
The following a probability model? what do we call the outcome No, the provided information is not sufficient to determine if it is a probability model. The outcome "red" is typically referred to as an event.
A probability model is a mathematical representation of a random experiment, where the sample space is defined, and probabilities are assigned to all possible outcomes. To determine if the given information is a probability model, we would need to know the complete list of possible outcomes, their corresponding probabilities, and ensure that the probabilities meet the necessary conditions (sum up to 1 and are non-negative).
Based on the limited information provided, we cannot determine if it is a probability model. The outcome "red" is called an event in the context of probability.
To know more about probability, visit:
https://brainly.com/question/30034780
#SPJ11
1. 48 students to 4 teachers Your answer
Answers
Answer:
12:1
Step-by-step explanation:
you have to simplify it
Solve for b. -9/3 + b = -1 b = ___?
Answers
Answer:
2
Step-by-step explanation:
its 2 have a good day (:
help!!!! I will give brainiest to whoever gets both
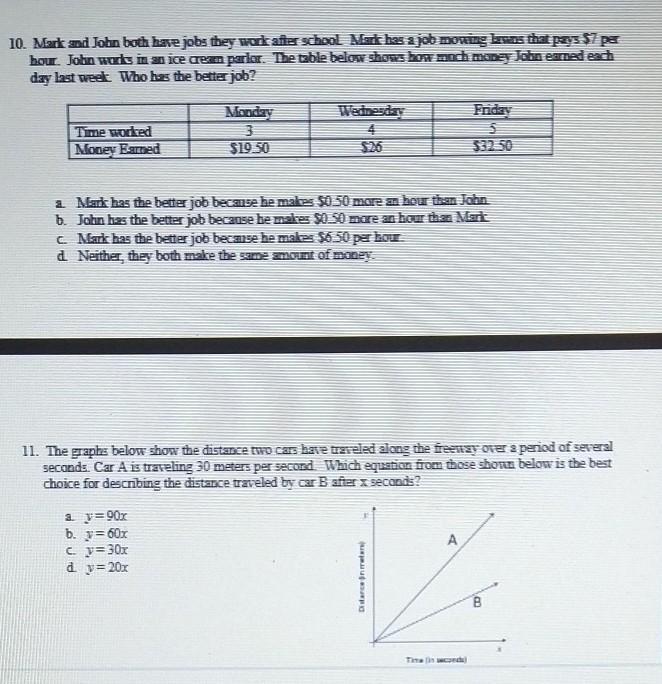
Answers
Answer:
they are both c
Step-by-step explanation:
Reduce to simplest form
3/2 + ( -6/5 ) = ?
Answers
Answer:
Step-by-step explanation: 3/2=1.5 (-6/5)=(-1.2) 1.5+(-1.2)=0.3
Answer=0.3
HELPP EASY MATH FOR Y GUYS IM 5 GRADE

Answers
Answer:
Step-by-step explanation:
for number 9.) 9r-45
HELP PLZ questions in pictures above

Answers
Answer:
S1) False. 2³ is 2 × 2 × 2 which is 8, not 6.
S2) False. ( 2x / 3y ^ (2) ) ^ (3) =
( (2x) ^ (3) / ( (3y) ^ (2) ) ^ (3) ) = (2)³ × (x)³ / (3)³ × (y²)³ = 8 × x³ / 27 × y⁶ = 8x³ / 27y⁶.
i.e (a^b)^c = a^(b × c).
S3) True.
S4) True.
S5) False. x^(-3) = 1 / x^(3) ≠ 1 / 3x
Can someone help? Thanks! It will be explained in the picture :)

Answers
Answer:
I think you multiply 4 by 5 ft
I say that because you do four times five then you have to do it all the way around and get that.
I don’t know if that is right though. SORRY!
What is the estimated answer to 8 x 7 divided by 0.5
Answers
Answer:
112
Step-by-step explanation:
8 x 7 = 56
56 divided by 0.5 is 112
8•7=56
56/0.5= 112