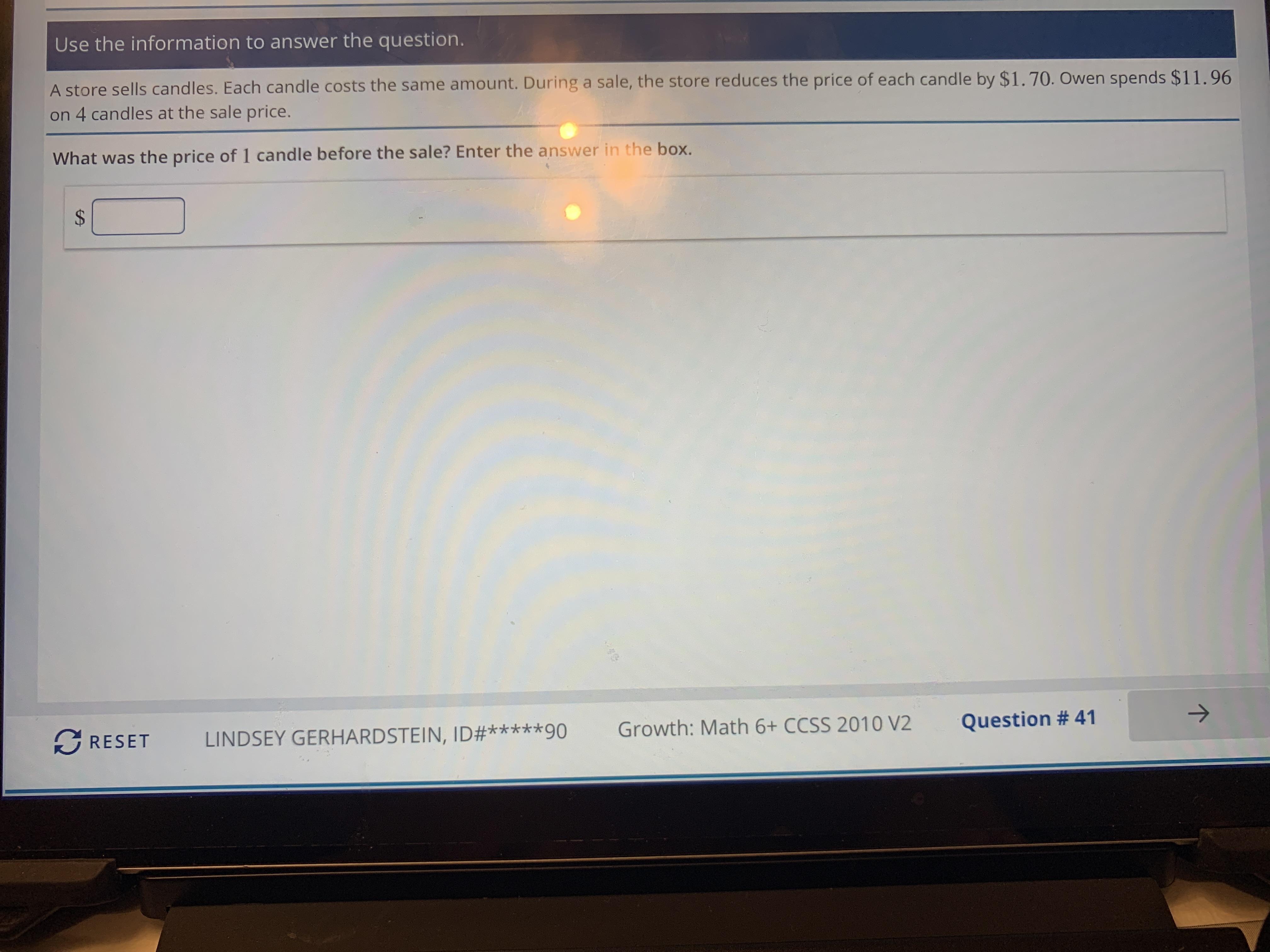
Answers
Answer:
$4.69
Step-by-step explanation:
HOPE THIS HELPEDDDD ❤✨
Answer:
The original price of the candles was $4.69
Step-by-step explanation:
$11.96 (price of 4 candles) ÷ 4 candles = $2.99 (how much each candle costs)
$2.99 (how much each candle costs) + $1.70 (how much the price of the candles lowered) = $4.69 (the old price per candle)
(hope I helped)
Related Questions
Please help with this quick

Answers
Answer:
2 x 1 + 3 = 5 or 2 x 1 + 3
that should be the answer
pls help.., Warren bought 172.57 ounces of flour and he used 76.7 ounces of it to make biscuits. How much is left?
Answers
Answer:
95.87 oz left
Step-by-step explanation:
172.57-76.7 = 95.87
A square purple rug has a green square in the center. The side length of the green square is x inches. The width of the purple band that surrounds the green square is 3 in. What is the area of the purple band?
Answers
\(n^{2} +3n-12=6\)
Answers
Answer:
Step-by-step explanation:
n² + 3n - 18 = 0
n = [-3 ±√(3²-4(1)(-18)]/[2(1)] = [-3 ±√81]/2 = 3, -6
Please help me on step 4

Answers
The beginning part of the question is missing and it says;
The measures of center can be used to summarize the number of pets that students own. Cameron asked eight of his classmates how many pets they own. The results are listed below.
1, 0, 2, 0, 3, 7, 0, 2, 4
Answer:
Median
Step-by-step explanation:
Let's rearrange the results from least to most.
0, 0, 0, 1, 2, 2, 3, 4, 7
Mode is the most occurring number which in this case is zero, so Cameron can't use that to convince his parents to get another pet.
Median is middle number and in this case is 2.
Mean is; sum of results/ number of results = 19/9 = 2.11
Thus, the best measure of tendency for Cameron to use is median.
she was considering purchasing the awesomeflex3000 for 889 using your function from question 1, what would charlotte be charlottes before tax cost with the deal? is it worth it for her to pay for the subscription to get 15% off? Explain your answer.
Answers
The 15% discount for home gym, and the $889 cost of the Flex 3,000 gives;
1. f(x) = 0.85•x + 139.95
2. With the deal, Charlotte's before tax cost is $895.6
The deal cost is more than the initial price making the deal not worth it.
How to find the discount after tax?1. We are given;
The percentage discount Charlotte gets = 15% = 0.15
Cost of the 6 months subscription = $139.95
Now, to get the function;
f(x) = Final before tax
x = Price of the home gym equipment
Therefore, using the discount of 15%, we will have;
f(x) = (1 - 0.15)x + 139.95
f(x) = 0.85x + 139.95
2. We are told that the cost of the Flex3000 is x = $889
Therefore;
f(889) = (0.85 × 889) + 139.95
f(889) = 895.6
Charlotte's before–tax cost with the deal will therefore be, $895.6
Since the workout channel holds no value to Charlotte, and then the deal cost is higher than the initial cost, then we can say that it isn't worth it for her to pay for the subscription to get the 15% discount
Read more about discount after tax at; https://brainly.com/question/28935716
#SPJ1
Complete question is;
Charlotte has been saving up to buy a home gym so she can work out at home without having to pay for a
gym membership or worry about travel when the weather is bad (she lives in Minnesota where it snows
frequently). One day, she sees an ad for a 15% off sale at a fitness equipment store and decides it's a great
time to buy the home gym! She notices the fine print says that to get the 15% off the home gym, she has to
pay $139.95 up front for a 6-month subscription to a workout channel, which holds no value to her.
1. Using function notation, write an expression for the final before-tax cost, f(x), of the purchase
based on the initial price, x, of the home gym equipment with this deal.
2. She was considering purchasing the Awesome Flex3000 for $889. Using your function from
question 1, what would Charlotte be Charlotte's before-tax cost with the deal? Is it worth it for
her to pay for the subscription to get 15% off? Explain your answer.
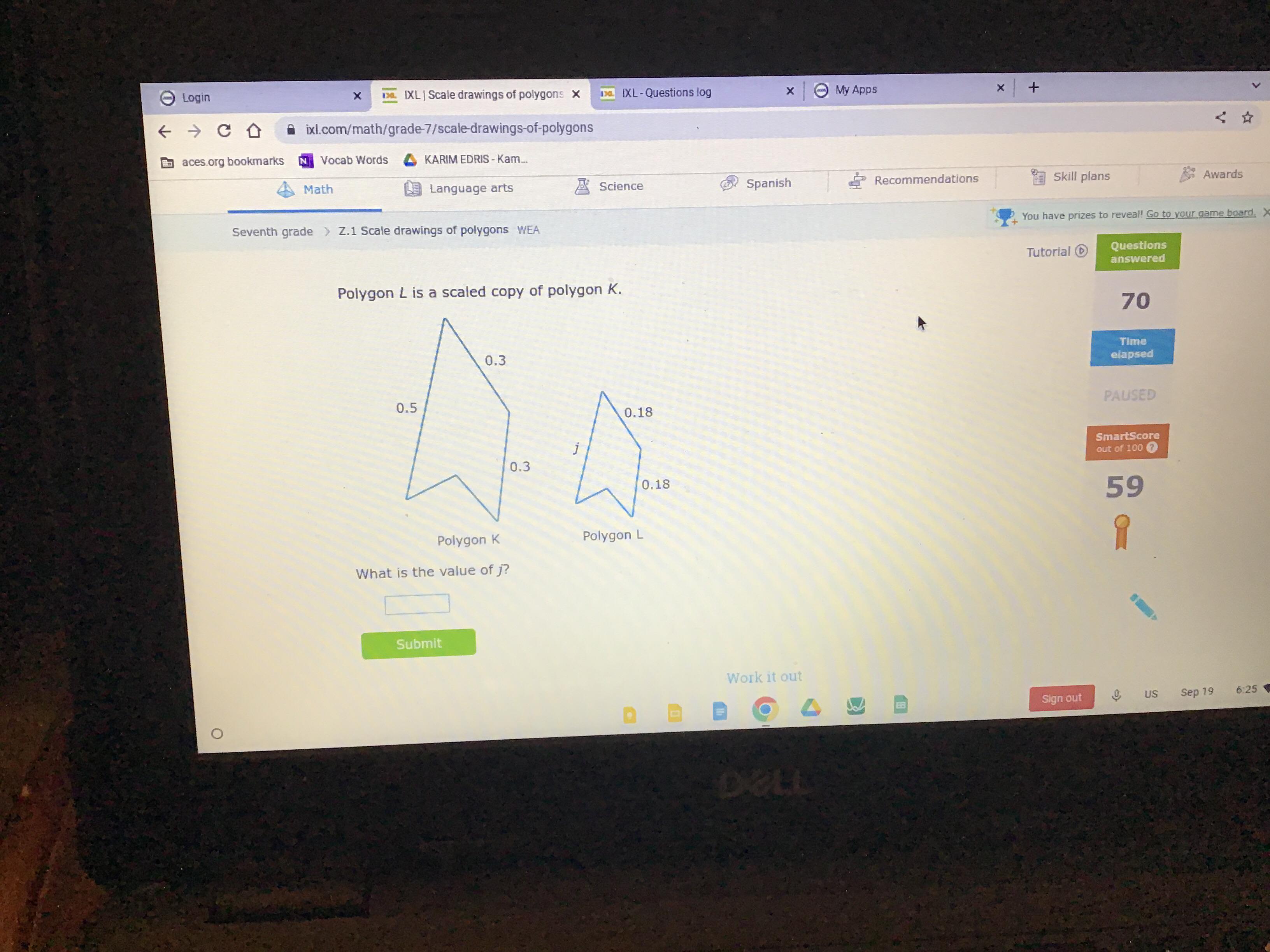
Polygon L is a scaled copy of polygon K.
What is the value of m?
Answers
It's not possible to determine the value of m without more information about the polygons in question. In order to solve for m, you would need to know the number of sides and the measures of the angles in both polygons, as well as the scale factor by which polygon L was scaled from polygon K. Without this information, it's not possible to determine the value of m.
The value of j in the scaled copy in the polygon is: 0.03.
How to Find the Sides of a Scaled Copy?When a figure is scaled, the corresponding dimensions of the new and original figures have a ratio that is the same because they are proportional to each other.
Polygon K and polygon L are similar polygons and therefore their corresponding side lengths are proportional.
The ratio below would be created:
j/0.5 = 0.18/3
Cross multiply
j = (0.5 × 0.18)/3
j = 0.09/3
j = 0.03
Therefore, the value of j in the scaled copy in the polygon is: 0.03.
Learn more about scaled copy on:
brainly.com/question/9762240
#SPJ2
The complete question is attached.
In each of Problems 1 through 10 find the general solution of the given differential equation. 1. y" – 2y' + y = 0 2. 9y" + 6y' + y = 0 3. 4y" – 4y' – 3y = 0) 4. 4y" + 12y' +9y = 0 5. y" – 2y' + 10y = 0) 6. y" – 6y' +9y = 0 7. 4y" + 17y' + 4y = 0 8. 16y" + 24y' +9y = 0 9. 25y" – 20y' + 4y = 0 10. 2y" + 2y' + y = 0
Answers
1) General solution for second order differential equation, y" – 2y' + y = 0, is y = (c₁x + c₂)eˣ .
2) General solution for differential equation, 9y" + 6y' + y = 0, is y =(c₁x + c₂)e⁻³ˣ.
3) General solution for differential equation, 4y"- 4y'- 3y = 0, is y = c₁ e⁶ˣ+ c₂e⁻⁴ˣ.
4) General solution for differential equation, 4y" + 12y' +9y = 0, is y = (c₁x + c₂)e⁻⁶ˣ.
5) General solution for differential equation, y" – 2y' + 10y = 0, is y = eˣ (c₁cos(6x) + c₂sin(6x)).
6) General solution for differential equation, y" – 6y' +9y = 0 is y = (c₁x + c₂)e³ˣ.
7) General solution for differential equation, 4y" + 17y' + 4y = 0, is y = c₁e⁻ˣ + c₂e⁻¹⁶ˣ.
8) General solution for differential equation, 16y" + 24y' +9y = 0, is y = (c₁x + c₂)e⁻¹²ˣ.
9) General solution for differential equation, 25y" – 20y' + 4y = 0, is y = (c₁x + c₂)e¹⁰ˣ.
10) General solution for differential equation, 2y" + 2y' + y = 0, is y = e⁻ˣ (c₁cos(2x) + c₂sin(2x)).
General solution is also called complete solution and complete solution = complemantory function + particular Solution
Here right hand side is zero so particular solution is equals to zero. Therefore, evaluating the complementary function will be sufficient to determine the general solution to the differential equation.
1) y"-2y' + y = 0, --(1)
put D = d/dx, so (D² - 2D + 1)y =0
Auxiliary equation for (1) can be written as, m² - 2m + 1 = 0 , a quadratic equation solving it by using quadratic formula,
\(m =\frac{-(- 2) ± \sqrt { 4 - 4}}{2}\)
=> m = 1 , 1
The roots of equation are real and equal. So, general solution is y = (c₁x + c₂)eˣ .
2) 9y" + 6y' + y = 0 or (9D² + 6D + 1)y =0 Auxiliary equation can be written as, 9m² + 6m + 1 = 0 , a quadratic equation solving it by using quadratic formula, \(m =\frac{ - (6) ± \sqrt {36 - 4×4}}{2}\)
=> m = - 6/2
=> m = -3 , -3
The roots of equation are real and equal. So, general solution is y = (c₁x + c₂)e⁻³ˣ.
3) 4y"- 4y'- 3y = 0
put D = d/dx, so (4D² - 4D - 3)y = 0
Auxiliary equation can be written as, 4m² - 4m - 3 = 0 , a quadratic equation solving it by using quadratic formula, \(m =\frac{-(-4) ± \sqrt {16 - 4×4×(-3)}}{2}\)
=> m = (4 ± 8)/2
=> m = -4 , 6
The roots of equation are real and equal. So, general solution is y = c₁ e⁶ˣ + c₂e⁻⁴ˣ.
4) 4y" + 12y' +9y = 0 or (4D² + 12D + 9)y= 0
Auxiliary equation can be written as, 4m² + 12m + 9= 0 , a quadratic equation solving it by using quadratic formula, \(m =\frac{-(12) ± \sqrt{144 - 4×4×9}}{2}\)
=> m = -12/2
=> m = -6 , -6
The roots of equation are real and equal. So, general solution is y = (c₁x + c₂)e⁻⁶ˣ.
5) y" – 2y' + 10y = 0 or (D² - 2D + 10)y = 0 Auxiliary equation can be written as, m² - 2m + 10 = 0 , a quadratic equation
solving it by using quadratic formula,
\(m =\frac{ - (-2) ± \sqrt {4 - 4×1×10}}{2}\)
=> m = (2 ± 6i)/2 ( since, √-1 = i)
=> m = 1 + 6i , 1-6i
The roots of equation are imaginary and unequal. So, general solution is y =eˣ (c₁cos(6x) + c₂sin(6x)).
6) y" – 6y' +9y = 0 or (D²- 6D + 9)y =0
Auxiliary equation can be written as, m² - 6m + 9 = 0 , a quadratic equation
solving it by using quadratic formula,
\(m =\frac{ - (-6) ± \sqrt {36 - 4×1×9}}{2}\)
=> m = 6/2 = 3,3
The roots of equation are real and equal. So, general solution is y = (c₁x + c₂)e³ˣ.
7) 4y" + 17y' + 4y = 0 or (4D²+ 17D + 4)y=0
Auxiliary equation can be written as, 4m² + 17m + 4 = 0 , a quadratic equation solving it by using quadratic formula, \(m =\frac{- (-17) ± \sqrt {16 - 4×4×17}}{2}\)
=> m = ( -17 ± 15)/2
=> m = (-17 + 15)/2, (- 17 - 15)/2= -1, -16
The roots of equation are real and unequal. So, general solution is y = c₁e⁻ˣ + c₂e⁻¹⁶ˣ.
8) 16y"+24y'+9y =0 or (16D²+ 24D + 9)y= 0
Auxiliary equation can be written as, 16m² + 24m + 9 = 0 , a quadratic equation solving it by using quadratic formula, \(m =\frac{ - (24) ± \sqrt {576 - 4×9×16}}{2}\)
=> m = (-24 ± 0)/2
=> m = -12,-12
The roots of equation are real and equal. So, general solution is y = (c₁x + c₂)e⁻¹²ˣ.
9) 25y"- 20y' +4y =0 or (25D²-20D + 4)y = 0
Auxiliary equation can be written as, 25m²- 20m + 4 = 0 , a quadratic equation solving it by using quadratic formula, \(m =\frac{ - (-20) ± \sqrt {400 - 4×4×25}}{2}\)
=> m = 20/2
=> m = 10 , 10
The roots of equation are real and equal. So, general solution is y = (c₁x + c₂)e¹⁰ˣ.
10) 2y" + 2y' + y = 0 or (2D²+ 2D + 1)y =0
Auxiliary equation can be written as, 2m² + 2m + 1 = 0 , a quadratic equation solving it by using quadratic formula, \(m =\frac{ - (2) ± \sqrt {4 - 4×1×2}}{2}\)
=> m = (- 2 ± 4i)/2 ( since, √-1 = i)
=> m = -1 + 2i , -1 - 2i
The roots of equation are imaginary and unequal. So, general solution is y = e⁻ˣ (c₁cos(2x) + c₂sin(2x)). Hence, required solution of differential equation is y = e⁻ˣ (c₁cos(2x) + c₂sin(2x)).
For more information about general solution of differential equation, visit:
https://brainly.com/question/30078609
#SPJ4
At a school carnival, the diameter of the mat of a trampoline is 16 feet and the diameter of its metal frame is 18 feet. What is the length, in feet, of the metal frame that surrounds the trampoline? Use 3. 14 for π and round your answer to the nearest tenth. 50. 2 feet 56. 5 feet 100. 5 feet 113. 0 feet.
Answers
Answer:
(b) 56.5 ft
Step-by-step explanation:
The circumference of a circle of diameter d is given by ...
C = πd
For the given diameter, the circumference of the frame is ...
C = (3.14)(18 ft) ≈ 56.52 ft
The length of the outside edge of the frame is about 56.5 feet.
A daycare charges $195 per week for each child that attends. There are 51 children that attend each week.
What is the best estimate for the total amount of money the daycare receives each week?
A. $5,000
B. $7,000
C. $10,000
D. $15,000
Answers
Answer:
c
Step-by-step explanation:
195 x 51 =9945
estimated = 10,000
195 x 51= 9945
So the estimated number is 10,000
Select all the true sentences!!!

Answers
Answer:
the second one and third one
Step-by-step explanation:
solve the equation 4x^3 + 32x^2 + 42x - 16 = 0, given that one root is equal to the sum of the other two roots
Answers
The solutions to the equation are x = -1, x = -8, and x = 1/2.
How to calculate the valueThe equation 4x³ + 32x² + 42x - 16 = 0 can be divided throuh by 2 as follows:
2x³ + 16x² + 21x - 8 = 0
We can test each of these possible roots by substituting them into the equation and seeing if we get 0. When we substitute -1, we get 0, so -1 is a root of the equation. We can then factor out (x + 1) from the equation to get:
(x + 1)(2x² + 15x - 8) = 0
We can then factor the quadratic 2x² + 15x - 8 by grouping to get:
(x + 8)(2x - 1) = 0
This gives us two more roots, x = -8 and x = 1/2.
Therefore, the solutions to the equation are x = -1, x = -8, and x = 1/2.
Learn more about equations on
https://brainly.com/question/2972832
#SPJ1
Use technology to find points and then graph the function with at least 5 points y=(x+2)^2-2
Answers
The function y=(x+2)²-2 is graphed accordingly.
What is a graph?Graphs are an excellent tool for visualizing data and displaying statistics.
For the function above, here are it's traits
Vertex: The vertex of the graph is located at (-2, -2), which is obtained from the equation as (-2, -2).
Shape - The graph represents a parabola that opens upwards. This is because the coefficient of the squared term (x²) is positive.
Axis of Symmetry - The axis of symmetry is a vertical line passing through the vertex. In this case, the axis of symmetry is x = -2.
Minimum Point - The vertex (-2, -2) represents the minimum point of the graph. This is the lowest point on the parabola.
Range - The range of the function is all real numbers greater than or equal to -2. In other words, the graph extends infinitely downwards.
Learn more about graph at:
https://brainly.com/question/25799000
#SPJ1

Jamal likes to draw whenever he has spare time during the school day. So, he brings his drawing supplies to each class in a pencil box shaped like a rectangular prism. The pencil box is 13 inches long and 5 inches tall, and it has a volume of 162.5 cubic inches.
Answers
Answer:
Hope this help........
Step-by-step explanation:
The volume of a rectangular prism V is the product of its length ℓ, width w, and height h.
V=ℓwh
The pencil box is shaped like a rectangular prism. Its length is 13 inches, its height is 5 inches, and its volume is 162.5 cubic inches.
To find how wide the pencil box is, w, you can use the formula for the volume of a rectangular prism.
V
=ℓwh
162.5
=13w5
Solve for w.
162.5
=13w5
162.5
=65w Multiply 13 by 5 x 162.5 x 65 = 65w
65
Divide both sides by 65
2.5
= w Simplify
The pencil box is 2.5 inches wide.

What two angles of elevation will enable a projectile to reach a target 13 km downrange on the same level as the gun if the projectile's initial speed is 425 m/sec? The two angles of elevation are___° and___°
(Round to the nearest degree. Use ascending order.)
Answers
In this cases, The two angles of elevation are 36° and 144°
How to find the angles of elevationTo find the two angles of elevation for a projectile to reach a target 13 km downrange with an initial speed of 425 m/sec, we can use the projectile motion formula:
range (R) = (v² * sin(2 * angle)) / g
where v is the initial speed (425 m/sec), angle is the angle of elevation, and g is the acceleration due to gravity (approximately 9.81 m/s²).
We need to solve for angle.
First, convert the range to meters:
13 km = 13,000 m.
Next, plug the values into the formula:
13,000 = (425² * sin(2 * angle)) / 9.81
Now, solve for angle:
sin(2 * angle) = (13,000 * 9.81) / 425²
sin(2 * angle) ≈ 0.7387
Now, find the two angles using the arcsin function:
2 * angle = arcsin(0.7387)
angle = 0.5 * arcsin(0.7387)
There are two angles that will result in the same range:
angle_1 = 0.5 * arcsin(0.7387)
angle_2 = 180 - angle_1
Calculating the values:
angle_1 ≈ 36° angle_2 ≈ 144°
So, the two angles of elevation that will enable a projectile to reach a target 13 km downrange on the same level as the gun with an initial speed of 425 m/sec are approximately 36° and 144°.
Learn more about angle of elevation at
https://brainly.com/question/12951657
#SPJ11
You have one type of chocolate that sells for $2.50/1b and another type of chocolate that sells for $8.50/lb. You would like to have 36 lbs of a chocolate mixture that sells for $6.40/1b. How much of each chocolate will you need to obtain the desired mixture? You will need lbs of the cheaper chocolate and lbs of the expensive chocolate.
Answers
We have the next information
First type of chocolate $2.50 per lb
Second type of choclate 8.50 per lb
x= lbs of the cheaper chocolate
y=lbs of the expensive chocolate
36 total pounds
x+y=36
2.50(x)+8.50(y)=36(6.40)
2.5x+8.5y=230.4
then we solve the equation system
x+y=36 .....(1)
2.5x+8.5y=230.4 ....(2)
we clear x from the first equation
x=36-y
we substitute the equation above in the second equation
2.5(36-y)+8.5y=230.4
90-2.5y+8.5y=230.4
we clear y
6y=230.4-90
6y=140.4
y=140.4/6
y=23.4
then we substitute the value of y in the next equation
x=36-y=36-23.4
x=12.6
you will need 12.6 lbs of the cheaper chocolate and 23.4 lbs of the expensive chocolate
Let X be a binomial random variable with n =
25 and p = 0.01.
a.
Use the binomial table to find P(X = 0),
P(X = 1), and P(X = 2).
b.
Find the variance and standard deviation of X.
Answers
a. probabilities using the binomial table: 0.0225
b. standard deviation of a binomial random variable is given by: 0.4975
a. Calculation of probabilities using the binomial table:
The probability of X=0, P(X=0) can be found using the binomial table.
The probability of X=1 and X=2 can be found using the formula:
P(X = k) = (n choose k) * (p)^k * (1-p)^(n-k)
Where n = 25 and p = 0.01.
P(X = 0) = (25 choose 0) * (0.01)^0 * (0.99)^(25-0)= (1) * (1) * (0.78) = 0.78
P(X = 1) = (25 choose 1) * (0.01)^1 * (0.99)^(25-1)= (25) * (0.01) * (0.77) = 0.1925
P(X = 2) = (25 choose 2) * (0.01)^2 * (0.99)^(25-2)= (300) * (0.0001) * (0.75) = 0.0225
b. Calculation of the variance and standard deviation of X:
The variance of a binomial random variable is given by:
Var(X) = np(1-p)
Where n = 25 and p = 0.01.
Var(X) = 25 * 0.01 * (1 - 0.01) = 0.2475
The standard deviation of a binomial random variable is given by:
SD(X) = sqrt(np(1-p))
SD(X) = sqrt(25 * 0.01 * (1 - 0.01))
= sqrt(0.2475) = 0.4975 (rounded to 4 decimal places)
To know more about binomial table visit:
https://brainly.com/question/30100291
#SPJ11
Of the 245 7th graders, 40% of them are in band. How many 7th graders are in band?
Answers
Explanation:
1. Turn 40% into a decimal by removing the “%” and placing “0.” In front of it. (0.4)
2. Multiply the decimal (0.4) by the number of students (245) to get the answer. (0.4x245=98)
Plz write this on paper help me and send it❤️


Answers
Answer:
1. \(27^{\frac{2}{3} } =9\)
2. \(\sqrt{36^{3} } =216\)
3. \((-243)^{\frac{3}{5} } =-27\)
4. \(40^{\frac{2}{3}}=4\sqrt[3]{25} =4325\)
5. Step 4: \((\frac{343}{27}) ^{-1} =\frac{27}{343}\)
6. \(D. -72cd^{7}\)
Step-by-step explanation:
Use the following properties:
\(a^{\frac{x}{y} } =\sqrt[x]{a^{y} }\)
\(\sqrt[n]{ab} =\sqrt[n]{a} \sqrt[n]{b}\)
\(a^{-n} =\frac{1}{a^{n} }\)
\((xy)^{z} =x^{z} y^{z} \\\\\)
\((x^{y}) ^{z} =x^{yz}\)
\(x^{y} x^{z} =x^{y+z}\)
So:
1. \(27^{\frac{2}{3} } =\sqrt[3]{27^{2}} =\sqrt[3]{729} }=9\)
2. \(\sqrt{36^{3} } =\sqrt{36*36*36} =\sqrt{36} \sqrt{36} \sqrt{36} =6*6*6=216\)
3. \((-243)^{\frac{3}{5} } =\sqrt[5]{-243^{3} } =\sqrt[5]{-14348907} =-27\)
4. \(40^{\frac{2}{3}}=\sqrt[3]{40^{2} } =\sqrt[3]{2^{6} 5^{2} } =\sqrt[3]{2^{6} } \sqrt[3]{5^{2} } =2^{\frac{6}{3} } 5^{\frac{2}{3} } =4 *5^{\frac{2}{3} } =4\sqrt[3]{5^{2} } =4\sqrt[3]{25}=4325\)
5. \((\frac{343}{27}) ^{-1} =\frac{1}{\frac{343}{27} } =\frac{27}{343}\)
6.
\((-8c^{9} d^{-3} )^{\frac{1}{3} } *(6c^{-1}d^{4})^{2} =\sqrt[3]{-8} c^{3} d^{-1} 36c^{-2} d^{8} \\\\-2c^{3} d^{-1} 36c^{-2} d^{8}=-72cd^{7}\)
Please help I will mark brainiest ✅

Answers
Answer:
y=-2x-3
the line is going downwards which makes the slop a negative value
Step-by-step explanation:
A shipping container will be used to transport several 120-kilogram crates across the country by rail. The greatest weight that can be loaded into the container is 27500 kilograms. Other shipments weighing 12400 kilograms have already been loaded into the container. Which inequality can be used to determine x, the greatest number of
120-kilogram crates that can be loaded onto the shipping container?
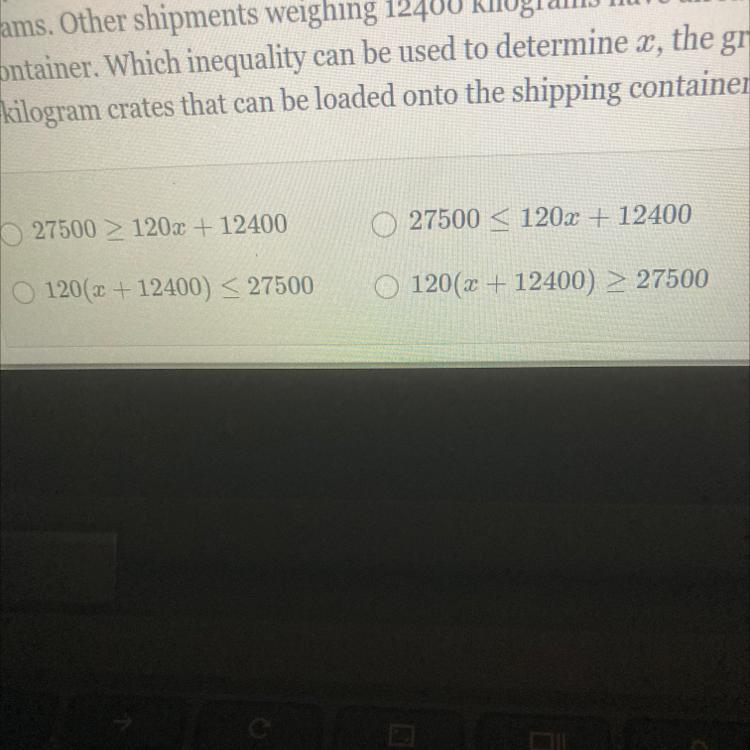
Answers
Inequality can be used to determine x, the greatest number of 120-kilogram crates that can be loaded onto the shipping container is 8000 + 120C <= 27500
What is inequality?An inequality is a relationship that allows us to contrast two or more mathematical expressions.
Knowing that;
Each carton weighs 120 kg.
The container's maximum weight when loaded is 27500 kg.
Weight of the container as it is currently loaded: 8000 kg
Now that we have merged, we have;
Solution
because 8000 grams have already been loaded kilograms
into the container
each crate weighs 120 kilograms.
so 8000 + 120C <= 27500
To learn more about inequality refer to:
https://brainly.com/question/28862943
#SPJ1
Find x, and GH.
X =
GH: =
34
7x + 6
4x + 8

Answers
By using given figure, x=9/4 and the length of GH = 21.75.
What is the length ?
Here, in given figure,
BG≈GF and CH≈HE
now by using these similarities, we can write as,
BG≈GF therfore, \(\frac{GF}{BG}\) = 1:1
\(\frac{GF}{BF}\)=\(\frac{4x+8}{34}\)
1/2=\(\frac{4x+8}{34}\)
8x+16=34
8x= 18
x=9/4
if x=9/4 then,
GH= 7x+6 = 7(9/4)+6 =63/4+6 =\(\frac{63+24}{4}\) = 21.75
What is similarity of sides?
similarity of sides refers to the property of two geometric shapes or figures having the same shape but not necessarily the same size. More specifically, two shapes are said to be similar if their corresponding angles are congruent and their corresponding sides are proportional in length.
To know more baout similarities, visit:
https://brainly.com/question/9753824
#SPJ1
HELP!!
Also introduce each terms provided in option!

Answers
The error expression of |A - N| in the given problem is: Absolute Error
How to identify the mathematical error?The absolute error is gotten by subtracting the true value from the measured value. The answer is normally expressed as ± or with an absolute value sign. The absolute error equation is expressed as: Absolute error = |measured value - true value|
Relative error is defined as a measurement of error that depends on the absolute error of a measuring tool as well as a measured value. Relative error can thus be defined as a decimal or as a percentage.
Now, we are told that
A is an actual value.
N is near the value,
From the definition of absolute error, we can clearly state that |A - N| is known as absolute error.
Read more about Mathematical error at: https://brainly.com/question/28771966
#SPJ1
Use the distributive property to remove the parentheses.
7c^2(2-9c^4)
Simplify your answer as much as possible.
Answers
The simplified expression after applying the distributive property and removing the parentheses is\(14c^2 - 63c^6\)
A fundamental mathematical concept known as the distributive property explains how to expand the product of a number and the sum or difference of additional numbers. It claims that the equation a * (b + c) is equal to a * b + a * c for any three numbers, a, b, and c. The statement a * (b - c) has the same meaning as a * b - a * c. In other words, you can multiply any term included in brackets independently. The distributive property is frequently employed in algebraic operations, expression simplification, and term expansion to solve equations. It serves as the foundation for many calculations and mathematical processes.
Let's use the distributive property to remove the parentheses and simplify the expression.
Given expression: \(7c^2(2-9c^4)\)
Step 1: Apply the distributive property by multiplying \(7c^2\) with each term inside the parentheses.
\(7c^2 * 2 - 7c^2 * 9c^4\)
Step 2: Perform the multiplication.
\(14c^2 - 63c^6\)
So, the simplified expression after applying the distributive property and removing the parentheses is \(14c^2 - 63c^6\)
Learn more about distributive property here:
https://brainly.com/question/16566992
#SPJ11
due in 5 minutes 12-3y< 27
Answers
Answer:
y > -5
Step-by-step explanation:
Given the following facts about the moment generation Max+b) (+) . et My lat). If a normal random Variable, with mean cand stand and deviation d, (I) then My (4) variable and standard with mean Mr deviation bx = 4, and that y=34+5. use the moment generating & unction uniqueness theoren, and facts (I) and (IT) above to prove that is a normal random variable.
Answers
Since the mean and variance of y are the same as those of a normal random variable, y is a normal random variable.
The given moment generating function is Mx(t) = e^(t(4 + 5t + 17t^2/2)), where t is the moment. The moment generating function of a normal random variable is given by Mx(t) = e^(μt + σ^2t^2/2).Comparing the two, we get:μ = 4σ^2 = 17/2We can now compute the first and second moments of y, using the moment generating function: My(t) = e^(t(34 + 5t)) × e^(t(4 + 5t + 17t^2/2))= e^(34t + 9t^2 + 17t^3/2 + 4t + 5t^2) = e^(34t + 14t^2 + 17t^3/2)So,μy = My(0) = 1 and σy^2 = My''(0) - My'(0)^2= (17/2) - 4 = 9/2
Since the mean and variance of y are the same as those of a normal random variable, y is a normal random variable.
This completes the proof using the moment generating function uniqueness theorem.
To know more about variance visit:
https://brainly.com/question/9304306
#SPJ11
The moment generating function (MGF) of a random variable is a mathematical function that uniquely defines the probability distribution of that variable. Therefore, if the MGF of a random variable is the same as that of a known distribution, the random variable follows that distribution.
This is known as the uniqueness theorem of moment generating functions.
Using the given moment generating function of a random variable X (Max+b)(+).etMy.lat), we need to prove that X follows a normal distribution. Here, Max+b = a, My = m, and = s (standard deviation).
Using the MGF, we can find the moments of the distribution. Differentiating the MGF 'n' times gives the nth moment about zero. We can use this to find the mean and variance of the distribution.
Therefore, the mean of the distribution is the first derivative of the MGF at t=0,
and the variance is the second derivative of the MGF at t=0.
Using facts (i) and (ii), we can write the MGF of X as:
(Mx(t)) = [(b + mt) + a(s^2 + m^2)/2] / [(s^2/2) + (t^2/2)]
Taking the first derivative of Mx(t) and substituting t=0, we get:
\(E(X) = [(b + m*0) + a(s^2 + m^2)/2] / [(s^2/2) + (0^2/2)]E(X) = (b + am) / (s^2/2) + 0E(X) = (2(b + am))/s^2\)
This gives us the mean of the distribution as
(2(b + am))/s^2
Taking the second derivative of Mx(t) and substituting t=0, we get:
\(Var(X) = [(b + m*0) + a(s^2 + m^2)/2] / [(s^2/2) + (0^2/2)]Var(X) = [a(s^2 + m^2)/2] / (s^2/2) + 0Var(X) = a(s^2 + m^2)/s^2 - 1\)
We know that the MGF of a normal distribution with mean m and variance s^2 is given by:
\((Mn(t)) = e^(mt + s^2t^2/2)\)
Comparing this with the given MGF of X, we see that they are equal.
Therefore, X follows a normal distribution with mean (2(b + am))/s^2 and variance a(s^2 + m^2)/s^2 - 1.
To know more about random variable, visit:
https://brainly.com/question/30789758
#SPJ11
factoring integers with sublinear resources on a superconducting quantum processor
Answers
Factoring integers with sublinear resources on a superconducting quantum processor can be achieved using quantum approximate optimization algorithm" (QAOA) or quantum phase estimation algorithm (QPE) approach.
Factoring integers with sublinear resources on a superconducting quantum processorFactoring large integers is a problem of significant importance in the field of cryptography.
Classical computers have limited efficiency in solving this problem, and their performance is expected to decline further as the size of the integers to be factored increases.
In contrast, quantum computers are expected to have exponential speedup in factoring large integers, thanks to Shor's algorithm.
Recently, researchers have been exploring the possibility of using superconducting quantum processors to factor integers with sublinear resources.
One approach is to use a so-called "quantum approximate optimization algorithm" (QAOA), which maps the problem of factoring integers to a problem of finding the ground state of a certain Hamiltonian.
The QAOA can be implemented using a superconducting quantum processor, with the problem Hamiltonian implemented by a set of two-qubit gates.
Another approach is to use the quantum phase estimation algorithm (QPE) to estimate the eigenvalues of the problem Hamiltonian.
This can be used to factor integers by finding the period of a certain function using the quantum Fourier transform, as in Shor's algorithm. QPE can be implemented on a superconducting quantum processor using phase estimation circuits, which require only polynomial resources.
Learn more about superconducting quantum processors on:
brainly.com/question/29235650
#SPJ1
Tell whether the angles are complementary or supplementary. Then find the value of x.

Answers
Answer:
The angles are supplementary.
x = 31
Step-by-step explanation:
The way the two angles lay together and make a straight line shows that they are supplementary. Supplementary means that they add up to 180°
Use this idea to write an equation.
2x + 3x + 25 = 180
combine like terms
5x + 25 = 180
subtract 25
5x = 155
divide by 5
x = 31
Answer:
x = 31
Step-by-step explanation:
(3x + 25) and 2x are a linear pair and are supplementary, that is
3x + 25 + 2x = 180
5x + 25 = 180 ( subtract 25 from both sides )
5x = 155 ( divide both sides by 5 )
x = 31
2
Which equation represents a line with a slope of
and a y-intercept of
12
5
2
7
Help me pls
Answers
Answer:
2
Step-by-step explanation:
15 POINTS!!!
Solve each equation by graphing the related function. If the equation has no real-number solution, write no solution.
#1
x^2-9=0
A. X13
B. X-19
C. X-0
D. no solution
Solve each equation by finding the square root. If the equation has no real-number solution, write no solution.
#5
4g^2=25
A. g=+1/2
B. g=+1/3
C. g=+5/2
D. No solution
#6
64b^2=16
A. b=+1/4
B.b=+1/2
C.b=+1/8
D. No solution
Tell me how many solutions the equation has.
#9
h^2=-49
A. One solution
B. Two solutions
C. No solution
#10
S^2-35=-35
A. One solution
B. Two solutions
C. No solution
Answers
Answer:
1. D. no solution
5. C. g=+5/2
6. B. b=+1/2
9. C. no solution
10. A. one solution