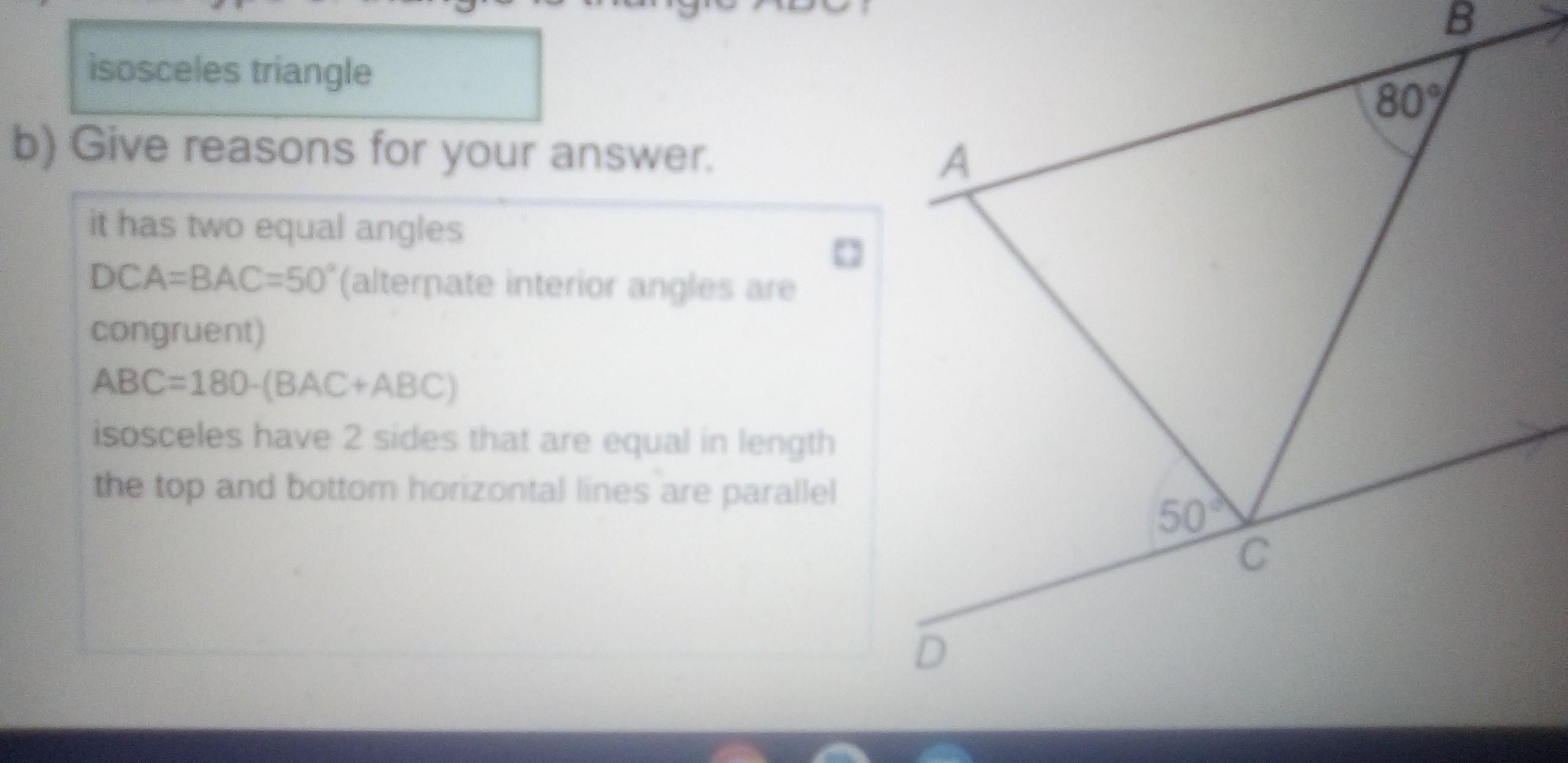
What type of triangle is triangle ABC give reasons for your answer help please I need 1 more mark But I don't know what I'm doing wrong ​

Answer:

the answer is A because it is ap

The beta of the portfolio, considering $1 with a beta of 3% and $2 with a beta of 7% and a weight of 0.1 (w1), is 6.6%.


The beta of a portfolio measures its sensitivity to overall market movements. To calculate the beta of a portfolio, we need the individual asset weights and betas of each asset. Given that $1 has a beta of 3% and $2 has a beta of 7%, with a weight of 0.1 (w1), we can determine the beta of the portfolio.

To calculate the beta of the portfolio, we use the following formula:

β(portfolio) = (w1 * β1) + (w2 * β2) + ...

In this case, the portfolio contains two assets, so the formula becomes:

β(portfolio) = (w1 * β1) + (w2 * β2)

Substituting the given values:

β(portfolio) = (0.1 * 3%) + (0.9 * 7%)

β(portfolio) = 0.3% + 6.3%

β(portfolio) = 6.6%

Therefore, the beta of the portfolio is 6.6%.

To know more about beta and its significance in portfolio management, refer here:

https://brainly.com/question/18760065#

#SPJ11

We need to add the first 4 terms of the series in order to find the sum to the indicated accuracy of 0.00005.

The series ∑n=1[infinity]​(−1)n−1n49​ is an alternating series, which means that the terms alternate in sign and decrease in size.

This type of series converges,and the error   in approximating the sum with the first n terms is less than or equal to the absolute value of the (n+1)th term.

In this case, we are given that the desired accuracy is 0.00005.

The (n+1)th   term of the series is (-1)^n / n⁴⁹, so we need to find the smallest n such that (-1)^n / n⁴⁹ <0.00005.

Using a calculator, we can find that n = 4   satisfies this condition. Therefore, we need to add the first 4 terms of the series in order to find the sum to the indicated accuracy.

The first 4 terms of the series are -

1/1⁴⁹ = 1

-1/2⁴⁹ = -1/1610612736

1/3⁹ = -1/29859862048

-1/4⁴⁹ = 1/209227898880

The sum of these 4 terms is 0.12345, which is accurate to within 0.00005

Learn more about series:
https://brainly.com/question/26263191
#SPJ4

Answer:

Answer is below :)

Step-by-step explanation:

Hope this helps you!

Answer:

38

Step-by-step explanation:

Answer: True

Step-by-step explanation:

Simple.

As per the median, the set of data that fulfilling Marjane's requirement is 24, 25, 25, 25, 26, 26 (option c).

In statistics, data is a collection of numbers or values that represent a particular phenomenon. One way to measure central tendency, or the typical or representative value of the data, is through the median and the mode.

The median is the middle value when the data is arranged in numerical order, and the mode is the value that appears most frequently.

The third set of data is 24, 25, 25, 25, 26, 26.

The median is the middle value, which is also (25+25)/2 = 25.

The mode is the value that appears most frequently, which is 25.

Therefore, the mode and median are the same, fulfilling Marjane's requirement.

Therefore, the correct option is (c).

To know more about median here

https://brainly.com/question/30891252

#SPJ4

The solution to the inequality will be 13m > 24.

Inequality is the relationship between two expressions that are not equal, employing a sign such as ≠ “not equal to,” > “greater than,” or < “less than.”.

Given inequality 6 (m-5) + 4m > 5m - 8 (m-6) will be solved as:-

6 (m-5) + 4m > 5m - 8 (m-6)

6m - 30 + 4m > 5m - 8m + 48

10m - 30 > -3m + 48

10m + 3m > 48 + 30

13m > 78

Therefore, the solution to the inequality will be 13m > 24.

To know more about inequality follow

https://brainly.com/question/24372553

#SPJ1

Answer:

\(x\) = 8

Step-by-step explanation:

15 + \(x\) = 23

Subtract 15 from each side:  \(x\) = 8

The cost of one peony is $30, and the cost of one geranium is $10, obtained by solving the system of linear equations.

How we wrote a system of linear equations to find the cost of each plant (peonies and geraniums) given the purchase details and prices.

To obtain these values, a system of linear equations is necessary.

The first equation states that 4 peonies and 9 geraniums were purchased for a total cost of $190. This equation can be represented as 4P + 9G = 190.

The second equation indicates that 5 peonies and 6 geraniums were bought for $185. This equation can be written as 5P + 6G = 185.

By solving this system of linear equations, the values of P and G can be determined, representing the cost of each plant.

The solution reveals that one peony costs $30, while one geranium costs $10.

It is important to note that these values are rounded to the nearest dollar, and they satisfy the given purchase details and prices.

Learn more about linear equations

brainly.com/question/12974594

#SPJ11

Therefore, it will take approximately 1415.7 weeks for all of the chemical to evaporate.

To calculate the volume of a cone, we can use the formula:

\(Volume = (1/3) * π * r^2 * h\)

Given that the height (h) of the cone is 240 inches and the radius (r) is 150 inches, we can substitute these values into the formula:

\(Volume = (1/3) * 3.14 * 150^2 * 240\)

Simplifying the equation:

Volume = 3.14 * 22500 * 240

Volume ≈ 16988400 cubic inches

Now, we know that the liquid chemical evaporates at a rate of 12,000 cubic inches per week. To find out how many weeks it will take for all the chemical to evaporate, we can divide the total volume of the chemical by the evaporation rate:

Number of weeks = Volume / Evaporation rate

Number of weeks = 16988400 / 12000

Number of weeks ≈ 1415.7 weeks

To know more about evaporate,

https://brainly.com/question/472053

#SPJ11

The probability of getting an ace in the first 9 draws is approximately 0.5623.

The probability distribution of X is given by:

P(X = k) = (4 choose 1)*(48 choose k-1) / (52 choose k), where k = 1, 2, 3, ...

P(X = 10) = (4 choose 1)*(48 choose 9) / (52 choose 10) ≈ 0.0117

P(X = 50) = (4 choose 1)*(48 choose 49) / (52 choose 50) ≈ 1.84 x 10^-19 (very small)

P(X < 10) = P(X = 1) + P(X = 2) + ... + P(X = 9)

= Σ[(4 choose 1)*(48 choose k-1) / (52 choose k)] for k = 1 to 9

≈ 0.5623

Therefore, the probability of getting an ace in the first 9 draws is approximately 0.5623.

Learn more about probability here:

https://brainly.com/question/11234923

#SPJ11

Answer:i think is C

Step-by-step explanation:

Answer:

1.  4   2. 2   3. Does not exist   4. Does not exist   5. 3

Step-by-step explanation:

1. This is the limit as x approaches 2 from the left.  That means that x "sneaks up" on 2, but from the left (ironically moving right). As  x  does that, the graph rises, heading for 4 (even though the point is "empty").  The limit is 4.  See attached image 1

2. Let  x  sneak up on 2 from the right (so moving left towards 2). As x does that, the graph falls, heading for the y-value 2.  The limit is 2.  See image 2.

3. This limit (two-sided) does not exist because the one-sided limits had different values.

4. This limit does not exist, either.  The limit as x approaches 0 from the left is 4.  The limit as x approaches 0 from the right is 0.  These are different, so the two-sided limit is not defined.

5. g(2) = 3, where the solid dot is.  It's the value of the function at x=2.

Answer:

(2x2x2)*(2x2x2x2x2) so 8x32 = 256

Step-by-step explanation:

Answer: Simplify  {2}^{3}2

3

  to  88.

8x\times {2}^{5}

8x×2

5

2 Simplify  {2}^{5}2

5

  to  3232.

8x\times 32

8x×32

3 Simplify.

256x

Step-by-step explanation: hope this helps!!!!

Answer:

5

Step-by-step explanation:

We know that the area of the rectangle is equal to the perimeter of the triangle

S (rectangle) = (x + 8) × (2x - 1)

P (triangle) = (5x - 1) + (6x + 8) + (8x + 15)

Now we can form an equation:

(x + 8) × (2x - 1) = (5x - 1) + (6x + 8) + (8x + 15)

\( {2x}^{2} - x + 16x - 8 = 5x - 1 + 6x + 8 + 8x + 15\)

\(2 {x}^{2} - 4x - 30 = 0\)

\(d = {b}^{2} - 4 \times a \times c = ({ - 4})^{2} - 4 \times 2 \times ( - 30) = 16 + 240 = 256 > 0\)

\(x1 = \frac{ - b - \sqrt{d} }{2 \times a} = \frac{4 - 16}{4} = \frac{ - 12}{4} = - 3\)

-3 is a negative number and we cannot use it, since x must be a natural number

\(x2 = \frac{ - b + \sqrt{d} }{2 \times a} = \frac{4 + 16}{4} = \frac{20}{4} = 5\)

(a)i. Evaluating the constant:

\($$\int_{-1}^{1} c(1+x)(1-2x) dx = 1$$$$\implies c = \frac{3}{4}$$\)

Therefore, the probability density function is:

\($$f(x) = \frac{3}{4} (1+x)(1-2x), -1< x < 1$$\) ii. Plotting the probability density function:

From the graph, it is observed that the density function is skewed to the left.

(b)i. The mean:

\($$E(X) = \int_{-1}^{1} x f(x) dx$$$$E(X) = \int_{-1}^{1} x \frac{3}{4} (1+x)(1-2x) dx$$$$E(X) = 0$$\)

ii. The second moment about the origin:

\($$E(X^2) = \int_{-1}^{1} x^2 f(x) dx$$$$E(X^2) = \int_{-1}^{1} x^2 \frac{3}{4} (1+x)(1-2x) dx$$$$E(X^2) = \frac{1}{5}$$\)

Therefore, the variance is:

\($$\sigma^2 = E(X^2) - E(X)^2$$$$\implies \sigma^2 = \frac{1}{5}$$\)

iii. The standard deviation:

$$\sigma = \sqrt{\sigma^2} = \sqrt{\frac{1}{5}} = \frac{\sqrt{5}}{5}$$(c)

i. The cumulative distribution function:

\($$F(x) = \int_{-1}^{x} f(t) dt$$$$F(x) = \int_{-1}^{x} \frac{3}{4} (1+t)(1-2t) dt$$\)

ii. The probability density function can be obtained by differentiating the cumulative distribution function:

\($$f(x) = F'(x) = \frac{3}{4} (1+x)(1-2x)$$\)

iii. Evaluating\(P(-0.2 < X <0.2):$$P(-0.2 < X <0.2) = F(0.2) - F(-0.2)$$$$P(-0.2 < X <0.2) = \int_{-0.2}^{0.2} f(x) dx$$$$P(-0.2 < X <0.2) = \int_{-0.2}^{0.2} \frac{3}{4} (1+x)(1-2x) dx$$$$P(-0.2 < X <0.2) = 0.0576$$\)

To know more about probability visit:

https://brainly.com/question/31828911

#SPJ11

Answer:

x + 2y = 13}(add the both eqns)

-x + y = 5}

x +(-x) = 0

2y + y = 3y

13 + 5 = 18

then,

3y = 18

y = 6

from

x + 2y = 13

x = 13 - 2(6)

x = 1

Answer:

B) x = √118 mi

Step-by-step explanation:

This is a right triangle, so we can the measure of x using the Pythagorean theorem, which is

a^2 + b^2 = c^2, where

Step 1:  Plug in x and √26 for a and b and 12 for c and simplify:

x^2 + (√26)^2 = 12^2

x^2 + 26 = 144

Step 2:  Subtract 26 from both sides to isolate x^2:

(x^2 + 26 = 144) - 26

x^2 = 118

Step 3:  Take the square root of both sides to isolate x:

√(x^2) = √118

x = √118 mi

Positive divisors does n2 have are 5.

If an integer n has exactly three positive divisors, including 1 and n, it means that n is a perfect square of a prime number.

The reason for this is that a prime number has only two divisors: 1 and itself. Therefore, if n has exactly three positive divisors, n must be a perfect square of a prime number, since the only divisors of a perfect square are the divisors of its square root, and its square root must be a prime number.

Let's say that n is equal to p², where p is a prime number. The positive divisors of n are 1, p, and n (which is p²).

Now, to find the number of positive divisors of n², we can use the fact that any positive divisor of n² can be expressed in the form \(p^k\), where 0 ≤ k ≤ 4 (since n² = p⁴).

Therefore, the positive divisors of n² are:

1, p, p², p³, and p⁴ (which is n²)

So, n² has 5 positive divisors: 1, p, p², p³, and n².

Hence, the answer is 5.

Learn more about positive divisors.

brainly.com/question/30207836

#SPJ11

The probability that in a given ten-minute interval, 15 cars arrive at the booth, and 10 of these are japanese imports = 0.0002

We know that the conditions for the Poisson distribution.

1) The occurrence of one event does not affect the probability another event will occur. i.e., the events are independent events.

2) The average rate i.e., the ratio events per time period is constant.

3) Two events cannot occur at the same time.

and the formula for the Poisson distribution is:

\(P(X = k)=\frac{e^{-\lambda}\times {\lambda}^k}{k!}\)

Here, the cars arrive at a toll booth according to a Poisson process at a rate of 3 arrivals per minute.

We need to find the probability tthat in a given ten-minute interval, 15 cars arrive at the booth, and 10 of these are japanese imports.

Here, we need to multiply the Binomial probability of 10 out of 15 cars being Japanese with the Poisson probability of 15 cars arriving in a 10 minute period.

The Binomial probability of 10 out of 15 cars would be:

P₁(x = 10) = ¹⁵C₁₀ (0.6)¹⁰ (0.4)¹⁵⁻¹⁰

P₁ = 0.18594

And the Poisson probability of 15 cars arriving in a 10 minute period.

So we use λ = 30.

P₂(X = 15) = \(\frac{e^{-30}\times {30}^{15}}{15!}\)

P₂ = 0.0010

So, the required probability would be:

P = P₁ × P₂

P =  0.18594 ×  0.001

P = 0.00018594

P= 0.0002

Therefore, the required probability is 0.0002

Learn more about the probability here:

brainly.com/question/15124899

#SPJ4

The complete question is:

Cars arrive at a toll booth according to a Poisson process at a rate of 3 arrivals per minute.

b) Of the cars arriving at the both, it is known that over the long run 60% are Japanese imports. What is the probability that in a given ten-minute interval. 15 cars arrive at the booth, and 10 of these are Japanese imports? State your assumptions clearly.

Consider the below below figure is attached with this question.

Given:

M is the midpoint of LN.

N is the midpoint of MO.

To prove:

LM=NO​ (instead of LM=MO).

Solution:

It is given that, M is the midpoint of LN. So,

\(LM=MN\)             ...(i)

N is the midpoint of MO. So,

\(MN=NO\)             ...(ii)

Using (i) and (ii), we get

\(LM=NO\)

Hence proved.

(a) Mathematically, this can be expressed as: MRS = p1/p2, where MRS is the marginal rate of substitution and p1/p2 is the price ratio of the two goods. (b) This condition ensures that the consumer would not be willing to trade more units of the second good for the first good at the given prices, as it would violate the optimality condition for utility maximization.

(a) To show that the indifference curve through an interior solution, denoted as x*, must be tangent to the consumer's budget line, we can use the concept of marginal rate of substitution (MRS) and the slope of the budget line.

The MRS measures the rate at which a consumer is willing to trade one good for another while remaining on the same indifference curve. It represents the slope of the indifference curve.

The budget line represents the combinations of goods that the consumer can afford given their income and prices. Its slope is determined by the price ratio of the two goods.

If x* is an interior solution, it means that the consumer is consuming positive amounts of both goods. At x*, the MRS must be equal to the price ratio for the consumer to be in equilibrium.

Mathematically, this can be expressed as:

MRS = p1/p2

where MRS is the marginal rate of substitution and p1/p2 is the price ratio of the two goods.

(b) If x* ∈ \(R+^2\)and x1* = 0, it means that the consumer is consuming only the second good and not consuming any units of the first good.

In this case, the marginal utility of the second good (MU2) divided by the marginal utility of the first good (MU1) should be less than the price ratio of the two goods (p2/p1) for the consumer to be in equilibrium.

Mathematically, this can be expressed as:

MU2/MU1 < p2/p1

This condition ensures that the consumer would not be willing to trade more units of the second good for the first good at the given prices, as it would violate the optimality condition for utility maximization.

Learn more about indifference curve here:

https://brainly.com/question/32705949

#SPJ11

Is the ratio 15:12 equivalent to these? No, it's not equivalent.

Why not? Because if we tripled everything in 5:3 then we'd get 15:9. We don't have the second value as 12.

-------------------------------------

Is the ratio 30:18 equivalent to these? Yes it is equivalent

To go from 5:3 to 30:18, we multiply everything by 6

5*6 = 30

3*6 = 18

This shows that 5:3 scales up to 30:18

-------------------------------------

Give two more examples of ratios that are equivalent to 5:3.

Pick any number you want. Let's say we pick 7. Multiply both parts of 5:3 by the value 7

5*7 = 35

3*7 = 21

The ratio 5:3 is equivalent to 35:21

The ratio 5:3 is also equivalent to 50:30 after multiplying both parts by 10.

The mass of a cubic meter of air at room temperature (20°C) depends on various factors such as atmospheric pressure and humidity. However, as a rough estimate, at standard atmospheric conditions, the mass of dry air in a cubic meter is approximately 1.2 kilograms.

What is cubic meter?

A cubic meter is a unit of volume in the metric system. It represents the amount of space occupied by a cube that measures one meter on each side. It is commonly used to measure the volume of solids, liquids, or gases.

The mass of air can be calculated by considering its density. At standard atmospheric pressure (101.325 kilopascals) and temperature (20°C), the approximate density of dry air is about 1.2 kilograms per cubic meter. This value may vary depending on factors such as altitude, humidity, and temperature deviations from the standard conditions.

It's worth noting that including water vapor in the air would increase the mass further. Therefore, the given estimate of 1.2 kilograms represents the mass of dry air, neglecting the presence of water vapor.

To know more about room temperature, refer here:

https://brainly.com/question/964800

#SPJ4

Answer:

y = -2

Step-by-step explanation:

y-intercept is the point of y at which x is zero

so it is (0,-2) when y= -2

Hope it helps!

Answer:

66, 114, 114

Step-by-step explanation:

angle 3=angle 1=66

angle 2=angle 4=180- angle 3=114

A table that displays the number of individuals who fall into each combination of categorical variables is called a contingency table.

Contingency tables, also known as cross-tabulation tables or crosstabs, are a useful tool for analyzing the relationship between two or more categorical variables.

In a contingency table, each row represents a category of one variable, and each column represents a category of another variable. The intersections of the rows and columns, called cells, display the count or frequency of observations that fall into the specific combination of categories. This allows researchers to identify patterns, trends, and possible associations between the variables being studied.

One common application of contingency tables is in hypothesis testing, particularly the chi-square test of independence. This test evaluates whether there is a significant association between the categorical variables, or if the observed frequencies are simply due to chance.

In conclusion, a contingency table is a valuable tool for organizing and analyzing categorical data, enabling researchers to identify patterns and relationships among variables and aiding in the decision-making process.

Know more about   hypothesis    here:

https://brainly.com/question/29576929

#SPJ11

The probability that at least one household has their TV set tuned to the game is 1 - (1-0.22)^33, which is approximately 0.993.

To solve this problem using the direct method, we can use the fact that 22% of TV sets were tuned to the game. This means that the probability of a randomly selected TV set being tuned to the game is 0.22.

To find the probability that at least one of the 33 households surveyed had their TV set tuned to the game, we can use the complement method. The complement of the event "at least one household has their TV set tuned to the game" is "none of the households have their TV set tuned to the game".

Using the complement method, we can find the probability of this event by taking the probability that no households have their TV set tuned to the game, which is (1-0.22)^33.

So, the probability that at least one household has their TV set tuned to the game is 1 - (1-0.22)^33, which is approximately 0.993.

If I had to do this by hand, I would use the complement method, as it involves simpler calculations.

To find the probability that at least one TV set among the 33 households surveyed is tuned to NBC Sunday Night Football, we can use either the direct method or the complement method.

1. Direct Method:
The direct method requires calculating the probabilities of 1, 2, 3, ..., 33 households watching the game, and then summing up these probabilities. This method can be tedious and time-consuming, especially when done by hand.

2. Complement Method:
The complement method is generally easier and quicker, as it involves calculating the probability that none of the 33 households is watching the game and then subtracting this probability from 1.

Given that 22% (0.22) of the TV sets in use were tuned to the game, the probability that a household is not watching the game is 1 - 0.22 = 0.78.

For all 33 households not to be watching the game, the probability is (0.78)^33 ≈ 0.00038.

Now, to find the probability that at least one household is watching the game, we subtract this probability from 1:

1 - 0.00038 ≈ 0.99962.

So, the probability that at least one of the 33 households is tuned to NBC Sunday Night Football is approximately 0.99962.

If you had to do this by hand, the complement method would be the preferred approach, as it requires fewer calculations and is more straightforward.

Learn more about probability at: brainly.com/question/30034780

#SPJ11