What ratio is equivalent to 3 to 8
Answers
Answer:
6 to 16
Step-by-step explanation:
There are a lot of equivalent equations but you can't simplify 3 to 8.
Answer:
If you were to multiply both by 2 you would get a new ratio: 6 to 16
Step-by-step explanation:
As long as you multiply both 3 and 8 by the same number you will get a ratio that is equal to 3:8
Hope this helps!
Related Questions
A bouncy ball is dropped such that the height of its first bounce is 4.5 feet and each successive bounce is 73% of the previous bounce's height. What would be the height of the 10th bounce of the ball? Round to the nearest tenth (if necessary).
Answers
The height of the 10th bounce of the ball will be 0.6 feet.
What is geometric sequence?A geometric sequence is a sequence in which each term is found by multiplying the preceding term by the same value.
What is the formula for finding the nth term of geometric sequence?The nth term of the geometric sequence is given by
\(\sf T_n=ar^{n-1}\)
Where,
\(\sf T_n\) is the nth term.r is the common ratioa is the first termAccording to the given question.
During the first bounce, height of the ball from the ground, a = 4.5 feet
And, the each successive bounce is 73% of the previous bounce's height.
So,
During the second bounce, the height of ball from the ground
\(\sf = 73\% \ of \ 10\)
\(=\dfrac{73}{100}(10)\)
\(\sf = 0.73 \times 10\)
\(\sf = 7.3 \ feet\)
During the third bounce, the height of ball from the ground
\(\sf = 73\% \ of \ 7.3\)
\(=\dfrac{73}{100}(7.3)\)
\(\sf = 5.33 \ feet\)
Like this we will obtain a geometric sequence 7.3, 5.33, 3.11, 2.23,...
And the common ratio of the geometric sequence is 0.73
Therefore,
The sixth term of the geometric sequence is given by
\(\sf T_{10}=10(0.73)^{10-1\)
\(\sf T_{10}=10(0.73)^{9\)
\(\sf T_{10}=10(0.059)\)
\(\sf T_{10}=0.59\thickapprox0.6 \ feet\)
Hence, the height of the 10th bounce of the ball will be 0.6 feet.
Find out more information about geometric sequence here:
brainly.com/question/11266123
you have 20 boxes of hats, of four different colors. what is the worst case number of boxes you'll have to open to get 5 of the same color?
Answers
To find the worst-case number of boxes you will have to open to get 5 boxes of the same color from 20 boxes of hats of four different colors, we can use the pigeonhole principle.The pigeonhole principle states that if there are n pigeonholes and more than n pigeons, then there must be at least one pigeonhole with at least two pigeons.
In other words, if there are more items than containers to put them in, then at least one container must have more than one item.In this case, we have 20 boxes and 4 different colors. Without loss of generality, we can assume that we have 5 boxes of each color. So, we can think of this as having 5 pigeonholes (one for each color) and 20 pigeons (one for each box).
We want to find the worst-case scenario for getting 5 boxes of the same color, so we want to minimize the number of boxes we have to open. To do this, we want to maximize the number of boxes we can eliminate with each opening. The best strategy is to open a box of each color at each step. That way, we can eliminate 4 boxes with each step and we can be sure that we won't miss any colors if we get to step 5 without finding 5 boxes of the same color.
The worst-case scenario is when we have opened 16 boxes and still haven't found 5 boxes of the same color. At that point, we must have at least 4 boxes of each color left, and we can eliminate at most 3 of them with each step. So, we need at least 2 more steps to find 5 boxes of the same color. Therefore, the worst-case number of boxes we'll have to open is 16 + 2 × 3 = 22.
To know more about color visit:
https://brainly.com/question/32142070
#SPJ11
the concession stand at a football game sells hot dogs and drinks. 2 22 hot dogs and 4 44 drinks cost $ 8 $8dollar sign, 8. it costs $ 7 $7dollar sign, 7 for 3 33 hot dogs and 2 22 drinks. what is the cost for 1 11 hot dog and 1 11 drink?
Answers
As per the given equation, the cost for one hot dog and one drink is $2.75.
Let's begin by setting up some equations. Let H be the cost of one hot dog and D be the cost of one drink. We can use the information given in the problem to create two equations:
2H + 4D = 8 (equation 1)
3H + 2D = 7 (equation 2)
Equation 1 represents the cost of 2 hot dogs and 4 drinks, which is equal to $8. Equation 2 represents the cost of 3 hot dogs and 2 drinks, which is equal to $7.
To solve for H and D, we can use algebraic techniques such as substitution or elimination. Let's use substitution by solving equation 2 for D in terms of H:
2D = 7 - 3H
D = (7/2) - (3/2)H
Now we can substitute this expression for D into equation 1 and solve for H:
2H + 4[(7/2) - (3/2)H] = 8
2H + 14 - 6H = 8
-4H = -6
H = 3/2
We have found that one hot dog costs $1.50. To find the cost of one drink, we can substitute H = 3/2 into equation 2 and solve for D:
3(3/2) + 2D = 7
9/2 + 2D = 7
2D = 5/2
D = 5/4
We have found that one drink costs $1.25.
Then the cost for one hot dog and one drink is calculated as,
=> $1.50 + $1.25 = $2.75.
To know more about equation here
https://brainly.com/question/10413253
#SPJ4
The weights of three children are in the properation 6:5:4 If the weight of the smallest chill is 25 Kg. find the weights of the other 2 Children.
Answers
The weight of the other children are 37.5 kg and 31.25 kg
How to calculate the weight of the other children?
The weight of the three children are 6:5:4
6x, 5x and 4x
The weight of the smallest child is 4x
4x= 25
x= 6.25
The weight of the other two children can be calculated as follows
6(6.25)
= 37.5
5(6.25)
= 31.25
Hence the weight of the other two children are 37.5 kg and 31.25 kg
Read more on weight here
https://brainly.com/question/17046502
#SPJ1
In the equation z = ct d, z is measured in meters and t is measured in seconds. what are the dimensions (units) of c?
Answers
In the equation z = c t + d, where z is measured in meters (m) and t is measured in seconds (s), the dimensions of c are meters/seconds or m / s
Given: The equation z = c t + d, where z is measured in meters and t is measured in seconds. To find the dimensions of c
What are the units and dimensions?
Dimensions can be defined as some physical quantities that exist in some particular domains of existence that can be measured, whereas units are just some arbitrary names that are reserved by particular dimensions which are used to define the quantity that is about the measurement or the dimensions used concerning the particular object or instance of something.
What is the homogeneity of dimensions?
In a given equation consisting of different variables, the dimensions assigned with each term in the equation must be consistent on both the left and right sides.
For example: Let's take the formula of final velocity (v):
v = u + a t, where
v = final velocity and unit is m / s
u = initial velocity and unit is m / s
a = linear acceleration and unit is m / s²
t = time and unit is t
Observe the dimension and units for each term in the equation.
On the left-hand side, we have only one term which is v (final velocity) and is measured in m / s.
On the right-hand-side, we have 2 terms u (initial velocity) and at (acceleration and time)
u is measured in m / s
a is measured in m / s² and t is measured in s
so, it is measured in m / s² × s is m / s
Therefore both u and at has the dimensions as m / s.
Hence all the terms in LHS and RHS which are v, u, and at are measured in m / s.
This is known as the homogeneity of dimensions for an equation.
Let's solve the given equation:
z = c t + d
where z is measured in meters and t is measured in seconds.
Now z is measured in meters (m), so by the principle of homogeneity of dimensions, c t must also be measured in meters (m).
Now t is measured in seconds (s), so if the dimensions of c are meters/second then the term c t will be measured in meters.
Hence the dimensions of c are meters/second or m / s
Know more about "dimensions" here: https://brainly.com/question/13770353
#SPJ4
In the equation z = c t + d, where z is measured in meters (m) and t is measured in seconds (s), the dimensions of c are meters / seconds which can also be expressed as m / s.
We are given the equation z = c t + d;
where z is measured in meters and t is measured in seconds. T
We have to find the dimension or units of c.
Dimensions means some physical quantities that exist in some particular domains of existence and can be measured.
If we have a equation, then the dimension that is on the left sides of it should be the same as the one on the right on it.
This is called the homogeneity of dimensions for an equation that is being given.
Now, we have the equation:
z = c t + d
Since,
z is being measured in meters (m), so by using the principle of homogeneity of dimensions, c t must also be measured in meters (m).
Also, t is measured in seconds (s).
So, if the dimensions of c are meters/second then the term c t will be measured in meters.
Therefore, the dimensions of c are meters/second or m / s.
Learn more about "dimensions" here:
brainly.com/question/13770353
#SPJ4
someone please help

Answers
Answer:
sqrt(106) =c
Step-by-step explanation:
Since this is a right triangle, we can use the Pythagorean theorem
a^2+b^2 = c^2 where a and b are the legs and c is the hypotenuse
5^2 +9^2 = c^2
25+81 = c^2
106 = c^2
Taking the square root of each side
sqrt(106)= sqrt(c^2)
sqrt(106) =c
Answer:
Length of missing side is 10.44/ √106.
Step-by-step explanation:
Here we have
A right triangle with
1st side = a = 5
2nd sidd = b = 9
and , we need to find 3rd side of triangle
let the 3rd side be x.
Using Pythagoras theorem
a ² + b ² = c ²
( 5 ) ² + ( 9 ) ² = ( c)²
25 + 81 = ( c) ²
106 = ( c) ²
Taking square root of each side
√106 = √ c ²
√106 = c
10.44 = c
So, missing side if triangle is 10.44 /√106.
I need this answer ASAP

Answers
Answer:
166m
Step-by-step explanation:
To calculate the area you multiply the length of all the pieces and add them to get. 4x5=20 then double that because there is 2 of those pieces and do the same for the rest of them. After all the multiplying you should get 40, 70, and 56 add them all up to get the answer
Solve following proportion. (2.2)/x = 26.4/96
Answers
Proportion refers to the relationship between two or more quantities, indicating how they are related or compared to each other. It involves comparing the relative sizes or amounts of different elements or parts within a whole or between different entities.
To solve the proportion (2.2)/x = 26.4/96, we can cross multiply.
First, cross multiply by multiplying the numerator of the first fraction (2.2) with the denominator of the second fraction (96).
(2.2) * (96) = 211.2
Next, cross multiply by multiplying the denominator of the first fraction (x) with the numerator of the second fraction (26.4).
(x) * (26.4) = 26.4x
Now, set the two cross products equal to each other:
211.2 = 26.4x
To isolate x, divide both sides of the equation by 26.4:
211.2 / 26.4 = x
Simplifying the division gives us:
x ≈ 8
Therefore, the value of x that solves the proportion is approximately 8.
To know more about Proportion visit:
https://brainly.com/question/33460130
#SPJ11
The Garraty Company has two bond issues outstanding. Both bonds pay $100 annual interest plus $1,000 at maturity. Bond L has a maturity 15 years, and Bond S has a maturity of 1 year. a. made on Bond S. Do not round intermediate calculations. Round your answers to the nearest cent. Bond L: $ Bond S: $ made on Bond S. Do not round intermediate calculations. Round your answers to the nearest cent. Bond L: $ Bond S: \$ made on Bond S. Do not round intermediate calculations. Round your answers to the nearest cent. Bond L: \$ Bond S: \$ b. Why does the longer-term (15-year) bond fluctuate more when interest rates change than does the shorter-term bond (1 year)? I. Longer-term bonds have less interest rate risk than shorter-term bonds. II. Longer-term bonds have less reinvestment rate risk than shorter-term bonds. III. Longer-term bonds have more interest rate risk than shorter-term bonds.
Answers
Statement I is correct, while statements II and III are false. The longer-term bond (Bond L) fluctuates more due to its higher interest rate risk compared to the shorter-term bond (Bond S).
To calculate the value of Bond L and Bond S, we need more information, specifically the interest rate or yield associated with these bonds.
a. Bond prices are influenced by various factors, including the bond's face value, coupon payments, time to maturity, and prevailing interest rates. Without the interest rate or yield, we cannot determine the exact values of Bond L and Bond S.
The bond price can be calculated using the present value formula, which discounts the future cash flows of the bond to their present value.
b. The longer-term bond (Bond L) tends to fluctuate more when interest rates change compared to the shorter-term bond (Bond S) due to interest rate risk. Interest rate risk refers to the impact of changes in interest rates on the value of a bond.
I. Longer-term bonds have more interest rate risk than shorter-term bonds. This statement is true. Longer-term bonds are exposed to changes in interest rates for a more extended period, which makes their prices more sensitive to interest rate movements. When interest rates rise, the value of longer-term bonds tends to decrease more than shorter-term bonds.
II. Longer-term bonds have less reinvestment rate risk than shorter-term bonds. This statement is false. Reinvestment rate risk refers to the risk of reinvesting coupon payments at lower interest rates when the bond matures. Longer-term bonds have a higher reinvestment rate risk because they have more coupon payments to reinvest over the bond's longer lifespan.
III. Longer-term bonds have less interest rate risk than shorter-term bonds. This statement is false. As mentioned earlier, longer-term bonds have more interest rate risk because their prices are more sensitive to changes in interest rates compared to shorter-term bonds.
In summary, statement I is correct, while statements II and III are false. The longer-term bond (Bond L) fluctuates more due to its higher interest rate risk compared to the shorter-term bond (Bond S).
Learn More About longer-term bond from the below link:
https://brainly.com/question/9795298
#SPJ11
what is the relationship between the singular values of a and the eigen- values of aat ? what about at a?
Answers
The eigenvectors of AAH are called the left-singular vectors of A and the eigenvectors of AHA are the right-singular vectors of A . They are called this way because of their use in singular value decomposition. Say A=UΣVH , then the columns of U are the left-singular vectors and the columns of V are right-singular vectors.
We know that the non-zero eigenvalues of AAH and AHA are the same, they are the squares of the singular values of A . A singular of value of A is a value σ such that Av=σu AHu=σv where u is a left-singular vector and vs a right-singular vector. This can be taken as the definition of singular value, left-singular vector (which is an eigenvector of AAH) and right-singular vector (which is an eigenvector of AHA).the left-singular and right-singular vector pair works with AAH and AHA
AAHu=σAv=σ2u
AHAv=σAHu=σ2v
To learn more about eigenvectors visit:
brainly.com/question/29658558
#SPJ4
Q: What is the relationship between the eigenvectors of AAT and ATA?
1. Jesse estimates that it will cost $300,000 to send his newborn son to a private college
in 18 years. He currently has $65,000 to deposit in an account.
a. What simple interest rate would he need so that $65,000 grows into $300,000
in 18 years? Round to the nearest percent. 20%
b. How much would the account earn in three years if the interest was
compounded yearly?
I
C. Look at the table below showing activity for five months. Fill in the missing
information showing the account compounded monthly.
Answers
Jesse would need a simple interest rate of 20.09% so that $ 65,000 grows into $ 300,000 in 18 years. In turn, if the interest was compounded yearly, the account would earn $ 47,572.90 in three years.
Given that Jesse estimates that it will cost $ 300,000 to send his newborn son to a private college in 18 years, and he currently has $ 65,000 to deposit in an account, to determine what simple interest rate would he need so that $ 65,000 grows into $ 300,000 in 18 years, and how much would the account earn in three years if the interest was compounded yearly, the following calculations must be performed:
65,000X = 300,000 X = 300,000 / 65,000 X = 4.6154 (4.6154 - 1) / 18 = X 0.20085 = X 0.20085 x 100 = 20.0855
Therefore, he would need a simple interest rate of 20.09% so that $ 65,000 grows into $ 300,000 in 18 years.
65,000 x 1,2009 x 1,2009 x 1,2009 = X 78,058.5 x 1.2009 x 1.2009 = X 93,740.45 x 1.2009 = X 112,572.90 = X 112,572.90 - 65,000 = 47,572.90
Therefore, if the interest was compounded yearly, the account would earn $ 47,572.90 in three years.
Learn more in https://brainly.com/question/14295570
G
The point-slope form of the equation of a line that passes through points (8, 4) and (0, 2) is y-4=1/4(x-8). What is
the slope-intercept form of the equation for this line?
Oy=-1/4x-12
y=1/4-x-4
○ y =1/4 x+2
○y=1/4x+6
Mark this and return
Save and Exit
Next
Submit
Answers
The point-slope form of the equation of a line that passes through points (8, 4) and (0, 2) is y-4=1/4(x-8). The slope-intercept form of the equation for this line is y = x/4 + 2.
The equation of the line in the point-slope form :
y - b = m(x - a)
where m is the slope and (a,b) are the points on the line.
y - 4 = (x - 8)/4
Here, m = 1/4 and (a,b) = (8,4)
The equation of the line in slope-intercept form:
y = mx +c
y = x/4 + c
To find c, putting (8,4) into the above equation,
4 = 2 + c
c = 2
Therefore, y = x/4 + 2 is the slope-intercept form.
What is the intercept?
The point where the line or curve crosses the axis of the graph is called the intercept. If a point crosses the x-axis, then it is called the x-intercept. If a point crosses the y-axis, then it is called the y-intercept.An intercept in mathematics is a location on the y-axis through which the line's slope passes. It is a place on the y-axis where a straight line or a curve crosses. This is reflected in the equation for a line, which is written as y = mx+c, where m denotes slope and c denotes the y-intercept.X-intercept and Y-intercept are the two main intercepts. The line's x-intercept and y-intercept are located where the line crosses the x and y axes, respectively.To learn more about intercept, visit: https://brainly.com/question/13619672
#SPJ1
Consider the function f(x,y,z)=5+yxz+g(x,z) where g is a real-valued differentiable function. Find the directional derivative of f at the point (3,0,3) along the direction of the vector (0,4,0). Enter your answer symbolically, as in these
Answers
Given, the function is f(x,y,z)=5+yxz+g(x,z)Here, we need to find the directional derivative of f at the point (3,0,3) along the direction of the vector (0,4,0) . The directional derivative of f at the point (3,0,3) along the direction of the vector (0,4,0) is 0.
Using the formula of the directional derivative, the directional derivative of f at the point (3,0,3) along the direction of the vector (0,4,0) is given by
(f(x,y,z)) = grad(f(x,y,z)).v
where grad(f(x,y,z)) is the gradient of the function f(x,y,z) and v is the direction vector.
∴ grad(f(x,y,z)) = (fx, fy, fz)
= (∂f/∂x, ∂f/∂y, ∂f/∂z)
Hence, fx = ∂f/∂x = 0 + yzg′(x,z)fy
= ∂f/∂y
= xz and
fz = ∂f/∂z = yx + g′(x,z)
We need to evaluate the gradient at the point (3,0,3), then
we have:fx(3,0,3) = yzg′(3,3)fy(3,0,3)
= 3(0) = 0fz(3,0,3)
= 0 + g′(3,3)
= g′(3,3)
Therefore, grad(f(x,y,z))(3,0,3) = (0, 0, g′(3,3))Dv(f(x,y,z))(3,0,3)
= grad(f(x,y,z))(3,0,3)⋅v
where, v = (0,4,0)Thus, Dv(f(x,y,z))(3,0,3) = (0, 0, g′(3,3))⋅(0,4,0) = 0
The directional derivative of f at the point (3,0,3) along the direction of the vector (0,4,0) is 0.
Learn more about Derivative:
https://brainly.com/question/32963989
#SPJ11
Larry and Carol are both members of a population, and a simple random sample is being conducted. If the chance of Larry being selected is 1/800, what is the chance of Carol being selected
Answers
By simple reasoning, The chance of Carol being selected is 1/800.
What in probability is a random process?A collection of random variables, typically indexed by time, makes up a random process. Here, the process S(t) is an illustration of a continuous-time random process. In general, a random process X(t) is a continuous-time random process if t can take real values in an interval on the real line.
A straightforward random sample is being taken from a population that includes both Larry and Carol.
So both of them have an equal chance of being chosen.
Now, Larry's likelihood of being chosen is 1 in 800.
The likelihood of Carol being chosen is then 1 in 800.
To know more about probability visit:-
brainly.com/question/11234923
#SPJ4
let a and b be n × n matrices such that ab = in . prove that the rank of a is n
Answers
The rank of matrix A is n.
To prove that the rank of matrix A is n, we'll use the facts that AB = I_n (the n x n identity matrix) and that the rank of a product of matrices is less than or equal to the minimum of the ranks of the individual matrices. Here's a step-by-step explanation:
1. Given: A and B are n x n matrices such that AB = I_n.
2. Let's denote the rank of A as rank(A) and the rank of B as rank(B).
3. Since AB = I_n, it's clear that the product of matrices A and B results in the identity matrix, which has a rank of n (rank(I_n) = n).
4. According to the properties of matrix ranks, rank(AB) ≤ min(rank(A), rank(B)).
5. As AB = I_n, we have rank(I_n) ≤ min(rank(A), rank(B)).
6. Since the rank of the identity matrix is n, we have n ≤ min(rank(A), rank(B)).
7. As A and B are n x n matrices, their maximum possible rank is n, so rank(A) ≤ n and rank(B) ≤ n.
8. From step 6, we know that n ≤ rank(A). Combining this with rank(A) ≤ n, we conclude that rank(A) = n.
Therefore, the rank of matrix A is n.
Learn more about rank of matrix here: brainly.com/question/29811883
#SPJ11
Solve the following systems of equations using Gaussian Elimination. 2x + 3y + z = 2 y + 5z = 20 -x+2y+3z = 13
Find the inner product of two vectors A = (2, -3,0) and B = = (-1,0,5)
Answers
The inner product of two vectors A = (2, -3,0) and B = (-1,0,5) is -2 / √(13×26).
Solving the given system of equations using Gaussian elimination:
2x + 3y + z = 2 y + 5z = 20 -x+2y+3z = 13
Matrix form of the system is
[A] = [B] 2 3 1 | 2 0 5 | 20 -1 2 3 | 13
Divide row 1 by 2 and replace row 1 by the new row 1: 1 3/2 1/2 | 1
Divide row 2 by 5 and replace row 2 by the new row 2: 0 1 1 | 4
Divide row 3 by -1 and replace row 3 by the new row 3: 0 0 1 | 5
Back substitution, replace z = 5 into second equation to solve for y, y + 5(5) = 20 y = -5
Back substitution, replace z = 5 and y = -5 into the first equation to solve for x, 2x + 3(-5) + 5 = 2 2x - 15 + 5 = 2 2x = 12 x = 6
The solution is (x,y,z) = (6,-5,5)
Therefore, the solution to the given system of equations using Gaussian elimination is (x,y,z) = (6,-5,5).
The given two vectors are A = (2, -3,0) and B = = (-1,0,5). The inner product of two vectors A and B is given by
A·B = |A||B|cosθ
Given,A = (2, -3,0) and B = (-1,0,5)
Magnitude of A is |A| = √(2²+(-3)²+0²) = √13
Magnitude of B is |B| = √((-1)²+0²+5²) = √26
Dot product of A and B is A·B = 2(-1) + (-3)(0) + 0(5) = -2
Cosine of the angle between A and B is
cosθ = A·B / (|A||B|)
cosθ = -2 / (√13×√26)
cosθ = -2 / √(13×26)
Learn more about equation at
https://brainly.com/question/12998758
#SPJ11
PLS HELP ME
Given that the universal set.
U = {X : 30 ≤ X ≤ 40. X is an even number}.
P = {X : X is a multiple of 4}
and Q = {X : X is a number such that the sum of its digits is an odd number}.
find n(P∩Q')
A. 1
B. 2
C. 3
D. None of the above
Answers
Given that
U = {X : 30 ≤ X ≤ 40. X is an even number}.
so Mathematically
U = {30,32,34,36,38 40}.
P = {X : X is a multiple of 4}
P = { 4,8,12,16,20,24,28,32,36,40,44,........}
and Q = {X : X is a number such that the sum of its digits is an odd number}.
Q = {12,14,16,18,21,23,25,27,29,30,32,34,36,38,41,43,45,..........}.
(Q')= U-Q ={40}
(P∩Q')= {40}
n(P∩Q')= 1
(Q') is Q complement which means a set containing those elements of the universal set which are not element of the set Q.
(P∩Q') is a set containing those elements of set P and Q complement which are common to both sets.
n(P∩Q') denotes the number of elements in a set containing those elements of set P and Q complement which are common to both sets which has only 1 element which is 40.
So the best answer is part A = 1.
https://brainly.com/question/11439790
https://brainly.com/question/13729460
a number m is more than -7
Answers
Answer:
m >-7
Step-by-step explanation:
Answer:
\(m>-7\)
Step-by-step explanation:
This is an equation that shows a number m is more than -7.
1945 men and 2849 women regiter to audition for a inging competition. The number of participant who are not ucceful in their audition what’ five time the number of thoe who are ucceful. How many participant were ucceful
Answers
1945 men and 2849 women register to audition for a singing competition. The number of participants who are not successful in their auditions what’s five times the number of those who are successful. There are 799 participants were successful.
The successful participants can be calculate by solving a linear equation as follows
First, it's crucial to understand linear equations.
Equation connects the two algebraic expressions with an equal to sign to demonstrate the equality between the two algebraic expressions.
Linear equations are those with one degree.
In this case, a linear equation must be resolved.
1945 for the men's total
Women are present in 2849.
Participants in total: 1945 + 2849 = 4794
Let x be the proportion of participants that were successful.
Men who failed were 5 times as numerous.
Participants in total: 5x + x = 6x
Due to the issue,
The linear formula is
6x = 4794
x = 4794/6
x = 799
799 of the participants had success.
To learn more about linear equation, refer to the link-
brainly.com/question/2030026
#SPJ4
answer quick please!!
Match the reasons with the statements in the proof to prove AB || DC, given that AD is parallel to BC and AD = CB.
Given:
AD || BC
AD = CB
Prove:
AB || DC
1. AD || BC, AD = CB
Reflexive Property of Equality
2. AC = AC
Given
3. 2 = 3
If Alternate Interior Angles are Congruent, then Lines are Parallel.
4. ACD = CAB
If Lines are Parallel, then Alternate Interior Angles are Equal.
5. 1 = 4
SAS (Side-Angle-Side)
6. AB || DC
CPCTE (Corresponding Parts of Congruent Triangles are Equal)
onetary policy below.

Answers
AB is parallel to DC because they are equal and corresponding sides of similar triangles.
What is the reflexive property of equality?
The reflexive property of equality is a basic principle in mathematics that states that any quantity is equal to itself. In other words, if we have a variable, say "a", then a is always equal to a. Similarly, if we have an equation such as 2 + 3 = 5, we can use the reflexive property of equality to say that 5 = 5, since any quantity is equal to itself. The reflexive property is used frequently in mathematical proofs to simplify expressions and make them easier to work with.
AD || BC, AD = CB - Reflexive Property of Equality
Explanation: This reason uses the reflexive property of equality, which states that a quantity is equal to itself. In this case, the reason is stating that the given information is true and using the reflexive property of equality to restate it in a different way.
2 = 3 - If Alternate Interior Angles are Congruent, then Lines are Parallel.
Explanation: This reason uses the angle congruence property that if the alternate interior angles are congruent, then the lines are parallel. This property is used to show that angles ACD and CAB are congruent because they are alternate interior angles.
ACD = CAB - If Lines are Parallel, then Alternate Interior Angles are Equal.
Explanation: This reason uses the angle equality property that if the lines are parallel, then the alternate interior angles are equal. This property is used to show that lines AD and BC are parallel because they are given to be parallel, and therefore the alternate interior angles ACD and CAB are equal.
1 = 4 - SAS (Side-Angle-Side)
Explanation: This reason uses the similarity property that if two triangles have the same side-angle-side, then they are similar. This property is used to show that triangles ABD and CBD are similar because they have the same side AD = CB and the same angles ABD and CBD.
AB || DC - CPCTE (Corresponding Parts of Congruent Triangles are Equal)
This reason uses the CPCTE property that the corresponding parts of congruent triangles are equal. This property is used to show that sides AB and DC are equal because they are corresponding sides of similar triangles ABD and CBD. Therefore, AB is parallel to DC because they are equal and corresponding sides of similar triangles.
To know more about the reflexive property visit:
brainly.com/question/29263247
#SPJ1
Delia graphed AABC
AA'B'C'.
on the coordinate grid as shown. She applied a series of transformations which produced a simillar triangle that she labeled. What sequence of transformation did Delia use to produce triangle A’ B’C
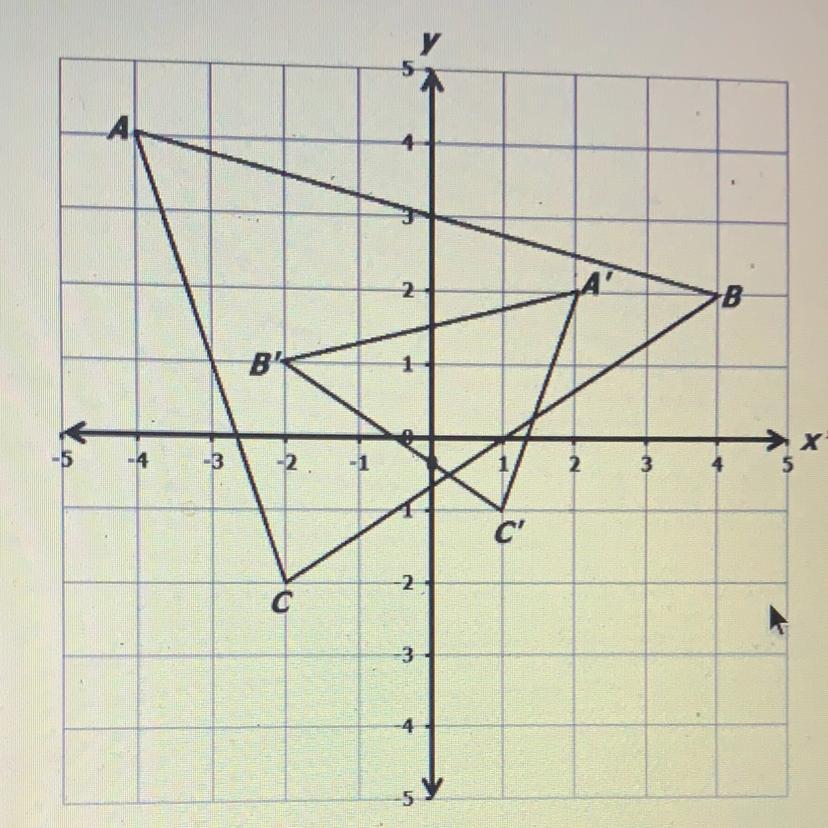
Answers
Answer:
You should watch SHREK
Step-by-step explanation:
Find the total area of the kitchen floor that is to be tiled as shown below.

Answers
Answer:
58
Step-by-step explanation:
There is two rectangles in this problem.
For the first one 5×10=50
And the second one is 2×4=8
So the final answer will be 58
Hope this helpedn
split the figure into two rectangles and find the area of each
add the two areas

1. You get a student loan from the New Mexico Educational Assistance Foundation to pay for your educational expenses this year. Find the interest on the loan if you borrowed ₱2 000 at 8% for 1 year.
Answers
Answer:
$160
Step-by-step explanation:
Step one:
given data
Principal = $2000
rate= 8%
time t= 1 year
Required
The Simple interest paid after 1 year
Step two:
Simple interest = PRT/100
Simple interest = 2000*8*1/100
Simple interest = 16000/100
Simple interest =$160
The simple interest paid after 1 year is $160
a combination lock will open when the right choice of three numbers (from 1 to 30, inclusive) is selected. How many different lock combinations are possible assuming no number is repeated?
Answers
There are 24,360 different lock combinations possible when selecting three numbers from 1 to 30 without repetition.
To find the number of different lock combinations possible, we can use the concept of permutations. Since we are selecting three numbers from a set of 30 numbers without repetition, the number of combinations can be calculated as:
30P3 = 30! / (30 - 3)!
Here, "P" represents the permutation.
Calculating the permutation:
30P3 = 30! / (30 - 3)!
= 30! / 27!
= 30 × 29 × 28
= 24,360
Therefore, there are 24,360 different lock combinations possible when selecting three numbers from 1 to 30 without repetition.
To know more about repetition refer here:
https://brainly.com/question/28014744#
#SPJ11
I need to find out the points

Answers
Answer:
The roots are x = 1 and x = 3
Step-by-step explanation:
The roots of a polynomial are those x-values for which the polynomial renders zero. Therefore, you need to look at the points of the parabola that intersect the x-axis (since they correspond to y=0:
Please see attached image for the location of the two points that cross the x-axis. They are located at (1, 0) and at (3, 0), therefore, the roots of the parabola are: x = 1 and x = 3.

find an equation of the curve that passes through the point (0, 1) and whose slope at (x, y) is 5xy. (note: start your answer with y
Answers
The equation of the curve that passes through the point (0, 1) and has a slope of 5xy at any point (x, y) is y = (5/2) * x^2y + 1. This equation represents a curve where the y-coordinate is a function of the x-coordinate, satisfying the conditions.
To determine an equation of the curve that satisfies the conditions, we can integrate the slope function with respect to x to obtain the equation of the curve. Let's proceed with the calculations:
We have:
Point: (0, 1)
Slope: 5xy
We can start by integrating the slope function to find the equation of the curve:
∫(dy/dx) dx = ∫(5xy) dx
Integrating both sides:
∫dy = ∫(5xy) dx
Integrating with respect to y on the left side gives us:
y = ∫(5xy) dx
To solve this integral, we treat y as a constant and integrate with respect to x:
y = 5∫(xy) dx
Using the power rule of integration, where the integral of x^n dx is (1/(n+1)) * x^(n+1), we integrate x with respect to x and get:
y = 5 * (1/2) * x^2y + C
Applying the initial condition (0, 1), we substitute x = 0 and y = 1 into the equation to find the value of the constant C:
1 = 5 * (1/2) * (0)^2 * 1 + C
1 = C
Therefore, the equation of the curve that passes through the point (0, 1) and has a slope of 5xy at any point (x, y) is:
y = 5 * (1/2) * x^2y + 1
Simplifying further, we have:
y = (5/2) * x^2y + 1
To know more about equation of the curve refer here:
https://brainly.com/question/31467851#
#SPJ11
BRAINLIEST!!!! PLZZZZ SEE BELOW!!!

Answers
Answer:
b. 0.25
Step-by-step explanation:
40 + 120 = 160
40 / 160
Solve for the positive value of x

Answers
The positive value of x is 6
What is Indices?An index, or power, is the small floating number that appears after a number or letter.
For example, x⁵ is an exponent expression. 5 is the index or power and x is the base. There are some rules that guides Indices.
25^(2x) = 5^(x²-12)
= 5^(4x) = 5^(x²-12
4x = x²-12
x²-4x -12 = 0
x² -6x +2x -12 = 0
(x²-6x) (2x-12) = 0
x( x-6) 2( x-6) = 0
(x+2)(x-6) = 0
x+2 = 0 or x-6 = 0
x = -2 or +6
therefore the positive value of x is 6
learn more about Indices from
https://brainly.com/question/10339517
#SPJ1
HELPPPPPP ASAPPPPPP PLEASEEE

Answers
Answer:
here
Step-by-step explanation:
-3,3
2,3
3,3
4,3
I hope this helped! :D
100 POINTS!!!!!!
Determine which function has the greater rate of change, if either.
EXPLAIN YOUR ANSWER
