What products are defined for these matrices?
Drag the operation to the boxes to correctly complete the table.

Answers
Answer:
Product is defined \({}\)
(ML, MP, NM, PQ, PL, LP, MQ, LQ)
Product is not defined
(LM, PM, MN, QP, QM, NQ, QN, NL, LN, NP, PN, QL)
Step-by-step explanation:
During multiplication of matrices, the number of columns of the first matrix must be equal to the number of rows of the second matrix it is multiplying.
Therefore, we can only multiply a m×n matrix to a n×c matrix as follows;
We can only multiply (m×n)·(n×c) → Product is defined
We can not multiply (n×c)·(m×n) →∞ Product is not defined.
Related Questions
A sequence c0, c1, c2, ... is defined by letting c0 = 3 and ck = (ck–1)2 for all integers k ≥ 1. Show that cn = 32n for all integers n ≥ 0.
Answers
By the principle of mathematical induction, the statement cn = 32n is true for all integers n ≥ 0.
To show that the sequence cn = 32n for all integers n ≥ 0, we can use mathematical induction.
Step 1: Base case
Let's first verify the statement for the base case when n = 0.
c0 = 3 (given)
32n = 3^0 = 1
So, the statement holds true for the base case.
Step 2: Inductive hypothesis
Assume that the statement is true for some arbitrary positive integer k, i.e., ck = 32k.
Step 3: Inductive step
We need to show that the statement is true for the next integer, k + 1.
We know that ck+1 = (ck)^2.
Substituting the inductive hypothesis into the equation:
ck+1 = (32k)^2 = 32(2k).
By the laws of exponentiation, (32)^2 = 32*2 = 32^2 = 32(1+1) = 32(2).
Therefore, ck+1 = 32(2k) = 32(2) = 32(1+1) = 32^2 = 32(2).
So, the statement holds true for k + 1.
Know more about mathematical induction here:
https://brainly.com/question/29503103
#SPJ11
Together they swam a total of 175 laps. Swimmer B swam 25 more than twice as many laps as Swimmer A.
Answers
Answer:
75
Step-by-step explanation:
175= 25+2a
The number of laps that Swimmer A swam was 50 laps.
How to form mathematical expression from the given description?You can represent the unknown amounts by the use of variables. Follow whatever the description is and convert it one by one mathematically. For example if it is asked to increase some item by 4 , then you can add 4 in that item to increase it by 4. If something is for example, doubled, then you can multiply that thing by 2 and so on methods can be used to convert description to mathematical expressions.
Let we suppose that:
Swimmer A swam x lapsSwimmer B swam y laps.Then, according to the given data, we have:
x + y = 175 laps
y = 25 + 2x (25 more than twice of laps of A is the number of laps of B).
Thus, we get a system of two equations as:
\(x + y = 175\\y = 25 + 2x\\\)
From second equation, putting value of y in first equation, we get:
\(x + (25 + 2x) = 175\\3x + 25 = 175\\3x = 150\\\\x = \dfrac{150}{3} = 50 \: \rm laps\)
As x is the number of laps Swimmer A swam, thus, the number of laps that Swimmer A swam was 50 laps.
Learn more about solving system of linear equations here:
https://brainly.com/question/13722693
The screen on a computer monitor has a length of
15 inches and a width of 12 inches. What is the
length of the diagonal to the nearest tenth of an
inch?
A 21.3
B 19.2
C 18.1
D 20
Answers
You use the pyth.
15^2+12^2=369
Then find the square root of 392 which is 19.2
Answer: 19.2
Step-by-step explanation:
15^2+12^2=369
Then find the square root of 392 which is 19.2
The function f(x) = a^x -4 will never cross the x-axis if a is positive.
Answers
If a is positive, the function f(x) = \(a^x\) - 4 will never cross the x-axis.
1. We want to determine whether the function f(x) = \(a^x\) - 4 will intersect or cross the x-axis.
2. To find the x-intercepts, we set f(x) = 0 and solve for x. In this case, we have \(a^x\) - 4 = 0.
3. Adding 4 to both sides of the equation, we get \(a^x\) = 4.
4. If a is positive, raising a positive number to any power will always yield a positive value.
5. Therefore, there are no values of x that will make \(a^x\) equal to 4 when a is positive.
6. Since the function f(x) = \(a^x\) - 4 cannot equal zero, it will never cross the x-axis when a is positive.
7. In other words, the graph of the function will always remain above the x-axis for positive values of a.
8. However, if a is negative, then there will be values of x where \(a^x\) - 4 = 0 and the function crosses the x-axis.
9. Therefore, the statement that the function f(x) = \(a^x\) - 4 will never cross the x-axis is true only when a is positive.
For more such questions on x-axis, click on:
https://brainly.com/question/27946240
#SPJ8
It is a point that divides a segment into two congruent segments.
A.Point
B.Midpoint
C.Bisector
D.Ray​
Answers
The point that divides a segment into two congruent segments is called the midpoint. Therefore, the answer is B) midpoint.
In geometry, a midpoint is a point that divides a line segment into two equal parts. It is the point on the line segment that is equidistant from both endpoints. The midpoint is important in geometry as it can be used to construct other geometric figures, such as perpendicular bisectors, which are lines that pass through the midpoint of a line segment and are perpendicular to it. For example, if we have a line segment AB, the midpoint M is the point that is exactly halfway between A and B, such that AM = MB. This can be found by drawing a perpendicular bisector of AB, which is a line that passes through the midpoint M and is perpendicular to AB. The perpendicular bisector will intersect AB at the midpoint M. It is important to note that the midpoint is not a bisector, ray, or point on a line. A bisector is a line, segment, or ray that divides an object into two congruent parts, while a ray is a part of a line that extends infinitely in one direction. The midpoint is simply the point that divides a line segment into two equal parts, and it is denoted by a symbol, such as a small vertical line with a hat on top, or by labeling the midpoint as a letter, such as M in the example above
To learn more about congruent segments click here
brainly.com/question/29550003
#SPJ4
/_ RQT is a straight angle. what are m/_RQS and m /_ TQS?

Answers
We can find the measure of angles RQS and TQS by applying the theorem below:
The sum of angles on a straight line is 180 degrees
Given:
\(\begin{gathered} m\angle RQS=(20x+4)^0 \\ m\angle TQS=(15x+1)^0 \end{gathered}\)Applying the theorem, we have:
\((20x+4)^0+(15x+1)^0=180^0\text{ (angles on a straight line)}\)Simplifying and solving for x:
\(\begin{gathered} 20x\text{ + 4 + 15x + 1 =180} \\ \text{Collect like terms} \\ 20x\text{ + 15x + 5 =180} \\ 35x\text{ = 180-5} \\ 35x\text{ = 175} \\ Divide\text{ both sides by 35} \\ \frac{35x}{35}\text{ = }\frac{175}{35} \\ x\text{ = 5} \end{gathered}\)When we substitute the value of x , we can find the required angles.
Hence:
\(\begin{gathered} m\angle RQS=(20x+4)^0 \\ =\text{ 20}\times5\text{ + 4} \\ =\text{ 100 + 4} \\ =104^0 \end{gathered}\)Answer: measure of angle RQS = 104 degrees
\(\begin{gathered} m\angle TQS=(15x+1)^0 \\ =\text{ 15 }\times\text{ 5 + 1} \\ =\text{ 75 + 1} \\ =76^0 \end{gathered}\)Answer: measure of angle TQS = 76 degrees
what is the probability that the waiter will earn a total of less than $450 in tips when he waits on 40 parties (round answer to 4 decimal places)?
Answers
The probability that the waiter will earn less than $450 in tips when he waits on 40 parties is 0.2364. This means that there is a 23.64% chance that the waiter will make less than $450 in tips.
The probability that the waiter will earn less than $450 in tips when he waits on 40 parties can be calculated using the binomial distribution. The binomial distribution is used to calculate the probability of success in a series of independent events. In this case, the probability of success is the probability that the waiter will earn less than $450 in tips.The number of independent events, or trials, is 40, since the waiter will serve 40 parties. The probability of success for each trial is the expected average tip amount divided by the total amount of tips the waiter is trying to earn. The expected average tip amount is $11, and the total amount of tips the waiter is trying to earn is $450, so the probability of success for each trial is 0.024.Using the binomial distribution formula, the probability that the waiter will earn less than $450 in tips when he waits on 40 parties is 0.2364. This means that there is a 23.64% chance that the waiter will make less than $450 in tips.
\(p = (n! / (x! * (n-x)!) * p^x * (1-p)^(n-x))\)
where
n = 40 (number of parties)
x = 450 (desired tip amount)
p = 0.1 (probability of earning a tip of $10)
p = (40! / (450! * (40-450)!) * 0.1^450 * (1-0.1)^(40-450))
p = 0.2364
Learn more about probability here
https://brainly.com/question/30034780
#SPJ4
____Is used for examining data with more than two variables, and it includes a different vertical axis for each variable.
Answers
A Scatter plot is used for examining data with more than two variables, and it includes a different vertical axis for each variable.
What is the Scatter plot?The variables in the scatter plot made from the data are described by the independent variable, time, which is graphed along the horizontal axis. The independent variable will be time, and the dependent variable will be the number of calories provided.
When analyzing data with more than two variables, a scatter plot is used, which has a separate vertical axis for each variable.
Therefore, a scatter plot is used for examining data with more than two variables, and it includes a different vertical axis for each variable.
Learn more about the Scatter plot here:
https://brainly.com/question/1386565
#SPJ4
Brainliest! Correct! Fast!

Answers
Answer:
c or the third one
Step-by-step explanation:
Answer:
c
Step-by-step explanation:
p is inversely proportional to 3q-1. The difference in the values of p when q = 1 and q=2 respectively is 3. Find the value of p when q = 5
Answers
Step-by-step explanation:
3q - 1 = 3(1) - 1 = 2
3q -1 = 3(2)- 1= 5
10/p = 2 10/p = 5
p= 5 p= 2 (5-2=3, so 10/p is correct)
q=5, 3(5) -1 = 14
10/p = 14
p = 0.71??
helpppl me plsssss I need help

Answers
let s = {−1, 0, 2, 4, 7}. find f(s) if a) f(x) = 1. b) f(x) = 2x 1. c) f(x) = ⌈x⁄5⌉. d) f(x)= ⌊((x^2 1))⁄3⌋.
Answers
let s = {−1, 0, 2, 4, 7}. f(s) = {1}, f(s) = {-1, 1, 5, 9, 15} and f(s) = {0, 1, 2}.
Given the set s = {−1, 0, 2, 4, 7}, I will find f(s) for each of the provided functions:
a) f(x) = 1
For every x in s, f(x) is always 1.
b) f(x) = 2x + 1
Applying this function to each element of s:
f(-1) = -1
f(0) = 1
f(2) = 5
f(4) = 9
f(7) = 15
c) f(x) = ⌈x/5⌉ (the ceiling function)
Applying this function to each element of s:
f(-1) = 0
f(0) = 0
f(2) = 1
f(4) = 1
f(7) = 2
d) f(x) = ⌊((x^2 + 1))/3⌋ (the floor function)
Applying this function to each element of s:
f(-1) = 0
f(0) = 0
f(2) = 1
f(4) = 5
f(7) = 16
So, f(s) = {0, 1, 5, 16}.
Know more about functions here;
https://brainly.com/question/12431044
#SPJ11
If you have 3 quarters, 5 dimes, and 2 nickels in your
pocket, what is the probability that you will reach into your
pocket and choose a coin, keep it in your hand, then reach
in to choose another coin and both coins will be quarters?
Answers
The probability of both coins quarters will be 1/15.
What is probability?Its basic premise is that something will almost certainly happen. The percentage of favorable events to the total number of occurrences.
If you have 3 quarters, 5 dimes, and 2 nickels in your pocket.
Then the total number of the events will be
Total event = 3 + 5 + 2
Total event = 10
Then the probability that you will reach into your pocket and choose a coin, keep it in your hand, then reach in to choose another coin, and both coin's quarters will be
P = (3/10) x (2/9)
P = 1/15
Then the probability of both coins quarters will be 1/15.
More about the probability link is given below.
https://brainly.com/question/795909
#SPJ1
The harmonic series: 1+1/2+1/3+1/4+.
diverges, but when its terms are squared the resulting series converges. T or F
Answers
The statement "The harmonic series: 1+1/2+1/3+1/4+... diverges, but when its terms are squared the resulting series converges." is True.
The harmonic series is defined as the sum of the reciprocals of the natural numbers: Σ(1/n) for n = 1 to ∞. This series is known to diverge, meaning that its sum tends to infinity as more terms are added.
However, when the terms of the harmonic series are squared, we get a new series called the p-series, with p=2: Σ(1/n^2) for n = 1 to ∞. The p-series converges if p > 1, which is true for p=2. Thus, the series Σ(1/n^2) converges to a finite sum.
In conclusion, the given statement is true, as the harmonic series diverges, but its squared terms result in a convergent series.
To learn more about harmonic series go to :
https://brainly.com/question/31790923?referrer=searchResults
#SPJ11
Matti is making moonshine in the woods behind his house. He’s
selling the moonshine in two different sized bottles: 0.5 litres
and 0.7 litres. The price he asks for a 0.5 litre bottle is 8€, for
a
Answers
Based on the calculation, it appears that Matti had approximately 94 bottles of 0.5 litres and 11 bottles of 0.7 litres in the last patch of moonshine that he sold.
To solve the problem using the determinant method (Cramer's rule), we need to set up a system of equations based on the given information and then solve for the unknowns, which represent the number of 0.5 litre bottles and 0.7 litre bottles.
Let's denote the number of 0.5 litre bottles as x and the number of 0.7 litre bottles as y.
From the given information, we can set up the following equations:
Equation 1: 0.5x + 0.7y = 16.5 (total volume of moonshine)
Equation 2: 8x + 10y = 246 (total earnings from selling moonshine)
We now have a system of linear equations. To solve it using Cramer's rule, we'll find the determinants of various matrices.
Let's calculate the determinants:
D = determinant of the coefficient matrix
Dx = determinant of the matrix obtained by replacing the x column with the constants
Dy = determinant of the matrix obtained by replacing the y column with the constants
Using Cramer's rule, we can find the values of x and y:
x = Dx / D
y = Dy / D
Now, let's calculate the determinants:
D = (0.5)(10) - (0.7)(8) = -1.6
Dx = (16.5)(10) - (0.7)(246) = 150
Dy = (0.5)(246) - (16.5)(8) = -18
Finally, we can calculate the values of x and y:
x = Dx / D = 150 / (-1.6) = -93.75
y = Dy / D = -18 / (-1.6) = 11.25
However, it doesn't make sense to have negative quantities of bottles. So, we can round the values of x and y to the nearest whole number:
x ≈ -94 (rounded to -94)
y ≈ 11 (rounded to 11)
Therefore, based on the calculation, it appears that Matti had approximately 94 bottles of 0.5 litres and 11 bottles of 0.7 litres in the last patch of moonshine that he sold.
for such more question on litres
https://brainly.com/question/27877215
#SPJ8
Question
Matti is making moonshine in the woods behind his house. He’s selling the moonshine in two different sized bottles: 0.5 litres and 0.7 litres. The price he asks for a 0.5 litre bottle is 8€, for a 0.7 litre bottle 10€. The last patch of moonshine was 16.5 litres, all of which Matti sold. By doing that, he earned 246 euros. How many 0.5 litre bottles and how many 0.7 litre bottles were there? Solve the problem by using the determinant method (a.k.a. Cramer’s rule).
Find the sum of each of the following series:
(a) 2 + 7 + 12 + ...... +92
Answers
where u(n) is the nth term (any term).
u⁰ is out first term (2)
d is the common difference (5)
u(n)=u⁰+nd92 =2 +5n5n =90n =18This sequence admits 19 terms since we start counting from 0 till 18.SummationS= number of terms/2 ×(u¹⁸+u⁰)\(s = \frac{19}{2} \times (92 + 2)\)\(s = 9.5(94)\)
\(s = 893\)
That's ur answer :)
Determine the cubic function that is obtained from the parent function y=x³ after each sequence of transformations.
Vertical compression by a factor of 1/2 , translation down 2 units
Answers
The cubic function obtained from the parent function y=x³ after the given transformations is y = (1/2)(x - 0)³ - 2.
To determine the cubic function obtained from the parent function y=x³ after the given transformations, we need to apply each transformation step by step.
1. Vertical compression by a factor of 1/2: This transformation involves shrinking the graph vertically. In a cubic function, the vertical compression is applied to the coefficient of the leading term. The leading term in the parent function y=x³ is 1x³. By multiplying this term by 1/2, we get (1/2)x³.
2. Translation down 2 units: This transformation involves shifting the graph vertically. In a cubic function, a vertical translation is applied to the constant term. The constant term in the parent function y=x³ is 0. By subtracting 2 from this constant term, we get -2.
Combining these two transformations, we obtain the cubic function: y = (1/2)x³ - 2.
In more detail, the vertical compression by a factor of 1/2 compresses the graph vertically, making it steeper and narrower. The translation down 2 units shifts the entire graph downward by 2 units. By applying these transformations to the parent function y=x³, we obtain the equation y = (1/2)(x - 0)³ - 2.
It's important to note that the sequence of transformations is applied in the order given. If the order were reversed, the resulting function would be different. Transformation operations, such as compression and translation, modify the shape and position of the graph, allowing us to create a variety of functions by modifying the parent function.
Learn more about cubic function here:
brainly.com/question/29337275
#SPJ11
A branch of a certain bank in New York City has six ATMS. Let X represent the number of machines in use at a particular time of day. The cdf of X is as follows: F(X)=⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪0. 6. 10. 39. 67. 92. 971x<00≤x<11≤x<22≤x<33≤x<44≤x<55≤x<66≤xF(X)={0x<0. 060≤x<1. 101≤x<2. 392≤x<3. 673≤x<4. 924≤x<5. 975≤x<616≤x a. Calculate from the cdf values pX(2)
Answers
The probability that exactly 2 ATMs are in use is 0.29, according to the given cdf.
To find the probability that exactly 2 ATMs are in use, we need to subtract the probability that less than 2 ATMs are in use from the probability that less than or equal to 2 ATMs are in use.
From the given cdf, we have:
P(X < 2) = F(2-) = F(1) = 0.1
P(X ≤ 2) = F(2) = 0.39
Therefore, the probability that exactly 2 ATMs are in use is:
P(X = 2) = P(X ≤ 2) - P(X < 2)
= 0.39 - 0.1 = 0.29So,
pX(2) = 0.29.
To learn more about probability Click here:
brainly.com/question/30034780
#SPJ4
What is the coefficient of the x -term of the factorization of 25x²+20 x+4 ?
Answers
The coefficient of the x-term in the factorization of the expression 25x² + 20x + 4 is 20. This is because the x-term is obtained by multiplying the two terms of the factorization that involve x, and in this case, those terms are 5x and 4.
To factorize the expression 25x² + 20x + 4, we need to find two binomial factors that, when multiplied together, yield the original expression. The coefficient of the x-term in the factorization is determined by multiplying the coefficients of the terms involving x in the two factors.
The expression can be factored as (5x + 2)(5x + 2), which can also be written as (5x + 2)². In this factorization, both terms involve x, and their coefficients are 5x and 2. When these two terms are multiplied, we obtain 5x * 2 = 10x.
Therefore, the coefficient of the x-term in the factorization of 25x² + 20x + 4 is 10x, or simply 10.
Learn more about factorization here:
brainly.com/question/14549998
#SPJ11
Ben Amstrong earns $13.57 an hour plus time and a half for weekend work. Last week he worked his regular 40 hours plus 8 hours on Saturday. What was his total pay for the week? A) $542.80 $651.36 B) C) $705.64 $759.92 D)
Answers
Answer:
$651.36
Step-by-step explanation:
13.57x48
A capacitor holds a 8.89 x 10-7 C
charge when 32.0 V are applied to
it. What is its capacitance?

Answers
Answer:2.77*10^-8
Step-by-step explanation:
8.89*10^-7/32.0
The capacitance of the capacitor is approximately 2.78 x 10⁻⁹ Farads (F).
The capacitance of a capacitor can be calculated using the formula:
C = Q / V
Where C represents the capacitance, Q represents the charge stored in the capacitor, and V represents the voltage applied to the capacitor.
In this case, we are given that the charge stored in the capacitor is 8.89 x 10⁻⁷ C and the voltage applied is 32.0 V. Plugging these values into the formula, we get:
C = (8.89 x 10⁻⁷ C) / (32.0 V)
Simplifying the expression, we find:
C ≈ 2.78 x 10⁻⁹ F
The Farad is the SI unit of capacitance, representing the ability of a capacitor to store charge per unit voltage.
To learn more about capacitance click on,
https://brainly.com/question/24346457
#SPJ2
How do you solve this math problem?
5 = 12 + 4
Answers
After a large shipment of lightbulbs goes out, the manufacturer estimates that about 1 % 1% are defective. What is the probability that in a package of 10 lightbulbs 10 lightbulbs, at most 1 lightbulb 1 lightbulb is defective
Answers
The manufacturer estimates that about 1% of the light bulbs are defective. We can solve for the probability of defective bulbs using the binomial probability distribution formula. A package of 10 lightbulbs is taken randomly from the shipment. We have to find the probability that at most 1 lightbulb in a package of 10 lightbulbs is defective.The probability that a single light bulb in the package is defective is 0.01. The probability that in a package of 10 lightbulbs, at most 1 light bulb is defective is 0.9043.
So, the probability that a single light bulb in the package is not defective is (1-0.01) = 0.99.
Probability of at most one defective light bulb in a package of 10 lightbulbs:
P(X ≤ 1) = P(X = 0) + P(X = 1)
= (10C0 × 0.01⁰ × 0.99¹⁰) + (10C1 × 0.01¹ × 0.99⁹)
= (1 × 1 × 0.99¹⁰) + (10 × 0.01 × 0.99⁹)
= 0.9043 (approx.)
The probability that in a package of 10 lightbulbs, at most 1 light bulb is defective is 0.9043 (approx.).
Thus, the probability that in a package of 10 lightbulbs, at most 1 light bulb is defective is 0.9043.
This has been calculated using the binomial probability distribution formula.
To know more about probability visit:
https://brainly.com/question/31828911
#SPJ11
a box with square base and no top is to hold a volume 100. find the dimensions of the box that requires the least material for the five sides. so, the dimensions that minimize the surface area are
Answers
To find the dimensions of the box that requires the least material for the five sides, we need to minimize the surface area while maintaining a volume of 100.
Let's use the following variables:
x = length of one side of the square base
y = height of the box
V = x^2 * y
100 = x^2 * yNow we need to find the surface area of the box with no top:
A = x^2 + 4xy
Our goal is to minimize A. To do this, we'll first express y in terms of x using the volume equation:
y = 100 / x^2Now substitute this expression for y into the surface area equation:
A = x^2 + 4x(100 / x^2)
A = x^2 + (400 / x)
Now we'll find the critical points by taking the derivative of A with respect to x and setting it equal to 0:
dA/dx = 2x - 400 / x^2To find the critical points, set dA/dx = 0:
0 = 2x - 400 / x^2
2x = 400 / x^2
x^3 = 200
Now, solve for x:
x = ∛200 ≈ 5.85Now that we have the value of x, we can find the value of y using our previous expression:
y = 100 / x^2 ≈ 100 / 5.85^2 ≈ 2.93
So, the dimensions that minimize the surface area are approximately:
x = 5.85 units for the base length and width, and y = 2.93 units for the height.
To learn more about “derivative” refer to the https://brainly.com/question/23819325
#SPJ11
What is the area of the trapezoid?

Answers
Answer:
62 square mm.
Step-by-step explanation:
First find the area of the rectangle
4*10=40
Find the area of the Triangle
11*4=44
44÷2=22
Add
40+22=62
Explain how you use a net to find the surface area of a prism.
Answers
Answer:
lay the net out with numbers then add all of them
Step-by-step explanation:
Our physics club has $20$ members, among which we have 3 officers: President, Vice President, and Treasurer. However, one member, Alex, hates another member, Bob. How many ways can we fill the offices if Alex refuses to serve as an officer if Bob is also an officer
Answers
We can fill the offices in 7146 ways if Alex refuses to serve as an officer if Bob is also an officer.
Given that we have 20 members in a physics club, and among which 3 are officers: President, Vice President, and Treasurer. One of the members, Alex refuses to serve as an officer if Bob is also an officer. The problem is to find out how many ways we can fill the offices under these circumstances.
Let's say we start by filling the post of President. This post can be filled in 20 ways.
After we have filled the President's post, we move on to the Vice-President's post. This post can be filled in 19 ways, as there are only 19 people left to choose from. Finally, we fill the Treasurer's post, which can be done in 18 ways. Thus the total number of ways we can fill the offices is equal to:$$20 \times 19 \times 18 = 6840$$Therefore, we can fill the offices in 6840 ways if Alex refuses to serve as an officer if Bob is also an officer.
In the given question, we have been given that we have 20 members in a physics club. Out of the 20 members, 3 of them are officers. We are also given that Alex does not want to serve as an officer if Bob is also an officer. We are required to find out the number of ways we can fill the offices under these circumstances.So let's say we start by filling the post of President.
There are 20 members in the club, and hence 20 ways in which we can select the President. After we have filled the post of the President, we move on to the Vice-President's post. But here we have to keep in mind that Alex does not want to serve as an officer if Bob is also an officer. So, let's consider two cases:
Bob is not selected as the PresidentIn this case, Bob is available for selection as the Vice President. Therefore, we can select the Vice President in 19 ways. After this, we can select the Treasurer in 18 ways.
Hence the total number of ways in which we can select the officers when Bob is not selected as the President is equal to:$$20 \times 19 \times 18 = 6840$$.
Bob is selected as the President.In this case, Bob is not available for selection as the Vice President. Therefore, we can select the Vice President in 18 ways (as we can't select Bob). After this, we can select the Treasurer in 17 ways (as we can't select Bob and the Vice President). Hence the total number of ways in which we can select the officers when Bob is selected as the President is equal to:$$1 \times 18 \times 17 = 306$$.
Therefore, the total number of ways in which we can fill the offices when Alex refuses to serve as an officer if Bob is also an officer is equal to the sum of the two cases:$$6840 + 306 = 7146$$Thus, we can fill the offices in 7146 ways if Alex refuses to serve as an officer if Bob is also an officer.
We can fill the offices in 7146 ways if Alex refuses to serve as an officer if Bob is also an officer.
To know more about total number of ways visit:
brainly.com/question/31429428
#SPJ11
help me pls and thank you :)
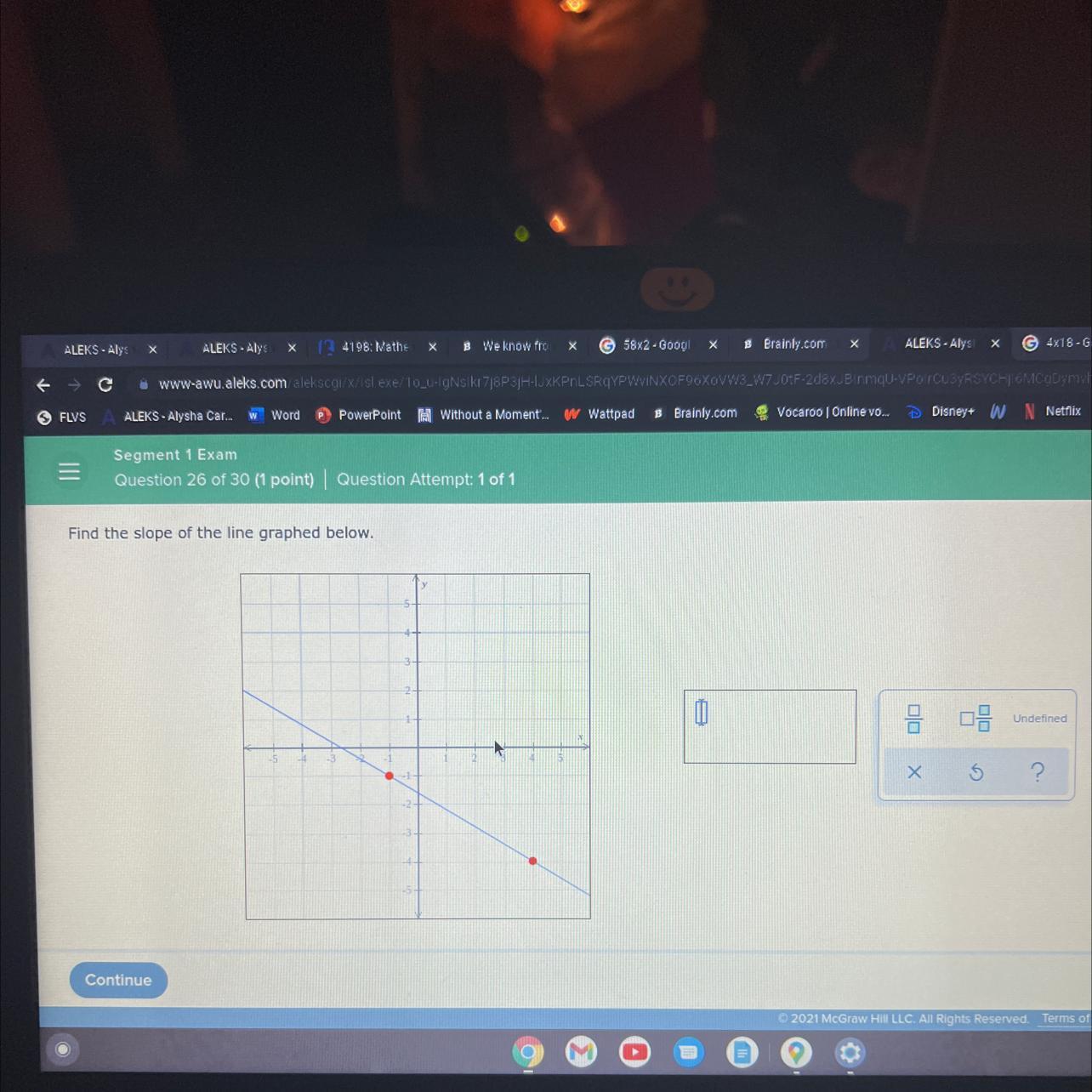
Answers
Answer:
\( \frac { - 3}{5} \)
What is the expanded form of 6.02?

Answers
6x2+2x0.01
The Decimal point is a fraction whose denominator is a power of ten and whose numerator is expressed by figures placed to the right of the decimal point.
Given information:
Expanded Form of 6.02
\(6.02 = (6 \times 100) + (2 \times \frac{1}{102} )\\6.02 = (6 \times 1) + (2 \times \frac{1}{100} )\\6.02 = 6 + \frac{2}{100}\\ 6.02 = 6 + 0.02\)
For more information refer to the link given below:
https://brainly.com/question/104324
Name a point that is collinear with points E and H
Answers
Answer:
Point J
Step-by-step explanation:
The image of the points are missing and so i have attached it.
Collinear points are simply points that are on the same line.
From the attached image, we see that points E and H are on the same line of the cube.
Now, the other point that lies on that same line as seen in the image is point J.
Thus, point J is collinear to points E & H.
