what is two plus two
Answers
Related Questions
If you want to prove you have correctly found the solution to a linear system, why do you have to substitute the solution into both equations?
Answers
Answer:
See below for explanation.
Step-by-step explanation:
As we know, if we substitute a solution in an equation, there can be two circumstances:
True - If both sides of equation are equal or same after substituting the solution in an equation, that equation is true and that means a point or solution lies on the graph.False - If both sides of equation are not equivalent or different after substituting the solution in an equation, that equation is false and that means a point or solution does not lie on graph.What does substituting the solution tell you? It tells you whether if that solution you have solved or got is correct or not. Graph wise, a point is a part of an equation if LHS = RHS but a point lies differently or separates from graph if LHS ≠ RHS.
KEYWORD
LHS - Left-Handed Side - It is always used to refer as left side of equation.RHS - Right-Handed Side - It is always used to refer as right side of equation.Do you know? A single equation such as x + 5 = 2 can be written in simultaneous equations by letting both LHS and RHS = y as we obtain y = x + 5 for first equation and y = 2 as second equation.
Next, let’s talk about simultaneous equations or system of equations. They are technically the same as one-variable equation except you learn how to convert from one-variable equations to two-variable simultaneous equations and some substitutions method as well as learn some tricks to solve for simultaneous equations. The solution in two-variable simultaneous equations is in (x,y) term so you have both x and y solution. Instead of substituting one x-value solution, unlike simultaneous equations, you need to substitute both x and y.
I said that substituting the solution(s) in mathematics are to check whether if that point or solution does lie on a graph. If a point lies on a graph or equation, that solution is valid and correct - if not, the solution is incorrect.
We have cleared out the reason why we have to substitute the solution(s) in to check. Now, why do we have to substitute in both equations rather only one? The answer is to make sure in 100%. Sometimes, when substituting the (x,y) solution in simultaneous equations, one of two equations may not have same LHS and RHS respectively.
For example, when substituting x = 2 and y = 4 in first equation, we get 2 = 2 but when we substitute in the second equation, we get 4 = 2. See that the first equation is true when substituting the solution in because both sides are equal but the second equation is false because both sides are not equal. That means (2,4) is not solution to the simultaneous equations as the second equation is false. For a solution to exist in simultaneous equations, a point (x,y) must satisfy both equations which means both equations have to be true when substituting a solution (x,y).
To summarize what I said all above:-
Substituting solutions in the simultaneous equations is to check whether if the solutions are correct or apart of graphs/equations.If a one-variable equation is true i.e 3 = 3 as example when substituting a solution in then the solution is correct. Otherwise, it’s not correct.If a two-variable equations are true for both LHS and RHS i.e both equations must have same LHS and RHS respectively then the solutions are correct. Otherwise, it’s not, even if one equation has same LHS and RHS but if the second equation does not have same LHS and RHS then the solutions are false.If you still have questions or queries about this problem or my answer, you can let me know in the comment!
What is the horizontal asymptote of the function f (x)= x^2-25/2x^2 ?
Answers
Find all real solutions for the equation -21n + n² = -98. Separate multiple
solutions with commas if necessary.
Answers
Answer:
n=7, 14
Step-by-step explanation:
-21n + n² = -98
n² - 21n = -98
n² - 21n + 98 = -98 + 98
n² - 21n + 98 = 0
n² - 7n - 14n + 98 = 0
n(n-7) - 14(n-7) = 0
(n-14)(n-7) = 0
n-14=0 ==> n=14
n-7=0 ==> n=7
n=7, 14
A Two-Way ANOVA experiment has: • Factor A with 3 levels • Factor B with 7 levels • 100 Replications If we fit the Interaction model, how many degrees of freedom for Error are there? o 92 o 2090 o 69 o 80 o 2092 o 2079 o 2080 o 90 o 2069
Answers
The degrees of freedom for Error is 80.
Two-Way ANOVA DegreesTo calculate the degrees of freedom for error in a Two-Way ANOVA with an interaction model, we need to use the following formula:df(Error) = (n-1) - df(A) - df(B) - df(AB)
where:n is the total number of observations (replications)
df(A) is the degrees of freedom for factor A (number of levels - 1)
df(B) is the degrees of freedom for factor B (number of levels - 1)
df(AB) is the degrees of freedom for the interaction between A and B (df(A) x df(B))
In this case, we have:n = 100
df(A) = 3 - 1 = 2
df(B) = 7 - 1 = 6
df(AB) = 2 x 6 = 12
Plugging these values into the formula, we get:df(Error) = (100-1) - 2 - 6 - 12
df(Error) = 79
Therefore, the answer is 80 (closest option).
Learn more about Two-Way ANOVA Degrees here:
https://brainly.com/question/23638404
#SPJ1
Question 2 (10 points)
Classify <1 and < 2 using all names that apply.
a Vertical
b Adjacent
C Complementary
d Supplementary

Answers
Answer:
B. adjacent and D. supplementary
A quadratic function may have one root, two roots, or no______ roots.
Answers
Answer:
Step-by-step explanation:
A test of : versus : is performed using a significance level of =0.05. The value of the test statistic is z= -2.14. If the true value of μ is 58, does the conclusion result in a Type I error, a Type II error, or a correct decision?
Answers
The conclusion results in a Type I error.
How does the conclusion lead to a Type I error?To determine whether the conclusion results in a Type I error, a Type II error, or a correct decision, we need to analyze the given information.
In this scenario, the test is conducted to compare a hypothesized population mean, denoted as μ, with a specific value of 58. The null hypothesis (H₀) states that μ is equal to 58, while the alternative hypothesis (H₁) suggests that μ is not equal to 58.
A significance level, denoted as α, is set at 0.05, which means that the researcher is willing to accept a 5% chance of making a Type I error - rejecting the null hypothesis when it is actually true.
The test statistic, z, is calculated to assess the likelihood of the observed data given the null hypothesis. In this case, the test statistic value is z = -2.14.
Since the test statistic is negative and falls in the rejection region of a two-tailed test, we can compare its absolute value to the critical value for a significance level of 0.05.
Looking up the critical value in the standard normal distribution table, we find that for a two-tailed test with α = 0.05, the critical value is approximately 1.96.
Since |z| = |-2.14| = 2.14 > 1.96, we have sufficient evidence to reject the null hypothesis.
Now, if the true value of μ is actually 58, and we reject the null hypothesis that μ = 58, it means we have made a Type I error - concluding that there is a difference when, in reality, there is no significant difference.
Therefore, the conclusion in this case results in a Type I error.
Learn more about Type I error
brainly.com/question/32609769
#SPJ11
factoring trinomials with leading coefficient greater than 1. Learn how to factor quadratic expressions as the product of two linear binomials. For example, 2x²+7x+3=(2x+1)(x+3).
Answers
The factored quadratic expression of 2x²+7x+3 as the the product of two linear binomials is (2x+1)(x+3)
To factor trinomials with a leading coefficient greater than 1, follow these steps
Multiply the coefficient of the leading term by the constant term.
Find two factors of the product from step 1 that add up to the coefficient of the middle term.
Rewrite the middle term using the two factors found in step 2.
Factor by grouping the first two terms and the last two terms.
Factor out the common factor.
Let's use the example 2x²+7x+3 to demonstrate these steps
2 x 3 = 6
Find two factors of 6 that add up to 7: 6 and 1
Rewrite the middle term as 6x + 1x
Factor by grouping
2x² + 6x + 1x + 3
2x(x + 3) + 1(x + 3)
Factor out the common factor
(2x + 1)(x + 3)
Therefore, 2x²+7x+3 can be factored as (2x + 1)(x + 3).
Learn mnore about Trinomial here
brainly.com/question/9702142
#SPJ4
In VWX, v = 390 inches, w = 390 inches and x=500 inches. Find the measure of ZX
to the nearest 10th of a degree.
Answers
Answer:
79.737≈79.7
Step-by-step explanation:
x < 2 is the solution to which of the following compound inequalities?

Answers
Answer:
see below
Step-by-step explanation:
It works well to think about what these compound inequalities mean. One way to do that is to graph them, or to imagine what the graph of them looks like.
Since the result is a single inequality (x < 2), the compound will be "and" with x < 2 being more restrictive, or will be "or" with x < 2 being the least restrictive of completely overlapping inequalities.
Of the choices offered, C is the one of interest.
_____
Comment on other choices
A has all real numbers as solutions except in the range 2 ≤ x ≤ 3.
B has no solutions
C simplifies to x < 2 . . . . the one we want
D simplifies to x < 4

2
Carter is going on a 16.5
mile hike through the
Grand Canyon. If he wants
to spread out his hike
evenly over the next 6
hours, how many miles
should he hike per hour?
NIC
Answers
Answer:
2.75 miles per hour
Step-by-step explanation:
16.5/6
A large university provides housing for 15 percent of its graduate students to live on campus. The university’s housing office thinks that the percentage of graduate students looking for housing on campus may be more than 15 percent. The housing office decided to survey a random sample of graduate students, and 78 of the 433 respondents say that they are looking for housing on campus. a) On the basis of the survey data, would you recommend that the housing office consider increasing the amount of housing on campus available to graduate students? Give appropriate evidence to support your recommendation. [Conduct a hypothesis test: State,Plan, Do,Conclude] b) Interpret the p-value obtained in part a) in context. c) In addition to the 433 graduate students who responded to the survey, there were 21 who did not respond. If these 21 had responded, is it possible that your recommendation would have changed? Explain. d) Describe what a Type II error would be in the context of the study, and also describe a consequence of making this type of error. e) Describe what a Type I error would be in the context of the study, and also describe a consequence of making this type of error.
Answers
a) Hypothesis test:
Null hypothesis (H0): The percentage of graduate students looking for housing on campus is equal to 15%.
Alternative hypothesis (Ha): The percentage of graduate students looking for housing on campus is greater than 15%.
To test the hypothesis, we can use a one-sample proportion test. We will calculate the test statistic and compare it to the critical value or p-value to make a decision.
The observed proportion of graduate students looking for housing on campus is 78/433 = 0.1804.
Using a significance level (α) of 0.05, we will conduct the test and calculate the test statistic and p-value.
Plan:
Test statistic: z = (p - p) / sqrt(p(1-p)/n)
where p is the observed proportion, p is the hypothesized proportion (0.15), and n is the sample size (433).
Do:
Calculating the test statistic:
z = (0.1804 - 0.15) / sqrt(0.15 * 0.85 / 433)
z ≈ 2.07
Conclude:
Since the test statistic is 2.07, we compare it to the critical value or calculate the p-value.
The critical value for a one-sided test with a significance level of 0.05 is approximately 1.645. Since 2.07 > 1.645, the test statistic falls in the rejection region.
The p-value associated with the test statistic of 2.07 is less than 0.05. Therefore, we reject the null hypothesis.
Based on the survey data, there is evidence to suggest that the percentage of graduate students looking for housing on campus is greater than 15%. The housing office should consider increasing the amount of housing available to graduate students.
b) The p-value obtained in part a) represents the probability of obtaining a test statistic as extreme as the one observed (or more extreme), assuming the null hypothesis is true.
In this case, the p-value is less than 0.05, which suggests strong evidence against the null hypothesis. It indicates that the observed proportion of graduate students looking for housing on campus is significantly higher than the hypothesized proportion of 15%.
c) Including the 21 non-respondents would change the sample size and potentially affect the estimated proportion. If these additional respondents had similar characteristics to the 433 who responded, it is possible that the recommendation might still remain the same.
However, the exact impact depends on the responses of the non-respondents, so it is difficult to determine the precise effect without their data.
d) Type II error in this study would occur if the housing office fails to increase the amount of housing on campus when it is actually necessary (i.e., the percentage of graduate students looking for housing on campus is higher than 15%).
This means the null hypothesis would not be rejected when it should have been. A consequence of this type of error would be the unmet demand for housing, potentially causing dissatisfaction among graduate students and a shortage of available housing options.
e) Type I error in this study would occur if the housing office increases the amount of housing on campus when it is not necessary (i.e., the percentage of graduate students looking for housing on campus is not higher than 15%). This means the null hypothesis would be rejected incorrectly.
A consequence of this type of error would be allocating resources and efforts towards increasing housing capacity unnecessarily, which could result in wastage of resources and potentially impact other areas of the university's operations.
Visit here to learn more about Null hypothesis brainly.com/question/30821298
#SPJ11
i only need number 10 plz help!!!!!!!

Answers
9514 1404 393
Answer:
DE ≈ 9.49, EF ≈ 8.06, FD ≈ 14.87obtuse scalene triangleStep-by-step explanation:
For finding side lengths, it is convenient to work with the differences of the coordinates.
DE = E(-1, -3) -D(8, -6) = (-9, 3)
EF = F(-2, 5) -E(-1, -3) = (-1, 8)
FD = D(8, -6) -F(-2, 5) = (10, -11)
Then the lengths are ...
DE = √((-9)² +3²) = √90 = 3√10 ≈ 9.49
EF = √((-1)² +8²) = √65 ≈ 8.06
FD = √(10² +(-11)²) = √221 ≈ 14.87
The lengths are all different and the largest angle is obviously more than 90°, so the triangle is an obtuse scalene triangle.

what is the value of log64 8 ?
Answers
Answer:
0.5-----------------
Find the value of log₆₄ 8:
\(log_{64} \ 8 = log_{64}\ (64)^{1/2}=\cfrac{1}{2}\ log_{64}\ 64 = 0.5\)phyllis teaches marketing at a local college. she wants to select one freshman and one sophomore to attend a conference. if she teaches 12 freshman and 14 sophomores, how many combinations of students could be selected?
Answers
By using the concept of Permutation and Combination, Counting Principle Phyllis can make 168 ways to select students.
Permutation and Combination are about making arrangements and making selections on the basis of certain formulas
The re-arranging of any given sorted/ordered set is called a permutation. The “permutation” word actually tells us that change the linear order of the ordered set.
Selecting items from a large collection without taking any care about their order is called combinations.
We need to select one freshman out of 12 freshmen. So selecting r things from n things we can do selection in nr ways, so we can do a selection of freshmen in 12c1 ways
Similarly, we need to select one sophomore out of 14 sophomores, so we can do a selection of sophomores in 14c1 ways
We know that ncr is equivalent to \(\frac{n!}{r!(n-r)!}\)
So, using this concept total number of ways to select a student
= ((12c1)×(14c1))
=12×14
=168 ways
Hence Phyllis can select students in 168 ways
To know more about Counting Principle, Permutations and Combinations visit here:
https://brainly.com/question/28720645
#SPJ4
15 cm
T
9.9 cm
12 cm
-
Find volume

Answers
Step-by-step explanation:
The volume = 15 × 4.2 × 9.9 = 623.7
please give me a brainliest answer
X+4y=8 identify the x intercept
Answers
Answer: (8, 0)
Step-by-step explanation:
X intercept is when y = 0
\(x+4*0=8\\x=8\)
unlike most packaged food products, alcohol beverage container labels are not required to show calorie or nutrient content. an article reported on a pilot study in which each of 56 individuals in a sample was asked to estimate the calorie content of a 12 oz can of beer known to contain 153 calories. the resulting sample mean estimated calorie level was 191 and the sample standard deviation was 86. does this data suggest that the true average estimated calorie content in the population sampled exceeds the actual content? test the appropriate hypotheses at significance level 0.001.state the appropriate null and alternative hypotheses.
Answers
Using a t-distribution table with 55 degrees of freedom (n-1), we find the critical t-value for a one-tailed test at a significance level of 0.001 is 3.600. Since our calculated t-value (4.78) is greater than the critical t-value (3.600), we can reject the null hypothesis and conclude that the true average estimated calorie content in the population is likely greater than the actual content.
To test this hypothesis, we need to state the appropriate null and alternative hypotheses. The null hypothesis (H0) would be that the true average estimated calorie content in the population is equal to the actual content, while the alternative hypothesis (Ha) would be that the true average estimated calorie content in the population is greater than the actual content.
1. State the null and alternative hypotheses:
- Null hypothesis (H0): The true average estimated calorie content is equal to the actual content (μ = 153).
- Alternative hypothesis (H1): The true average estimated calorie content exceeds the actual content (μ > 153).
2. Choose a significance level (α): In this case, α = 0.001.
3. Calculate the test statistic:
- Sample mean (X) = 191
- Sample standard deviation (s) = 86
- Sample size (n) = 56
The test statistic for a one-sample t-test is given by the formula:
t = (X - μ) / (s / √n)
Plugging in the values: t = (191 - 153) / (86 / √56) ≈ 3.55
4. Determine the critical value and rejection region: Since this is a one-tailed test with α = 0.001 and 55 degrees of freedom (n - 1 = 56 - 1 = 55), we find the critical value from a t-distribution table to be approximately 3.148.
5. Compare the test statistic to the critical value: In this case, t = 3.55 > 3.148.
6. Make a decision: Since our test statistic is greater than the critical value, we reject the null hypothesis. This suggests that the true average estimated calorie content in the population sampled exceeds the actual content at a significance level of 0.001.
In conclusion, based on the data from the article and the pilot study sample, there is evidence to suggest that the true average estimated calorie content in the population sampled exceeds the actual content of a 12 oz can of beer known to contain 153 calories at a significance level of 0.001.
Learn more about Hypothesis:
brainly.com/question/31319397
#SPJ11
find the final amount when $700 investment at a compound interest of 5% semi annually for 4 years
Answers
The final amount of the investment is $852.88
Finding the final amount of the investmentThe formula for the compound interest is given by:
A = P(1 + r/n)^(nt)
Where:
A = final amountP = principal amount (initial investment)r = annual interest rate (as a decimal)n = number of times the interest is compounded per yeart = time (in years)In this case, P = $700, r = 5% = 0.05, n = 2 (semi-annually compounded), and t = 4 years.
Plugging in the values, we get:
A = 700(1 + 0.05/2)^(2*4)
= 700(1.025)^8
= $852.88 (rounded to two decimal places)
Therefore, the final amount after 4 years is $852.88
Read more about compound interest at
https://brainly.com/question/24924853
#SPJ1
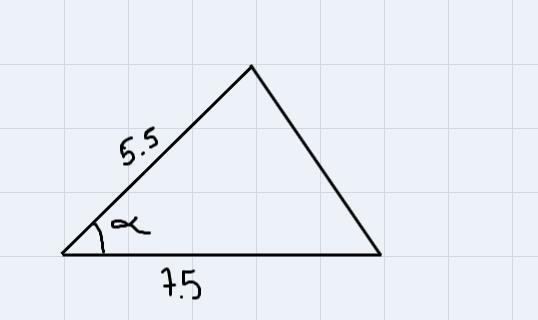
The area of a triangle is 15. Two of the side lengths are 5.5 and 7.5 and the includedangle is acute. Find the measure of the included angle, to the nearest tenth of adegree.
Answers
α =46º
1) Let's start by gathering the data:
S = 15 u²
a= 5.5
b= 7.5
Sketcing out:
2) One of the formulas to find out the area of a triangle is:
\(S=\frac{ab\cdot\sin (\alpha)}{2}\)Plugging the given data into the formula we have:
\(\begin{gathered} 15=\frac{5.5\cdot7.5\sin (\alpha)}{2}\text{ }\times2 \\ 30\text{ =41.25}\cdot\sin (\alpha) \\ \frac{30}{41.25}=\frac{\text{41.25}\cdot\sin (\alpha)}{41.25} \\ 0.72=\sin (\alpha) \end{gathered}\)2.2) Since we want to know the measure of that angle, then let's make use of the arcsine of (0.72)
\(\begin{gathered} \alpha=\sin ^{-1}(0.72) \\ \alpha=46.05\approx46 \end{gathered}\)3) Hence, the missing acute angle is α =46º (rounded off to nearest whole number)
Competency: Write the linear equations Ax + By = C. Give the value of A,B, and C,.

Answers
Answer:
see explanation
Step-by-step explanation:
(1)
y = - x + 4 ( add x to both sides )
x + y = 4
with A = 1, B = 1, C = 4
(2)
y = 5x + 7 ( subtract y from both sides )
0 = 5x - y + 7 ( subtract 7 from both sides )
- 7 = 5x - y , that is
5x - y = - 7
with A = 5, B = - 1, C = - 7
----------------------------------------------------------
(1)
2x + y = 9 ( subtract 2x from both sides )
y = - 2x + 9
with m = - 2, c = 9
(2)
5x + 2y = 7 ( subtract 5x from both sides )
2y = - 5x + 7 ( divide terms by 2 )
y = - \(\frac{5}{2}\) x + \(\frac{7}{2}\)
with m = - \(\frac{5}{2}\) , c = \(\frac{7}{2}\)
help algebra 2 please

Answers
Answer:
option 4
Step-by-step explanation:
g(x) = x² + 4x + 4
= x² + 2 * x * 2 + 2² {Compare with identity a²+ 2ab +b² = (a +b)²}
= (x + 2)²
\((\dfrac{f}{g})(x) = \dfrac{(x +2)}{(x+2)*(x+2)}\\\\\\= \dfrac{1}{x+2}\)
The angles of elevation to an airplane from two points A and B on level ground are 58° and 76°, respectively. The points A and B are 2.1 miles apart, and the airplane is east of both points in the same vertical plane. Find the altitude of the plane. (Round your answer to two decimal places.)
Answers
Answer:
90
Step-by-step explanation:
45x2=90
In ΔNOP, o = 92 cm, p = 23 cm and ∠N=138°. Find the area of ΔNOP, to the nearest square centimeter.
Answers
The area of triangle NOP is given as follows:
1416 cm².
How to obtain the area of the triangle?The area of a triangle, given two side lengths and the angle between them, is given by the multiplication of the side lengths and the sine of the angle between them.
The parameters for this problem are given as follows:
Side lengths of 92 cm and 23 cm.Angle between them of 138º.Hence the area of the triangle is given as follows:
A = 92 x 23 x sine of 138 degrees
A = 1416 cm².
More can be learned about the area of a triangle at https://brainly.com/question/21735282
#SPJ1
Systolic Blood Pressure (SBP) of 13 workers follows normal distribution with standard deviation 10. SBP are as follows: 129, 134, 142, 114, 120, 116, 133, 142, 138, 148 , 129, 133, 140_ Find the 99%0 confidence interval for the mean SBP level: (124.84 (129.84 (126.84 (125.84 139.16) 139.16) 137.16) 138.16)
Answers
Answer:The 99% confidence interval is
To find the 99% confidence interval for the mean systolic blood pressure (SBP) level, we use the formula:
CONFIDENCE INTERVAL = Mean ± Z * (Standard Deviation / √n)
Where:
Mean is the sample mean of SBP
Z is the Z-score corresponding to the desired confidence level
Standard Deviation is the population standard deviation
Explanation:
Given that the sample size is 13 and the standard deviation is 10, we need to calculate the sample mean and the Z-score for the 99% confidence level.
First, we calculate the sample mean:
Mean = (129 + 134 + 142 + 114 + 120 + 116 + 133 + 142 + 138 + 148 + 129 + 133 + 140) / 13
= 1724 / 13
≈ 132.62
Next, we need to determine the Z-score for a 99% confidence level. The Z-score can be found using a Z-table or a statistical calculator. For a 99% confidence level, the Z-score is approximately 2.576.
Now, we can calculate the confidence interval:
Confidence Interval = 132.62 ± 2.576 * (10 / √13)
132.62 ± 2.576 * (10 / 3.6056)
≈ 132.62 ± 2.576 * 2.771
≈ 132.62 ± 7.147
Therefore, the 99% confidence interval for the mean SBP level is approximately (125.47, 139.77).
Which of the following expressions is equivalent to (y − 3)4?
A) y4 − 12y3 + 54y2 − 108y + 81
B) y4 + 12y3 + 54y2 + 108y + 81
C) y4 − 27y3 + 9y2 − 3
D) y3 − 9y2 + 27y − 27
Answers
The binomial expansion of (y - 3)⁴ is B) y⁴ - 12y³ + 54y² - 108y + 81.
What is the binomial theorem?The Binomial Theorem is the method of expanding an expression that has been raised to any finite power.
An expression of two terms having a degree n can be represented as,
(a - b)ⁿ = \(^nC_na^n - ^nC_{n-1}a^{n-1}b+^{n}C_{n-2}a^{n-2}b^2+...(-1)^n\times^nC_0a^0b^n\).
Given, (y - 3)⁴ = \(^4C_4y^4.3^0 - ^4C_3y^3.3 + ^4C_2y^23^2-^4C_1y.3^3+^4C_0y^03^4\).
(y - 3)⁴ = y⁴ - 12y³ + 54y² - 108y + 81.
learn more about binomial theorem here :
https://brainly.com/question/27813780
#SPJ1
Find the x- and y- intercepts of the linear equation y=x+5 x-intercept=? y-intercept=?
Answers
In x axis y =0
-x=5
X=-5
In y axis x=0
Y=5
a drawer has ten blue, ten white, and ten red socks. without looking at them you pull some socks out. what is the least number of socks you need to pull to ensure you get two pairs of matching socks? justify your answer.
Answers
Answer:
The answer is 7 socks.
Step-by-step explanation:
To ensure one matching pair, you need to pull out 4 socks. If none of the first three match, the fourth one will guarantee a matching pair.
You will then need to pull out 3 more socks, for a total of 7 socks, to ensure two matching pairs.
Select the correct answer. Consider functions h and k. The picture shows a one-to-one function diagram. x has values of minus 2, minus 1, 0, 1, and 2, and k of x has values of minus 2, minus 5, minus 6, minus 5, and minus 2. Every x value has a relationship in k of x. What is the value of ? A. B. C. D.
Answers
The numeric value of the composite function at x = 1 is given as follows:
(h ∘ k)(1) = 28.
What is the composite function of f(x) and g(x)?The composite function of f(x) and g(x) is given by the rule presented as follows:
(f ∘ g)(x) = f(g(x)).
For the composition of two functions, we have that the output of the inner function, in this example g(x), serves as the input of the outer function, in this case f(x).
Hence the numeric value at x = 1 for the function in this problem is:
h(k(1)).
The numeric value of k at x = 1 is:
k(1) = 3.
Then, as the numeric value of h at x = 3 is of 28, the composite function is:
(h ∘ k)(1) = 28.
Missing InformationThe problem is given by the image presented at the end of the answer.
More can be learned about composite functions at https://brainly.com/question/10687170
#SPJ1

The average satisfaction rating for all hospitals were 7.8 (on a 1-10 scale) with a sigma of .5. The average satisfaction for Riverside community hospital was 8.1 with a standard deviation of 1.5. What test should be used
Answers
A one-sample t-test is the appropriate test to compare the average satisfaction rating of Riverside community hospital to the population average.
To determine what test should be used in this scenario, we need to consider the nature of the data and the objective of the analysis.
Based on the given information, we have two sets of data: the average satisfaction rating for all hospitals (population) and the average satisfaction rating for Riverside community hospital (sample).
If our objective is to compare the average satisfaction rating of Riverside community hospital to the population average, we can use a hypothesis test. Specifically, we can perform a one-sample t-test.
The one-sample t-test allows us to compare a sample mean to a known population mean when the population standard deviation is unknown. In this case, we know the population mean (7.8) and the population standard deviation (0.5), which makes the one-sample t-test appropriate.
By comparing the average satisfaction rating of Riverside community hospital (8.1) to the population mean (7.8), along with the sample standard deviation (1.5) and the known population standard deviation (0.5), we can conduct a one-sample t-test to determine if the difference is statistically significant.
Therefore, a one-sample t-test is the appropriate test to compare the average satisfaction rating of Riverside community hospital to the population average.
for such more question on sample t-test
https://brainly.com/question/20166137
#SPJ8