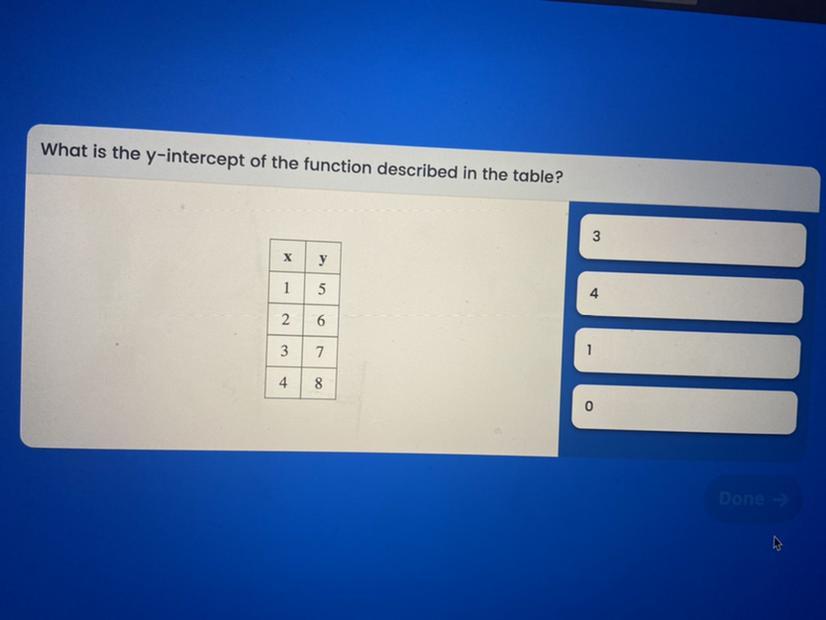
Answers
Answer: 4
Step-by-step explanation:
Related Questions
marco bought 5 movies for $53.10 Vance bought 3 movies for $31.71 who got the better deal
Answers
Answer:
vance got the better deal
Step-by-step explanation:
Help me please I am having trouble figuring out the answer. Help me find the ratio.

Answers
Answer:
not equivalent to meteorologists ratio
Step-by-step explanation:
meteorologists ratio is
rainy days : sunny days = 2 : 5
last months weather is
rainy days : sunny days
= 10 : 20 ( divide both parts by LCM of 10 )
= 1 : 2 ← not equivalent to 2 : 5
Find the sum or difference of the polynomials (x2−xy+y2) − (x2+xy+y2)
Answers
Find the sum of the following series.
PLEASE SOMEONE HELP!!!

Answers
The given sum for n = 1 to n = 15 is equal to 255, so the correct option is B.
How to find the sum of the given series?
We want to find the sum of the series whose elements are of the form:
(2n + 1)
From n = 1 to n = 15.
Then our sum will be:
(2*1 + 1) + (2*2 + 1) + ... + (2*15 + 1).
3 + 5 + ... + 31
This is the sum of all odd numbers in the interval [3, 31]
Which gives:
\(S = 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 + 25 + 27 + 29 + 31 = 255\)
So the correct option is B.
If you want to learn more about sums:
https://brainly.com/question/24295771
#SPJ1
Question 1 [15 points] Consider the following complex number c. The angles in polar form are in degrees: c = a +ib = 2; 3³0 + 3e¹454e145 Determine the real part a and imaginary part b of the complex number without using a calculator. (Students should clearly show their solutions step by step, otherwise no credits). Note: cos(90) = cos(-90) = sin(0) = 0; sin(90) = cos(0) = 1; sin(-90) = -1; sin(45) = cos(45) = 0.707
Answers
The real part (a) of the complex number is 2, and the imaginary part (b) is 3.
To determine the real and imaginary parts of the complex number without using a calculator, we can analyze the given polar form of the complex number c = 2; 3³0 + 3e¹454e145.
In polar form, a complex number is represented as r; θ, where r is the magnitude and θ is the angle. Here, the magnitude is 2, and we need to determine the real (a) and imaginary (b) parts.
The real part (a) corresponds to the horizontal component of the complex number, which can be found using the formula a = r * cos(θ). In this case, a = 2 * cos(30°) = 2 * 0.866 = 1.732.
The imaginary part (b) corresponds to the vertical component, which can be found using the formula b = r * sin(θ). In this case, b = 2 * sin(30°) = 2 * 0.5 = 1.
Therefore, the real part (a) of the complex number is 2, and the imaginary part (b) is 3.
Learn more about Complex number
brainly.com/question/20566728
#SPJ11
____% of 80 = 68
Also could you explain the steps too?
Answers
What % of 80 is 68?
P% of 80 is 68
Equation: P% * X = Y
Solving our equation for P
P% = Y/X
P% = 68/80
p = 0.85
Convert decimal to percent:
P% = 0.85 * 100 = 85%
If point B is reflected across the y axis, what are the coordinates of the new point?
(-3,2)
(-2,-3)
(-2,3)
(3,-2)

Answers
Answer: (3,-2)
Step-by-step explanation: We're reflecting to the y-axis, thus, we're going to reflect to the right.
(-x,-y) ⇒ (x,-y)
Our current coordinate is (-3,-2)...let's convert it now...
(3,-2)
I hope this helps!
Answer:
(3, -2).
Step-by-step explanation:
When you reflect across the y axis the y coordinate stays the same and the x axis changes sign : (x, y) --> (-x, y).
So B (-3, -2) --> (3, -2).
The number of bottles a machine fills is proportional to the number of minutes the machine operates. The machine fills 250 bottles every 20 minutes. Create a graph that shows the number of bottles, y, the machine fills in x minutes.
How do i do this if the minutes only go up to 9 and the y axis is only 125???
Answers
Answer:
Since the machine fills 250 bottles every 20 minutes, we can write the proportion:
250 bottles / 20 minutes = y bottles / x minutes
Simplifying this proportion, we get:
y = (x/20) * 250
This equation represents a linear relationship between the number of bottles (y) and the number of minutes (x), where the slope is 250/20 = 12.5 bottles per minute.
To create a graph, you can plot the points (0, 0) and (9, 112.5) since the y-axis only goes up to 125. This will give you a straight line that starts at the origin and goes up to about 112.5 on the y-axis at x = 9.
Step-by-step explanation:
All digits in a dropdown number are different and one of its digits is the average of all its digits. It has at least two digits. For example, 5021 is a dropdown number, but neither 4389 nor 6033 is a dropdown number. a Find the smallest dropdown number.
Answers
The dropdown numbers is an illustration of combination
The smallest dropdown number is 1025
How to determine the smallest dropdown number?From the question, we have the following parameters:
The dropdown number is 4-digitThe digits are different.We start counting from 1023, 1024, 1025, 1026...........
The sum of digits in 1023 is 6, and the average is 1.5The sum of digits in 1024 is 7, and the average is 1.75The sum of digits in 1025 is 8, and the average is 2The number 1025 satisfies the given conditions
Hence, the smallest dropdown number is 1025
Read more about combination at:
https://brainly.com/question/11732255
Which property is demonstrated?
8.1.6 = 6.1.8
A.) associative property of addition
B.)commutative property of multiplication
C.) associative property of multiplication
D.) commutative property of addition
Answers
Answer:
community property addition
How many positive four-digit integers have the three digits the same and a different fourth digit (in some order)
Answers
Answer:
81 * 4 = 324.
Step-by-step explanation:
There are 81 * 4 = 324 such integers.
There are 9000 four-digit integers from 1000 to 9999. Let’s refer to the digit that occurs three times as the triplet and the digit that occurs once as the singleton.
In the first (most significant) position there are 9 possible values for the singleton, 1 through 9. In each case there are also 9 possible values for the triplet. For example if the singleton was a 1, the triplets could be anything but a 1: 1000, 1222, 1333, …, 1999. So there are 9 * 9 = 81 cases with the singleton in the first position.
A singleton in the second position can have 10 possible values, 0 through 9. If it’s a 0 there are 9 possible values for the triplet: 1011, 2022, 3033, …, 9099. If it’s anything else there are only 8 possible values for the triplet since the triplet cannot be 0: 2122, 3133, 4144, …, 9199. So there are 9 + (8 * 9) = 81 cases with the singleton in the second position.
The third and fourth positions work just like the second. So the grand total is 81 * 4 = 324.
If you plot the 9000 four-digit integers as a 100 x 90 grid of squares and color the integers with three same digits in red, an interesting pattern occurs:
There are 81 * 4 = 324 such integers.
There are 9000 four-digit integers from 1000 to 9999. Let’s refer to the digit that occurs three times as the triplet and the digit that occurs once as the singleton.
In the first (most significant) position there are 9 possible values for the singleton, 1 through 9. In each case there are also 9 possible values for the triplet. For example if the singleton was a 1, the triplets could be anything but a 1: 1000, 1222, 1333, …, 1999. So there are 9 * 9 = 81 cases with the singleton in the first position.
A singleton in the second position can have 10 possible values, 0 through 9. If it’s a 0 there are 9 possible values for the triplet: 1011, 2022, 3033, …, 9099. If it’s anything else there are only 8 possible values for the triplet since the triplet cannot be 0: 2122, 3133, 4144, …, 9199. So there are 9 + (8 * 9) = 81 cases with the singleton in the second position.
The third and fourth positions work just like the second. So the grand total is 81 * 4 = 324.
If you plot the 9000 four-digit integers as a 100 x 90 grid of squares and color the integers with three same digits in red, an interesting pattern occurs:
(If you zoom in, the four-digit number is printed inside each red square - not sure whether or not that will come through after Quora processes the image.)
Hope this helps!
Brain-List?

Answer:
81
Step-by-step explanation:
4 digit number: xxxy
x=1 y can be 0,2,3,4,5,6,7,8,9 ...9 possibility
x can be 1,2,3,4,5,6,7,8,9 ....9 too
9 x 9 = 81
My best guess, wish it's right.
evaluate the indefinite integral as a power series. ∫tan−¹(x) / x dx f(x) = c + [infinity]∑ n = 0 (....) what is the radius of convergence R?
R= ........
Answers
The indefinite integral of arctan(x)/x can be represented as a power series with a radius of convergence of 1.
The power series representation of the indefinite integral can be obtained by integrating the Taylor series expansion of arctan(x)/x term by term. The Taylor series expansion of arctan(x)/x is known to be x - x^3/3 + x^5/5 - x^7/7 + ..., which converges for |x| < 1.
Integrating term by term, we get the power series representation of the indefinite integral as c + x^2/2 - x^4/12 + x^6/30 - x^8/56 + ..., where c is the constant of integration.
The radius of convergence of this power series is determined by the convergence of the Taylor series expansion of arctan(x)/x, which is 1. Therefore, the radius of convergence for the power series representation of the indefinite integral is R = 1.
To learn more about power series click here: brainly.com/question/29896893
#SPJ11
Emily is buying a new mountain bike on layaway for $324 if she pays $54 each week how many weeks will it take Emily to pay for the mountain bike?
Answers
Answer: 6 weeks
Step-by-step explanation: $54 x 6 = $324
Gabriella earns $15 an hour and gets a 12% raise. With her raise, how much will she earn after working 40 hours?
Answers
Answer:
Step-by-step explanation:
15x 12%=1.8
so he earns $1.80 for the raise
so 15x1.8=27
So now he earns 27 for every hour.
27x40=1080
So now he earns $1080 in 40 hours.
15 + 1.80 , is 16.80. This will be the NEW amount she makes every hour.
16.80 x 40, $672. This amount will represent how much money she makes in fourth hours, AFTER her raise. Hope this helps :)
Find the perimeter. Simplify the answer.

Answers
Answer:
34p-16
Step-by-step explanation:
Perimeter of parallelogram
= 2(9p-10)+2(8p+2)
= 18p-20+16p+4
= 34p-16
Pleaseeeee helpppp !!!!!!!!!! Will mark Brianliest !!!!!!!!!!!!!!

Answers
Answer:
Square root of 56 so in simplest radical form 4 root 4
Step-by-step explanation:
hope this helped!
Choose the most appropriate answer.
"HEIGHT(50 inches)," "HEIGHT(50)," and "H(50)"all represent which of the
following?
O
A. The height of an object given a length of 50 inches.
B. The height of an object with area 50 inches.
C. The height of 50 inches.
Answers
Answer:
The answer its A:
Step-by-step explanation:
I hope its correct.
For the distribution in the following table, what is the 90th percentile?
X. C%
9 100%
8 80%
7 50%
6 25%
Answers
Answer:
the 90th percentile is 9.
The 90th percentile of the distribution is 9.
The 90th percentile of the distribution in the table is 9.
To find the 90th percentile, we need to look at the values of X and their corresponding cumulative percentages (C%). The 90th percentile is the value of X at which 90% of the data falls below.
Looking at the table, we can see that the value of X at the 90th percentile is 9, as it corresponds to a cumulative percentage of 100%. This means that 90% of the data falls below the value of 9.
Therefore, the 90th percentile of the distribution is 9.
To know more about percentile refer here:
https://brainly.com/question/4001098#
#SPJ11
what divided by 3 is -2
Answers
Answer:
-1.5
Step-by-step explanation:easy
8. Let ABCD be a parallelogram with A on top left, B on top right, D on bottom left and C on the bottom right. Prove that opposite sides of a parallelogram are congruent.
Answers
Answer:
Step-by-step explanation:
A parallelogram is a quadrilateral with four sides.
Given parallelogram ABCD, to prove that opposite sides of the parallelogram are congruent.
Join D to B, the diagonal of the parallelogram which is also a traversal.
So that;
<ABD = <BDC (alternate angle property)
<BAC = <ACD (alternate angle property)
Also, diagonals;
/AC/ = /BD/ (reflexive property)
Then;
ΔABD = ΔCBD (Angle-Side-Angle, ASA, property)
Thus;
/AB/ ≅ /CD/ (corresponding sides of congruent triangles are congruent)
/BC/ ≅ /AD/ (corresponding sides of congruent triangles are congruent)
Therefore, the opposite sides of the parallelogram ABCD are congruent.
Determine whether the triangles are similar. If so, choose the correct similarity statement and reason.
Answers
The ratio of the related flanks is not identical. Then the triangles are not similar.
What is the triangle?A triangle has three sides which are straight lines. The aggregation of the interior angle of the triangle is 180°.
If two triangles are equivalent, the ratio of the matching sides will not change.
The ratio is given as,
AE / EC = FA / FB
9 / 3 = 10 / 5
3 ≠ 2
The ratio of the related flanks is not identical. Then the triangles are not similar.
More about the triangle link is given below.
https://brainly.com/question/25813512
#SPJ9
The complete question is given below.

7x/3 < 2
Pls answer asp please and thank you
Answers
Answer:
x<6/7
Step-by-step explanation:
7x/3 < 2
7x < 6
x < 6/7
If you need to ask any questions, please let me know.
A mathematician works for hours per day and solves problems per hour, where and are positive integers and . One day, the mathematician drinks some coffee and discovers that he can now solve problems per hour. In fact, he only works for hours that day, but he still solves twice as many problems as he would in a normal day. How many problems does he solve the day he drinks coffee
Answers
The answer is that the mathematician solved 2k problems on the day he drank coffee.
Let's assume that the mathematician works for x hours a day and can solve y problems per hour. Also, the mathematician drinks some coffee and discovers that he can now solve z problems per hour. So, the mathematician works for n hours that day. We are given that:x*y = number of problems solved in a dayz * n = number of problems solved on the day he drank coffee
Then, we can write the equations:x*y = n * 2*z (he still solves twice as many problems as he would in a normal day)andx = n (he only works for n hours that day)Now, we need to simplify these equations to solve for the number of problems solved on the day he drank coffee. Here is how to do it:$$x*y = n * 2*z$$$$\frac{x*y}{x} = \frac{2*n*z}{x}$$$$y = 2 * \frac{n*z}{x}$$Since x, y, n, and z are all positive integers, we can say that the expression 2*n*z/x is also a positive integer. Therefore, we can write:$$\frac{2*n*z}{x} = k$$$$y = 2k$$where k is a positive integer.
Finally, the number of problems solved on the day he drank coffee is:y = 2k Therefore, the answer is that the mathematician solved 2k problems on the day he drank coffee.
To know more about equations refer to
https://brainly.com/question/29657983
#SPJ11
The price, s, of a mountain bike at Speed Cycling is $210 less than twice the price, d, of the same bike at Downhill Racing. The difference in price between the bike at Speed Cycling and Downhill Racing is $320. Which system of equations can be used to determine the price of the bike at each store?
A.
2s - d = 210
s - d = -320
B.
s - 2d = -210
s - d = -320
C.
2s - 2d = 210
s + d = 320
D.
s - 2d = -210
s - d = 320
Answers
Answer:
a
Step-by-step explanation:
hope this helps!! please mark brainliest
Consider the following expression.
5a+3+4b
Select all of the true statements below.
5a+3+4b is written as a product of three factors.
3 is a constant.
4 is a coefficient.
4b and 3 are like terms.
5a+3+4b is written as a sum of three terms.
None of these are true.

Answers
3 is a constant, 4 is the coefficient, 5a+3+4b is written as a sum of three terms are the true statements.
What is addition?The act of combining two or more items is known as addition. The process of computing the sum of two or more numbers in mathematics is called addition. It is a fundamental mathematical procedure that is frequently used in daily life. When we work with money, figure out our food bills, or figure out the time, we frequently employ addition. Mathematicians employ the action of addition to combine numbers. The sum of the given numbers is the outcome of addition, or the total of the inputted numbers.
Given that,
5a+3+4b
Select all of the true statements below.
5a+3+4b is written as a product of three factors.
3 is a constant.
4 is a coefficient.
4b and 3 are like terms.
5a+3+4b is written as a sum of three terms.
Therefore, 3 is a constant, 4 is the coefficient, 5a+3+4b is written as a sum of three terms are the true statements.
To know more about addition visit:
https://brainly.com/question/20658817
#SPJ9
The boxplots below show the distribution of test scores for two classes.
Which of the following statements is the most reasonable conclusion about the variability depicted in the boxplots? Check all that apply.
Group of answer choices
A. The median test scores are the same for both classes, so the variability is the same.
B. There is more variability in the test scores from class B because the IQR is larger.
C. The distance between Q1 and Q3 is greater for class B, so class B has a larger standard deviation.
D. There is more variability in the test scores from class B because the overall range is larger.
Answers
The correct statements are: B. There's more variability in the test scores from class B because the IQR is larger.
D. There is more variability in the test scores from class B because the overall range is larger.
What is variability?In mathematics, variability refers to the degree to which a data set deviates from its mean or central value. It is a measure of how spread out or dispersed the data values are within a set.
Explanation:
A. The median test scores are not same for both classes. Class A has a median of around 85 while class B has a median of around 75.
B. The IQR (interquartile range) represents the range between the first quartile (Q1) and the third quartile (Q3), which captures the middle 50% of the data. The IQR of class B is larger than that of class A, indicating that there is more variability in the test scores of class B.
C. The distance between Q1 and Q3 (i.e., IQR) is related to the standard deviation, but it is not a direct measure of it. Therefore, this statement is not accurate.
D. Range is the difference between the maximum and minimum values in a dataset. The overall range of class B is larger than that of class A, indicating that there is more variability in the test scores of class B.
To know more about median visit:
https://brainly.com/question/28060453
#SPJ1
An office has an area of 120m² and it is 12m wide. Write an equation to represent the area.
Answers
Answer:
Step-by-step explanation:
12y =120 y : the lenght
How do I find the y-intercept of a line with 2 points and slope?
I just need an equation to function on.
Answers
Answer:
y=mx+b
Step-by-step explanation:
B is the y intercept and m is the slope. Use y and x for the two points.
Use limit theorems to show that the following functions are continuous on (0, 1). (a) f(x) 2+1-2 (b) f(x) = 3 I=1 CON +0 =0 (e) f(x) 10 Svir sin (a) f(x) = #0 r=0
Answers
(a) The function f(x) = 2x + 1 − 2x² is continuous on (0, 1) using the limit theorems. (b) The function f(x) = 3(∑(n=1)^∞ 1/n²) + x is continuous on (0, 1) using the limit theorems.
a- To show that f(x) is continuous on (0, 1), we need to show that it is continuous at every point in (0, 1). Let x₀ be an arbitrary point in (0, 1), and let ε > 0 be given. We need to find a δ > 0 such that |f(x) − f(x₀)| < ε whenever |x − x₀| < δ and x ∈ (0, 1).
First, note that f(x) is a polynomial, so it is continuous on (0, 1) by definition. Moreover, we have:
|f(x) − f(x₀)| = |2x + 1 − 2x² − (2x₀ + 1 − 2x₀²)| = |2(x − x₀) − 2(x² − x₀²)|
Now, using the identity a² − b² = (a − b)(a + b), we can write:
|f(x) − f(x₀)| = |2(x − x₀) − 2(x − x₀)(x + x₀)| ≤ 2|x − x₀| + 2|x − x₀||x + x₀|
Since x + x₀ < 2 for all x, we have:
|f(x) − f(x₀)| ≤ 2|x − x₀| + 4|x − x₀| = 6|x − x₀|
Thus, we can choose δ = ε/6, and it follows that |f(x) − f(x₀)| < ε whenever |x − x₀| < δ and x ∈ (0, 1). Therefore, f(x) is continuous on (0, 1).
To show that f(x) is continuous on (0, 1), we need to show that it is continuous at every point in (0, 1). Let x₀ be an arbitrary point in (0, 1), and let ε > 0 be given. We need to find a δ > 0 such that |f(x) − f(x₀)| < ε whenever |x − x₀| < δ and x ∈ (0, 1).
First, note that the series ∑(n=1)^∞ 1/n² converges, so it has a finite limit L = ∑(n=1)^∞ 1/n². Thus, we can write:
|f(x) − f(x₀)| = |3L + x − (3L + x₀)| = |x − x₀|
Thus, we can choose δ = ε, and it follows that |f(x) − f(x₀)| < ε whenever |x − x₀| < δ and x ∈ (0, 1). Therefore, f(x) is continuous on (0, 1).
C-The function f(x) = ∑(n=0)^∞ xⁿ is continuous on (0, 1) using the limit theorems.
To show that f(x) is continuous on (0, 1), we need to show that it is continuous at every point in (0, 1). Let x₀ be an arbitrary point in (0, 1), and let ε > 0 be given. We need to find a δ > 0 such that |f(x) − f(x₀)| < ε whenever |x − x₀| < δ and x ∈ (0, 1).
Note that f(x) is an infinite geometric series with common ratio x, so we can write:
f(x) = 1 + x + x² + x³ + ... = 1/(1 − x)
Since 0 < x < 1, we have |f(x)| = |1/(1 − x)| < ∞. Moreover, we have:
|f(x) − f(x₀)| = |1/(1 − x) − 1/(1 − x₀)| = |(x₀ − x)/(1 − x)(1 − x₀)|
Now, suppose we choose δ = ε/2, and let |x − x₀| < δ. Then we have:
|(x₀ − x)/(1 − x)(1 − x₀)| ≤ 2|x₀ − x|/δ²
Thus, if we choose δ small enough so that 2/δ² < ε/(2|f(x)|), we get:
|f(x) − f(x₀)| < ε
Therefore, f(x) is continuous on (0, 1).
learn more about Limit Theorem here:
https://brainly.com/question/12207539
#SPJ4
Graph the function represented in the table on the coordinate plane
(-2,-3), (-1,-1), (0,1) (1,3) (2,5)

Answers
Hello, the graph sould be like this. Just remember, if you want to draw a graph, you should know the x and y state. x is from left and y is from right.