What is the x intercept of the line
A(0,2)
B(-7,0)
C(2,0)
D(0,-7)
PLZ I NEED THIS TO PASS MY CLASS
Btw the top is y the image was too long to fit

Answers
Explaining that is we’re th line crosses the y
Related Questions
Use the diagram to complete the statement.
measure of angle ECD

Answers
Answer:
∠ECD = 82°
Step-by-step explanation:
Alternate Interior Angles Theorem : when two parallel lines are cut by a transversal, the alternate interior angles are congruent. Alternate angles form a Z shape and are sometimes called "Z angles".
Therefore,
∠CDF = ∠GBC = 45°
∠CEF = ∠GAC = 53°
The sum of the interior angles of a triangle is 180°
⇒ ∠ECD + ∠CDF + ∠CEF = 180
⇒ ∠ECD + 45 + 53 = 180
⇒ ∠ECD = 180 - 45 - 53 = 82°
In ∆ABC
m<C be x\(\\ \tt\longrightarrow x+53+45=180\)
\(\\ \tt\longrightarrow x+98=180\)
\(\\ \tt\longrightarrow x=180-98\)
\(\\ \tt\longrightarrow x=82\)
Now
m<ECD and m<ACB are opposite hence equal
Given the following equation, what is the slope of the line -4y=-16x+24
Answers
Answer:
Slope = 4
Step-by-step explanation:
y=4x-6
Answer:
The slope is 4
Step-by-step explanation:
Cancel out the -4 so y is alone, divide -16 and 24 by -4. You'll get y=4x-6
The number in front of x is always the slope.
Alessia’s salary in 2022 was 26,000 after tax.
She spends 35% of her after tax salary on rent.
The rest is split between food, petrol and entertainment in the ratio 6:11:8
Work out how much alessia spent on entertainment in 2021
Answers
Alessia spent $5,408 on entertainment in 2021.
To determine how much Alessia spent on entertainment in 2021, we need to work backward from the given information about her salary in 2022.
Let's assume Alessia's salary in 2021 was the same as in 2022, which is $26,000 after tax.
Since Alessia spends 35% of her after-tax salary on rent, we can calculate her rent expenditure:
Rent = 35% × $26,000
= $9,100
The remaining amount is split between food, petrol, and entertainment in the ratio 6:11:8.
To determine the ratio's total parts, we sum the individual parts:
Total parts = 6 + 11 + 8 = 25
Next, we calculate the value of one part of the ratio:
One part = ($26,000 - $9,100) / 25
= $16,900 / 25
= $676
Now, we can calculate how much Alessia spent on entertainment in 2021, which is 8 parts of the ratio:
Entertainment expenditure = 8 × $676
= $5,408
For similar questions on entertainment
https://brainly.com/question/26767445
#SPJ8
is the equation 2x+y=4 and 2x^2+y=6 linear.. if so, how do i graph them?

Answers
Answer:
No, but you can graph them by converting to mx+b form
Step-by-step explanation:
The procedure for solving simultaneous linear equations now called Gaussian elimination appears in the ancient Chinese mathematical text Chapter Eight: Rectangular Arrays of The Nine Chapters on the Mathematical Art. Its use is illustrated in eighteen problems, with two to five equations.[4]
Systems of linear equations arose in Europe with the introduction in 1637 by René Descartes of coordinates in geometry. In fact, in this new geometry, now called Cartesian geometry, lines and planes are represented by linear equations, and computing their intersections amounts to solving systems of linear equations.
The first systematic methods for solving linear systems used determinants, first considered by Leibniz in 1693. In 1750, Gabriel Cramer used them for giving explicit solutions of linear systems, now called Cramer's rule. Later, Gauss further described the method of elimination, which was initially listed as an advancement in geodesy.[5]
In 1844 Hermann Grassmann published his "Theory of Extension" which included foundational new topics of what is today called linear algebra. In 1848, James Joseph Sylvester introduced the term matrix, which is Latin for womb.
Linear algebra grew with ideas noted in the complex plane. For instance, two numbers w and z in {\displaystyle \mathbb {C} }\mathbb {C} have a difference w – z, and the line segments {\displaystyle {\overline {wz}}}{\displaystyle {\overline {wz}}} and {\displaystyle {\overline {0(w-z)}}}{\displaystyle {\overline {0(w-z)}}} are of the same length and direction. The segments are equipollent. The four-dimensional system {\displaystyle \mathbb {H} }\mathbb {H} of quaternions was started in 1843. The term vector was introduced as v = x i + y j + z k representing a point in space. The quaternion difference p – q also produces a segment equipollent to {\displaystyle {\overline {pq}}.}{\displaystyle {\overline {pq}}.} Other hypercomplex number systems also used the idea of a linear space with a basis.
Arthur Cayley introduced matrix multiplication and the inverse matrix in 1856, making possible the general linear group. The mechanism of group representation became available for describing complex and hypercomplex numbers. Crucially, Cayley used a single letter to denote a matrix, thus treating a matrix as an aggregate object. He also realized the connection between matrices and determinants, and wrote "There would be many things to say about this theory of matrices which should, it seems to me, precede the theory of determinants".[5]
Benjamin Peirce published his Linear Associative Algebra (1872), and his son Charles Sanders Peirce extended the work later.[6]
The telegraph required an explanatory system, and the 1873 publication of A Treatise on Electricity and Magnetism instituted a field theory of forces and required differential geometry for expression. Linear algebra is flat differential geometry and serves in tangent spaces to manifolds. Electromagnetic symmetries of spacetime are expressed by the Lorentz transformations, and much of the history of linear algebra is the history of Lorentz transformations.
The first modern and more precise definition of a vector space was introduced by Peano in 1888;[5] by 1900, a theory of linear transformations of finite-dimensional vector spaces had emerged. Linear algebra took its modern form in the first half of the twentieth century, when many ideas and methods of previous centuries were generalized as abstract algebra. The development of computers led to increased research in efficient algorithms for Gaussian elimination and matrix decompositions, and linear algebra became an essential tool for modelling and simulations.[5]
Vector spaces
Main article: Vector space
Until the 19th century, linear algebra was introduced through systems of linear equations and matrices. In modern mathematics, the presentation through vector spaces is generally preferred, since it is more synthetic, more general (not limited to the finite-dimensional case), and conceptually simpler, although more abstract.
A vector space over a field F (often the field of the real numbers) is a set V equipped with two binary operations satisfying the following axioms. Elements of V are called vectors, and elements of F are called scalars. The first operation, vector addition, takes any two vectors v and w and outputs a third vector v + w. The second operation, scalar multiplication, takes any scalar a and any vector v and outputs a new vector av. The axioms that addition and scalar multiplication must satisfy are the following. (In the list below, u, v and w are arbitrary elements of V, and a and b are arbitrary scalars in the field F.)[7]
Bobby has d more than 3 times the number of baseball cards as Michael. Michael has m baseball cards. Write an expression to represent the situation
Answers
The expression representing the situation is B = 3M + d, where B represents the number of baseball cards Bobby has, M represents the number of baseball cards Michael has, and d represents the additional amount that Bobby has compared to three times the number of cards Michael has.
Step 1: Assign variables.
Let's assign the variable "B" to represent the number of baseball cards Bobby has and the variable "M" to represent the number of baseball cards Michael has.
Step 2: Understand the relationship.
According to the given information, Bobby has "d" more than 3 times the number of baseball cards as Michael. This means that Bobby's number of baseball cards can be calculated by taking 3 times the number of cards Michael has and adding "d" to it.
Step 3: Create the expression.
To represent the situation, we can write the expression as: B = 3M + d.
Step 4: Interpret the expression.
In this expression, "3M" represents 3 times the number of baseball cards Michael has, and "d" represents the additional amount that Bobby has compared to that.
Therefore, the expression B = 3M + d represents the situation where Bobby has "d" more than 3 times the number of baseball cards as Michael. This expression allows us to calculate Bobby's number of cards based on the given relationship between their card counts.
To know more about relationship , visit:
https://brainly.com/question/26421194
#SPJ11
How do you find the vertex form of y=3x^25x3 by completing the quare? can you explain ALL the tep?
Answers
Answer:
Below
Step-by-step explanation:
To complete the square, the leading x^2 coefficient needs to be = 1 , so factor out a 3 to get
y = 3 ( x^2 + 5/3x ) +3 (I assumed it was a + sign between the terms)
Then take 1/2 of the 5/3 ( 5/6 ) , square it (25/36) , add it to the parentheses.... then subtract the amount you added (3 * 25/36) by doing this..... to have this :
y = 3 ( x^2 + 5/3 x + 25/36) - 3 * 25/36 +3 then simplify to
y = 3 ( x + 5/6)^2 + 11/12 Done.
having problems with geometry homework, help me please
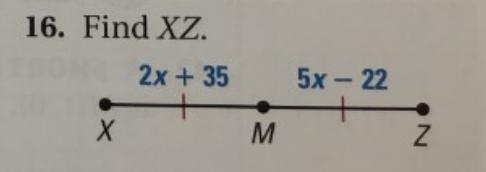
Answers
Just equal the two equations together and solve
Brainliest?
Answer:
\(XZ=146\)
Step-by-step explanation:
Since \(M\) is the midpoint of segment \(XZ\):
\(XM+MZ=XZ\)
\(XM=MZ\)
Identify your known values:
\(XM=2x+35\\MZ=5x-22\\\)
Solve for \(x\):
\(2x+35=5x-22\)
Subtract \(35\) from both sides of the equation:
\(2x=5x-57\)
Subtract \(5x\) from both sides of the equation:
\(-3x=-57\)
Divide by the coefficient of \(x\), which is \(-3\):
\(x=19\)
Substitute:
\(XM=2(19)+35\\MZ=5(19)-22\)
Solve:
\(XM=73\\MZ=73\)
Again, we know:
\(XM+MZ=XZ\)
Therefore:
\(XZ=73+73\)
Solve:
\(XZ=146\)
Line AB contains points A(4, 5) and B(9, 7). What is the slope of AB ?
Answers
Answer:
2/5 or 2 over 5
Step-by-step explanation:
y2-y1 over x2-x1 gives you your slope
in its simplest form, kanban consists of a whiteboard divided into multiple columns. what are they titled?
Answers
The correct option for whiteboard of the Kanban are-
b) Planned; e) Done; f) WIP
Explain the term Kanbanboard?The work that needs to be done, that work that is being done, and the work that has been finished are all displayed on a Kanban Board.
It's a graphic representation of a person's, a team's, or a department's value stream, which has been diagrammed on a board, a wall, or specifically designed Kanban software.The purpose of the Kanban technique applied to knowledge management is the same as it was in manufacturing even though it was developed as a stock management tool in Toyota manufacturing: better visualize work, restrict work progress, optimize flow, and uncover improvement opportunities.Thus, the more visible a Kanban board is, the better; optimum outcomes are likely to be achieved when a team can always see it.
To know more about the Kanbanboard, here
https://brainly.com/question/19091903
#SPJ4
The complete question is-
In its simplest form, Kanban consists of a whiteboard divided into multiple columns. What are they titled?
a) In Queue
b) Planned
c) Opened Ticket
d) Delayed
e) Done
f) WIP
Give the vector equation of the line passing through P and P=(4,3),Q=(1,0)
Answers
The vector equation of the line passing through P(4,3) and Q(1,0) is r = (4 + 3t, 3 + 3t), where t is a parameter.
To find the vector equation of the line passing through points P(4,3) and Q(1,0), we need to determine the direction vector of the line and a point on the line.
The direction vector of the line can be obtained by subtracting the coordinates of one point from the coordinates of the other point. In this case, we can subtract the coordinates of point Q from the coordinates of point P to get the direction vector:
Direction vector = PQ = P - Q = (4, 3) - (1, 0) = (4 - 1, 3 - 0) = (3, 3)
Now, let's choose point P(4,3) as a point on the line.
The vector equation of a line passing through a given point P and with a direction vector d can be written as:
r = P + td
where r is the position vector of any point on the line, t is a parameter, and d is the direction vector.
Substituting the values we have:
r = (4, 3) + t(3, 3)
Expanding the equation:
r = (4 + 3t, 3 + 3t)
Therefore, the vector equation of the line passing through P(4,3) and Q(1,0) is r = (4 + 3t, 3 + 3t), where t is a parameter.
Learn more about position vector here:
https://brainly.com/question/31289161
#SPJ11
Tony is opening a pizza restaurant and needs to determine the amounts of ingredients he will use in his pizzas. He wants the amount of dough for a medium pizza to be times the amount of dough for a small pizza. And, he wants the amount of dough for a large pizza to be 3/2 times the amount of dough for a small pizza. Also, the amount of dough used for one large pizza should be 5/2 equal to the amount of dough used for one medium and one small pizza. So, he needs to determine how much dough to use for a small pizza. Use this information to complete the following tasks.
Now, use opposite operations on the equation from part B to move one of the terms so they are both on the same side of the equal sign.
Please it worth 43 points
Answers
The equation that represents this situation while the variable s representing the amount of dough needed , for a small pizza is (5/2)S = (3/2)S + S .
In the question ,
it is given that
amount of dough for a medium pizza is 3/2 times the amount of dough for small pizza ,
let the amount of dough required for small pizza = S
let the amount of dough required for large pizza = L
let the amount of dough required for medium pizza = M
So , M \(=\) (3/2)S
and amount of dough for a large pizza is 5/2 times the amount of dough for small pizza ,
that is
L \(=\) (5/2)S
amount of dough used for one large pizza is equal to the amount of dough used for one medium and one small pizza ,
that is L \(=\) M \(+\) S .
Substituting the value of L and S , we get
(5/2)S \(=\) (3/2)S + S
We have a linear equation that is true for all S , there is no unique solution to this equation .
Therefore , The equation that represents this situation is (5/2)S = (3/2)S + S .
The given question is incomplete , the complete question is
Tony is opening a pizza restaurant and needs to determine the amounts of ingredients he will use in his pizzas. He wants the amount of dough for a medium pizza to be 3/2 times the amount of dough for a small pizza. And, he wants the amount of dough for a large pizza to be 5/2 times the amount of dough for a small pizza. Also, the amount of dough used for one large pizza should to be equal to the amount of dough used for one medium and one small pizza. So, he needs to determine how much dough to use for a small pizza. Use this information to complete the following tasks.
Write an equation to represent this situation while the variable s representing the amount of dough needed , for a small pizza .
Learn more about Equation here
https://brainly.com/question/17026235
#SPJ1
Please help me with 47 and 48

Answers
Answer:
42. -1
48. 2
Step-by-step explanation:
Answer:
-1
2
Step-by-step explanation:

When 1,250 superscript three-fourths is written in its simplest radical form, which value remains under the radical?
Answers
The number that still remains under the radical when the expression is in its simplest form is 8.
What is a radical?
A radical refers to a root form. In this case, we can write this number as; 1,250^3/4.
If we try to simplify this in line with the laws of indicies, we have; 4√(1250)^3. If we simpify further, we obtain; (125)4√8.
Thus, the number that still remains under the radical when the expression is in its simplest form is 8.
Learn more about radical forms:https://brainly.com/question/3008670
#SPJ4
3. Nathan has a car loan of $2,000, a mortgage balance of $150,000 and
student loans of $15,000. If Nathan's debt ratio is 80%, what is Nathan's
net worth?
Answers
To calculate Nathan's net worth, we need to determine his total liabilities (debt) and subtract that from his total assets. The debt ratio tells us that Nathan's liabilities are 80% of his total net worth.
Total liabilities = Car loan + Mortgage + Student loans = $2,000 + $150,000 + $15,000 = $167,000
Nathan's net worth = Total assets = Total liabilities / Debt ratio = $167,000 / 0.8 = $208,750
So, Nathan's net worth is $208,750.
HELP ME WITH THESE TWO

Answers
12. A. 4 proton and 4 neutrons
mark me brianliest if i helped! :)
Determine the density of a proton. For a sphere \( V=\left(\frac{4}{3}\right) \pi r^{3} \). Express the density to two significant figures.
Answers
The density is 1.7 x 10^-27 kg/m^3.
The density of a proton can be determined by calculating its mass and volume. Given the volume of a sphere, the density of a proton can be expressed to two significant figures.
To determine the density of a proton, we need to calculate its mass and volume. The mass of a proton is approximately 1.67 x 10^-27 kilograms. The volume of a sphere is given by the formula V = (4/3)πr^3, where r is the radius. Since a proton is considered a point particle, it does not have a defined radius. Therefore, we assume the radius to be extremely small, close to zero. Substituting this value into the volume equation, we get V = (4/3)π(0)^3 = 0. However, the mass of the proton remains unchanged. Thus, the density of a proton is approximately 1.67 x 10^-27 kilograms per cubic meter. Rounded to two significant figures, the density is 1.7 x 10^-27 kg/m^3.
For more information on protons visit: brainly.in/question/16676620
#SPJ11
Question 1 (1 point)
What integer represents a rise in temperature of 19°?
O a -|-191
Ob
-19
Oc
19
Od
-|19|
Answers
The integer which represents the rise in temperature of 19° is -|19|
Positive, negative, and zero numbers all fall under the category of integers. The word "integer" is a Latin word that signifies "whole" or "intact." Therefore, fractions and decimals are not considered to be integers.
A number without a decimal or fractional element is known as an integer, which encompasses both positive and negative numbers, including zero. The following are some examples of integers: -5, 0, 1, 5, 8, 97, and 3,043. Z denotes a collection of integers,
hence the correct form is answered.
Learn more about Integers here:
brainly.com/question/17695139
#SPJ9
A triangular pyramid has a base with an area of 21.8 square meters, and lateral faces with bases of 7.1 meters and heights of 9 meters. Enter an expression that can be used to find the surface area of the triangular pyramid.
Answers
Answer:
Step-by-step explanation:
A triangular pyramid has a base with an area of 21.8 square meters, and lateral faces with bases of 7.1 meters and heights of 9 meters. Enter an expression that can be used to find the surface area of the triangular pyramid.
The expression is written as:
Surface Area = Area of the base + 1/2( Perimeter × Slant height)
Complete the table. In the row with X as the input write the rule as an algebraic expression for the output then complete the last row of the table using the rule. Express the values in your answers as decimals

Answers
The last two rows of the table should be completed as follows:
Input Output
8 22.80
10 28.50
What is algebraic expression?An algebraic expression is a mathematical phrase that contains numbers, variables, and operations. It is used to represent a single quantity or value, and can be written in terms of one or more variables.
The rule given is an algebraic expression, x, which is the input, multiplied by 2.85, which is the output. Using this information, we can determine the cost of 10 muffins.
To find the cost of 10 muffins, we can use the algebraic expression given. First, we will multiply 10, the number of muffins, by 2.85, the cost of one muffin. This gives us a total of 28.50. Therefore, the cost of 10 muffins is 28.50.
Using this same rule and process, we can also determine the cost of any number of muffins. For example, if we want to know the cost of 15 muffins, we can simply multiply 15 by 2.85, giving us a total of 42.75.
For more questions related to numbers
https://brainly.com/question/24644930
#SPJ1
Can someone help me solve these two questions?

Answers
Answer:
13. P(-8,2)
14. M(4,-5)
The ratio of men to women working for a company is 5 to 4. If there are 234 employees total, how many women work for the company?
Answers
Answer:
104
Step-by-step explanation:
5 to 4 equals 9
divide 234 by 9 and you get 26
26 times 5 is 130
and 26 times 4 is 104
so 130 to 104 adding up gives you 234
and the number of women employees would be 104
3.
For what value of x will 3x + 4 = x-6 be a true
statement?
A. x = -5
B. x=-
C. r= -1
D. x =
x=-

Answers
Answer:
A
Step-by-step explanation:
3x +4 = x-6
3x -x = -6 -4
2x = -10
x = -10/2 = -5
For the given expression identify the terms like terms coefficient and constant terms then simplify the expression -8c+-c+1
Answers
Answer:
The simplified expression is : -9c +1
Step-by-step explanation:
The like terms are -8c and -c
The constant term is 1
The simplified expression is :
-8c + -c + 1 = -9c +1
Use the following diagram to solve the problem
Solve for x.
A.13
B.17
C.47
c.34

Answers
Answer:
B
Step-by-step explanation:
The exterior angle of a triangle is equal to the sum of the 2 opposite interior angles.
94° is an exterior angle of the triangle, thus
60 + 2x = 94 ( subtract 60 from both sides )
2x = 34 ( divide both sides by 2 )
x = 17 → B
Study Guide:
What are the assumptions (or conditions) required for the Intermediate Value Theorem?
Answers
The Intermediate Value Theorem states that for any value c between the function's values at the endpoints (f(a) and f(b)), there exists a value x in the interval [a, b] such that f(x) = c.
The assumptions (or conditions) required for the Intermediate Value Theorem are:
1. The function is continuous: The function must be continuous on the closed interval [a, b]. This means that there are no breaks, jumps, or holes in the graph of the function within the given interval.
2. The interval is closed and bounded: The interval [a, b] must be a closed interval, meaning it includes both endpoints a and b. Additionally, the interval must be bounded, meaning the function has a maximum and a minimum value within the interval.
By satisfying these two assumptions, the Intermediate Value Theorem states that for any value c between the function's values at the endpoints (f(a) and f(b)), there exists a value x in the interval [a, b] such that f(x) = c.
Learn more about function here,
https://brainly.com/question/16634496
#SPJ11
3. A leaking tap drips water at 0,5 ml/sec. Convert this rate to l/h.
Answers
Answer: 1.8 L/h
Step-by-step explanation:
To convert the rate of water dripping from a tap from millilitres per second (ml/sec) to litres per hour (L/h), we need to use conversion factors.
Step 1:
First, let's convert the rate from millilitres per second to litres per second.
There are 1000 millilitres in a litre, so we can divide the rate in millilitres per second by 1000 to get the rate in litres per second:
\(\LARGE \boxed{\textsf{0.5 ml/sec $\div$ 1000 = 0.0005 L/sec}}\)
Step 2:
We can convert the rate from litres per second to litres per hour. There are 3600 seconds in an hour, so we can multiply the rate in litres per second by 3600 to get the rate in litres per hour:
\(\LARGE \boxed{\textsf{0.0005 L/sec $\times$ 3600 = 1.8 L/h}}\)
Therefore, the rate of water dripping from the tap is 1.8 L/h.
----------------------------------------------------------------------------------------------------------
In a class of 36 students, 29 do mathematics and 20 do chemistry. If 5 students do neither, how many students do chemistry but not mathematics?
Answers
Answer:
2 students do Chemistry, but not Mathematics
Step-by-step explanation:
2 students do Chemistry, but not Mathematics
*View attached table*
Hope this helps!

The temperature startedat 10 degrees F. The temperature dropped 5
degrees every hour. What was the temperature after 3 hours?
Answers
Answer:
-5FStep-by-step explanation:
10-5x3=-5 F
what is (13X + 9k)+(17x +6k), simplified?
Answers
Answer:
(45x)
Step-by-step explanation:
(13x+9x) + (17x+6x)
(22x) + (23x)
(45x)
// have a great day //
this is extra credit . solve for X

Answers
Answer:
x = - 15
Step-by-step explanation:
The sum of the 3 angles in a triangle = 180°
Sum the 3 given angles and equate to 180, that is
35 - 5 - 8x - 2x = 180 ( simplify left side )
30 - 10x = 180 ( subtract 30 from both sides )
- 10x = 150 ( divide both sides by - 10 )
x = - 15