What is the velocity of an airplane traveling 4500 miles West over 10 hours?
Answers
The velocity of the airplane traveling 4500 miles West over 10 hours is 450 miles per hour. This calculation provides the speed at which the airplane is moving in the given direction.
To calculate the velocity of an airplane traveling 4500 miles West over 10 hours, we need to divide the distance traveled by the time taken.
Velocity is defined as the rate at which an object moves in a specific direction, and it is given by the formula:
Velocity = Distance / Time
In this case, the distance traveled by the airplane is 4500 miles West, and the time taken is 10 hours. Let's calculate the velocity:
Velocity = 4500 miles / 10 hours
Dividing 4500 by 10, we find:
Velocity = 450 miles per hour
Therefore, the velocity of the airplane traveling 4500 miles West over 10 hours is 450 miles per hour. This calculation provides the speed at which the airplane is moving in the given direction.
Learn more about velocity here
https://brainly.com/question/31481665
#SPJ11
Related Questions
A juice box has 20% more Juice new packaging the original packaging how 12 fluid ounces how much does the new packaging hold
Answers
Answer:
a juice bo has 20% more juice than the original package. the original package holds 12 ounces.
first find what 100% of 12 is. 12 obvi. then divide 12 by 10 to get what 10% is. 10% of 12 is 1.2 so multiply 1.2 by 2 which is 2.4, and thats 20% of 12.
now add 2.4 to 12, and you get 14.4, how much the new juice box holds
Mark the focus of the parabola you are going to create at F(6, 4). Draw a horizontal line that is 6 units below the focus. This line will be the directrix of your parabola. What is the equation of the line?
Answers
Answer: y=-2
Step-by-step explanation:

Based on the location of the line and the focus of the parabola, the equation of the line will be y = -2.
What is the equation of the line?The line is a horizontal line which means that the primary focus will be on the y axis.
The focus of the parabola is at F(6, 4) and the line is to be 6 units below this focus which means that the line on the y axis will be at:
= 4 - 6
= -2
This leaves the formula of the line as y = -2.
Find out more on parabolas at https://brainly.com/question/4148030.
HELP ASAP PLEASE!!
full work shown gets brainliest!!
What is the product of 8 radical 5and 2 radical 30 in simplest radical form?
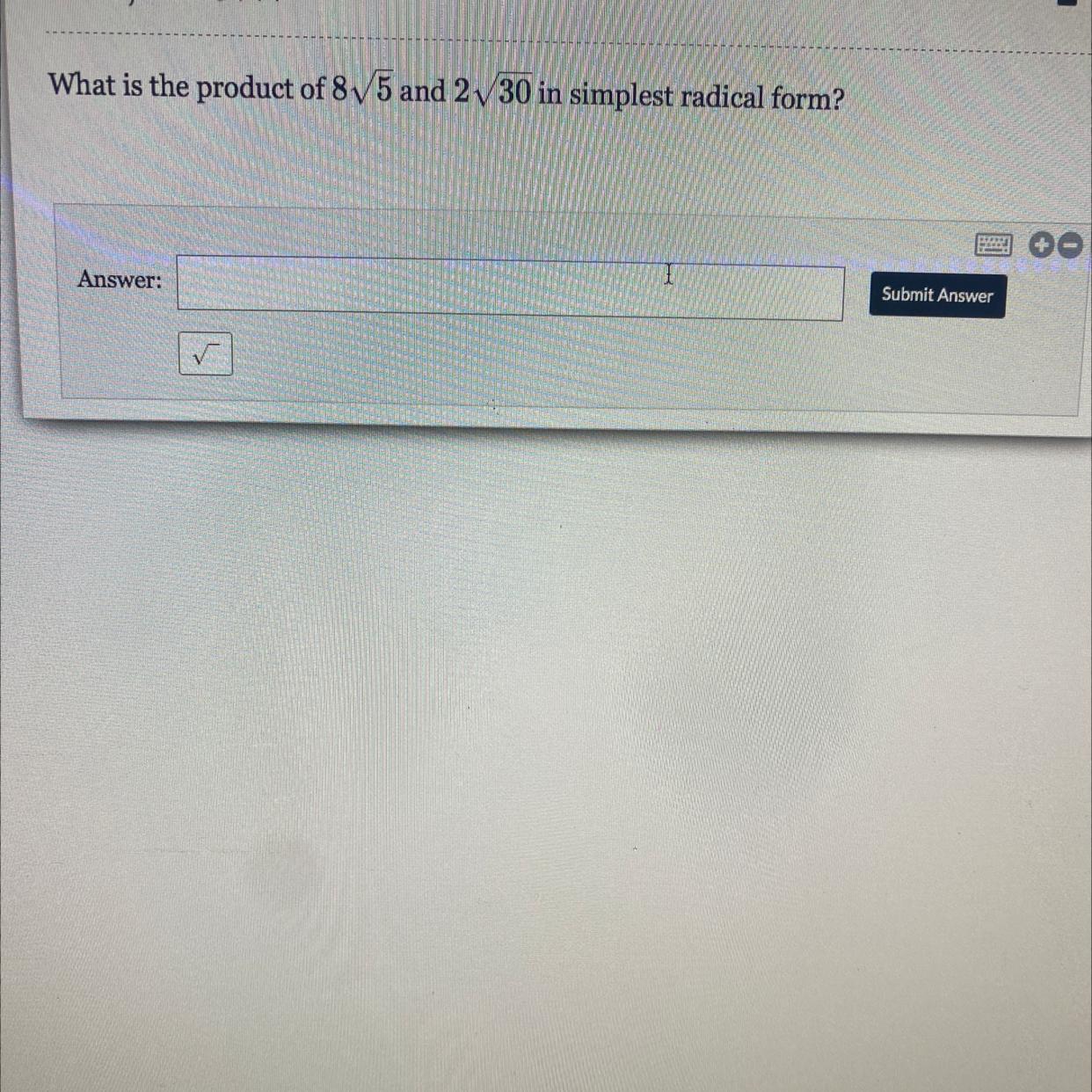
Answers
Answer:
= 40√6
Step-by-step explanation:
least common multipler of 8,2:8
What is the length of a diagonal of a rectangular picture whose sides are 12" x 17" round to the nearest 10th of an inch
Answers
12^2 + 17^2 = 485
so c^2=485
so c=22.0 inches
Carlos burns 75 calories for every 15 minutes he walks how many calories will Carlos burn if he walks for 45 minutes
Answers
how many days could a 60kg deer survive without food at -20 degrees - has 5kg of fat
18 days
Answers
The survival time of a 60kg deer without food at -20 degrees Celsius depends on various factors, including its age, sex, and physical condition. However, assuming the deer is healthy and has 5kg of fat, it could potentially survive for around 30 to 50 days without food.
The exact survival time can vary depending on several factors, such as the deer's level of physical activity, environmental conditions, and how much energy it is expending to stay warm in the cold temperature. Additionally, if the deer is able to find sources of water, this can also increase its chances of survival.
It's important to note that this is just an estimate and that the actual survival time may vary. If the deer is injured or sick, its chances of survival may be reduced, and it may not be able to survive as long without food.
Learn more about “20 degrees Celsius “ visit here;
https://brainly.com/question/827047
#SPJ4
Complete Question
How many days could a 60kg deer survive without food at -20 degrees Celsius if it has 5kg of fat?
A triangle has two sides of length 6 and 19. What is the largest possible whole-number length for the third side?
Answers
Answer: 18
Step-by-step explanation:
If 19 Is hypotenuse and 6 is one of the sides
Given the equation startfraction 2 x 2 over y endfraction = 4 w 2 what is the value of x? x = y w y minus 1 x = 2 y w y minus 1 x = 2 y w y minus 2 x = 4 y w 2 y minus 2
Answers
The value of x is 2yw + y - 1 for the given equation 2x + 2/y = 4w + 2.
According to the given question.
We have an equation
2x + 2/y = 4w + 2
Since, we have to find the value of x for the given equation
2x + 2/y = 4w + 2
Thereofore,
2x + 2/y = 4w + 2
⇒ 2(x + 1)/y = 2(2w + 1) (taking 2 common from both the sides)
⇒ (x + 1)/y = 2w + 1
⇒ (x + 1) = y(2w + 1) (multiplying both the sides by y)
⇒ x + 1 = 2yw + y
⇒ x = 2yw + y - 1 ( subtracting 1 both the sides)
Hence, the value of x is 2yw + y - 1 for the given equation 2x + 2/y = 4w + 2.
Find out more information about equation here:
https://brainly.com/question/14686792
#SPJ4
a city has 8984 recycle bins the city gives half of the recycle bins to its citizens the rest of the recycle bins are divided into 25 groups for city parks .How many recycle bins are left over?
Answers
Answer:
7867867867878678
Step-by-step explanation:
uyityuityuituityuityuityui
write 600 as a product of a prime factor give your answer in index form
Answers
Answer:This is problems on common factors.
(a) 600 = 2 × 2 × 2 × 3 × 5 × 5
= 2³ˣ 3 ˣ 5²
(b) The highest common factors could be calculated using factors methods and the divisional methods.
Here we go.
(i) 600 = 2³ ˣ 3 ˣ 5²
1050 = 2 ˣ 3 ˣ 5² ˣ 7, the highest common factor HCF will be
HCT = 2 ˣ 3 ˣ 5²
= 150.
The divisional methods.
600) 1050 ( 1
- 600
------
450 ) 600 ( 1
- 450
------
150 ) 450 ( 3
- 450
------
000
So the answer is 150, the principle is that you continue to divide and subtract until you arrive at zero.
Answer = 150
If this is incorrect you should report my answer... Hope this was helpful... Stay safe and have a great weekend!!! :D
i need help whatsb the answer

Answers
Answer:Simplify the expression.
Exact Form:
35
8
Decimal Form:
4.375
Mixed Number Form:
4 3/8
Step-by-step explanation:
this is the answer
How do I find the surface area of of rectangle
Answers
Determine whether the sequence an = arctan(14n^18) converges or diverges. If it converges, find the limit. Converges (y/n): ____.
Limit (if it exists, blank otherwise): ____.
Answers
The sequence an = arctan(14n¹⁸) diverges as n approaches infinity.
Converges (y/n): No (n)
Limit (if it exists, blank otherwise): ____
This is because the arctan function has a bounded range between \(-\frac{\pi}{2}\) and \(\frac{\pi}{2}\), and the argument of the arctan function, 14n¹⁸, grows without bound.
Here is the explanation :
To determine whether the sequence an = arctan(14n¹⁸) converges or diverges, we need to analyze the behavior of the sequence as n approaches infinity.
Let's consider the limit of the sequence as n approaches infinity:
\(\[\lim_{n\to\infty} \arctan(14n^{18})\]\)
As n approaches infinity, the term 14n¹⁸ also approaches infinity. However, the arctan function has a bounded range between \(-\frac{\pi}{2}\) and \(\frac{\pi}{2}\).
Since the argument of the arctan function, 14n¹⁸, grows without bound, the arctan function will continue to oscillate between \(-\frac{\pi}{2}\) and \(\frac{\pi}{2}\) as n increases.
Therefore, the sequence an = arctan(14n¹⁸) diverges as n approaches infinity.
Converges (y/n): No (n)
Limit (if it exists, blank otherwise): ____
To know more about arctan function refer here :
https://brainly.com/question/30198943#
#SPJ11
its in the photo which one is the answer

Answers
Answer:
number 3 is the answer
Step-by-step explanation:
hope u understand
HELPPP URGENT URGENT HELP PLEASE!
in the diagram below what is the objects surface area?
if you answer this not only you will get hella points you will be considered SUPERIOR and a GOD OF BRAINLY

Answers
Answer:
Surface Area = 4928 ft^2
Step-by-step explanation:
Easy way -
First find the area of each face i.e.
56 * 20 = 1120
65 * 20 = 1300
33 * 20 = 660
2 * (1/2 * 56 * 33) = 1848
Total = 4928 ft^2
A trucker handed in a ticket at a toll booth showing that in 2 hours she had covered 159 on a toll road with a posted speed limit of 65 mph. The trucker was cited for speeding. Why?
Answers
Answer:
overspeeding,
see if we calculate the speed or average speed,
it would be 159/2 which would be 79.5mph,
so as posted speed was 65mph, but the average speed was 79.5mph(Meaning most of the time she would have been above 65 mph), So,
She would have been charged with overspeeding
HOPE IT HELPS
BYE!
Triangle BCD, with vertices B(4,-7), C(6,-8), and D(7,-2), is drawn on the coordinate
grid below.
S
Answer: A =
6
7
D
9
What is the area, in square units, of triangle BCD?
units
Submit Answer
K

Answers
Answer: The area is 6.5
If x and y are any random variables with e(x) = 5, e(y) = 6, e(xy) = 21, v(x) = 9 and v(y) = 10, then the relationship between x and y is a:______.
Answers
The relationship between x and y is a strong negative relationship.
For this question, we need to determine the correlation coefficient,
Thus,
The correlation coefficient
= (21 - 5*6)/ \(\sqrt{9 * 10}\)
= -0.948
The above answer is too close to -1. Therefore correlation coefficient is a strong negative.
To determine more on correlation coefficient, use:
brainly.com/question/27226153
#SPJ4
Write a declaration for a variable rate_of_pay that can hold values like 11.50 or 12.75.
Answers
Float rate_of_pay a declaration for a variable rate_of_pay that can hold values like 11.50 or 12.75.
What is float rate_of_pay?
In contrast to fixed (or unchangeable) interest rates, floating interest rates change on a regular basis. Companies that offer credit cards and mortgages frequently use floating rates. Floating rates follow the market, a benchmark interest rate, an index, or both.Is a fixed or floating rate preferable?
In a rising rate environment, banks offer fixed rate loans at a higher rate than variable rate loans in order to profit more from the latter when rates rise. Fixed rate loans may have interest rates that are 300–350 basis points higher than floating rate loans.float rate_of_pay
rate_of_pay = 11.50, 12.75;
Learn more about Float rate_of_pay
brainly.com/question/14128610
#SPJ4
a notebook is 8 inches tall and 10 inches wide what is its area?
Answers
Answer:
i think 18
Step-by-step explanation:
Determine the inverse of the function f (x) = 3(x − 4)^2 + 5.
Answers
Step-by-step explanation:
since g(f(x)) = x g (f (x) )= x, f - 1 (x) = 5x3 + 43 f - 1 (x) = 5 x 3 + 4 3
The inverse of the given function \(f(x) = 3(x-4)^{2} +5\) is \(f^{-1} (x) = \sqrt{\frac{x-5}{3} } +4\).
What is the inverse of a function?An inverse function or an anti function is defined as a function, which can reverse into another function. In simple words, if any function “f” takes x to y then, the inverse of “f” will take y to x. If the function is denoted by ‘f’ or ‘F’, then the inverse function is denoted by \(f^{-1}\) or \(F^{-1}\).
According to the given equation.
We have a function.
\(f(x) = 3(x-4)^{2} +5\)
The above function can be written as
\(y = 3(x-4)^{2} +5\)
Write the above function for x.
\(\implies y -5 = 3(x-4)^{2}\)
\(\implies \frac{y-5}{3} = (x-4)^{2}\)
\(\implies \sqrt{\frac{y-5}{3} } =x-4\)
\(\implies \sqrt{\frac{y-5}{3} } +4=x\)
\(0r\ x = \sqrt{\frac{y-5}{3}}+4\)
Replace \(x\) by \(f^{-1}(x)\) and \(y\) by \(x\).
We get
\(f^{-1} (x) = \sqrt{\frac{x-5}{3} } +4\)
Hence, the inverse of the given function \(f(x) = 3(x-4)^{2} +5\) is \(f^{-1} (x) = \sqrt{\frac{x-5}{3} } +4\).
Find out more information about the inverse of the function here:
https://brainly.com/question/2541698
#SPJ2
what is the quotient?
- 4/5 divided by 2
o -1 2/5
o - 2/5
o 1/2
o 1 3/5 ✨
Answers
\( - \frac{4}{5} \div 2 = - \frac{4}{5} \times \frac{1}{2} = - \frac{2 }{5} \\ \)
So the second one is the correct answer.
Answer:
- 2/5
Step-by-step explanation:
divide
add - sign
hope this helps
You spin the spinner once.
What is P(odd or divisor of 9)? Enter your answer as a percentage.
Answers
The probability of getting an odd number or a divisor of 9 when spinning the spinner once is 75%
To calculate the probability of getting an odd number or a divisor of 9 when spinning the spinner once, we need to first identify the possible outcomes.
The spinner can have 8 possible outcomes, which are: 1, 2, 3, 4, 5, 6, 9, and 10. Out of these outcomes, we have 4 odd numbers (1, 3, 5, and 9) and 2 divisors of 9 (9 and 10).
To calculate the probability, we need to add the probabilities of getting an odd number and a divisor of 9, and then subtract the probability of getting both an odd number and a divisor of 9 (since that would be counted twice otherwise).
P(odd or divisor of 9) = P(odd) + P(divisor of 9) - P(odd and divisor of 9)
P(odd) = 4/8 = 1/2
P(divisor of 9) = 2/8 = 1/4
P(odd and divisor of 9) = 0 (there is no number that is both odd and a divisor of 9)
Substituting the values, we get:
P(odd or divisor of 9) = 1/2 + 1/4 - 0 = 3/4
To convert this into a percentage, we multiply by 100:
P(odd or divisor of 9) = 75%
Therefore, the probability of getting an odd number or a divisor of 9 when spinning the spinner once is 75%.
Learn more on probability here:
https://brainly.com/question/32117953
#SPJ11
Water flows into a tank at a rate of 15 litres per hour. How long will it take to fill a
tank that holds 750 litres?
Steps please, and quick
Answers
It will take 50 hours to fill the tank with 750 liters of water when water flows into a tank at a rate of 15 liters per hour
In the above question, It is given that,
Water flows in the tank at a rate of = 15 liters per hours
It means that, in a span of 1 hour the water flowing in the tank is 15 liters
We need to find,
How long will it take to fill a tank that holds 750 liters
To do that, our approach would be to first find the water flowing in the tank in 1 hour and we'll find time taken to fill water of 750 liters in the tank
Water flowing in the tank in 1 hour = 15 liters
Water flowing in the tank in x hour = 750/15 hours
= 50 hours
Hence, It will take 50 hours to fill the tank with 750 liters of water when water flows into a tank at a rate of 15 liters per hour
To learn more about, hours, here
https://brainly.com/question/13533620
#SPJ1
(a) Given a 3 x 3 matrix [A]= x 15 7
2 3 5
0 1 3
compute the value of x if [A] is not invertible.
(b) Determine the eigenvalues and its corresponding eigenvectors of matrix [A]
Answers
The eigenvalues and eigenvectors of [A] are:
λ1 = 5, v1 = [2, -3, 1]
λ2 = -1,
(a) The matrix [A] is invertible if its determinant is non-zero. Therefore, we can compute the determinant of [A] as follows:
det([A]) = x * (33 - 51) - 15 * (23 - 50) + 7 * (21 - 30)
= x * (-2) - 15 * 6 + 7 * 2
= -2x - 88
[Note: we used the formula for the determinant of a 3 x 3 matrix in terms of its elements.]
Since [A] is not invertible, its determinant must be zero. Therefore, we can set the determinant equal to zero and solve for x:
-2x - 88 = 0
x = -44
Therefore, x = -44 if [A] is not invertible.
(b) To find the eigenvalues and eigenvectors of [A], we need to solve the characteristic equation:
det([A] - λ[I]) = 0
where λ is the eigenvalue and I is the identity matrix of the same size as [A].
We have:
[A] - λ[I] = x-λ 15 7
2 x-λ 5
0 1 x-λ
Therefore, the characteristic equation is:
det([A] - λ[I]) = (x-λ) [(x-λ)(x-λ) - 51] - 15 [2*(x-λ) - 01] + 7 [21 - 5*0] = 0
Simplifying this equation, we get:
(x-λ)^3 - 5(x-λ) - 30 = 0
This is a cubic equation that can be solved using various methods, such as using the cubic formula or using numerical methods. The solutions to this equation are the eigenvalues of [A].
By solving the equation, we find the following three eigenvalues:
λ1 = 5
λ2 = -1
λ3 = 2
To find the eigenvectors corresponding to each eigenvalue, we need to solve the system of linear equations:
([A] - λ[I])v = 0
where v is the eigenvector corresponding to the eigenvalue λ. We can write this system of equations for each eigenvalue and solve for the corresponding eigenvector.
For λ1 = 5, we have:
[A]v = 5v
(x-5)v1 + 15v2 + 7v3 = 0
2v1 + (x-5)v2 + 5v3 = 0
v2 + 3v3 = 0
Using the last equation, we can choose v3 = 1 and v2 = -3. Substituting these values in the second equation, we get v1 = 2. Therefore, the eigenvector corresponding to λ1 = 5 is:
v1 = 2
v2 = -3
v3 = 1
Similarly, we can solve for the eigenvectors corresponding to λ2 = -1 and λ3 = 2. The final eigenvectors are:
For λ2 = -1:
v1 = 1
v2 = 0
v3 = -1
For λ3 = 2:
v1 = -1
v2 = 1
v3 = -1
Therefore, the eigenvalues and eigenvectors of [A] are:
λ1 = 5, v1 = [2, -3, 1]
λ2 = -1,
To learn more about eigenvalues visit:
https://brainly.com/question/31650198
#SPJ11
A rock climber averages 8 feet per minute. How many feet does the climber climb in 1 hour and 15 minutes?
Answers
1 hour and 15 minutes is 75 minutes
75*8 is 600 ft
Answer:
600 feet.
Step-by-step explanation:
1 hour and 15 minutes is equal to 75 minutes.
Therefore,
8 times 75 equals 600 feet.
What is the slope of a line perpendicular to the line y = -1/4x − 1?
Answers
Answer:
4
Step-by-step explanation:
The slope of a line that is perpendicular is the negative inverse of the original. The slope of the given line is -1/4. This means that the slope of the perpendicular line will be 4.
The slope of a line perpendicular to the line; y = -1/4x -1 is:. 4
The line y = -1/4x − 1 takes the slope-intercept form of a straight line; y = mx + c.
In essence, the slope of the line y = -1/4x − 1 is;
m1 = -1/4Also, the slope of two perpendicular lines are related as follows;
m1m2 = -1The slope of the line perpendicular to line y = -1/4x − 1 is therefore;
m2 = -1/(-1/4)m2 = 4.In essence, the slope of a line perpendicular to the line; y = -1/4x -1 is:. 4.
Read more:
https://brainly.com/question/2008693
Raashan, sylvia, and ted play the following game. each starts with $1. a bell rings every 15 seconds, at which time each of the players who currently have money simultaneously chooses one of the other two players independently and at random and gives $1 to that player. what is the probability that after the bell has rung 2019 times, each player will have $1? (a) 1 7 (b) 1 4 (c) 1 3 (d) 1 2 (e) 2
Answers
The probability that each player will have $1 after 2019 rings of the bell is: (c) 1/3.
To solve this problem, we need to think about the possible outcomes of the game. Each time the bell rings, each player has a 1/2 probability of giving $1 to one of the other two players. This means that after one ring of the bell, there are 2^3 = 8 possible outcomes, as each player can either give or not give money to each of the other players.
After two rings of the bell, there are 2^8 = 256 possible outcomes. After three rings, there are 2^12 = 4,096 possible outcomes. And so on.
To find the probability that after 2019 rings of the bell, each player will have $1, we need to find the total number of possible outcomes and the number of outcomes in which each player has $1.
The total number of possible outcomes after 2019 rings of the bell is 2^(3*2019) = 2^6057.
To count the number of outcomes in which each player has $1, we can use a combinatorial argument. We need to distribute 2019 dollars among the three players in such a way that each player ends up with exactly $1. This is equivalent to choosing two numbers between 0 and 2019, inclusive, and giving the first player the smaller amount, the second player the difference between the larger and smaller amounts, and the third player the remaining amount.
The number of ways to choose two numbers between 0 and 2019 is (2019+2) choose 2 = 2036 choose 2 = 2,066,530.
Therefore, the probability that each player will have $1 after 2019 rings of the bell is:
2,066,530 / 2^6057 = 1/3
So the answer is (c) 1/3.
In the game where Raashan, Sylvia, and Ted each start with $1 and a bell rings every 15 seconds, the probability that after the bell has rung 2019 times, each player will have $1 is (a) 1/7.
Learn more about probability at: brainly.com/question/30034780
#SPJ11.
Mr. Jones asks his students to generate the next two numbers in the sequence beginning –5.5, 11, ....
Taquan suggests that the sequence is geometric and the next two numbers are –22 and 44. Julia suggests that the sequence is arithmetic and the next two numbers are 27.5 and 44.
Which best explains which student is correct?
Taquan is correct. When the signs change in a sequence, the sequence is geometric. Each successive term is generated by multiplying by –2.
Julia is correct. When the numbers alternate between decimals and whole numbers, the sequence is arithmetic. Each successive term is generated by adding 16.5.
Both students could be correct about the types of possible sequences. However, one student made a computational error because it is not possible to arrive at a fourth term of 44 in two different ways.
Both students could be correct. Because two numbers are given in the original sequence, it is possible to find a common difference and common ratio between the successive terms.
Answers
A sequence can be an arithmetic sequence or geometric sequence or none.
The true statement is: (d) Both students could be correct. Because two numbers are given in the original sequence, it is possible to find a common difference and common ratio between the successive terms.
How to determine the student with the correct termsThe first two terms of the sequence are given as: -5.5, 11
Assume the sequence is an arithmetic sequence, the next two terms would be 27.5, 44.
This is gotten by adding 16.5 (the common difference) to the current terms
Assume the sequence is a geometric sequence, the next two terms would be -22, 44.
This is gotten by multiplying the current terms by 2 (the common ratio)
The above means that: Both students are correct
Read more about sequence at:
https://brainly.com/question/6561461
Answer:
D
Step-by-step explanation:
i took the test
If you are doing a linear regression, what is the slope of the line predicted by the null hypothesis?
Answers
The null hypothesis is that the linear regression model does not exist. This essentially means that the value of all the coefficients is equal to zero.
What is the null hypothesis?
The null hypothesis is a common statistical theory that contends that there is no statistical relationship or significance between any two sets of observed data and measured phenomena for any given single observed variable.
Here,
We have to find out the slope of the line predicted by the null hypothesis if we are doing a linear regression.
We concluded that the null hypothesis states that the slope is equal to zero, and the alternative hypothesis states that the slope is not equal to zero.
Hence, the null hypothesis is that the linear regression model does not exist. This essentially means that the value of all the coefficients is equal to zero.
To learn more about the null hypothesis from the given link
https://brainly.com/question/13135308
#SPJ4