Answers
Answer:
68°+47°+ x = 180°
115°+ x = 180°
115°-115°+x = 180°-115°
x = 65°
hope it's helpful ❤❤❤❤
THANK YOU.
Related Questions
Please help me I'm stuck. I will give 30 points for this one. Given triangle ABC tilde triangle PQR and your scale factor Complete the hotspots for these similar triangles and show work

Answers
The value for the hotspots of the similar triangles ∆ABC and ∆PWR are:
(1). angle B = 68°
(2). PQ = 5cm
(3). BC = 19.5cm
(4). area of ∆PQR = 30cm²
What are similar trianglesSimilar triangles are two triangles that have the same shape, but not necessarily the same size. This means that corresponding angles of the two triangles are equal, and corresponding sides are in proportion.
(1). angle B = 180 - (22 + 90) {sum of interior angles of a triangle}
angle B = 68°
Given that the triangle ∆ABC is similar to the triangle ∆PQR.
(2). PQ/7.5cm = 12cm/18cm
PQ = (12cm × 7.5cm)/18cm {cross multiplication}
PQ = 5cm
(3). 13cm/BC = 12cm/18cm
BC = (13cm × 18cm)/12cm {cross multiplication}
BC = 19.5cm
(4). area of ∆PQR = 1/2 × 12cm × 5cm
area of ∆PQR = 6cm × 5cm
area of ∆PQR = 30cm²
Therefore, the value for the hotspots of the similar triangles ∆ABC and ∆PWR are:
(1). angle B = 68°
(2). PQ = 5cm
(3). BC = 19.5cm
(4). area of ∆PQR = 30cm²
Read more about similar triangles here:https://brainly.com/question/14285697
#SPJ1
a technician must press a cable connector's retaining tab to remove a faulty fiber optic network cable. which of the following connectors does the cable use?
Answers
The cable connectors that requires pressing a retaining tab to remove the faulty fiber optic network cable is likely an SC (Subscriber Connector) connector.
The cable in question is likely using an SC (Subscriber Connector) connector. The SC connector is a commonly used fiber optic connector that features a push-pull mechanism with a retaining tab. To remove the faulty fiber optic network cable, the technician would need to press the retaining tab on the SC connector, which releases the connector from its mating receptacle.
The SC connector is known for its ease of use and high performance. It has a square-shaped connector body and utilizes a push-pull latching mechanism, which makes it convenient for installation and removal. By pressing the retaining tab, the technician can safely and efficiently disconnect the faulty fiber optic cable.
Learn more about fiber optic
brainly.com/question/31521334
#SPJ11
convert 123 into quinary number .
Answers
To convert decimal number 123 to quinary, follow these steps:
1. Divide 123 by 5 keeping notice of the quotient and the remainder.
2.Continue dividing the quotient by 5 until you get a quotient of zero.
3. Then just write out the remainders in the reverse order to get quinary equivalent of decimal number 123.

URGENT! PLEASE help me! Full solutions please, and no nonsense answers.

Answers
Answer:
\(\frac{1}{3x+52}\)
Step-by-step explanation:
Given
\(\frac{\frac{1}{x^2+51x+50} }{\frac{2}{x+50}+\frac{1}{x+1} }\)
= \(\frac{\frac{1}{(x+50)(x+1)} }{\frac{2(x+1)+x+50}{(x+50)(x+1)} }\)
= \(\frac{1}{(x+50)(x+1)}\) × \(\frac{(x+50)(x+1)}{2x+2+x+50}\) ← cancel (x + 50)(x + 1) on numerator/denominator
= \(\frac{1}{3x+52}\)
Answer:
\(\Large\boxed{\sf \bf \ \ \dfrac{1}{3x+52} \ \ }\)
Step-by-step explanation:
Hello, please consider the following.
We need to do something with that, right !?
\(\dfrac{\left(\dfrac{1}{x^2+51x+50\right)}}{\left(\dfrac{2}{x+50}+\dfrac{1}{x+1}\right)}\)
What can we say from \(x^2+51x+50\) ?
The sum of the zeroes is -51=(-1)+(-50) and the product is 50 = (-1) x (-50), so we can factorise. Let's do it !
\(x^2+51x+50=x^2+50x+x+50=x(x+1)+50(x+1)=(x+1)(x+50)\)
That's a pretty cool first result !
Now, let's play with the denominator.
\(\dfrac{2}{x+50}+\dfrac{1}{x+1}\\\\\text{*** We put on the same denominator which is (x+1)(x+50) ***}\\\\=\dfrac{2(x+1)}{(x+50)(x+1)}+\dfrac{x+50}{(x+1)(x+50)}\\\\=\dfrac{2(x+1)+x+50}{(x+50)(x+1)}\\\\=\dfrac{2x+2+x+50}{(x+50)(x+1)}\\\\=\dfrac{3x+52}{(x+50)(x+1)}\\\)
We are almost there.
Let's combine all these results together !
\(\dfrac{\left(\dfrac{1}{x^2+51x+50\right)}}{\left(\dfrac{2}{x+50}+\dfrac{1}{x+1}\right)}\\\\\\=\dfrac{\left(\dfrac{1}{(x+1)(x+50)\right)}}{\left(\dfrac{3x+52}{(x+50)(x+1)}\right)}}\\\\\\=\large\boxed{\dfrac{1}{3x+52}}\)
Hope this helps.
Do not hesitate if you need further explanation.
Thank you
Which of the following sets are subspaces of R3?
A. {(x,y,z) | x,y,z>0}
B. {(x,y,z) | 3x−6y+2z=−8}
C. {(x,y,z) | −5x+4y=0,−7x+8z=0}
D. {(x,x+5,x−4) | x arbitrary number }
E. {(8x−2y,−3x+9y,6x−9y) | x,y arbitrary numbers }
F. {(x,y,z) | 5x−4y+7z=0}
Answers
The subspaces are:B. {(x,y,z) | 3x−6y+2z=−8}C. {(x,y,z) | −5x+4y=0,−7x+8z=0}F. {(x,y,z) | 5x−4y+7z=0}Hence, the correct option is (B), (C), and (F).
A subspace is a subset of a vector space that satisfies the three axioms. Therefore, the given sets of R3 can be categorized as subspaces or not by using the three axioms of subspaces. Which of the following sets are subspaces of R3?A subspace has the following characteristics:It has the same dimension as the space. It contains the null vector. It is closed under vector addition. It is closed under scalar multiplication.Now, let's go through each option one by one.
A. {(x,y,z) | x,y,z>0}If we multiply any element of this set with a negative scalar, then we cannot obtain the same set. So it does not satisfy the third axiom. Therefore, it is not a subspace.
B. {(x,y,z) | 3x−6y+2z=−8}The set is a solution to a linear equation. It contains the null vector (0, 0, 0). The set is closed under vector addition and scalar multiplication. Therefore, it satisfies all three axioms of subspaces. So, it is a subspace.
C. {(x,y,z) | −5x+4y=0,−7x+8z=0}The set is a solution to a system of linear equations. It contains the null vector (0, 0, 0). The set is closed under vector addition and scalar multiplication. Therefore, it satisfies all three axioms of subspaces. So, it is a subspace.
D. {(x,x+5,x−4) | x arbitrary number}For any arbitrary value of x, we get a vector in this set. If we multiply any element of this set with a scalar, then we can obtain the same set. Therefore, it satisfies the third axiom of subspace. Also, it contains the null vector (0, 0, 0). But it does not satisfy the first axiom. So, it is not a subspace.
E. {(8x−2y,−3x+9y,6x−9y) | x,y arbitrary numbers}For any arbitrary values of x and y, we get a vector in this set. If we multiply any element of this set with a scalar, then we can obtain the same set. Therefore, it satisfies the third axiom of subspace. Also, it contains the null vector (0, 0, 0). But it does not satisfy the first axiom. So, it is not a subspace.
F. {(x,y,z) | 5x−4y+7z=0}The set is a solution to a linear equation. It contains the null vector (0, 0, 0). The set is closed under vector addition and scalar multiplication. Therefore, it satisfies all three axioms of subspaces. So, it is a subspace.The subspaces are:B. {(x,y,z) | 3x−6y+2z=−8}C. {(x,y,z) | −5x+4y=0,−7x+8z=0}F. {(x,y,z) | 5x−4y+7z=0}Hence, the correct option is (B), (C), and (F).
Learn more about subspaces subset
brainly.com/question/30459752
#SPJ11
Express the solution using interval notation
Answers
The solution to the inequality 5/w > 4/45, using interval notation, is given as follows:
(-∞, 56.25).
How to obtain the interval notation?The inequality for this problem is defined as follows:
5/w > 4/45.
Applying cross multiplication, we have that the solution can be obtained as follows:
4w < 45 x 5
w < 45 x 5/4
w < 56.25.
The solution is found similarly to an equality, isolating the desired variable, and finding the desired range of values.
The solution w < 56.25 is composed by values to the left of x = 56.25 on the number line, that is, values between negative infinity and 56.25, hence the interval is given as follows:
(-∞, 56.25).
Missing InformationThe problem is incomplete, hence it was adapted to show the solution to an inequality, and then written in interval notation.
More can be learned about inequalities at https://brainly.com/question/25275758
#SPJ1
Please help me with my work I’ll give Brainlest

Answers
Answer:
I believe it's a^2 * b^2 = c^2
Step-by-step explanation:
a^2 * 9^2 = 15^2
hope this helps! :)
What value must b have in the function f(x)=x^4+bx^2+1 so that the function has at least one inflection point over the interval (1,2)?
Answers
The function f(x) = x^4 + bx^2 + 1 has an inflection point at x = 0,
What is the inflection point?
An inflection point of a function is a point on the graph of the function where the concavity (curvature) of the graph changes. In other words, an inflection point is a point where the curve switches from being concave up to concave down, or vice versa.
The function f(x) = x^4 + bx^2 + 1 has an inflection point at x = 0, because the concavity of the graph changes at that point. To find the value of b such that the function has at least one inflection point over the interval (1,2), we can set x = 1 and x = 2 in the function and solve for b.
If we set x = 1, we get the equation f(1) = 1 + b + 1 = 0. Solving for b, we find that b = -2.
If we set x = 2, we get the equation f(2) = 16 + 2b + 1 = 0. Solving for b, we find that b = -9.
Since the function has an inflection point at x = 0 for any value of b, it will have at least one inflection point over the interval (1,2) for any value of b.
Therefore, the value of b can be any real number.
To learn more about Inflection point, Visit
brainly.com/question/10352137
#SPJ4
What’s the answer???

Answers
\(\sqrt{169}<\sqrt{184}<\sqrt{196}\\\\\sqrt{13^2}<\sqrt{184}<\sqrt{14^2}\\\\13<\sqrt{184}<14\\\\\text{Answer}:\text{C}\)
geometry, please help.

Answers
Answer:
MN ≈ 92.1
Step-by-step explanation:
given the figures are similar then the ratios of corresponding sides are in proportion, that is
\(\frac{MN}{IJ}\) = \(\frac{KL}{GH}\) ( substitute values )
\(\frac{MN}{21}\) = \(\frac{57}{13}\) ( cross- multiply )
13 MN = 21 × 57 = 1197 ( divide both sides by 13 )
MN ≈ 92.1 ( to the nearest tenth )
Which ists the steps in the correct order to fnd the medan of this data set? 24 16 23 30, 18 29 1 Put the numbers in order 2. Cross off highvlow pairs 3 Add the leftover numbers 4. Divsde the sum by 1 Pt the numbers in order 2. Cross of highlow pairs 1 Cross off hightow pars 2. Add the 3 Divsle the sum by over numbers 1 Cross of highlow pars
Answers
Answer:
1. Put the numbers in order.
2. Cross off high/low pairs.
3. Add the leftover numbers.
4. Divide the sum by 2.
Step-by-step explanation:
Given:
24, 16, 23, 30, 18, 29
The ordered steps involved in Calculating the median of the data set given :
1.) put the numbers in order: This involves arranging the numbers in the dataset usually in ascending order :
16, 18,23,24,29,30
2.) Cross off high/low pairs: take out equal amount of input from both the left and right hand side. Here we have (23, 34) left
3) Add the leftover numbers: Since the values left is more than one, both values are summed, we have (23+24) = 47
4.) Divide the sum by 2 : Get the average of the two numbers to obtain the median value. Here the average is (23+24)/2 = 47/2 = 23.5
Answer:
A: 1. Put the numbers in order.
2. Cross off high/low pairs.
3. Add the leftover numbers.
4. Divide the sum by 2.
Step-by-step explanation:
edg2020

some one plz help me

Answers
Df=sqr(10^2-8^2)
DF=6
SinE= opposite/hypotenuse
SinE=6/10=3/5
3. Given a nonempty polyhedron P={(x,y)∈Rn×Rk:Ax+By≥b}, let Q denote its projection onto x-space, i.e., Q={x∈Rn:∃y∈Rk,Ax+By≥b}. Prove or disprove the following statements by counterexamples: 1) Suppose that (x^,y^) is an extreme point of P. Is x^ an extreme point of Q ? 2) Suppose that x^ is an extreme point of Q. Does there exist a y^ such that (x^,y^) is an extreme point of P ? 3) Suppose that x^ is an extreme point of Q and P does not contain a line. Does there exist a y^ such that (x^,y^) is an extreme point of P ?
Answers
P does not contain a line, it means that for any x in R^n, there exists a unique y in R^k such that Ax + By ≥ b. Therefore, x^ is uniquely determined by y^, and (x^, y^) is an extreme point of P.
1) The statement is true. Suppose (x^,y^) is an extreme point of P. To show that x^ is an extreme point of Q, we need to prove that for any two distinct points x_1, x_2 in Q, the line segment connecting x_1 and x_2 lies entirely in Q. Since Q is the projection of P onto x-space, it means that for any x in Q, there exists y in R^k such that Ax + By ≥ b.
Now, let's assume x_1 and x_2 are two distinct points in Q. Since they belong to Q, there exist corresponding y_1 and y_2 in R^k such that Ax_1 + By_1 ≥ b and Ax_2 + By_2 ≥ b. Since P is a polyhedron, the set of points that satisfy Ax + By ≥ b is a convex set. Therefore, the line segment connecting x_1 and x_2, denoted by [x_1, x_2], lies entirely in P. Since the projection of a convex set onto a subspace is also a convex set, [x_1, x_2] lies entirely in Q. Thus, x^ is an extreme point of Q.
2) The statement is false. Suppose x^ is an extreme point of Q. It does not necessarily imply the existence of a corresponding y^ such that (x^, y^) is an extreme point of P. This is because the projection Q onto x-space may not capture all the extreme points of P. It is possible for multiple points in P to project to the same point in Q, making it impossible to uniquely determine y^.
3) The statement is true. If x^ is an extreme point of Q and P does not contain a line, then there exists a corresponding y^ such that (x^, y^) is an extreme point of P. Since P does not contain a line, it means that for any x in R^n, there exists a unique y in R^k such that Ax + By ≥ b. Therefore, x^ is uniquely determined by y^, and (x^, y^) is an extreme point of P.
Learn more about convex set
brainly.com/question/32604567
#SPJ11
man travels 60 miles to work at an average speed of 40mph. He travels home the same route at an average speed of 60mph. What is the average speed of his round trip
Answers
Answer:1881 6040mph 18x
can you solve the sums

Answers
\((a) {11}^{a} = 1331 \\ = > {11}^{a} = {11}^{3} \\ = > a = 3\)
\((b) {2}^{b} = \frac{1}{128} \\ = > {2}^{b} = (\frac{1}{2} ) ^{7} \\ = > {2}^{b} = {2}^{ - 7} \\ = > b = - 7\)
\((c) {9}^{c} = 243 \\ = > {3}^{2 \times c} = {3}^{5} \\ = > {3}^{2c} = {3}^{5} \\ = > 2c = 5 \\ = > c = \frac{5}{2} \\ = > c = 2.5\)
\((d) {10}^{d} = 0.01 \\ = > {10}^{d} = \frac{1}{100} \\ = > {10}^{d} =( \frac{1}{10} ) ^{2} \\ = > {10}^{d} = {10}^{ - 2} \\ = > d = - 2\)
Answers:a = 3b = -7c = 2.5d = -2Hope it helps.
Do comment if you have any query.
What is 24/240 as a decimal
Answers
Answer:
0.1
Step-by-step explanation:
Just take 24/24 which is 1 and move the decimal one place to the left because there is an extra 0 on the denominator
Find an equation of the tangent line to the graph of the function at the given point. y = 4x arccos(x − 1), (1, 2)
Answers

a family originally bought a home for $273,830. Now the home’s value is 30% higher than that. What is the value of the home now?
Answers
$355,394
100% +30% = 130% = 1.3
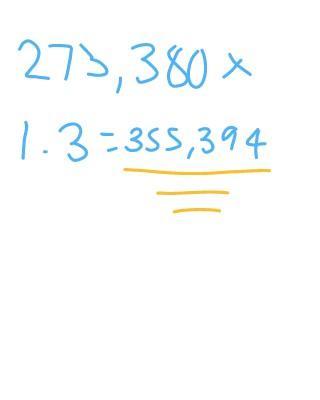
Answer:
So the home value is 30 percent higher then the original price.
So $273,830
It’s 30 percent higher.
I’m gonna do a short cut here but you can always find 30 percent of the number and add it back to the original value.
Well first 30 percent is 30/100 really since percent is out of a hundred.
We’re increasing 30 percent of the value.
The original value is already 100/100 since thats the full price and original.
We’re adding 30 percent of that so the new value is 130/100 or 130%
This would save a lot of steps and it’s a better way.
So find percentage like what we would do with any other equation.
Since here it’s 130% we multiply the value by 1.3.
Since 130/100 is 1.3 or you can always move the decimal to the left by 2 since it’s divided by a 100.
Now we multiply.
$273,830 * 1.3 = $355,979
Final answer is $355,979
what type of parent function is f (x) = 1/x
Answers
The function f(x) = 1/x represents the reciprocal function is a type of rational function.
The reciprocal function has the general form f(x) = 1/x, where x is any non-zero real number.
The reciprocal function is characterized by its graph, which is a hyperbola.
The graph of f(x) = 1/x consists of two branches that approach the x-axis and the y-axis as x approaches positive or negative infinity.
The parent function f(x) = 1/x has several key features:
As x approaches positive infinity, the function approaches zero.
This means that the graph gets closer and closer to the x-axis but never touches it.
As x approaches negative infinity, the function also approaches zero, but on the negative side of the x-axis.
The graph is symmetrical with respect to the line y = x.
This means that if you reflect one branch of the hyperbola over the line y = x, you will get the other branch.
The function is undefined at x = 0 since division by zero is not defined.
The reciprocal function and its variations have various applications in mathematics, physics and engineering, especially dealing with inverse relationships or situations where quantities approach zero or infinity.
For similar questions on function
https://brainly.com/question/11624077
#SPJ11
Please Help! 60 points for a rapid reply- please look at the question below= The Figure of circle A shown has a diameter of PR which intersects with QS at point B and the measurements shown, Calculate the following measures-


Answers
The measures in the circle given in the image above are calculated as:
1. m<PSQ = 130°; 2. m<AQS = 30°; 3. m(QR) = 100°; 4. m(PS) = 110°; 5. (RS) = 70°.
How to Find the Measures in the Circle?In order to find the measures in the circle shown, recall that according to the inscribed angle theorem, the measure of intercepted arc is equal to the central angle, but is twice the measure of the inscribed angle.
1. m<PSQ = m<PAQ
Substitute:
m<PSQ = 130°
2. Find m<PBQ:
m<PBQ = 1/2(m(PQ) + m(RS)) [based on the angles of intersecting chords theorem]
Substitute:
m<PBQ = 1/2(130 + 2(35))
m<PBQ = 100°
m<AQS = 180 - [m<BAQ + m<PBQ]
Substitute:
m<AQS = 180 - [(180 - 130) + 100]
m<AQS = 30°
3. m(QR) = m<QAR
Substitute:
m(QR) = 100°
4. m(PS) = 180 - m(RS)
Substitute:
m(PS) = 180 - 2(35)
m(PS) = 110°
5. m(RS) = 2(35)
m(RS) = 70°
Learn more about Measures in a Circle on:
https://brainly.com/question/27111486
#SPJ1
Drag numbers to complete the table for missing values of x
, x2
, and x3
.
Answers
The numbers to complete the table are
x x² x³
2 4 8
6 36 216
How to use the numbers to complete the tableFrom the question, we have the following parameters that can be used in our computation:
The incomplete table of values (see attachment)
On the first row, we have
x² = 4
Take the square root of 4
x = 2
Take the cube of 2
x³ = 8
On the second row, we have
x = 6
Take the square of 6
x² = 36
Take the cube of 6
x³ = 216
The above are the complete values of x, x² and x³
Read more about expression at
https://brainly.com/question/15775046
#SPJ1

Fatimah is x years old and nadia is 3 years older than fatmah. find expression, in it's simplest form in terms of x, for the sum of the girls ages in two years time and in y years time
Answers
The algebraic formula that represents the situation of the age difference between Fatimah and Nadia is x + 3 = y, where x, y > 0 and y > x.
How to derive an algebraic expression from a word problem
Herein we have a situation where two people have different ages, Fatimah has an age such that she is 3 years younger than Nadia. Let be x and y variables that respesent the ages of Fatimah and Nadia, respectively. In summary, the word problem can be reduced into the following algebraic expression:
y - x = 3 (Expression that represents age difference between Fatimah and Nadia)
x + 3 = y, where x, y > 0 and y > x. (1)
The algebraic formula that represents the situation of the age difference between Fatimah and Nadia is x + 3 = y, where x, y > 0 and y > x.
To learn more on word problems: https://brainly.com/question/15588055
#SPJ1
I NEED HELP ON THIS ASAP!!! IT'S DUE TONIGHT


Answers
Answer:
First Problem:
Transformation: Reflection across the x-axis, shift 2 units rightward
Equation: g(x)=-5^(x-2)
Second Problem:
Transformation: Reflection across the y-axis, shift 4 units upward
Equation: 10^-x+4
Step-by-step explanation:
Imagine folding a piece of paper and using the x or y axis as the crease marks. By folding them and comparing them, we can find out whether it is either the x-axis, y-axis, or both-axis. Then, we move the graph, to match the position in the second picture.
As for equations, exponential functions have the parent function of y=b^(x+c)+h. By plugging in any points given, let's say (1,5), we can see that 5=b^1 and simplifying shows 5=b. Therefore, the function is y=5^x. Using that first equation, we transform it. If over the x-axis, convert y=b^x to y=-b^x. If over the y-axis, convert y=b^x to y=b^-x. For horizontal shift, if going rightward, it is x-c. If going leftward, it is x+c. For vertical shift, if going up, b^x+h. If going down, b^x-h.
If unsure, plug-in points to see if your answer checks out with the equation :)
how do you find the zeros of a polynomial (step by step)
Answers
To find the zeros of a polynomial, set the polynomial equal to zero and solve for the variable.
How we find the zeros of a polynomial?To find the zeros of a polynomial, follow these step-by-step instructions:
Write the polynomial in standard form.Ensure that the polynomial is written in standard form, where the terms are arranged in descending order of degree.Set the polynomial equal to zero. Set the polynomial equal to zero by replacing the f(x) or P(x) with 0.Factor the polynomial (if possible). Try to factor the polynomial completely. Start by checking for any common factors among the terms and use techniques such as factoring by grouping or applying special factoring formulas.Apply the Zero Product Property. Once the polynomial is factored, set each factor equal to zero individually and solve for x. This step is based on the Zero Product Property, which states that if a product of factors is equal to zero, then at least one of the factors must be zero.Solve for x. Solve each equation obtained in the previous step to find the values of x that make each factor equal to zero. These values are the zeros of the polynomial.Verify and write the zeros. Check the obtained values of x by substituting them back into the original polynomial equation. If the result is zero, then the value of x is a zero of the polynomial. Write down all the zeros found.Learn more about Polynomial
brainly.com/question/11536910
#SPJ11
solve the following system of equations. if there is no solution, write dne in each coordinate of the ordered triplet. if there are an infinite number of solution, write each coordinate in terms of z . z. x 7
Answers
DNE in each coordinate of the ordered triplet are y is -7 , DNE ,y is-2.
Whais the explanation?1.) 2+3 = y + 12
Make y the formula's subject after adding the LHS.
5 = y + 12
Y = 5 - 12
Y = - 7
The answer to the equation is -7
2.) 2 + 13 = 1 +8
The equation cannot have a solution since there is no unknown variable and the sum of the numbers on the left hand side (LHS) does not equal the sum of the numbers on the right hand side (RHS).
3.) y - 7 = 2 - 11
RHS is added, and y is become the formula's subject.
Y - 7 = -9
Y = -9 + 7
Y = -2
The equation's answer is -2.
The complete question is:Solve the following system of equations. If there is no solution, write DNE in each coordinate of theordered triplet. If there are an infinite number of solution, write each coordinate in terms of z.2+3 = y + 12
2 + 13 = 1 +8
y - 7 = 2 - 11
To learn more about DNE refer to:
https://brainly.com/question/16938197
#SPJ4
If you want to scale your ratio up, you need to _________ .
Answers
If you want to scale your ratio up, you need to multiply or increase the values of both the numerator and the denominator of the ratio by the same factor.
A ratio represents the relationship between two quantities and is expressed as the quotient of two numbers. Scaling up a ratio means increasing the values of both the numerator and the denominator while maintaining the same relative relationship between them.
To scale up a ratio, you can follow these steps:
Determine the scaling factor: The scaling factor is the value by which you want to increase the ratio. It can be any positive number greater than 1.
Multiply both the numerator and the denominator by the scaling factor: Multiply the original numerator and denominator of the ratio by the scaling factor. This ensures that both quantities are scaled up proportionally.
By multiplying both parts of the ratio by the same scaling factor, you maintain the same ratio relationship while increasing the absolute values of the quantities.
For example, let's consider the ratio 2:5. If we want to scale it up by a factor of 3, we would multiply both the numerator and the denominator by 3:
2 * 3 : 5 * 3
6 : 15
The scaled-up ratio becomes 6:15, which maintains the same ratio relationship as 2:5 but with larger absolute values.
Scaling up a ratio can be useful in various scenarios, such as when you want to increase the size or quantity of something while maintaining the same relative proportions. It allows you to expand the scale of the ratio without altering the underlying relationship between the quantities involved.
In summary, to scale up a ratio, you need to multiply both the numerator and the denominator of the ratio by the same factor. This ensures that the ratio maintains its relationship while increasing the absolute values of the quantities.
Learn more about ratio at: brainly.com/question/13419413
#SPJ11
andace had scores of 96, 84, 95, and 82 on her first four exams of the semester. what score must she obtain on the fifth exam to have an average of 90 or better for the five exams
Answers
Andace needs to score at least 98 on her fifth exam to have an average of 90 or better for the five exams.
To find out what score Andace needs to get on the fifth exam, we can use the formula for the average (also known as the mean):
Average = (sum of all scores) / (number of scores)
We know that Andace needs an average of 90 or better for the five exams. Therefore, the sum of all five scores must be at least 450 (90 multiplied by 5).
The sum of Andace's first four scores is:
96 + 84 + 95 + 82 = 357
To get an average of 90 or better for the five exams, Andace needs to get a total of:
450 - 357 = 93
on her fifth exam.
Since she has already taken four exams and the maximum score she can get on her fifth exam is 100, we can subtract her first four scores from 93 to find out what she needs to score on her fifth exam:
93 - 96 - 84 - 95 - 82 = -164
Since it's not possible for Andace to score a negative number on her fifth exam, we can conclude that she needs to score at least 98 (93 - 5) to have an average of 90 or better for the five exams.
In conclusion, Andace needs to score at least 98 on her fifth exam to have an average of 90 or better for all five exams.
To know more about Average, refer here:
https://brainly.com/question/27646993#
#SPJ11
how would you find the surface area of a cube, if you knew the area of one face ???
Answers
Answer:
Step-by-stepAnswer:
just times the area by 6!
Step-by-step explanation:
if the surface area means area of all the faces of the cube, that means 6 areas of the same length and width! multiplying the area by 6 will result in your answer :)
There are 8 horses in race, how many ways can they finish first, second, and third?
Answers
Answer:
There are 336 ways to have 8 horses place for 1st, 2nd, and 3rd place
Step-by-step explanation:
p/5=30
what does p equal?
p=?
Answers
Answer:
150
Step-by-step explanation:
p/5=30
p=30*5
p=150
