Answers
Answer:
42.9
Step-by-step explanation:
81.9÷67.2=1.21875
1.21875*32=39
81.9-39=42.9
Related Questions
Which expression is equivalent to 3^-4*3^6
Answers
Answer:
3^2
Step-by-step explanation:
3^-4*3^6
3^-4+6
3^2
What is the equation of the line that passes through the point (-3, 1) and has a
slope of - 2
Answers
Step-by-step explanation:
slope = (y2-y1) / (x2-x1)
equation of the line y2 - y1 = m(x2-x1),
y2 = m(x2-x1) +y1
y2-y1 = -2(x2- (-3))
y2-y1 = -2x -6
y2 - 1 = -2x -6
y2 = -2x -5
Use the normal approximation to find the indicated probability. The sample size is n, the population proportion of successes is p, and X is the number of successes in the sample.
n = 93, p = 0.48: P(X ≤ 48)
Answers
The probability that X is less than or equal to 48 is approximately 0.023.
To use the normal approximation, we first need to check if the conditions are met:
1. The sample size is large enough: n*p = 93*0.48 = 44.64 and n*(1-p) = 93*0.52 = 48.36, both greater than 10.
2. The observations are independent: we assume that the sample is random and that the sample size is less than 10% of the population size.
Given these conditions, we can use the normal distribution to approximate the binomial distribution.
We standardize X using the formula:
z = \((X - n*p) / \sqrt{(n*p*(1-p)) }\)
Substituting the values, we get:
z = (48 - 93*0.48) / sqrt(93*0.48*0.52) = -1.99
Using a standard normal distribution table or calculator, we can find the probability:
P(X ≤ 48) ≈ P(z ≤ -1.99) = 0.023
Therefore, the probability that X is less than or equal to 48 is approximately 0.023.
Learn more about probability here:
https://brainly.com/question/30034780
#SPJ11
Help me please,I really need help lol

Answers
The interval notation for the solution to the given inequality is:
(6,∞).
What is the solution to the inequality?The inequality is solved similarly to an equality, applying the operations to isolate the variable.
For this problem, the inequality is given by:
3(3a - 6) > 12.
Dividing both sides by 3:
3a - 6 > 12.
Then:
3a > 18
a > 18/3
a > 6.
In interval notation, the solution is:
(6,∞).
More can be learned about inequalities at https://brainly.com/question/24372553
#SPJ1
Who got the answer to this ?

Answers
Answer:
B
Step-by-step explanation:
These two angles will be the same for the fact of A and B being parallel
Im not good at math at all but i need help so if anyone is super smart and can answer this before 11:59 that will help a-lot

Answers
4x^12
Steps:
Cancel out the common factor of 10
4x^14/x^2
=4x^12
Find the value of x
for which 3(2^x-^3)=384
PLEASE I NEED THE SOLUTIONS ITS URGENT
Answers
Answer is x=10
Step-by-step explanation:
Find a10 and an for the arithmetic sequence. a12=27,a14=38
Answers
The general term (an) of the arithmetic sequence is given by an = -94 + (n - 1) * 11. So, the 10th term (a10) is 5, and the general term (an) is -94 + (n - 1) * 11.
To find the 10th term (a10) and the general term (an) of an arithmetic sequence, we need to identify the common difference (d) between consecutive terms.
Given that a12 = 27 and a14 = 38, we can use these two terms to find the common difference.
We can calculate the common difference (d) by subtracting a12 from a14:
d = a14 - a12
= 38 - 27
= 11
Now that we have the common difference, we can find a10 by subtracting 2d from a12:
a10 = a12 - 2d
= 27 - 2(11)
= 27 - 22
= 5
Therefore, a10 = 5.
To find the general term (an), we can use the formula for an arithmetic sequence:
an = a1 + (n - 1)d
Since we know a12 and d, we can substitute these values into the formula:
27 = a1 + (12 - 1) * 11
27 = a1 + 11 * 11
27 = a1 + 121
Now we can solve for a1 by subtracting 121 from both sides:
a1 = 27 - 121
= -94
Therefore, the general term (an) of the arithmetic sequence is given by:
an = -94 + (n - 1) * 11
So, the 10th term (a10) is 5, and the general term (an) is -94 + (n - 1) * 11.
Learn more about arithmetic sequence here
https://brainly.com/question/6561461
#SPJ11
Find the unknown side of the triangle below.
9 in
18.8 in
15 in
8 in

Answers
If you do a^2+b^2=c^2 which basically means 8+x=17, x would add up with 8 to 17. So that’s why it’s 9 :)
Answer:
its actually 15 inches, cause if you bring the bottom line up and compare it to the 17 line its a smidge shorter so go with the largests number the less then 17. theres proof for the quiz itself
Step-by-step explanation:

Please help me answer

Answers
Answer:
Step-by-step explanation:
the circumference you make it using the diameter , pi times ( 3.142 times)
C = 13* 3.142 = 40.846
True or False. Exponential Functions will create a straight line on a graph
Answers
Answer:
False
Step-by-step explanation:linear functions will create a straight line on a graph, exponentials will not.
What is f(-6)? Hint: plug (-6) in for the variable p.
Complete the table.

Answers
Step-by-step explanation:
f(-7)= (-7)^2 + 6×(-7)=49-42= 7
f(-6)=36-36= 0
f(-5)=25-30= -5
f(-4)=16-24= -8
Plz help with this what is it. Multiply 2(5b)
Answers
Answer:
Step-by-step explanation:
As no identity applies on this, we use distributive property, the property is:
(
a
+
b
)
(
c
+
d
)
=
a
(
c
+
d
)
+
b
(
c
+
d
)
Using that
2
(
5
+
6
b
)
+
5
b
(
5
+
6
b
)
Expand the brackets
10
+
12
b
+
25
b
+
30
b
2
Solve
10
+
37
b
+
30
b
2
1) Inflation represents the rate of increase of the average
price of goods. If inflation decreases from 10% to 5%, does the
average price of goods decrease? Explain.
Answers
The average price of goods does not decrease but the rate at which the prices of goods increase has decreased.
Inflation represents the rate of increase of the average price of goods. If inflation decreases from 10% to 5%, the average price of goods does not decrease but the rate at which the prices of goods increase has decreased.
Inflation is the general increase in prices of goods and services in an economy over a period of time. It is expressed as a percentage increase in the average price of goods. If inflation is 10%, it means that on average, prices have increased by 10% over a certain period of time.
If inflation decreases from 10% to 5%, it means that the rate at which prices are increasing has decreased, but it does not mean that prices have decreased.For instance, if a basket of goods that cost $100 last year now costs $110 due to inflation, then a decrease in inflation rate from 10% to 5% means that the same basket of goods will cost $115 next year instead of $121.
Therefore, the average price of goods does not decrease but the rate at which the prices of goods increase has decreased.
Learn more about average here:
https://brainly.com/question/28341166
#SPJ11
NEED HELP WITH MATH GEOMETRY

Answers
The value of angle m∠FCG is 27.5.
x = 25
x = 35
We have,
1.
GCH and ECD are alternate angles.
This means,
GCH = 125 = ECD
And,
ECG and DCH are alternate angles.
This means,
ECG = DCH = x
Now,
GCH + ECD + ECG + DCH = 360
125 + 125 + x + x = 360
250 +2x = 360
2x = 360 - 250
2x = 110
x = 55
Now,
ECG = ECF + FCG
55 = ECF + FCG
ECF and FCG are equal.
So,
m∠FCG = 55/2 = 27.5
2.
The straight angles are formed by (5x + 20) and (2x - 5).
So,
5x + 10 + 2x - 5 = 180
7x + 5 = 180
7x = 180 - 5
7x = 175
x = 25
3.
2x + 43 and 2x - 3 are on the same side of the parallel lines.
So,
2x + 43 + 2x - 3 = 180
4x + 40 = 180
4x = 180 - 40
4x = 140
x = 35
Thus,
The value of angle m∠FCG is 27.5.
x = 25
x = 35
Learn more about corresponding angles here:
https://brainly.com/question/1597341
#SPJ1
please help I will give you ten points

Answers
Answer:
number 2 or 3
Step-by-step explanation:
How to do!!!
please help
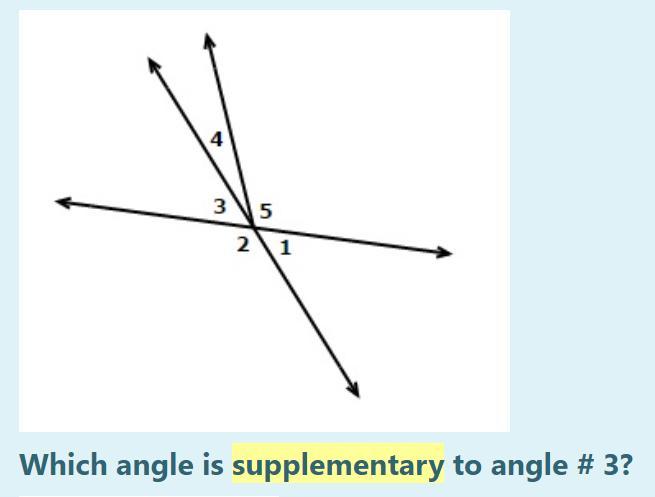
Answers
Step-by-step explanation:
Supplementary angle adds up yo 180°
So angle 2 is supplementary to angle 3
Supplementary angle adds up yo 180°
So angle 2 is supplementary to angle 3
2/3 as afraction with a denominator of 6
Answers
Answer:
4/6
Step-by-step explanation:
3 x 2 = 6
2 x 2 = 4
2/3 = 4/6
The number of ways of arranging all trials to be failures in a binomial distribution is:?
Answers
In a binomial distribution, the number of ways of arranging all trials to be failures is 1. This means that there is only one way to have all trials result in failures, as each trial can only have one possible outcome - a failure.
1. In a binomial distribution, each trial can result in either a success or a failure. Let's assume that there are n trials in total.
2. To arrange all trials to be failures, we need to ensure that no trial results in a success. Therefore, for each trial, there is only one possible outcome - a failure.
3. The number of ways of arranging all trials to be failures can be calculated using combinations. In this case, we need to select 0 successes from n trials. The number of ways to do this is given by the combination formula: C(n, 0) = 1, where C represents the combination.
Therefore, the number of ways of arranging all trials to be failures in a binomial distribution is given by the combination formula, C(n, k) = n! / (k! * (n-k)!).
To know more about binomial distribution visit:
https://brainly.com/question/29137961
#SPJ11
The number of ways of arranging all trials to be failures in a binomial distribution is always 1. This is because there is only one way to have no successes in a set of trials.
Regardless of the number of trials or the probability of success, the number of ways of arranging all trials to be failures in a binomial distribution is always 1.
The number of ways of arranging all trials to be failures in a binomial distribution can be determined using the formula for the binomial coefficient.
The binomial coefficient, often denoted as nCk or n choose k, represents the number of ways to choose k items from a set of n items, without considering their order. In the context of a binomial distribution, n represents the total number of trials and k represents the number of successes (in this case, 0).
To find the number of ways of arranging all trials to be failures, we can use the binomial coefficient formula:
nCk = n! / (k!(n-k)!)
In this case, since we want all trials to be failures, k is equal to 0. Thus, the formula simplifies to:
nC0 = n! / (0!(n-0)!) = n! / (0! * n!) = 1
For example, if we have 5 trials and we want all of them to be failures, there is only one possible arrangement: FFFFF, where F represents a failure.
Learn more about probability from the given link:
https://brainly.com/question/13604758
#SPJ11
Find the coordinates for the midpoint of with endpoints M(-3, 8) and 1(-7, 6)?
Answers
Answer:
The mid point coordinates are: (-5, 7)
Step-by-step explanation:
Please complete the awnser to this

Answers
for a list of five positive integers, none greater than 100, the mean is 1.5 times the mode. if 31, 58, 98, $x$ and $x$ are the five integers, what is the value of $x$?
Answers
The value of x from the given five integers is 34.
Here we have to find the value of x.
Data given:
Five positive number = 31, 58, 98, x, x
The mean is 1.5 times the mode.
Mean = (31 + 58 + 98 + x + x) / 5
= (187 + 2x) / 5
Mode = x
As the mean is 1.5 times the mode so from this we have:
mean = 1.5 × mode
(187 + 2x)/ 5 = 1.5x
187 + 2x = 7.5x
5.5x = 187
x = 34
Therefore the value of x is 34.
To know more about the mean, median and mode refer to the link given below:
https://brainly.com/question/14532771
#SPJ4
In ΔOPQ, o = 1.2 inches, p = 3.2 inches and ∠Q=37°. Find the area of ΔOPQ, to the nearest 10th of a square inch.
Answers
A patient consumed 1200 ml of liquid diet in the pass 20 hours. how many fluid oz. did he consume per hour?
Answers
The patient consumed approximately 2.03 fluid ounces per hour over the 20-hour period.
To calculate the fluid ounces consumed per hour, we need to convert the given milliliters to fluid ounces and then divide by the number of hours.
1 fluid ounce is equivalent to approximately 29.57 milliliters.
First, let's convert the 1200 milliliters to fluid ounces:
1200 ml / 29.57 ml/fl oz ≈ 40.59 fluid ounces
Now, let's calculate the fluid ounces consumed per hour:
40.59 fluid ounces / 20 hours ≈ 2.03 fluid ounces per hour
Therefore, the patient consumed approximately 2.03 fluid ounces per hour over the 20-hour period.
Learn more about ounces here
https://brainly.com/question/2853335
#SPJ11
Determine the largest integer value of x in the solution of the following
inequality.
3x-3<-16
Answers
Answer:
x<-13/3
Step-by-step explanation:
3x-3<-16
Add on both sides by 3
3x-3<-16
+3 +3
Simplify
3x<-13
Divide both sides by the same factor
3x<-13
÷3 ÷3
Cancel terms that are in both the numerator and denominator
x<-13/3
help !!!!
my math teacher wants me to answer this, and I have to give the answer in 10 minutes

Answers
Do 180-160 = 20 (Since 180 is a straight line)
The 115, x, and 20 form another straight line, so take 180-20-115. You get 45.
if we estimate that the mean recurrence interval of earthquakes in the 8.0-9.0 magnitude range in certain area is 1000 years, what is the probability of an earthquake in that magnitude range occurring in the next 30 years?
Answers
The probability of an earthquake in that magnitude range occurring in next 30 years is 3%.
The probability that the event will not occur for an exposure time of x years is:
\((1-\frac{1}{MRI} )^{x}\)
where, MRI = Mean Recurrence Interval = 1000
x = Years = 30
Therefore, Probability of not occurring = \((1-\frac{1}{1000} )^{30}\)
= \((\frac{999}{1000} )^{30}\)
= \((0.999)^{30}\)
= 0.97
Probability of occurring = 1 - 0.97
= 0.3
Probability percent = 0.03 * 100
= 3 %
Hence, probability is 3%.
To learn more about probability here:
https://brainly.com/question/11234923
#SPJ4
Find the circumference and area of the circle. Use 3.14 for π. Round to the nearest hundredth if necessary.
2 m
The circumference of the circle is about
m.
The area of the circle is about
m2.
Answers
Answer:
that's circumference is probably 11
Maya and Edward cut lawns in the summer to earn spending money. Maya has a newer lawnmower, so Edward takes 15 minutes longer to cut a lawn than Maya. Working together they can both cut a lawn in 18 minutes. How long would it take Edward to cut a lawn alone?
Answers
Answer:
The answer would be 45 minutes.
Step-by-step explanation:
Just skipped to the answer on Edementum.
A fraction is a way to describe a part of a whole. The time it takes Edward to cut the lawn alone is 45 minutes.
What is a Fraction?A fraction is a way to describe a part of a whole. such as the fraction ¼ can be described as 0.25.
Let the time taken by Maya to lawn the garden be x.
The rate at which Maya lawn = 1/x
Maya has a newer lawnmower, so Edward takes 15 minutes longer to cut a lawn than Maya. Therefore,
The rate at which Edward lawn = 1/(x+15)
Working together they can both cut a lawn in 18 minutes.
The rate at which they both work = 1/18
Now, the rate of working can be compared as,
1/x + 1/(x+15) = 1/18
(x+ x + 5)/x(x+15) = 1/18
(2x + 15)18 = x(x+15)
36x + 270=x² + 15x
x²-21x-270=0
x = 30, -9
Since time can not be negative. Therefore, the time it takes Edward to cut the lawn alone is,
x + 15
= 30 + 15
= 45 minutes
Hence, the time it takes Edward to cut the lawn alone is 45 minutes.
Learn more about Fraction:
https://brainly.com/question/1301963
#SPJ2
how much nitrogen and phosphorus should be included in the fertilizer for a farmer to get the highest yield? two levels of n (hi and low) are crossed with two levels of p (hi and low) giving four combinations of fertilizer to be studied: hh, hl, lh and ll. the experimenters had 12 acres available for the study and three acres were assigned at random to each of the combinations. assume the data are four independent srss, one from each of the four populations of planting densities, and that the distribution of the yields is normal. the data follow. treatment combination (np) yield (bushels per acre) n mean stdev hh 150.1, 113.0, 118.4 3 127.17 20.04 hl 166.9, 120.7, 135.2 3 140.93 23.63 lh 165.3, 130.1, 139.6 3 145.00 18.21 ll 134.7, 138.4, 156.1 3 143.07 11.44 answer the following questions: 1. the farmers are interested in whether there is any difference between the low-low combination (it is the cheapest) and the average of the remaining three levels. what hypotheses do they want to test? 2. what contrast would be used to test this hypothesis? 3. what contrast would be used to compare the high- to low-nitrogen content fertilizers? 4. what about for the high- to low-phosphorus content fertilizers? 5. what contrast compares the ll combination to the hh combination? 6. for each of the contrasts above, list the contrast coefficients.
Answers
The contrast coefficients would be as follows:
µll - (µhh + µhl + µlh) / 3: -1, -1, -1, 3µhl - µll: 1, -1, 0, 0µlh - µhl: 0, 1, -1, 0µll - µhh: -1, 0, 0, 1The farmers are interested in whether there is any difference between the low-low combination (it is the cheapest) and the average of the remaining three levels. The hypotheses they want to test are:
H0: µll - (µhh + µhl + µlh) / 3 = 0HA: µll - (µhh + µhl + µlh) / 3 ≠ 0
To test this hypothesis, the following contrast would be used:
µll - (µhh + µhl + µlh) / 3To compare the high- to low-nitrogen content fertilizers, the following contrast would be used:
µhl - µllTo compare the high- to low-phosphorus content fertilizers, the following contrast would be used:
µlh - µhlTo compare the ll combination to the hh combination, the following contrast would be used:
µll - µhhFor each of the contrasts above, the contrast coefficients would be as follows:
µll - (µhh + µhl + µlh) / 3: -1, -1, -1, 3µhl - µll: 1, -1, 0, 0µlh - µhl: 0, 1, -1, 0µll - µhh: -1, 0, 0, 1Learn more about coefficients
brainly.com/question/22241464
#SPJ11
