What is the standard deviation of this data? Round your answer to the nearest hundredth of a number?
10, 12, 8, 2
Answers
Answer:
3.74
Step-by-step explanation:
Count, N: 4
Sum, Σx: 32
Mean, μ: 8
Variance, σ2: 14
Hope this helped!
Related Questions
farm b has a 200 ft well that uses 10000 cubic feet of natural gas per year. if the cost of natural gas is the same a farm a, what is the annual cost to operate this well
Answers
Annual cost to operate farm B well with cost of natural gas $2.50 per 1,000 cubic feet and uses of 10000cubic feet of natural gas per year is $25.
As given,
Farm A:
Cost of natural gas per 1,000 cubic feet=$2.50
Farm B:
Uses of natural gas per year = 10000cubic feet
Cost of natural gas of farm B is same as farm A
Cost of natural gas per 1,000 cubic feet=$2.50
⇒1cubic feet=2.50/1000
Annual cost to operate 200ft well that uses 10000 cubic feet natural gas
10000 cubic feet=(2.50 ×10000)/1000
=$25
Therefore, annual cost to operate farm B well with cost of natural gas $2.50 per 1,000 cubic feet and uses of 10000cubic feet of natural gas per year is $25.
The complete question is:
Farm A has a 100 ft well that uses 7,000 cubic feet of natural gas per year. If the cost of natural gas for farm A is $2.50 per 1,000 cubic feet. And farm B has a 200 ft well that uses 10000 cubic feet of natural gas per year. if the cost of natural gas is the same a farm A, what is the annual cost to operate this well?
Learn more about annual cost here
brainly.com/question/14431362
#SPJ1
GUYS I NEED HELP WITH THIS ASAP!! PLS PLS PLS PLSSSSSS tysm to anyone who helps me. Luv y'all

Answers
27/90 (27 is the number of copper coins)
reduce it to give you 3/10
Can someone give me the answer quickly

Answers
Answer:
I think the answer is 42%
I don't really know for sure though
evaluate the expression under the given conditions. tan(2); cos() = 7 25 , in quadrant i
Answers
The required answer is the value of tan(2) is approximately -2352/3669.
To evaluate the expression under the given conditions, we will first determine the value of sin() using the Pythagorean identity and then use the double-angle formula for tan(2).
A Quadrant is circular sector of equal one quarter of a circle ,or a half semicircle. A sector of two-dimensional cartesian coordinate system. The Pythagorean identity, are useful expression involving the function need to simplified.
Given: cos() = 7/25, and is in Quadrant I.
Step 1: Find sin()
Since we are in Quadrant I, sin() is positive. Using the Pythagorean identity, sin^2() + cos^2() = 1, we can find sin().
sin^2() + (7/25)^2 = 1
sin^2() = 1 - (49/625)
sin^2() = (576/625)
sin() = √(576/625) = 24/25
we are called the Pythagorean identity is Pythagorean trigonometric identity, is expression A to B .
The same value for all variables within certain range. Angle is double or multiply by 2 so we called double- angle.
Step 2: Find tan(2) using the double-angle formula
The double-angle formula for tangent is: tan(2) = (2 * tan()) / (1 - tan^2())
First, we find tan():
tan() = sin() / cos() = (24/25) / (7/25) = 24/7
Now, use the formula for tan(2):
tan(2) = (2 * (24/7)) / (1 - (24/7)^2)
tan(2) = (48/7) / (1 - 576/49)
tan(2) = (48/7) / ((49 - 576) / 49)
tan(2) = (48/7) * (49 / (-527))
tan(2) = (-2352 / 3669)
So, under the given conditions, the value of tan(2) is approximately -2352/3669.
To know more about the Pythagorean identity. Click on the link.
https://brainly.com/question/29003523
#SPJ11
PLEASE HELP! ;-;
A particle rotates in a clockwise motion according to the equation x=3cos(0.2t+0.813) what is its frequency?
Answer= [ ? ] hertz
Answers
The particle has a frequency of 0.032 hertz.
The particle experiments a sinusoidal motion, whose mathematical model is described below:
\(x = x_{o} + A\cdot \cos (\omega\cdot t + \phi)\) (1)
Where:
\(x\) - Current position, in meters.\(x_{o}\) - Initial position, in meters. \(\omega\) - Angular frequency, in radians per second. \(t\) - Time, in seconds.\(\phi\) - Angle phase, in radians.The frequency (\(f\)), in hertz is defined by this formula:
\(f = \frac{\omega}{2\pi}\) (2)
By direct observation on the formula described in statement we find that \(\omega = 0.2\,\frac{rad}{s}\), then we find the frequency of the particle by (2):
\(f \approx 0.032\,hz\)
The particle has a frequency of 0.032 hertz.
We kindly invite to check this question on simple harmonic motion: https://brainly.com/question/17315536
...................................................

Answers
Answer:
11.21157846 =x
Step-by-step explanation:
We know log b (a) = c can be written as b^c =a
log 3 (x) = 2.2
3^2.2 = x
11.21157846 =x
Answer:
\(\large \boxed{\sf \bold{A.} \ x=11.21}\)
Step-by-step explanation:
\(\large \sf log_3 (x)=2.2\)
Solve this by converting the logarithmic statement into its equivalent exponential form, using the relationship:
\(\large \sf log_b(y)=x\)
\(\large{\sf y=b^x}\)
Apply the relationship.
\(\large \sf log_3 (x)=2.2\)
\(\large \sf x=3^{2.2}\)
\(\large \sf x=11.21157845...\)
\(\large \sf x \approx 11.21\)
Which multiplication problem us modeled on the number line?
2(-4)
4(2)
2(4)
4(-2)

Answers
Answer:
2(-4)
Immediately, we can narrow it down to the first and last answer choices, since the product is negative. Since there are 4 arrows going left on the number line, the answer to this problem is 2(-4).
What is the slope-intercept form of the line represented in the table shown?
X Y
-2 14
-1 12
0 10
1 8
2 6
3 4
Step 1: Find the y-intercept:
Step 2: Choose any two points from the table to find the slope:
Step 3: Use the newly-found slope to write the slope-intercept equation. The form
for that is y = mx + b.
Step 4: Check your work. Choose an ordered pair from the table and substitute
into the newly-found equation
Answers
Answer: The slope-intercept form is y = -2x + 10
Step-by-step explanation:
Step 1: The y-intercept is the point where x=0, so that is (0,10)
Step 2: Use the points (-2,14) and (-1,12) to find the slope
Slope (m) = ΔY/ΔX = -2/1 = -2
Step 3: The slope-intercept form is:
y = mx+b
y = (step 2 value) x + (step 1 value)
y = -2x+10
Please remember to vote this as Brainliest if I earned it!
Please help anybody good at Geometry?

Answers
Answer
<CFE
Step-by-step explanation:
alternate means across Interior between the lines

If there is no joint variability between two variables, then the r value will be?
Answers
Answer:
If r=0, there is absolutely no relationship between the two variables.
Step-by-step explanation:
What is the value of x in the triangle?

Answers
Answer: C
Using 45-45-90 triangle theorem
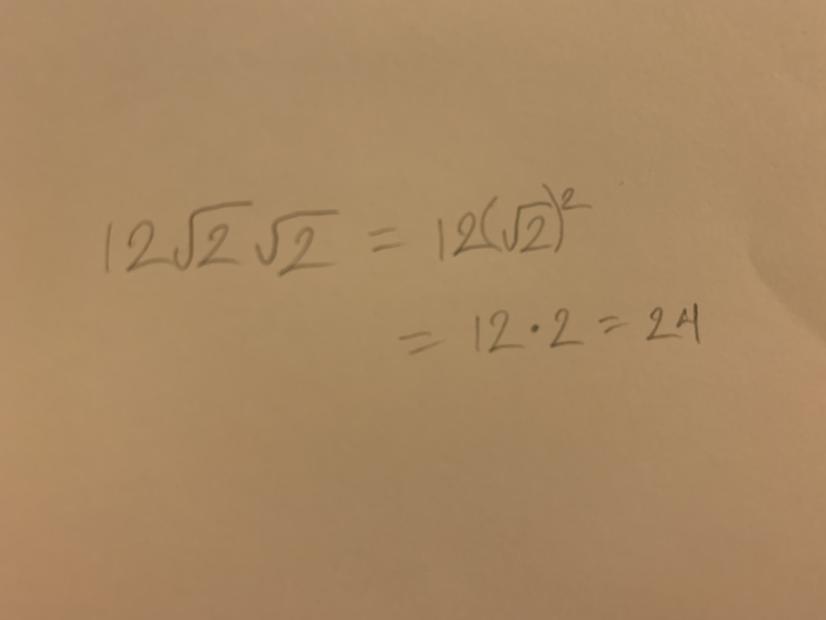
89
44
What is the value of v?
V=
o
Answers
Step-by-step explanation:
djzbiznJzlzbzjdkzlz?kskdbdid jaozbizz,#
Yuto left his house at 10 a.m. to go for a bike ride. By the time Yuto’s sister Riko left their house, Yuto was already 5.25 miles along the path they both took. If Yuto’s average speed was 0.25 miles per minute and Riko’s average speed was 0.35 miles per minute, over what time period in minutes, t, starting from when Riko left the house, will Riko be behind her brother? Riko will be behind Yuto when 0 ≤ t < minutes.
Answers
Answer: 52.5 minutes
Step-by-step explanation:
Answer:
The person below me is right
it's 52.5
Step-by-step explanation:
4x + 6y = -22
y + 3x = 1
Solution
Answers
Answer:
(-7,22)
Step-by-step explanation:
X=-7 and y=22
Which of the following are valid names for the given triangle? Check all that apply.

Answers
Answer:
a, b, e,f
Step-by-step explanation:
i dont have one
10 POINTS
please help me!!

Answers
why: when conducting a survey to determine approximations in a population, it’s best to eliminate any and all biases for best results. Households who live near a park or have their own front yards will skew results as the rest of the population may not have access to those things, thus are more likely to not have a dog.
b) 8/20= 0.40
600*0.40= 240
What is the surface area of the cylinder with height 8 mi and radius 5 mi? Round your
answer to the nearest thousandth.
Answers

below are the weights, in pounds for samples of offensive and defensive linemen in the national football league. offense: 335 301 307 252 260 307 325 310 305 305 264 325 defense: 284 290 286 355 305 295 297 325 310 297 314 348 compute the best measure of center for the defensive linemen and describe why you choose that measure of center. compute the best measure of spread for the defensive linemen and describe why you choose that measure of spread. compute the standard deviation for the offense: compute the standard deviation for the defense: write a sentence or two describing the information that would give you if you were purchasing uniforms for each group (offensive and defensive linemen).
Answers
Best measure of center for defensive linemen is the sample mean as it is not heavily influenced by outliers. Best measure of spread for defensive linemen is the sample standard deviation as it provides a measure of how spread out the data is from the mean.
Standard deviation for the offense is 26.16 and for the defense is 23.03. These values indicate that the weights of the offensive linemen are more spread out than the weights of the defensive linemen.
If you were purchasing uniforms for each group, this information would be useful in determining the range of sizes needed for each group and ensuring that there are enough uniforms available in each size. It would also be helpful in determining if any custom sizing needs to be done for certain players. Additionally, this information could be used to inform decisions regarding player nutrition and conditioning programs, as it may be desirable for certain players to gain or lose weight in order to perform optimally on the field.
To learn more about standard deviation, click here: brainly.com/question/475676
#SPJ11
the number of hours spent per week on household chores by all adults has a mean of 26.3 hours and a standard deviation of 7.4 hours. the probability, rounded to four decimal places, that the mean number of hours spent per week on household chores by a sample of 46 adults will be more than 26.75 is:
Answers
This question is about probability. The answer for this question is 34,09%.
Step-by-step explanation:
Suppose there was survey that state that the number of hours spent per week on house hold course of adult has mean 26,3 and standard deviatiador 7,4 and, sample are 46.
First, we need to know the base formula for probability given a mean and standard deviation.
First we need to know the z-score with this formula:
z-score =( x -μ )/ δ
Where:
X = individual data
μ = population mean
δ = population standard deviation.
But in this case, we were asked about the probabilty mean of 46 people. Then, we can use this formula :
Z-score =(x- μ) / (δ /√n)
Where :
X = sample mean
μ = population mean
δ = population standard deviation
Then we can find the z-score in z-table value.
Given :
X = 26,75
μ = 26,3
δ = 7,4
n = 46
Question :
Probability mean more than 26,75
Answer :
Z-score = (x- μ) / (δ /√n)
Z-score = (26,75 - 26,3)/ (7,4/√46)
Z-score = (0,45)/ (1,09)
Z-score = 0,4128
if we look in z-score table, we get number 0,6591.The probability that the mean hours spent per week on household chores by a sample of 46 adults will be more than 26.75 is 1 substract by the value of z-score ,
So, the probability mean for working adult more than 26,75 is 1 - 0,6591 = 0,3409 = 34,09%
Learn more about probabilty here :
brainly.com/question/15352354
#SPJ4
Solve.
13) Peter borrows $5000 at a rate of 9% compounded monthly. Find how much Peter owes at the end of 3 years.
Use: A=P(1+r/n)^nt
Round to two decimal places.
Answers
The final amount is higher than the principal amount because of the effect of Compounding interest. The interest is calculated monthly and added to the principal, resulting in a higher amount at the end of the term.
We are given:
Principal amount (P) = $5000
Rate of interest (r) = 9% per annum
Compounding frequency (n) = 12 (monthly)
Time period (t) = 3 years
Using the formula for compound interest:
A = P(1 + r/n)^(nt)
Substituting the given values, we get:
A = $5000(1 + 0.09/12)^(12*3)
A = $5000(1.0075)^36
A = $6817.60
Therefore, Peter owes $6817.60 at the end of 3 years.
the final amount is higher than the principal amount because of the effect of compounding interest. The interest is calculated monthly and added to the principal, resulting in a higher amount at the end of the term.
To know more about Compounding interest.
https://brainly.com/question/24274034
#SPJ11
A corporation has a continuous compounded bank account with 2.7% annual interest. The board of directors has placed $95218 in the account, making the formula for the amount in the account after t years F(t) = 9521800276. At what rate is the account growing after 6 years? Round your answer to two decimal places.
Answers
The formula for the amount in the account after t years is given by:
F(t) = 9521 *\(e^(0.027t)\)
Let's find out:
We want to find the rate at which the account is growing after 6 years, which is the first derivative of the function F(t) with respect to t, evaluated at t = 6:
F'(6) = (d/dt) [9521 * \(e^(0.027t)\)] | t=6
Using the chain rule of differentiation, we get:
F'(6) = 9521 * 0.027 * \(e^(0.027t)\) | t=6
F'(6) = 9521 * 0.027 *\(e^(0.027*6)\)
F'(6) ≈ 1429.97
Rounding to two decimal places, the rate at which the account is growing after 6 years is approximately 1429.97. The units of the rate are dollars per year.
To know more about derivatives visit
brainly.com/question/30365299
#SPJ1
\(\frac{6}{0}\)
Answers
Answer:
Not Defined
Step-by-step explanation:
Anything divided by 0 is said to be infinity or not defined.
10 points
Multiply (3.5x10^-6)x(2x10^-4) *
Answers
Answer:
Step-by-step explanation:
Multiply 3.5 and 2 together, obtaining 7.
Then add the exponents -6 and -4, obtaining -10.
The product is thus 7·10^(-10), or, after simplification,
7·10^(-9), or
7
----------
10^9
you intend to conduct a test of homogeneity for a contingency table with 8 categories in the column variable and 2 categories in the row variable. you collect data from 447 subjects. what are the degrees of freedom for the distribution for this test?
Answers
The degree of freedom for the distribution in this test of homogeneity is 7.
For the degrees of freedom for the test of homogeneity for a contingency table, we use the formula:
df = (number of rows - 1) × (number of columns - 1)
In this case, the contingency table has 2 categories in the row variable and 8 categories in the column variable. Therefore, the number of rows is 2, and the number of columns is 8.
Substituting these values into the formula, we get
df = (2 - 1) × (8 - 1)
df = 1 × 7
df = 7
Therefore, the degree of freedom for the distribution in this test of homogeneity is 7.
To know more about degrees of freedom click here :
https://brainly.com/question/31540339
#SPJ4
If you are paid a salary of $48,240 annually, how much would you expect to make per
month?
0.13
Answers
Answer:
B
Step-by-step explanation:
Answer:
$4.20 Per month = $4.2/1month
Step-by-step explanation:
1 year = 12 months
Proportions:
12 months ⇒ $48.24
1 month ⇒ $P
P = 48.24*1/12
P = $4.2
7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17 and 18 Use Part 1 of the Fundamental Theorem of Calculus to find the derivative of the function. 7 g(x) = { vt ++3 dt Jo Answer 8. g(x) = {* In (1+tº) dt
Answers
By using Fundamental Theorem of Calculus, we find the derivative of the function g(x) = In { sqrt( t + t^3)dt } limit from x to 0 is ln(sqrt(x + x^3)). The derivative of the function g(x) = { In (1+t^2) dt} where limit are from x to 1 is ln(1 + x^2).
The Fundamental Theorem of Calculus, which states that if a function is defined as the definite integral of another function, then its derivative is equal to the integrand evaluated at the upper limit of integration.
So, applying this theorem, we have:
g'(x) = d/dx [∫x_0 ln(sqrt(t + t^3)) dt]
= ln(sqrt(x + x^3)) * d/dx (x) - ln(sqrt(0 + 0^3)) * d/dx (0)
= ln(sqrt(x + x^3))
Therefore, g'(x) = ln(sqrt(x + x^3)).
Using the Fundamental Theorem of Calculus, we have:
g'(x) = d/dx [∫1_x ln(1 + t^2) dt]
= ln(1 + x^2) * d/dx (x) - ln(1 + 1^2) * d/dx (1)
= ln(1 + x^2)
Therefore, g'(x) = ln(1 + x^2).
To know more about Fundamental Theorem of Calculus:
https://brainly.com/question/30761130
#SPJ4
____The given question is incomplete, the complete question is given below:
Use Part 1 of the Fundamental Theorem of Calculus to find the derivative of the function. 7 g(x) = In { sqrt( t + t^3)dt } limit from x to 0. 8. g(x) = { In (1+t^2) dt} where limit are from x to 1.
May someone please help me with this question

Answers
Answer:
2+i or 2-i (D)
Step-by-step explanation:
First you use the quadratic formula. X= (-b +/- \(\sqrt{b^{2}-4ac }\))/2a
a=1
b=-4
c=5
X= (4 +/- \(\sqrt{16-20}\))/2
X=(4 +/- \(\sqrt{-4}\))/2
The square root of -4 is 2i. i=√-1. Therefore 2i= 2√-1 .If you simplify that, it becomes √-4i.
X= (4+/- 2i)/2
X= 2+/-i
X= 2+i or 2-i
If the value of a is 8 in f(x)=ax^2 what does the graph look like?
A) a parabola that opens down
B) a parabola that opens up
C) a parabola that opens left
D) a parabola that opens right
Answers
Answer:
B
Step-by-step explanation:
Graphs with x^2 look like a U shape as the negative x values will still result in a positive y value since a negative squared is a positive.
can someone pls help me? thank u

Answers
Please mark me as brainliest
Answer:
answer is. option (b) answer
Find the sum of the 25th term of an AP 3,10,17
Answers
The sum of the 25th term of the AP 3, 10, 17 is 171.
The sum of the 25th term of an arithmetic progression (AP) 3, 10, 17 can be found using the formula for the nth term of an arithmetic progression, which is:
aₙ = a₁ + (n - 1) d
where aₙ is the nth term, a₁ is the first term, d is the common difference, and n is the number of terms.
In this case, a₁ = 3, d = 10 - 3 = 7, and n = 25. Plugging in these values into the formula, we get:
a₂₅ = 3 + (25 - 1) 7
a₂₅ = 3 + 168
a₂₅ = 171
Therefore, the sum of the 25th term of the AP 3, 10, 17 is 171.
Learn more about arithmetic progression here: https://brainly.com/question/18828482.
#SPJ11