What is the square root of 24 to the 16th power
Answers
Answer:
24 ^ 8
Step-by-step explanation:
sqrt(24) ^ 16th power
Rewriting the square root as ^ 1/2
24 ^ 1/2 ^ 16
We know that a^b^c = a^ (b*c)
24 ^ (1/2*16)
24 ^ 8
Answer:
2²⁴ *3⁸ or 24⁸
Step-by-step explanation:
the square root of 24 to the 16th power can be written as 24
(\(\sqrt{24}\) )¹⁶
√ means power of 1/2 so (\(\sqrt{24}\) )¹⁶ = (24)^(¹⁶/₂) = 24⁸ or
24 = 4*6 and \(\sqrt{24} = 2\sqrt{6}\)
then (2\(\sqrt{6}\) )¹⁶= 2¹⁶ *6⁸ = 2¹⁶ * 2⁸ *3⁸ = 2²⁴ *3⁸
Related Questions
Tekan-Tekan Sdn. Bhd. has order for 200 Model AS-120 calculator for delivery on day 200. The calculator consists of three parts. Components 2 and 3 form subassembly 1 . Sub-assembly 1 and component 4 form the final assembly. Following are the work centers and times of each operation. Table Q3(a) shows routine file of the operation. Assuming: - Only one machine is assigned to each operation - The factory works on 8-hour shift, 5 days a week - All parts move in one lot of 200. (a) Illustrate the backward schedule based on the information given above. (12 marks) (b) Identify when component 3 must be started to meet the delivery date. (2 marks)
Answers
Component 3 must be started on day 197 to meet the delivery date of day 200.
To illustrate the backward schedule, we need to start from the delivery date (day 200) and work our way backward, taking into account the lead times and dependencies of each operation.
(a) Backward schedule:
Operation | Work Center | Time (hours) | Start Day
--------------------------------------------------------
Final Assembly | Work Center 1 | 1 | 200
Sub-assembly 1 | Work Center 2 | 2 | 199
Component 4 | Work Center 3 | 3 | 197
Component 2 | Work Center 4 | 4 | 196
Component 3 | Work Center 5 | 3 | ????
(b) To identify when component 3 must be started to meet the delivery date, we need to consider its dependencies and lead times.
From the backward schedule, we see that component 3 is required for sub-assembly 1, which is scheduled to start on day 199. The time required for sub-assembly 1 is 2 hours, which means it should be completed by the end of day 199.
Since component 3 is needed for sub-assembly 1, we can conclude that component 3 must be started at least 2 hours before the start of sub-assembly 1. Therefore, component 3 should be started on day 199 - 2 = 197 to ensure it is completed and ready for sub-assembly 1.
Hence, component 3 must be started on day 197 to meet the delivery date of day 200.
Learn more about Scheduling here:
brainly.com/question/30012511
#SPJ4
PLS HELP ASAP THANKS ILL GIVE BRAINLKEST PLS IM BEGGUNG YOU

Answers
First Question is boolean,
Question 35 is probably floating point ,
Question 36 is probably an integer, since it shows 1, 2, 3, and 1, 2, 3 are not fractions, and integers are whole numbers.
Im not 100% sure but I hope I helped,
Have a nice day/night :)
find the number c that satisfies the conclusion of the mean value theorem for the function f(x) = 3 ln x on the interval [1, e2 ]
Answers
The value of c that satisfies the conclusion of the Mean Value Theorem (MVT) for the function f(x) = 3 ln x on the interval [1, e²] is c = 2(e² - 1) / 3.
According to the Mean Value Theorem (MVT), if a function f is continuous on the interval [a, b] and differentiable on the open interval (a, b), then there exists at least one number c in the open interval (a, b) such that
f'(c) = [f(b) - f(a)] / (b - a)
The first step is to evaluate f(a) and f(b) for the given function f(x) = 3 ln x on the interval [1, e²].f(a) = f(1)
= 3 ln 1
= 0f(b)
= f(e²)
= 3 ln e²
= 6
Now we differentiate the function f(x) = 3 ln x to find f'(x)f(x) = 3 ln xf'(x) = (3/x)
The Mean Value Theorem (MVT) states that there exists a number c in the interval (a, b) such that
f'(c) = [f(b) - f(a)] / (b - a)
We have found the values of f(a), f(b), and f'(x) which are:f(a) = 0f(b) = 6f'(x) = (3/x)
Since the interval is [1, e²], we have
a = 1b = e²
Now, we can substitute these values in the Mean Value Theorem (MVT)
f'(c) = [f(b) - f(a)] / (b - a)(3/c) = [6 - 0] / (e² - 1) (Simplifying)
f'(c) = 3c = 2(e² - 1) (Multiplying both sides by e² - 1)c = 2(e² - 1) / 3
The value of c that satisfies the conclusion of the Mean Value Theorem (MVT) for the function f(x) = 3 ln x on the interval [1, e²] is c = 2(e² - 1) / 3.
Know more about the Mean Value Theorem (MVT) here:
https://brainly.com/question/32610217
#SPJ11
1. Jenna measures all the angles around a point.
Her results are 23°, 145°, 23° and 69°
Explain why these results cannot be true.
Answers
Answer:
When we add 23°, 145°, 23° and 69° we get 260°
And 260° does not have defined number of sides
Step-by-step explanation:
These are the polygons with the number of sides and angles
Polygon Name | Number of Interior Angles | Sum of Interior Angles
Triangle 3 180°
Quadrilateral 4 360°
Pentagon 5 540°
Hexagon 6 720°
Septagon 7 900°
Octagon 8 1080°
Nonagon 9 1260°
Decagon 10 1440°
PLease help, (last Mistake) -_-

Answers
Answer:
B.61kg
Step-by-step explanation:
use the formula
force÷acceleration=mass
183÷3=61kg
Given the equation of y-1=-9/2(x+7) what is the slope of any line parallel? M= blank
Answers
Answer:
Step-by-step explanation:
y - 1 = -9/2 (x + 7)
Distribute -9/2:
y - 1 = -9/2x - 63/2
Add 1 on both sides to isolate y:
(y - 1) + 1 = (-9/2x - 63/2) + 1
y = -9/2x -61/2
A line parallel to another has the same slope as that line so both slopes are -9/2.
M = -9/2
any negative integer less than -5
Answers
Answer:
-6
Step-by-step explanation:
Math, thats how it works.
that’s exactly how it goes yk, that’s the right answer
HELPPPPPPPPPPPP PLSSSSSSS

Answers
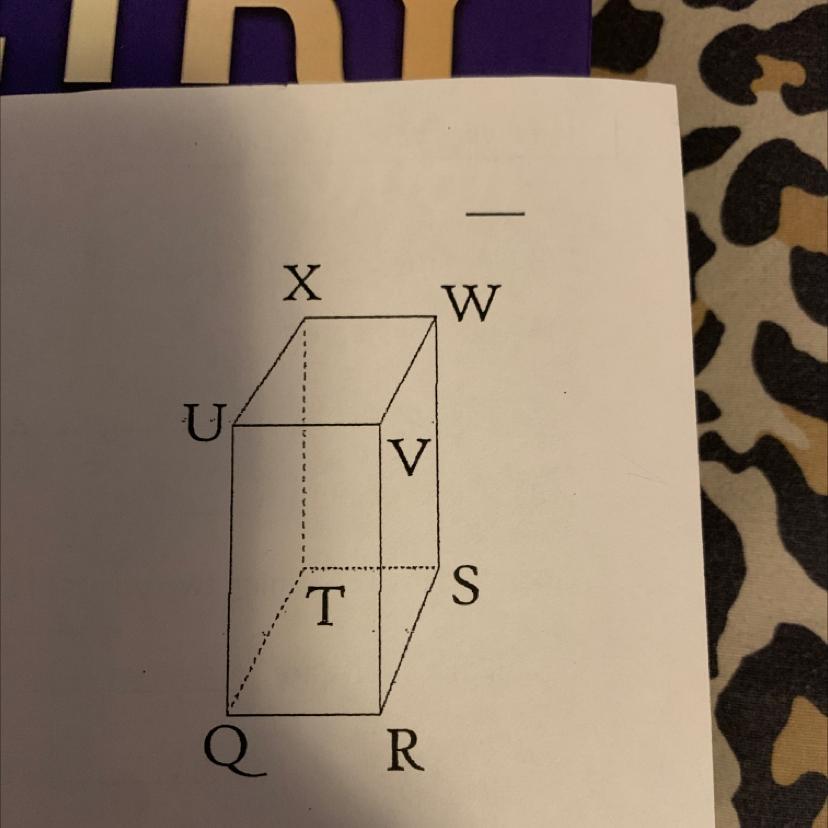
(17-20)Name the intersection of each pair of planes.
Use the figure at the right to help you find the answers.
17.) planes QRS and RSW
18.) planes UXV and WVS
19.) planes XWV and UVR
20.) planes TXW and TQU
Answers
A point of intersection of two or more planes is the point where the plane meet. The answers to the questions are:
17) Point S
18) Point V
19) Point V
20) Point T
A plane is a flat surface which lies or can either be considered with respect to the x- axis, y- axis or z- axis. An intersection of two planes implies the point where the two planes meet.
From the given figure, the given planes has their points of intersections. Thus, the intersection of the planes given in the question are as follows:
17) planes QRS and RSW - The point of intersection of these two planes is point S.
18) planes UXV and WVS - The two planes has the point of their intersection as V.
19) planes XWV and UVR - The point of intersection of the planes is V.
20) planes TXW and TQU - The two planes intersect at point T.
Each of these planes has to be considered separately before relating it to another plane.
Visit: https://brainly.com/question/18753344
how many bit strings of length seven either begin with two 0s or end with three 1s?
Answers
There are 40 such bit strings.
To count the number of bit strings of length seven that either begin with two 0s or end with three 1s, we need to use the principle of inclusion-exclusion.
Let A be the set of bit strings that begin with two 0s, and let B be the set of bit strings that end with three 1s.
Then, we want to find the size of the set A ∪ B, which consists of bit strings that satisfy either condition.
The size of A can be calculated as follows:
since the first two digits must be 0, the remaining five digits can be any combination of 0s and 1s,
so there are \(2^5 = 32\) possible strings that begin with two 0s.
Similarly, the size of B can be calculated as follows:
since the last three digits must be 1, the first four digits can be any combination of 0s and 1s,
so there are\(2^4 = 16\) possible strings that end with three 1s.
However, we have counted the strings that both begin with two 0s and end with three 1s twice.
To correct for this, we need to subtract the number of strings that belong to both A and B from the total count.
The strings that belong to both A and B must begin with two 0s and end with three 1s, so they have the form 00111xxx,
where the x's can be any combination of 0s and 1s.
There are \(2^3 = 8\) such strings.
Therefore, the total number of bit strings of length seven that either begin with two 0s or end with three 1s is:
|A ∪ B| = |A| + |B| - |A ∩ B| = 32 + 16 - 8 = 40.
For similar question on combination.
https://brainly.com/question/11732255
#SPJ11
what is one fourth times one fourth in fraction form
Answers
One fourth times one fourth can be represented as (1/4) * (1/4) in fraction form.
To multiply fractions, we need to multiply the numerators (top numbers) together and the denominators (bottom numbers) together.
In this case, the numerator is 1 * 1, which equals 1. The denominator is 4 * 4, which equals 16.
So, (1/4) * (1/4) is equal to 1/16.
To know more about fraction here:
brainly.com/question/25101057
#SPJ11
Weiming invests S4000 in a savings scheme that pays simple interest at a rate of 2% per annum.
Calculate the time taken for his investment to grow to $4400.
Answers
Answer:
55 YRS
Step-by-step explanation:
T=INTEREST X 100%/PRINCIPAL X RATE
T=4400X100%=440000%/4000 X 2%
T=440000%/8000%
T=55 YRS
Please answer it now in two minutes

Answers
Answer:
Area of the triangle WXY = 365.3 mm²
Step-by-step explanation:
By applying Sine rule in the given triangle XYW,
\(\frac{\text{SinY}}{\text{WX}}=\frac{\text{SinX}}{\text{YW}}\)
\(\frac{\text{Sin70}}{\text{WX}}=\frac{\text{Sin43}}{\text{24}}\)
WX = \(\frac{24.\text{Sin70}}{\text{Sin43}}\)
= 33.068 mm
= 33.07 mm
Area of a triangle = \(\frac{1}{2}a.b.\text{Sin}\theta\)
where a and b are the sides of the triangle and θ is the angle between the sides a and b.
Area = \(\frac{1}{2}(33.07)(24)\text{SinW}\)
Since, m∠X + m∠Y + m∠W = 180°
m∠W = 180 - (43 + 70)
= 67°
Area of the triangle WXY = \(12\times (33.07)\text{Sin67}\)
= 365.29 mm²
≈ 365.3mm²
the perimeter of a rectangle garden is 43.8 ft it's length is 12.4 ft what is the width
Answers
Answer:
9.5 ft
Step-by-step explanation:
Since it is a rectangle. The lengths are the same and the widths are the same.
12.4 + 12.4 = 24.8
43.8 - 24.8 = 19
19/2 = 9.5
Seventeen-year-old Simon went through a period of conflict over issues relating to his identity, but now he feels comfortable with the choices and commitment he has made. Thomas has achieved what Erik Erikson would call:
Answers
Seventeen-year-old Simon went through a period of conflict over issues relating to his identity, but now he feels comfortable with the choices and commitment he has made. Thomas has achieved what Erik Erikson would call: integrated identity
Thomas has achieved what Erik Erikson would call "identity achievement." Erikson's theory of psychosocial development proposes that during adolescence, individuals go through a stage called identity versus role confusion.
This stage is marked by a period of conflict and exploration in which adolescents seek to establish a sense of identity and make meaningful life choices.
Identity achievement refers to the successful resolution of this conflict, where individuals have gone through a process of exploration, self-reflection, and decision-making, ultimately arriving at a clear and coherent sense of self. They have made commitments to particular values, beliefs, relationships, and life goals, and feel a sense of comfort and confidence in their choices.
In the case of seventeen-year-old Simon, who has experienced conflict but now feels comfortable with his choices and commitments, he has likely reached the stage of identity achievement according to Erikson's theory. He has successfully navigated the complexities of adolescence and emerged with a clear and solid sense of his own identity.
Learn more about Psychosocial Development at
brainly.com/question/30767812
#SPJ4
Complete Question:
Seventeen-year-old Simon has gone through a period of conflict over issues relating to his identity, but now he feels comfortable with the choices and commitment he has made. Thomas has achieved what Erikson would call a(n): ___________.
rfggdgdgedrdgd
ggdgdgdgdrgdgdgd
Answers
Answer:
rrfgggefgegeegfegefegegeegfgfgfdfefdfefgdfdfdddgedgdfdgedfgfedffdddfgfdgddfddfgdfdgdf
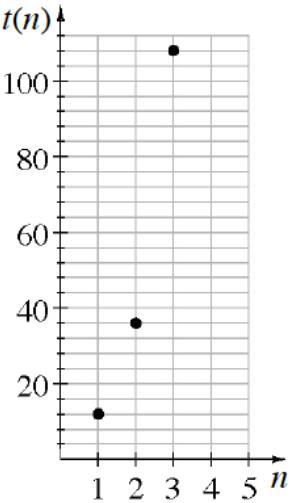
Write an explicit equation for the sequence based on the graph at right.
Answers
Answer:
\(t(n)=12 \cdot 3^{n-1}\)
Step-by-step explanation:
From inspection, the points on the graph are:
(1, 12)(2, 36)(3, 108)Therefore, as terms of a sequence:
\(t_1=12\\\\t_2=36\\\\t_3=108\)
The difference between the y-coordinates is not equal, therefore the sequence is geometric.
Geometric sequence formula: \(t_n=t_1r^{n-1}\)
As \(t_1=12 \implies t_n=12r^{n-1}\)
To find r, divide one term by the previous term:
\(r=\dfrac{t_3}{t_2}=\dfrac{108}{36}=3\)
Therefore, geometric sequence formula: \(t_n=12 \cdot 3^{n-1}\)
Standard Questions
Question Progress
The average mass of a man is 84 kg and of a woman is 70 kg.
A lift can safely carry 720 kg.
Work out the maximum number of people the lift can safely carry.
Answers
We need to know simple division to solve the problem. The maximum number of men in the lift is 8 and the maximum number of women in the lift is 10.
We will be using the simple concept of division to find the number of people that the lift can carry. The average weight of a man is given to be 84 kg and the average weight of a woman is given to be 70kg. The lift can carry 720 kg, we will find separately the number of men and women that can be carried in the lift. Inorder to find the maximum number of men we divide the total weight the lift can carry by the average weight of a man, we will similarly calculate the maximum number of women.
number of men= 720/84=8.57 which means that the number of men is 8
number of women =720/70=10.28 which means that number of women is 10.
Therefore the lift can carry at most 8 men and at most 10 women.
Learn more about division here:
https://brainly.com/question/25289437
#SPJ1
!GIVING BRAINLIST! PLEASE HELP
Drag the labels to the correct location on the table. Each label can be used more than once.
Identify the correct rhyme scheme for each excerpt.
abab
abcb
aabb

Answers
Answer:
For the first excerpt, the rhyme scheme is ABAB
For the second excerpt, the rhyme scheme is ABCB
For the third it is, AABB
For the Fourth it is, ABAB
For the Fifth it is, ABCB
Step-by-step explanation:
Hope this helped
A brainliest is always appreciated.
Simplify
5 + 2(3x − 4) − x
Answers
\(5x - 3\)
Step-by-step explanation:
1) Expand by distributing terms.
\(5 + 6x - 8 - x\)
2) Collect like terms.
\((5 - 8) + (6x - x)\)
3) Simplify.
\( - 3 + 5x\)
4) Regroup terms.
\(5x - 3\)
Therefor the answer for this equation will be, 5x - 3.
Answer:
5x-3
Step-by-step explanation:
distribute 2 to 3x and -4
then you get 5+6x-8-x
combine like terms
5-8; 6x-x
you get: 5x-3
hopes this helps
A cyclist took 180 min to cover a 38-km course. For the first 29 km, he cycled at a speed of 15 kph. Find his speed for the remaining 26 km of the course. ( show solution please )
Answers
His speed for the remaining 26 km of the course is given as follows:
24.3 km/h.
What is the relation between velocity, distance and time?The relation between velocity, distance and time states that the velocity is obtained by the quotient of the distance by the time, as follows:
v = d/t.
In which the parameters are given as follows:
v is the velocity.d is the distance.t is the time.The time is obtained as the distance divided by the velocity, hence:
t = d/v.
Then the time taken for the first 29 km is given as follows:
t = 29/15
t = 1.93 hours.
180 minutes = 3 hours, hence he took 1.07 hours for the remaining 26 km, hence the velocity is of:
v = 26/1.07
v = 24.3 km/h.
More can be learned about velocity, distance and time at brainly.com/question/4931057
#SPJ1
what+is+the+present+value+of+annual+$8,848+payments+over+the+upcoming+5+years+,on+an+interest+rate+of+10%?
Answers
The present value of $8,848 annual payments over the next 5 years at an interest rate of 10% is approximately $33540.88.
The present value of an annuity is a measure of its worth today, taking into account the time value of money and the rate of interest. To calculate the present value, each future payment is discounted back to the present day.
In this case, with an interest rate of 10%, each $8,848 payment is worth less in today's dollars the further out it is made. The present value of these payments over the next 5 years would be the sum of the present value of each payment, which is approximately $33540.88.
To know more about annuity click on below link:
https://brainly.com/question/23554766#
#SPJ11
calculate least squares solution using svd a matrix has the singular value decomposition what is the solution to the least-squares problem that has minimal norm ?
Answers
The Least-squares problem that has minimal norm can be given using factorization.
The least squares method is used to find the best fit for a set of data points by minimizing the sum of the offsets from the plotted curve. Singular value decomposition (SVD) is a factorization of a real or complex matrix.
It is a widely used technique to decompose a matrix into several component matrices, exposing many of the useful and interesting properties of the original matrix. The singular value decomposition, guaranteed to exist, is A=UΣV.
When we have the equation system Ax=b, we calculate the SVD of A as A=UΣVT. The matrices U and VT have a very special property. They are unitary matrices. One of the main benefits of having unitary matrices like U and VT is that if we multiply one of these matrices by its transpose (or the other way around), the result equals the identity matrix.
The singular value decomposition (SVD) of matrix A is very useful in the context of least squares problems. It is also very helpful for analyzing the properties of a matrix.
To know more about the Least square method,
brainly.com/question/22513087
brainly.com/question/29560177
#SPJ4
At Total Viewing, the
wholesale price of a 52-inch television is
$1.950. What does it cost to buy the
television if the store's markup is 15%?
Answers
Answer:
It would be 2242.5
Step-by-step explanation:
1950X0.15=292.5
292.5+1950=2242.5
PLSS?? HELP??? ALGEBRA: EIGHTH GRADE EDITION

Answers
Answer:
y = -\(\frac{2}{5}\)x + 9
Step-by-step explanation:
slope-intercept form is y = mx + b, where m is the slope and b is the y-intercept
an equation with the SLOPE (m) of -\(\frac{2}{5}\) and Y-INTERCEPT (b) of 9 would be
y = -\(\frac{2}{5}\)x + 9
What is an equation of the line that passes through the points of (8,-7) and (-6,-7)
Answers
Answer: y+7=0 x(x-8)
Step-by-step explanation:
.
Help me on this question please help this is due

Answers
Answer:
1.50 1.5
Step-by-step explanation:
beacuse its both of the wingspans together
Answer:
i think 1.5 inch
Step-by-step explanation:
0.75*2
this is because 1 wing is . 75 inch ACROSS so if two wings you will multiply it into two
A new miniature golf and arcade opened up in town. For convenient ordering, a play package is available to purchase. It includes two rounds of golf and 20 arcade tokens, plus $3.00 off the regular price. Stacey and her six friends are purchasing this package. Let g represent the cost of a round of golf, and let t represent the cost of a token. Write two different expressions that represent the total amount this group spent.
Answers
Answer:
a. 7(2g + 20t –3)
b. 14g + 140t – 21
Step-by-step explanation:
a. The first expression 7(2g + 20t – 3)
Stacey and her six friends implies that we have 7 members in the group.
Therefore, the expression above implies that each member of the group has to pay for two rounds of golf and 20 tokens will be discounted $3.00.
The expression (2g + 20t –3) represents the quantity of cost of each friend and this is multiplied by 7 to obtain this first expression, i.e. 7(2g + 20t –3).
b. The second expression 14g + 140t – 21
The simple interpretation of this expression us that deducting $21 from the to total bill which is 14 games of golf plus 140 tokens is equal to the total amount this group spent.
Therefore, this second expression is obtained by simply opening the bracket in the first expression by multiplying 7 by each of the what is in the bracket.
Find the probability of exactly three
successes in eight trials of a binomial
experiment in which the probability of
success is 45%.
, or the probability of failure, as a decimal.
Enter q,
9
= [?]
Enter

Answers
Answer:
q = 0.55p(3 of 8) = 0.2568Step-by-step explanation:
You want q and the probability of 3 successes in 8 trials if the probability of success is 0.45.
QThe value designated q is the complement of p, the probability of success.
q = 1 -p
q = 1 -0.45
q = 0.55
P(3 of 8)The probability of 3 successes is ...
P(3 of 8) = 8C3·p^3·q^(8-3) = 56·0.45^3·0.55^5
P(3 of 8) ≈ 56°0.091125·0.050328 ≈ 0.256826
The probability of exactly 3 successes in 8 trials is about 0.2568.
<95141404393>

abc is a right triangle with ab=ac. bisector of <a meets bc at d. prove that bc = 2ad.
Answers
Answer:
Let ac=ab=5
With this, bc= 5√2
Step-by-step explanation:
So to find ad, Let ad be x
5√2=(2)(x)
(5√2/2)= x
This proves that bc=2ad
