What is the solution to this system of equations -3x+5y=-2
3x+7y=26
Answers
Answer: -3x+5y=-2 = x=5/3y+2/3
3x+7y=26 = x=-7/3y+26/3
Step-by-step explanation:
Answer:
A (4,2)
Step-by-step explanation:
edge
Related Questions
determine whether the numerical value is a parameter or a statistic the average salary of all assembly-line employees at a certain car manufacturer is $ 44,000
Answers
The given numerical value of $44,000 represents the average salary of all assembly-line employees at a certain car manufacturer. Hence, it is a parameter.
In statistical analysis, the terms "parameter" and "statistic" are used to distinguish between population characteristics and sample characteristics, respectively. To determine whether the given numerical value represents a parameter or a statistic, we need to understand the context in which the value is used.
A parameter refers to a numerical value that describes a characteristic of a population. It represents a fixed, unknown value and is typically denoted by Greek letters. Parameters are derived from data collected from an entire population.
On the other hand, a statistic refers to a numerical value that describes a characteristic of a sample. It is computed from a subset of data, known as a sample, and is used to estimate the corresponding population parameter.
In the given statement, the average salary of all assembly-line employees at a certain car manufacturer is stated to be $44,000. Since this value represents the average salary of all employees in the population, it is a parameter. The value is derived from information about the entire population of assembly-line employees at the car manufacturer, rather than a sample.
If the statement had mentioned the average salary of a sample of assembly-line employees, then the numerical value would have been a statistic. In that case, it would have been computed from a subset of the data (a sample) and used to estimate the average salary of the entire population.
In summary, the given numerical value of $44,000 represents the average salary of all assembly-line employees at a certain car manufacturer. Hence, it is a parameter.
for more such question onparameter visit
https://brainly.com/question/29344078
#SPJ8
write the rational number as a decimal, and state whether the decimal is repeating or terminating. question content area bottom part 1 choose the equivalent decimal. a. 0. b. 0. c.0. 16 overbar d. 0.
Answers
a. The decimal is terminating and the rational number is 0.
b. The decimal is terminating and the rational number is 0.
c. The decimal is repeating and the rational number is 0.161616...
d. The decimal is terminating and the rational number is 0.
To write a rational number as a decimal, you need to divide the numerator by the denominator. Let's go through each option to determine which decimal is repeating or terminating.
a. 0: This decimal is terminating because there are no numbers after the decimal point. The rational number is 0.
b. 0: This decimal is also terminating because there are no numbers after the decimal point. The rational number is 0.
c. 0.16 overbar: This decimal has a line over the 16, indicating that it is repeating. The rational number is 0.161616...
d. 0: This decimal is terminating because there are no numbers after the decimal point. The rational number is 0.
So, to summarize:
a. The decimal is terminating and the rational number is 0.
b. The decimal is terminating and the rational number is 0.
c. The decimal is repeating and the rational number is 0.161616...
d. The decimal is terminating and the rational number is 0.
.
To know more about rational number refer here:
https://brainly.com/question/24398433
#SPJ11
Solve for Y Next, find the side lengths of the
medium-sized triangle

Answers
Answer:
Y = √80 or 4√5
Step-by-step explanation:
According to the combined triangle, the green area would be 8. Since it is a right triangle, we can use the Pythagorean theorem: a² + b² = c²
in this case, y would be the hypotenuse, or C in the equation.
thus, the equation would be:
4² + 8² = C² where C is Y
16 + 64 = C²
80 = C²
√80 = √C²
C = √80 or 4√5
Y = √80 or 4√5
I hope this helped you!
what is
7d+6)-(-3d-5) ?
Answers
\((7d+6)-(-3d-5) \\ \\ =7d+6+3d+5 \\ \\ =\boxed{10d+11}\)
from a large group of people who signed a card saying they intended to quit smoking, 1000 people were selected at random. it turned out that 210 (21%) of these individuals had not smoked over the past 6 months. what is the parameter of interest?
Answers
The parameter of interest is the proportion of people in the original group who had not smoked over the past 6 months.
We can calculate the parameter of interest by taking the number of people in the sample who had not smoked over the past 6 months (210) and dividing it by the total number of people in the sample (1000). This gives us a proportion of 0.21, or 21%. This tells us that 21% of people in the original group had not smoked over the past 6 months. This proportion is the parameter of interest in this scenario.
210/1000 = 0.21 or 21%
Learn more about parameter here
https://brainly.com/question/13794992
#SPJ4
Pls help me I am so confused and nobody has been helping me
You choose two different side items on a menu at random. Out of 9 side
items on the menu, 3 are vegetables. The first side item you choose is a
vegetable. What is the probability that the second is also a vegetable?
Answers
Answer:
1/4
Step-by-step explanation:
You want the probability that a random choice from a menu of 9 items, including 3 vegetables, is a vegetable after one vegetable has already been chosen. The second choice is different from the first.
MenuAfter choosing one vegetable, the available different items remaining on the menu are 2 vegetables among a total of 8 items.
The probability that the second random choice will be a vegetable is ...
(2 vegetables)/(8 items) = 2/8 = 1/4
The probability that the second choice is also a vegetable is 1/4.
__
Additional comment
Since the choices must be different, the first choice is essentially removed from the menu. Since we're only concerned with the second choice, we don't need to consider the probability that the first choice was a vegetable.
show that (1 − x − x 2 − x 3 − x 4 − x 5 − x 6) −1 is the generating function for the number of ways a sum of r can occur if a die is rolled any number of times
Answers
1 - x - x² - x³ - x⁴ - x⁵ - x⁶ can be shown generating number of ways considering number of die rolls as infinite series and showing that expression is equivalent to the generating function.
To show that (1 - x - x² - x³ - x⁴ - x⁵ - x⁶)-¹ is the generating function for the number of ways a sum of r can occur if a die is rolled any number of times, we'll follow these steps:
1. Identify the generating function for a single die roll.
2. Consider the infinite series representing any number of die rolls.
3. Show that the given expression is equivalent to the generating function.
Step 1: For a single die roll, the possible outcomes are 1, 2, 3, 4, 5, and 6. The generating function representing this is:
F(x) = x + x²+ x³ + x⁴+ x⁵+ x⁶
Step 2: To consider any number of die rolls, we want to find the generating function that represents the sum of outcomes for an infinite number of rolls. This is the sum of the geometric series with a common ratio F(x), so the infinite series is:
G(x) = 1 + F(x) + F(x)² + F(x)³ + ...
Step 3: To show that the given expression is equivalent to the generating function, we want to show that G(x) = (1 - x - x² - x³- x⁴- x⁵ - x⁶)-¹.
We know that the sum of an infinite geometric series is:
Sum = 1 / (1 - r)
Here, r = F(x), so the sum of the series G(x) is:
G(x) = 1 / (1 - F(x))
Now, substitute F(x) from Step 1:
G(x) = 1 / (1 - (x + x²+ x³+ x⁴+ x⁵ + x⁶))
G(x) = 1 / (1 - x - x² - x³- x⁴- x⁵- x⁶)
Thus, we have shown that (1 - x - x²- x³ - x⁴ - x⁵ - x⁶)-¹ is the generating function for the number of ways a sum of r can occur if a die is rolled any number of times.
Learn more about infinite series : https://brainly.com/question/29098051
#SPJ11
Which construction can be used to find a line thatis perpendicular to line AB that passes throughpoint P ?PV*BX ХPBPАBPXAB


Answers
Recall that a line A is perpendicular to a line B if they form a 90 degrees angle, as in the picture below:
Therefore, the only construction of the ones given that can be used to find a perpendicular line to AB is the second option.

In Problems 1 through 12, verify by substitution that each given function is a solution of the given differential equation. Throughout these problems, primes denote derivatives with re- spect to x. 1. y' = 3x2; y = x³ +7 2. y' + 2y = 0; y = 3e-2x 3. y" + 4y = 0; y₁ = cos 2x, y2 = sin 2x 4. y" = 9y; y₁ = e³x, y₂ = e-3x 5. y' = y + 2e-x; y = ex-e-x 6. y" +4y^ + 4y = 0; y1= e~2x, y2 =xe-2x 7. y" - 2y + 2y = 0; y₁ = e cos x, y2 = e* sinx 8. y"+y = 3 cos 2x, y₁ = cos x-cos 2x, y2 = sinx-cos2x 1 9. y' + 2xy2 = 0; y = 1+x² 10. x2y" + xy - y = ln x; y₁ = x - ln x, y2 = =-1 - In x In x 11. x²y" + 5xy' + 4y = 0; y1 = 2 2 = x² 12. x2y" - xy + 2y = 0; y₁ = x cos(lnx), y2 = x sin(In.x)
Answers
The solutions to the given differential equations are:
y = x³ + 7y = 3e^(-2x)y₁ = cos(2x), y₂ = sin(2x)y₁ = e^(3x), y₂ = e^(-3x)y = e^x - e^(-x)y₁ = e^(-2x), y₂ = xe^(-2x)y₁ = e^x cos(x), y₂ = e^x sin(x)y₁ = cos(x) - cos(2x), y₂ = sin(x) - cos(2x)y = 1 + x²y₁ = x - ln(x), y₂ = -1 - ln(x)y₁ = x², y₂ = x^(-2)y₁ = xcos(ln(x)), y₂ = xsin(ln(x))To verify that each given function is a solution of the given differential equation, we will substitute the function into the differential equation and check if it satisfies the equation.
1. y' = 3x²; y = x³ + 7
Substituting y into the equation:
y' = 3(x³ + 7) = 3x³ + 21
The derivative of y is indeed equal to 3x², so y = x³ + 7 is a solution.
2. y' + 2y = 0; y = 3e^(-2x)
Substituting y into the equation:
y' + 2y = -6e^(-2x) + 2(3e^(-2x)) = -6e^(-2x) + 6e^(-2x) = 0
The equation is satisfied, so y = 3e^(-2x) is a solution.
3. y" + 4y = 0; y₁ = cos(2x), y₂ = sin(2x)
Taking the second derivative of y₁ and substituting into the equation:
y"₁ + 4y₁ = -4cos(2x) + 4cos(2x) = 0
The equation is satisfied for y₁.
Taking the second derivative of y₂ and substituting into the equation:
y"₂ + 4y₂ = -4sin(2x) - 4sin(2x) = -8sin(2x)
The equation is not satisfied for y₂, so y₂ = sin(2x) is not a solution.
4. y" = 9y; y₁ = e^(3x), y₂ = e^(-3x)
Taking the second derivative of y₁ and substituting into the equation:
y"₁ = 9e^(3x)
9e^(3x) = 9e^(3x)
The equation is satisfied for y₁.
Taking the second derivative of y₂ and substituting into the equation:
y"₂ = 9e^(-3x)
9e^(-3x) = 9e^(-3x)
The equation is satisfied for y₂.
5. y' = y + 2e^(-x); y = e^x - e^(-x)
Substituting y into the equation:
y' = e^x - e^(-x) + 2e^(-x) = e^x + e^(-x)
The equation is satisfied, so y = e^x - e^(-x) is a solution.
6. y" + 4y^2 + 4y = 0; y₁ = e^(-2x), y₂ = xe^(-2x)
Taking the second derivative of y₁ and substituting into the equation:
y"₁ + 4(y₁)^2 + 4y₁ = 4e^(-4x) + 4e^(-4x) + 4e^(-2x) = 8e^(-2x) + 4e^(-2x) = 12e^(-2x)
The equation is not satisfied for y₁, so y₁ = e^(-2x) is not a solution.
Taking the second derivative of y₂ and substituting into the equation:
y"₂ + 4(y₂)^2 + 4y₂ = 2e^(-2x) + 4(xe^(-2x))^2 + 4xe^(-2x) = 2e^(-2x) + 4x^2e^(-4x) + 4xe^(-2x)
The equation is not satisfied for y₂, so y₂ = xe^(-2x) is not a solution.
7. y" - 2y + 2y = 0; y₁ = e^x cos(x), y₂ = e^x sin(x)
Taking the second derivative of y₁ and substituting into the equation:
y"₁ - 2(y₁) + 2y₁ = e^x(-cos(x) - 2cos(x) + 2cos(x)) = 0
The equation is satisfied for y₁.
Taking the second derivative of y₂ and substituting into the equation:
y"₂ - 2(y₂) + 2y₂ = e^x(-sin(x) - 2sin(x) + 2sin(x)) = 0
The equation is satisfied for y₂.
8. y" + y = 3cos(2x); y₁ = cos(x) - cos(2x), y₂ = sin(x) - cos(2x)
Taking the second derivative of y₁ and substituting into the equation:
y"₁ + y₁ = -cos(x) + 2cos(2x) + cos(x) - cos(2x) = cos(x)
The equation is not satisfied for y₁, so y₁ = cos(x) - cos(2x) is not a solution.
Taking the second derivative of y₂ and substituting into the equation:
y"₂ + y₂ = -sin(x) + 2sin(2x) + sin(x) - cos(2x) = sin(x) + 2sin(2x) - cos(2x)
The equation is not satisfied for y₂, so y₂ = sin(x) - cos(2x) is not a solution.
9. y' + 2xy² = 0; y = 1 + x²
Substituting y into the equation:
y' + 2x(1 + x²) = 2x³ + 2x = 2x(x² + 1)
The equation is satisfied, so y = 1 + x² is a solution.
10 x²y" + xy' - y = ln(x); y₁ = x - ln(x), y₂ = -1 - ln(x)
Taking the second derivative of y₁ and substituting into the equation:
x²y"₁ + xy'₁ - y₁ = x²(0) + x(1) - (x - ln(x)) = x
The equation is satisfied for y₁.
Taking the second derivative of y₂ and substituting into the equation:
x²y"₂ + xy'₂ - y₂ = x²(0) + x(-1/x) - (-1 - ln(x)) = 1 + ln(x)
The equation is not satisfied for y₂, so y₂ = -1 - ln(x) is not a solution.
11. x²y" + 5xy' + 4y = 0; y₁ = x², y₂ = x^(-2)
Taking the second derivative of y₁ and substituting into the equation:
x²y"₁ + 5xy'₁ + 4y₁ = x²(0) + 5x(2x) + 4x² = 14x³
The equation is not satisfied for y₁, so y₁ = x² is not a solution.
Taking the second derivative of y₂ and substituting into the equation:
x²y"₂ + 5xy'₂ + 4y₂ = x²(4/x²) + 5x(-2/x³) + 4(x^(-2)) = 4 + (-10/x) + 4(x^(-2))
The equation is not satisfied for y₂, so y₂ = x^(-2) is not a solution.
12. x²y" - xy' + 2y = 0; y₁ = xcos(ln(x)), y₂ = xsin(ln(x))
Taking the second derivative of y₁ and substituting into the equation:
x²y"₁ - xy'₁ + 2y₁ = x²(0) - x(-sin(ln(x))/x) + 2xcos(ln(x)) = x(sin(ln(x)) + 2cos(ln(x)))
The equation is satisfied for y₁.
Taking the second derivative of y₂ and substituting into the equation:
x²y"₂ - xy'₂ + 2y₂ = x²(0) - x(cos(ln(x))/x) + 2xsin(ln(x)) = x(sin(ln(x)) + 2cos(ln(x)))
The equation is satisfied for y₂.
Therefore, the solutions to the given differential equations are:
y = x³ + 7
y = 3e^(-2x)
y₁ = cos(2x)
y₁ = e^(3x), y₂ = e^(-3x)
y = e^x - e^(-x)
y₁ = e^(-2x)
y₁ = e^x cos(x), y₂ = e^x sin(x)
y = 1 + x²
y₁ = xcos(ln(x)), y₂ = xsin(ln(x))
Learn more about differential equation
https://brainly.com/question/32538700
#SPJ11
1 subtract 3/4 help please!!
Answers
Answer: 1/4
Step-by-step explanation: 1-3/4
Answer: 1 subtracted by 3/4 is -0.25 (Decimal form) but as a fraction, it's -1/4. (Fraction form)
If this is not what you want or doesn't help. Just let me know and I'll see what I can do!
which of the following statistics determines whether there are differences between two nominally scaled variables?
Answers
The chi-square statistic is used to determine whether there are differences between two nominally scaled variables. Chi-Square is a statistical test used to compare two nominal variables to determine whether they differ.
The Chi-Square test is used to test for differences between two groups. When you want to compare groups or examine the relationship between two variables, this test is useful. The chi-square test is a method of statistical inference that can be used to compare observed frequencies with expected frequencies, allowing us to determine whether there is a meaningful difference between them. When the p-value obtained from a chi-square test is less than 0.05, it is generally considered statistically significant.
Learn more about Chi-Square
https://brainly.com/question/32595988
#SPJ11
15. Richie and Justin are doing house renovations for Kirk. Kirk has promised them at least 20 total hours of
work per week, but can pay them no more than $1,200 per week of total wages, Richie makes $25 per hour
and Justin makes $45 per hour.
Letting x be the number of hours Richie works and y be the number of hours Justin works, write a system of
inequalities that models this situation.
Answers
25x + 45y ≤ 1,200
25x representing how much Richie would get paid in total (x representing the hours), 45y representing how much Justin would get paid in total (y representing the hours), ≤ representing less than or equal to, 1,200 is the greatest amount that Kirk can pay.
2
Which equation describes a linear function?
O 4x2 + 5y2 = 6
+
O 4r + 5y = 6
0 4x² + 5y = 6
4x + 5y2 = 6
Answers
Answer:
See below.
Step-by-step explanation:
The answer is 4x+5y=6.
A linear function has a single slope. A function with exponents will not be linear.
-hope it helps
Three segments (a, b, and c) of trump enterprises have net sales of $300,000, $150,000, and $50,000, respectively. a decision is made to allocate the pool of $25,000 of administrative overhead expenses of the home office to the segments, using net sales as the basis for allocation.
Answers
Three segments a, b, and c using net sales as the basis for allocation is = $475,000.
Based on the given conditions,
Three segments are a , b , c
The segment a of trump enterprises have net sales = $300,000
The segment b of trump enterprises have net sales = $150,000
The segment c of trump enterprises have net sales = $50,000
a net sales + b net sales + c net sales = $300,000 + $150,000 + $50,000
= $500,000
If the unit is eliminated, then the a net sales and b net sales will be gone, but the c net sales will be allocated to other business units.
So instead of losing $500,000,
A decision is made to allocate the pool = $25,000
The company's net sales as the basis for allocation by $500,000 - $25,000 = $475,000
Therefore,
Three segments a, b, and c using net sales as the basis for allocation is =
$475,000.
To learn more about information visit Net sales :
brainly.com/question/12983001
#SPJ4
What is the following product? StartRoot 12 EndRoot times StartRoot 18 EndRoot StartRoot 30 EndRoot
Answers
Answer:
\( 6\sqrt{6} \)
Step-by-step explanation:
\( \sqrt{12}\sqrt{18} = \)
\( = \sqrt{12 \cdot 18} \)
\( = \sqrt{4 \cdot 3 \cdot 9 \cdot 2} \)
\( = \sqrt{36 \cdot 6} \)
\( = \sqrt{36}\sqrt{6} \)
\( = 6\sqrt{6} \)
Following are the step by step solutions to the given expression:
Given:
\(\to \sqrt{12} \times \sqrt{18} \sqrt{30}\)
To find:
solve=?
Solution:
\(\to \sqrt{12} \times \sqrt{18} \sqrt{30}\)
\(\to \sqrt{2\times 2 \times 3} \times \sqrt{2\times 3 \times 3} \sqrt{2 \times 3 \times 5} \\\\ \)
\(\to 2\sqrt{3} \times 3\sqrt{2} \sqrt{2 \times 3 \times 5} \\\\ \to 6\times \sqrt{3} \times \sqrt{2} \sqrt{2\times 3 \times 5} \\\\ \to 6\times \sqrt{3} \times \sqrt{2} \times \sqrt{2}\times \sqrt{3} \times \sqrt{5} \\\\ \to 6 \times 3 \times 2 \times \sqrt{5} \\\\ \to 36 \sqrt{5}\)
Therefore, the final answer is "\(36\sqrt{5}\)"
Learn more:
brainly.com/question/24050871
For a moving object, the force acting on the object varies directly with the object's acceleration. When a force of 90 N acts on a certain object, the acceleration of the object is 10 m/s² . If the force is changed to 81N , what will be the acceleration of the object?
Answers
Answer:
9 1/10th m/s2 :)
Step-by-step explanation:
The reason it is 1/10 is because the Number is 81 not 80, therefore 1/10 because there it is 1 left in 80 making it a fraction not a whole :) i hope this helps sorry if the explanation is too complicated...
Given point Q equals negative 5 comma negative 5 radical 3 in rectangular coordinates, what are the corresponding polar coordinates?

Answers
The corresponding polar coordinates are (10, 2π/3). Option B
How to determine the valueFrom the information given, we have;
(-5, 5√3)
Given that the polar coordinates are represented as;
r = √(x² + y²)
θ = arctan(y / x)
We get;
\(r = \sqrt{(-5)^2} + (\sqrt{5} /3)^2\)
Find the value of square, we have;
r = \(\sqrt{25 + 75}\)
Add the values, we get;
r = \(\sqrt{100}\)
Find the square root
r = 10
To determine the value of theta, we get;
θ = arctan((-5√3) / -5)
Divide the values, we have;
θ = arctan(√3)
θ = 60 degrees
Then, we have; (10, 2π/3)
Learn more about polar coordinates at: https://brainly.com/question/29012031
#SPJ1
In a data set with a, b, c, d, e, and f numeric variables, given there are strong correlation of these pairs (f, a), (f, c), (d, e), (a, d), we can set up a regression model as:
Of-a + c Of-a + b + c + d + e Of-a + C + d + e Of-a + C + e
Given two predictor variables with correlation at 0.32879, we should expect there is multicollinearity between them.
Answers
Given two predictor variables with a correlation of 0.32879, we should expect there to be multicollinearity between them.
In a data set with a, b, c, d, e, and f numeric variables, given there is a strong correlation of these pairs (f, a), (f, c), (d, e), (a, d), we can set up a regression model as
Of-a + c Of-a + b + c + d + e Of-a + C + d + e Of-a + C + e.
Given two predictor variables with a correlation of 0.32879, we should expect there is multicollinearity between them.
The statement that is true regarding the given two predictor variables with a correlation of 0.32879 is:
we should expect there to be multicollinearity between them.
Multicollinearity is a situation in which two or more predictor variables in a multiple regression model are highly correlated with one another. Multicollinearity complicates the understanding of which predictor variables are significant in the regression model's estimation.
Therefore, given two predictor variables with a correlation of 0.32879, we should expect there to be multicollinearity between them.
To know more about multicollinearity visit:
https://brainly.in/question/7285022
#SPJ11
Two containers designed to hold water are side by side, both in the shape of a cylinder. Container A has a diameter of 14 feet and a height of 9 feet. Container B has a diameter of 10 feet and a height of 20 feet. Container A is full of water and the water is pumped into Container B until Container A is empty. To the nearest tenth, what is the percent of Container B that is empty after the pumping is complete?
Answers
Answer:
11.8 % empty
Step-by-step explanation:
volume of cylinder : pi × r² × h
attention ! the question gives us diameter, so for radius we need to cut them in half.
Va = pi × (14/2)² × 9 = pi×49×9 = 1385.44236... ft³
Vb = pi × (10/2)² × 20 = pi×25×20 = 1570.79633... ft³
after filling B with everything in A there is still some empty volume in B
Vb empty = Vb - Va = 185.35397... ft³
so,
100% Vb = 1570.79633... ft³
1% Vb = 15.7079633... ft³
so, how often does 1% of the total volume of B fit into the remaining empty volume of B ?
185.35397... / 15.7079633... = 11.8%
Which of the following is equivalent to the complex number i^{26}i
26
i, start superscript, 26, end superscript?
Answers
Answer:
-1
Step-by-step explanation:
\(i^{26}\)
= \((i^{2} )^{13}\)
= \((-1)^{13}\)
= -1
The equation below is the equation of a line in point slope form, what is the x-
coordinate of the point?
y+5=—3 (x+6)
Answers
Answer:
Step-by-step explanation:
X=-x^2+x-5
HELP MEE
Use the provided ruler to find the scale and the scale factor of the drawing
Iris
Cornea
Pupil
24 mm
Vitreous
humor
Lens
The scale is
cm :
mm.
The scale factor is
Answers
Answer:
45
Step-by-step explanation:
I took the test and got right
Which polynomial correctly combines the like terms and puts the given polynomial in standard form? one-thirdx 8x4 – two-thirdsx2 – x 8x4 – one-thirdx2 – x 8x4 two-thirdsx2 two-thirdsx 8x4 – two-thirdsx2 – two-thirdsx 8x4 – two-thirdsx2 – x.
Answers
Polynomial equation is a equation which is formed with coefficients variables and exponents with basic mathematics operation and equality sign. From the given option the option C correctly combines the like terms and puts the given polynomial in standard form which is,
\(8x^4-\dfrac{2}{3}x^2-\dfrac{2x}{3}\\\)
Hence the option C is the correct option.
Given information-The given polynomial equation in the problem is,
\(\dfrac{1}{3} x+8x^4-\dfrac{2}{3}x^2-x\)
Polynomial equationPolynomial equation is a equation which is formed with coefficients variables and exponents with basic mathematics operation and equality sign.
In the above polynomial equation the variable are x and the highest power of the variable x is four.
Arrange the given polynomial equation in the power of the variable x. Thus,
\(8x^4-\dfrac{2}{3}x^2+\dfrac{1}{3} x-x\)
Make the group of the same power of the variable x. Therefore,
\(8x^4-\dfrac{2}{3}x^2+(\dfrac{1}{3} x-x)\)
\(8x^4-\dfrac{2}{3}x^2+\dfrac{x-3x}{3}\\\)
\(8x^4-\dfrac{2}{3}x^2-\dfrac{2x}{3}\\\)
From the given option the option C correctly combines the like terms and puts the given polynomial in standard form which is,
\(8x^4-\dfrac{2}{3}x^2-\dfrac{2x}{3}\\\)
Hence the option C is the correct option.
Learn more about the polynomial equation here;
https://brainly.com/question/25958000
PLS HELP! GEOMETRY!!
Find the surface area of each figure. Round your answers to the nearest hundredth, if necessary.
if you're actually willing to help me with my geometry test that would be awesome
Its a win-win!

Answers
Surface area of cuboid is = 312 ,With dedication and effort, you can succeed in your geometry test and feel confident about your understanding of the subject.
Surface area of a cuboid is = 2lw + 2lh + 2 hw
where ; l= length
w= width.
h = height
= 2(10×6)+2(10×6)+2(6×6)
=2(60)+2(60)+2(36)
=120+120+72
=312
Geometry can be challenging, but with the right mindset and approach, you can do well. To start, make sure you understand the basic concepts and definitions.
Then, practice solving problems and applying those concepts. Don't be afraid to ask questions or seek help when you need it. Utilize resources such as textbooks, online tutorials, and practice worksheets.
Also, try to relate geometry to real-life situations to make it more interesting and relevant. Remember to take breaks and stay organized to avoid feeling overwhelmed.
To learn more about : geometry test
https://brainly.com/question/30902501
#SPJ8

does someone mind helping me with this problem? Thank you!
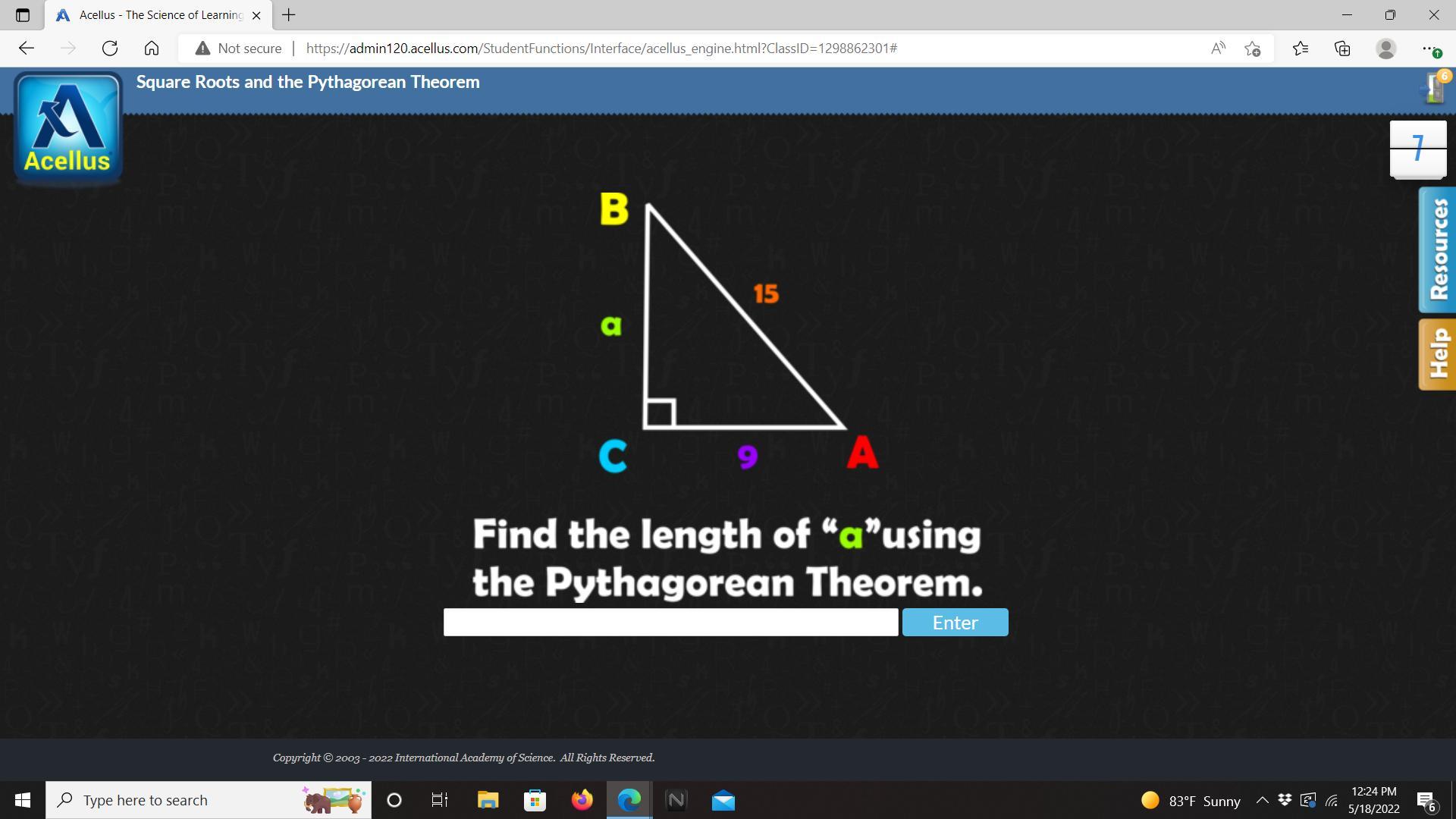
Answers
Answer:
a = 12
Step-by-step explanation:
Pythagoras’ Theorem
a² + b² = c²
(where a and b are the legs, and c is the hypotenuse, of a right triangle)
From inspection of the triangle:
leg a = aleg b = 9hypotenuse c = 15Substituting these values into the formula and solving for b:
⇒ a² + 9² = 15²
⇒ a² + 81 = 225
Subtract 81 from both sides:
⇒ a² + 81 - 81 = 225 - 81
⇒ a² = 144
Square root both sides:
⇒ √(a²) = √(144)
⇒ a = 12
\(\qquad\qquad\huge\underline{{\sf Answer}}\)
Let's calculate the value of a using Pythagoras theorem ~
\(\qquad \sf \dashrightarrow \: c {}^{2} = a {}^{2} + {b}^{2} \)
\(\qquad \sf \dashrightarrow \: a {}^{2} = {15}^{2} - {9}^{2} \)
\(\qquad \sf \dashrightarrow \: a= \sqrt{225-81} \)
\(\qquad \sf \dashrightarrow \: a= \sqrt{144} \)
\(\qquad \sf \dashrightarrow \: a= 12\: units\)
a sequence is given by the rule 4n^2
work out the 3rd term in the sequence
Answers
Answer: See below.
Step-by-step explanation:
See attachment. It depends on what is considered the "third" term. If n=2 then the result is 16. If 3, the result is 36.

Write down a quadratic equation in the form $x^2 + bx + c = 0$ whose solutions are $x = -7$ and $x = 1. $.
Answers
Answer:
an average weight of 10student was calculated to be 75. later it was discovered thatone weight wss insread as 35 instead of 50k.g. calculate the correct average weight
what is 3876153 x 46 =?????????
Answers
Answer:
178,303,038
Step-by-step explanation:
Multiply it
Or put it into a calculator
How can we determine whether the solution is a ray or a segment?
Answers
A ray has only one endpoint. A segment has two endpoints.
What is a line?
A line is an object in geometry that is infinitely long and has neither width nor depth nor curvature. Since lines can exist in two, three, or higher-dimensional spaces, they are one-dimensional objects. In everyday language, a line segment with two points designating its ends is also referred to as a "line."
A ray and a segment are parts of a line.
This line segment has two fixed-length endpoints, A and B. The distance between this line segment's endpoints A and B is its length.
In other words, a line segment is a section or element of a line with two endpoints. A line segment, in contrast to a line, has a known length.
A line segment's length can be calculated using either metric units like millimeters or centimeters or conventional units like feet or inches.
Ray has only one endpoint and the other ends go infinity.
To learn more about line segment, click on the below link:
https://brainly.com/question/11689511
#SPJ4
If (6 ki)² = 27-36i, the value of k is
Answers
Answer: k = √27-i
Step-by-step explanation: