what is the solution to the equation t-15=76
Answers
Answer:
T = 91
Step-by-step explanation:
Simplifying
T + -15 = 76
Reorder the terms:
-15 + T = 76
Solving
-15 + T = 76
Solving for variable 'T'.
Move all terms containing T to the left, all other terms to the right.
Add '15' to each side of the equation.
-15 + 15 + T = 76 + 15
Combine like terms: -15 + 15 = 0
0 + T = 76 + 15
T = 76 + 15
Combine like terms: 76 + 15 = 91
T = 91
Simplifying
T = 91
+15 +15
t=91
Related Questions
find the area of the polygon verticles of A(0,1)B(0,5)C(4,5) and D(6,1)
Answers
Answer:
20
Step-by-step explanation:
Draw that out on a coordinate grid, you get a trapezoid with one base 6 units long, one base 4 units long and a height of 4. Using the formula for area of a trapezoid
h(b1 + b2)/2
The height, 4, b1 is a base, 6, b2 is the other base, 4, we get
4(4+6)/2
40/2= 20
Please tell the answer
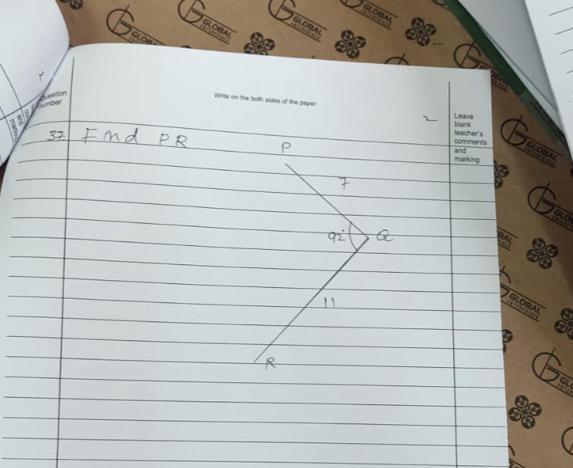
Answers
Answer:
18 Answer
Step-by-step explanation:
.: PQ +RQ
= 7+11
= 18
87) An object traveling in a straight line has position x(t) at time t. If the initial position is x(0)=2 and the velocity of the object is v(t)= (1+t^2)^1/3, what is the position of the object at time t=3
Answers
The position of the object at time t = 3 is approximately 6.59 units from the origin.
The velocity of an object is defined as the rate of change of its position with respect to time. Mathematically, we can express this as:
v(t) = dx/dt
where v(t) is the velocity of the object at time t, and dx/dt is the derivative of the position function x(t) with respect to time.
In this problem, we are given the velocity function v(t) as:
v(t) = (1+t²)¹/₃
To find the position function x(t), we need to integrate the velocity function with respect to time. We can do this as follows:
x(t) = ∫v(t)dt
x(t) = ∫(1+t²)^(1/3) dt
To evaluate this integral, we can use the substitution u = 1 + t², which gives du/dt = 2t. Substituting this into the integral, we get:
x(t) = (3/2) * ∫u¹/₃ * (1/2u) du
x(t) = (3/2) * ∫u⁻¹/₆ du
x(t) = (3/2) * (u⁵/₆ / (5/6)) + C
where C is the constant of integration.
To find the value of C, we need to use the initial condition x(0) = 2. Substituting t = 0 into the position function, we get:
x(0) = (3/2) * (u⁵/₆ / (5/6)) + C
x(0) = (3/2) * (1⁵/₆ / (5/6)) + C
x(0) = 2
Therefore, C = 2 - (3/2) * (1⁵/₆ / (5/6)) = 2 - (3/2) * (1 / (5/6)) = 2 - (9/5) = 1.2
Substituting C = 1.2 into the position function, we get:
x(t) = (3/2) * (u⁵/₆ / (5/6)) + 1.2
x(t) = (3/2) * ((1+t²)⁵/₆ / (5/6)) + 1.2
Finally, to find the position of the object at time t = 3, we simply substitute t = 3 into the position function:
x(3) = (3/2) * ((1+3²)⁵/₆/ (5/6)) + 1.2
x(3) ≈ 6.59
To know more about velocity here
https://brainly.com/question/17127206
#SPJ4
4) For the last ten years Joe has had his cholesterol count measured monthly, and his total cholesterol measures 180 with a standard deviation of 8. (FIX) Five months ago Joe added 1 monster a day to his diet and his last 5 cholesterol measurements were 171 , 165, 172, 168, 173 A) What is the probability of these 5 measurements 5 months in a row given his previous 10 years of measurements (hint, assume cholesterol measurements are normally distributed. You can calculate this using either a binomial framework (convert the 5 measurements to either 0 or 1 depending on a sensible rule, and calculate the probability of seeing that extreme a sample), or using the normal distribution, using the variance rules to calculate a standard deviation for the mean of the 5 measurements (assume standard deviation under monster is the same as before), and solving for the normal probability. These give different answers but both could be right) .(10 points) Statcrunch B) Suppose that on a monster, his average cholesterol is 170 with a standard deviation of 5. Also suppose that he switches to only using monsters for the summer months (June, July, August). Given that a particular cholesterol measurement in less than 172 what is the probability that it is summer
Answers
1) The probability of these 5 measurements 5 months in a row given Joe's previous 10 years of measurements is very low, approximately 0.0012.
A) The probability of each measurement being less than or equal to 171 is approximately 0.1587.
C) The probability that it is due to Joe using monsters during the summer months is approximately 0.205.
We can use a hypothesis test to determine the probability of these 5 measurements 5 months in a row given Joe's previous 10 years of measurements.
We will use a two-tailed z-test with a significance level of 0.05 to test the null hypothesis that Joe's cholesterol levels have not significantly changed after adding 1 monster a day to his diet. The alternative hypothesis is that his cholesterol levels have significantly decreased.
The test statistic is calculated as follows:
z = (X - μ) / σ
where , x is the mean of Joe's last 5 cholesterol measurements, μ is the mean of his cholesterol levels over the past 10 years, σ is the standard deviation of his cholesterol levels over the past 10 years (which is 8), and n is the number of measurements in the last 5 months (which is 5).
Substituting the values, we get:
z = {171 + 165 + 172 + 168 + 173} / {5} - 180 x {8/√10 × 12
z = -3.03
Using a standard normal distribution table, we find that the probability of getting a z-score of -3.03 or less is approximately 0.0012.
Since this is less than our chosen significance level of 0.05, we reject the null hypothesis and conclude that Joe's cholesterol levels have significantly decreased after adding 1 monster a day to his diet.
Therefore, the probability of these 5 measurements 5 months in a row given Joe's previous 10 years of measurements is very low, approximately 0.0012.
A) To calculate the probability of these 5 measurements 5 months in a row, we can assume that each measurement is a Bernoulli trial with a probability of success p of the cholesterol level being less than or equal to the normal level.
We can then use a binomial distribution to model the number of successful trials in 5 trials out of 10 x 12 = 120 trials.
Since Joe's normal cholesterol level is 180 with a standard deviation of 8, we can say that,
p = P(X < 171), where X is a normal random variable with mean 180 and standard deviation 8.
Using a standard normal distribution table or calculator, we can find that
P(X < 171) = 0.1587
Therefore, the probability of each measurement being less than or equal to 171 is approximately 0.1587. The probability of getting 5 measurements in a row less than or equal to 171 is then given by the binomial probability mass function:
P(X = 5) = {120 choose 5}(0.1587)⁵(1-0.1587)¹²⁰⁻⁵
= 0.00098
So the probability of getting 5 measurements in a row less than or equal to 171 is approximately 0.00098.
B) Given that a particular cholesterol measurement is less than 172, the probability that it is due to Joe using monsters during the summer months can be calculated using Bayes' theorem.
Let M be the event that Joe is using monsters during the summer months and C be the event that a particular cholesterol measurement is less than 172.
We want to find P(M | C), the probability that Joe is using monsters during the summer months given that the cholesterol measurement is less than 172.
Using Bayes' theorem, we have:
P(M | C) = {P(C | M)/P(M)} + P(C |- M)
P(- M)}
where P(C | M) is the probability of getting a cholesterol measurement less than 172 given that Joe is using monsters, P(- M) = 1-P(M) is the probability that Joe is not using monsters during the summer months, and P(C | - M) is the probability of getting a cholesterol measurement less than 172 given that Joe is not using monsters.
Using the information given in the problem, we have,
P(M) = 0.25,
P( M) = 0.75
P(C | M) = P(X < 171)
where , X is a normal random variable with mean 170 and standard deviation 5, and P(C | M) = P(X < 172),
where X is a normal random variable with mean 180 and standard deviation 8.
Using a standard normal distribution table or calculator, we can find that
P(X < 171) = 0.8413
P(X < 172) = 0.6306
Substituting these values into Bayes' theorem, we get:
P(M | C) = {(0.8413)/(0.25)} + (0.6306)/0.75)} = 0.205
Therefore, given that a particular cholesterol measurement is less than 172, the probability that it is due to Joe using monsters during the summer months is approximately 0.205.
Learn more about the probability visit:
https://brainly.com/question/13604758
#SPJ4
If the bottom row as a result of sythetic division is 1 3 0 4 0, then the quotient is which of the following? Select one:
Answers
The quotient of the synthetic division is x^3 + 3x^2 + 4
How to determine the quotient?The bottom row of synthetic division given as:
1 3 0 4 0
The last digit represents the remainder, while the other represents the quotient.
So, we have:
Quotient = 1 3 0 4
Introduce the variables
Quotient = 1x^3 + 3x^2 + 0x + 4
Evaluate
Quotient = x^3 + 3x^2 + 4
Hence, the quotient of the synthetic division is x^3 + 3x^2 + 4
Read more about synthetic division at:
https://brainly.com/question/18788426
#SPJ1
a hospital director is told that 56% of the treated patients are insured. the director wants to test the claim that the percentage of insured patients is below the expected percentage. a sample of 150 patients found that 75 were insured. find the value of the test statistic. round your answer to two decimal places.
Answers
The value of the test statistic is -1.5.
Test statistic:
A test statistic is a statistic used in statistical hypothesis testing. A hypothesis test is typically specified in terms of a test statistic, considered as a numerical summary of a data set that reduces the data to one value that can be used to perform the hypothesis test.
The formula for test statistic:
Test statistic = z = \(\frac{P - P_{0} }{\sqrt{\frac{P_{0( 1 -P_{0} } }{n} } }\)
A sample of patients n = 150
Patients insured =x = 75
P = x/n
= 75/ 150
= 1/2
= 0.5
\(P_{0}\) = 56/100
= 0.56
Putting the values we get:
z = \(\frac{0.5 - 0.56}{\sqrt{\frac{0.56( 1- 0.56)}{150} } }\)
= \(\frac{-0.06}{\sqrt{0.00164} }\)
= \(\frac{-0.06}{0.04}\)
= - 1.5
Therefore the test statistic is -1.5.
To know more about the test statistic refer to the link given below:
https://brainly.com/question/15110538
#SPJ4
Élizabeth a 20 ans de moins que son père. Si son père est trois fois plus âgé qu’elle, détermine l’âge de chacun.
Answers
Graph the exponential function.g(x) = (4/5)^xPlot five points on the graph of the function. Then click on the graph-a-function button.

Answers
ANSWER
EXPLANATION
We want to graph the given exponential function:
\(g(x)=(\frac{4}{5})^x\)To do this, we have to find 5 points that lie on the graph.
Let us solve the function for x = -6, -3, 0, 3, 6:
\(\begin{gathered} \Rightarrow x=-6: \\ g(-6)=(\frac{4}{5})^{-6}=3.81 \\ \Rightarrow x=-3: \\ g(-3)=(\frac{4}{5})^{-3}=1.95 \\ \Rightarrow x=0: \\ g(0)=(\frac{4}{5})^0=1 \\ \Rightarrow x=3: \\ g(3)=(\frac{4}{5})^3=0.51 \\ \Rightarrow x=6: \\ g(6)=(\frac{4}{5})^6=0.26 \end{gathered}\)Now, we have five points to plot the graph with:
\(\begin{gathered} (-6,3.81) \\ (-3,1.95) \\ (0,1) \\ (3,0.51) \\ (6,0.26) \end{gathered}\)Let us now plot the points and join the line:
That is the graph of the function

Alberto started out bench pressing 60 pounds. He then added 5 pounds every week. Determine whether the situation is linear or nonlinear, and proportional or nonproportional
Answers
Answer
linear
nonproportional
Step-by-step explanation:
Since for each equal change in time (1 week), there is an equal change in weight (5 lb), the situation is linear.
At time zero, the first week, the weight was not zero. It was 60 lb, so it is not proportional.
Answer:
linear
nonproportional
Ralph plans to sell a piece of property for 150,000. Is short-term note and 11% interest and long-term note for 9% interest. Find the amount of each note if the total annual paid it is 15,200
Answers
Answer:
Step-by-step explanation:
Short term 166,500 (150000x.11 then add that answer to 150000)
Long term 163,500
Help math problem help

Answers
Answer:
\(\frac{4}{5}\)
Step-by-step explanation:
sinA = \(\frac{opposite}{hypotenuse}\) = \(\frac{BC}{AC}\) = \(\frac{16}{20}\) = \(\frac{4}{5}\)
Help!! I need this now!! The instructions are on the top thank you!!

Answers
Answer:
LIVE TESTS NOT ALLOWED TO BE ANSWERED
Step-by-step explanation:
STOP THIS IS REPORTABLE
reverse the order of integration in the integral i = z 8 0 z x/2 0 f(x, y) dy dx , but make no attempt to evaluate either integral.
Answers
To reverse the order of integration in the integral i = z 8 0 z x/2 0 f(x, y) dy dx, we need to first draw the region of integration.
From the limits of integration, we see that the region is a right triangular pyramid with base in the xy-plane and height z.
To reverse the order of integration, we can integrate with respect to z first, and then with respect to x and y. Thus, the new integral becomes:
i = ∫0^8 ∫0^(2z) ∫0^x/2 f(x, y) dy dx dz
Note that we have reversed the limits of integration for x and z. This is because the limits of integration for x depend on the value of z. We have also kept the limit for y as it is since it is independent of z.
However, we have made no attempt to evaluate either integral, as requested in the question.
To know more about integration visit:
https://brainly.com/question/31744185
#SPJ11
A camera is able to capture 3/4 of a picture per second. How long will it take a camera to snap 6 pictures
Answers
The height of a cylinder is 7 inches. another cylinder with the same size base has double the volume. what is the height of the second cylinder? 3.5 in. 7 in. 14 in. 28 in.
Answers
Answer:
14
Step-by-step explanation:
Solve each equation mentally for x.
x • 7/3 = 1
Your answer must be in the form of a fraction.
Answers
determine whether the geometric series is convergent or divergent. (4 − 7 49 4 − 343 16 )
Answers
The common ratio 'r' is not constant, meaning that the series is not geometric.
Define the term geometric series?Each term in a geometric series is created by multiplying the previous term by a fixed constant known as the common ratio.
To determine if the geometric series (4, -7, 49, -343, 16) is convergent or divergent, we need to find the common ratio 'r' of the series.
r = (next term) / (current term)
r = (-7) / 4 = -1.75
r = 49 / (-7) = -7
r = (-343) / 49 = -7
r = 16 / (-343) = -0.0466...
We can see that the common ratio 'r' is not constant, meaning that the series is not geometric, and therefore we cannot determine if it is convergent or divergent.
To know more about divergent, visit:
https://brainly.com/question/15415793
#SPJ1
Which expression is equivalent to 6(4c + 5) + 7?
Answers
Answer:
24c+37
Step-by-step explanation:
If 2x -3y = 3 then find 16x 64y =?
Answers
Answer:
0 is the answer on 16 x 64y
Answer:
1 x = 4 y= 2/3 = 1. 66667 see attached and join the lines to create shaded area.
Step-by-step explanation:
2x -3y = 3
16x (64y) = ?
we can multiply the 2x by 8 to find x = 16 and -3y = -24y and 3 = 24
as shown 2nd one.
16x + (64y) = c
16x -24y = 24 = 64y - 24y = c
40y = c - 24
40y/24 = y
1.66667 = y
y = 1.6667 or 1 2/3
2x -3 ( 1 2/3 ) = 3
2x - 5 = 3
2x = 8
x = 4
y = 1. 66657


State if the three side lengths form an acute, obture, or right triangle 3 in 12 in and 13 in
Answers
Answer:
The triangle is obtuse.
Step-by-step explanation:
If a² + b² < c² , the triangle is obtuse.
If a² + b² = c² , the triangle is right triangle.
If a² + b² > c² , the triangle is acute.
~~~~~~~~~~~~~~~~
3, 12, 13
3² + 12² < 13²
9 + 144 < 169
153 < 169 ⇒ the triangle is obtuse.
I need help. Please help me!

Answers
Answer:
Step-by-step explanation:
omg are you in school do you have to go on the board bc you dead meat
Suppose you take 340 mg of a certain medication.
The amount of medication in your body decreases by 32% per hour.
Write a function for M(h), the number of milligrams of the medication in your body after h hours
Answers
Answer:
m= 340 × 0.68h
Step-by-step explanation:
Given that
You take 340 mg of the certain medication
And, the amount of medication would be reduced by 32% per hour
So we need to the find the function for M(h)
Here M denotes the milligrams
And, the h denotes the hours
So, the function would be
m = 340 × (1 - 0.32)h
m= 340 × 0.68h
The same would be considered and relevant
What is the slope-intercept form of the equation 2x+ y 10?
Answers
The slope-intercept form of the line equation 2x+ y = 10 is y = -2x + 10
There are three type of the equation of line:
- slope-intercept form.
The equation of line is: y = mx + b
Where:
m = slope
b = y-intercept
- point-slope form
The equation of line is: y - y₁ = m(x - x₁)
Where:
m = slope
(x₁,y₁) = a point on the line
- standard form
Ax + By + C = 0
Where A, B, C are constant
The given equation is: 2x+ y = 10
we will convert it into slope-intercept form y = mx + b
Subtract both sides by 2x:
2x+ y -2x = 10 -2x
y = -2x + 10
Hence, the slope-intercept form is y = -2x + 10
There was a typo in your question, most probably your question was:
What is the slope-intercept form of the equation 2x+ y = 10?
Learn more about line equation here:
https://brainly.com/question/28732353
#SPJ4
Which inequality matches the graph? -2x + 3y > 7 02x-3y
Answers
the inequality model. 5x-6y <0 is attached below.
What is inequality?
Inequalities are mathematical expressions where neither side is equal. In inequality, as opposed to equations, we compare two values. Less than (or less than or equal to), greater than (or greater than or equal to), or not equal to signs are used in place of the equal sign in between. Sometimes it can be about a "not equal to" relationship, where one thing is more than the other or less. In mathematics, an inequality is a relationship that results in a non-equal comparison between two numbers or other mathematical expressions.
2x + 3y > 7x-3y
5x-6y <0
So we have to plot this inequality.
Hence, the inequality model. 5x-6y <0 is attached below.
Learn more about inequality here:
brainly.com/question/14098842
#SPJ1

A pilot was scheduled to depart at 4:00 p.m., but due to air traffic, her departure has been delayed by 16 minutes. air traffic control approved a new flight plan that will allow her to arrive four times faster than she calculated in her original flight plan. let x represent the time, in minutes, of her original flight. create an equation that can be used to predict the number of minutes after 4:00 p.m. she will arrive at her destination.
a. y equals one fourth times x minus 16
b. y = 4x − 16
c. y equals one fourth times x plus 16
d. y = 4x 16
Answers
The equation that can be used to calculate how many minutes after 4:00 p.m. she will arrive at her location is y = 4x - 16.
The correct equation is:
y = 4x - 16
This equation represents the number of minutes after 4:00 p.m. the pilot will arrive at her destination. The variable x represents the time, in minutes, of her original flight, and y represents the number of minutes after 4:00 p.m. she will arrive at her destination. The expression "4x" represents the time the pilot will arrive at her destination if she had traveled at her original speed, and the "-16" represents the delay caused by air traffic.
To solve this equation, you would substitute the value of x into the equation and solve for y. For example, if the pilot's original flight time was 60 minutes, the equation would be:
y = 4(60) - 16
= 240 - 16
= 224
This means that the pilot will arrive 224 minutes after 4:00 p.m., or at 6:24 p.m.
To learn more about speed, refer:-
https://brainly.com/question/312131
#SPJ4
Anyone plz help me, plz show the working. THANK YOU SO MUCH!
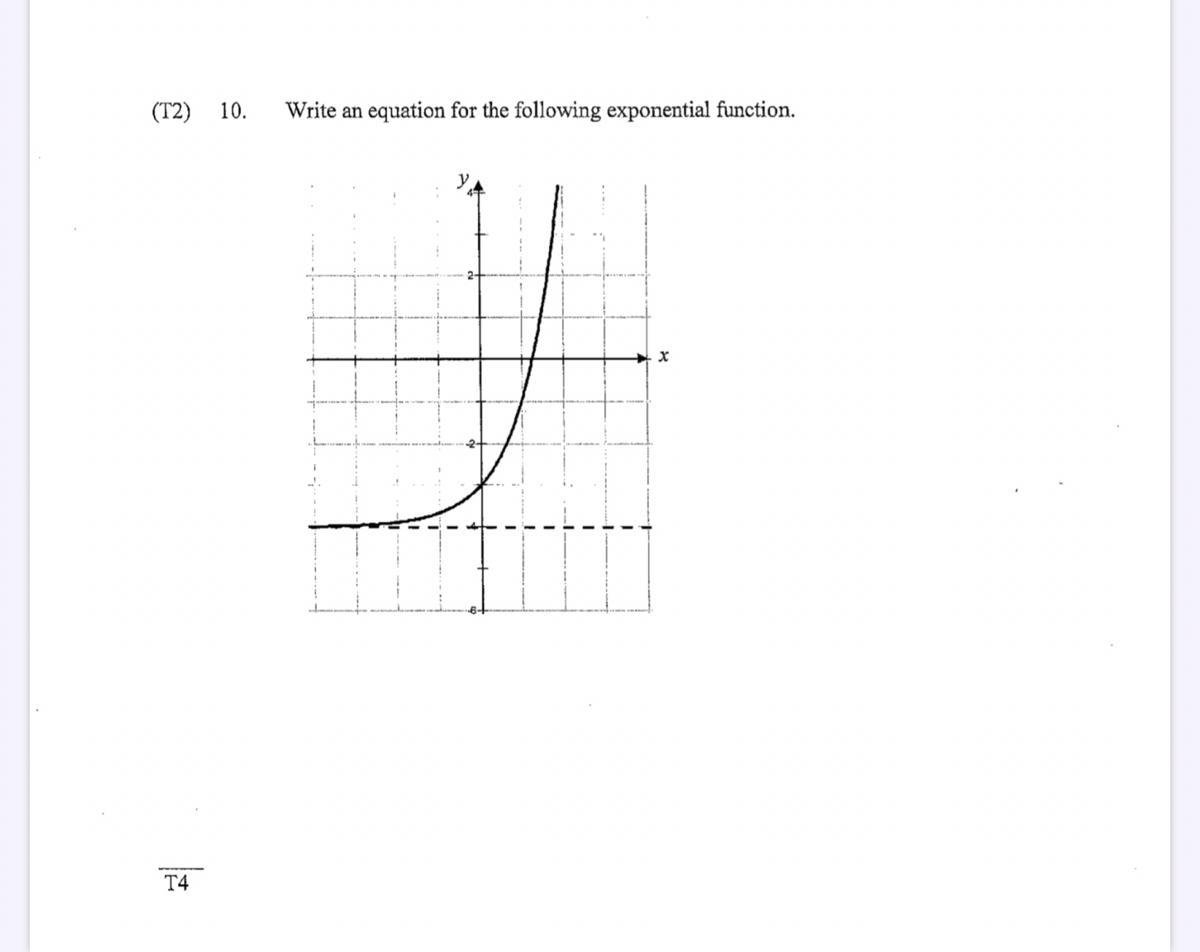
Answers
Please give me thanks and brainliest, this took lots of hard work and dedication
A tree grows three-fourth feet per year. How long will it take the tree to grow from
a height of 17 3/4 feet to a height of 25 1/2 feet?
Answers
Answer:
9 years
Step-by-step explanation:
37-21.25 =15.75ft
1.75ft per year
15.75 / 1.75 = 9 years
Which statement is not true about the line represented by the equation
PLZ HURRY
x + 2y = 14?
A,The slope is 1.
B.If x = 10, then y = 2
C.The y-intercept is (0, 7)
D. The x-intercept is (14, 0)
Answers
Answer:
A is false
Step-by-step explanation:
Can somebody please help me with this? Show work. It’s due today

Answers
Answer: The surface area of the rectangular box = the amount of wrapping paper needed to cover the rectangular box = 394.24 in.²
Step-by-step explanation:
Surface area = 2(wl + hl + hw).
Volume = Length x Width x Height
Given the following:
Volume = 476.16 in.³
Length = 4.8 in.
Width = 8 in.
Find the height (h) using the volume formula:
476.16 = 4.8 × 8 × h
476.16 = 38.4 × h
476.16/38.4 = h
h = 12.4 in.
Surface area = 2(wl + hl + hw) = 2(8 × 4.8 + 12.4 × 4.8 + 12.4 × 8) = 394.24 in.²
The amount of wrapping paper needed to cover the rectangular box = Surface area = 394.24 in.²
Pleaseeeeee help me with this!! And can you have answer in fraction form!?

Answers
Answer:
the answer is 24/5
.....