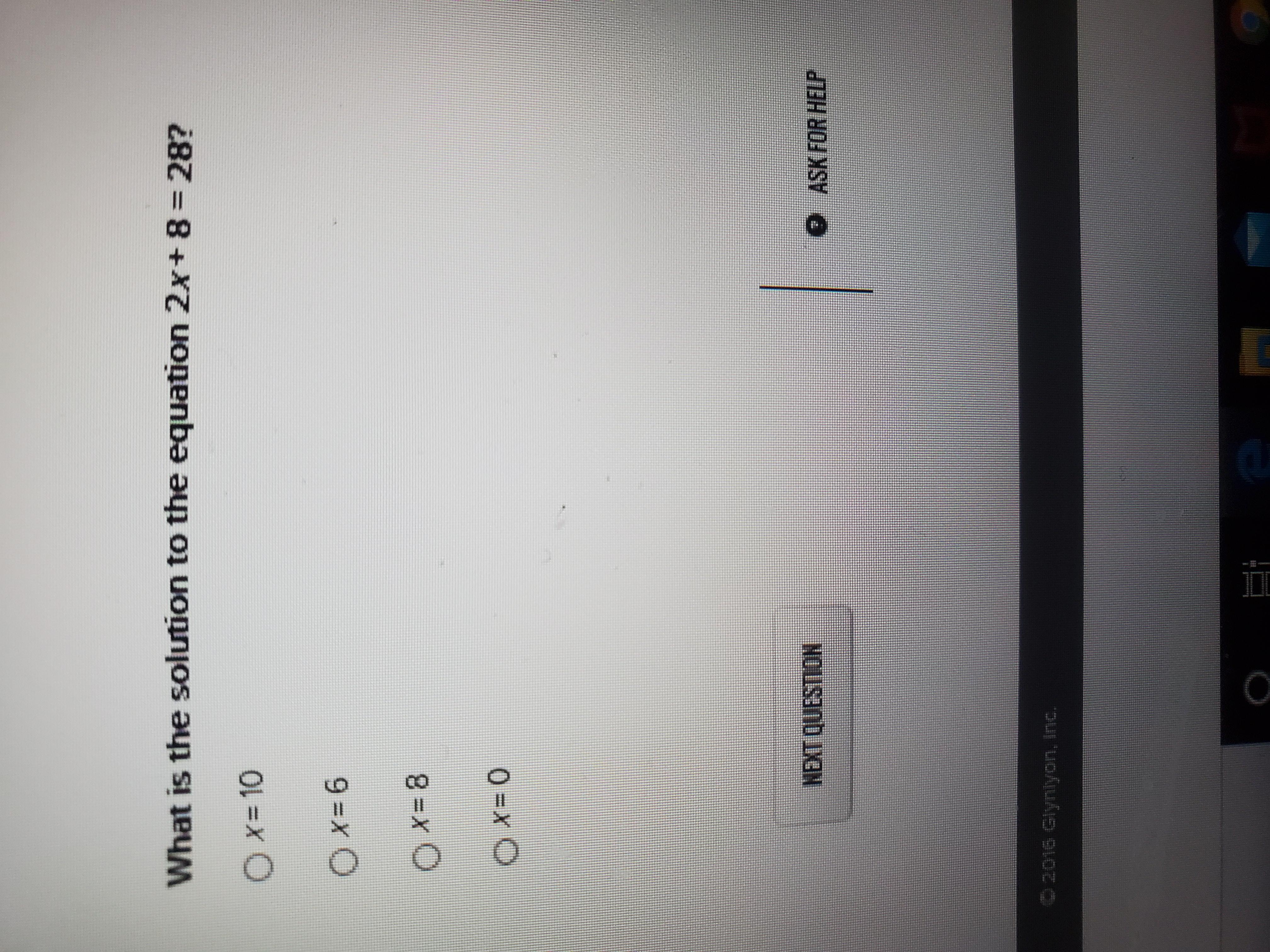
Answers
First we have to substract 8 from both terms. This way the 8 in the left term disappears:
\(\begin{gathered} 2x=28-8 \\ 2x=20 \end{gathered}\)And now we divide both terms by 2, so that in the left term we only have x:
\(x=\frac{20}{2}=10\)The answer is the first option, x = 10
Related Questions
Kelly has a rectangular fish aquarium that measures 18 inches long 8 inches wide and 12 inches tall what is the maximum amount of water the aquarium can hold?
Answers
Answer:
1728
Step-by-step explanation:
Volume=length*width*height
Vol=18*8*12=1728 cubic inches
On Monday, Erin ran a mile in 7.5 minutes. On Tuesday, she ran a mile in 6.9 minutes. What was the average time for a mile over those two days, expressed as a fraction?
Answers
Answer: 14.4/2
Step-by-step explanation: to find the average time, we add both numbers then divide by how many numbers we have, which is two. So 7.5 + 6.9 = 14.4. we then divide by 2, so 14.4/2.
5. What number is expressed in each of the models below? One flat represents 1 whole. One
rod represents 1 tenth, and one unit represents 1 hundredth. Write the number on the line.

Answers
Answer:
137 is the number expressed in each of the models.
One number is 7 less than a second number.Twice the second number is 2 less than 4 time the first
Answers
Andrew left his house at time zero and drove to the store, which is 10 blocks away, at a
speed of 5 blocks per minute. Then he stopped and went into the store for 2 minutes.
From there, he drove in the same direction at a speed of 5 blocks per minute until he
got to the bank, which is 10 blocks away from the store. He stopped at the bank for 3
minutes. Then he drove home at a speed of 4 blocks every minute. Make a graph of
showing the number of blocks away from home that Andrew is 2 minutes after he
leaves his house, until he gets back home.
Answers
the graph of Andrew's distance from home will look like this: Time (x-axis) 0 1 2 3 4 5 6 7 8 9 10 Distance (y-axis) 0 5 10 10 15 20 20 24 28 32 0
What is graph?Graph is a data structure which is used to represent relationships between objects or data points. It is composed of nodes and edges, where nodes are the objects and edges are the connections between the objects. Graphs are used to represent mathematical equations, networks, and data structures such as trees. They are also used to represent relationships between data points in large datasets. Graphs can be used to represent both directed and undirected relationships, and are commonly used in many fields including computer science, engineering, mathematics, and data science.
From the given information, we can create a graph that shows Andrew's distance from home as he drives to the store, to the bank, and back again. The x-axis will represent time (in minutes), and the y-axis will represent the number of blocks away from home.
At time zero, Andrew is at his home, so the graph will begin with a point at (0, 0). As he travels to the store, the graph will move up 5 blocks for every minute he drives. Therefore, after 2 minutes, he will be 10 blocks away from home, so the graph will be at (2, 10). After he stops at the store for 2 minutes, he will still be 10 blocks away from home, so the graph will stay at (2, 10).
When he leaves the store and drives to the bank, he will move 5 blocks each minute. After 5 minutes, he will be 25 blocks away from home, so the graph will be at (5, 25). After he stops at the bank for 3 minutes, he will still be 25 blocks away from home, so the graph will remain at (5, 25).
Finally, when he drives home, he will move 4 blocks for each minute he drives. After 5 more minutes, he will be back at his home, so the graph will be at (10, 0).
Therefore, the graph of Andrew's distance from home will look like this:
Time (x-axis) 0 1 2 3 4 5 6 7 8 9 10
Distance (y-axis) 0 5 10 10 15 20 20 24 28 32 0
To know more about graph click-
https://brainly.com/question/19040584
#SPJ1
Given the following information, find the equation in vertex form, factored form and standard form.
1. Vertex (1, 4) Point (2, -1)
Vertex form
Standard form
Answers
Answer:
Vertex:
\(f(x)=-5(x-1)^2+4\)
Standard:
\(f(x)=-5x^2+10x-1\)
Factored:
This is unfactorable.
Step-by-step explanation:
The parabola has a vertex at (1, 4) and it crosses a point at (2, -1).
We will start off with the vertex form, given by:
\(f(x)=a(x-h)^2+k\)
Where (h, k) is the vertex.
Therefore:
\(f(x)=a(x-1)^2+4\)
Since the function passes through (2, -1), f(x) = -1 when x = 2:
\(-1=a(2-1)^2+4\)
Solve for a:
\(-5=a(1)\Rightarrow a =-5\)
Therefore, vertex form is:
\(f(x)=-5(x-1)^2+4\)
To find the standard form, expand:
\(f(x)=-5(x^2-2x+1)+4\)
Distribute:
\(f(x)=-5x^2+10x-5+4\)
And simplify:
\(f(x)=-5x^2+10x-1\)
We can now factor. Which two values multiply to be 5 and add up to be 10?
Since this is no possible, the equation is unfactorable.
The cost of 5 kg of potatoes is £3.20
The cost of 0.5kg of carrots is 29p
Work out the total cost of 12 kg of potatoes and 1.5 kg of carrots.
Answers
Answer:
12kg=7.68
1.5=87
Step-by-step explanation:
I found the cost per kg
what ratio is equivilant to 4 : 5
Answers
Answer:
Any ratio where the original sides are both multiplied by the same number.
For example,
4 : 5 (your ratio)
4 x 2 : 5 x 2 (multiply both sides by a number)
8 : 10 (equivalent ration)
The area of the triangle below is 8.91 square inches. What is the length of the base?
2.2 in is the height will mark BRAINLIEST!!!!!!
Answers
2. A bank representative studies compound interest, so she can better serve customers. She
analyzes what happens when $2,000 earns interest several different ways at a rate of 2% for 3
years.
a. Find the interest if it is computed using simple interest.
$
LA
c. Find the interest if it is compounded continuously.
$
d. What is the difference in total interest if computed using simple interest or if compounded
continuously?
Answers
a) The interest if computed using simple interest for 3 years at 2% is $120.
c) The interest when compounded continuously for 3 years at 2% is $123.67.
d) The difference in total interest between using simple interest and continuously compounding is $3.67.
What is simple interest?Simple interest is a straightforward way of computing the interest paid on a loan.
The formula for calculating simple interest is P x R x T, where P = Principal, R = Rate, and T = Time.
The formula for continuous compounding first computes the future value (FV) from which the present value (PV) is deducted, as follows:
FV = PV x e ^ (i x t), where e is the mathematical constant approximated as 2.7183.
Principal = $2,000
Rate of interest = 2%
Period = 3 years
Simple Interest = $120 ($2,000 x 2% x 3)
Continuous compounding = FV - PV
FV = $2,000 x 2.7183 ^ (0.02 x 3)
= $2,000 x 1.06183697
= $2,123.67
Interest = $123.67 ($2,123.67 - $2,000)
The difference in total interest = $3.67 ($123.67 - $120)
Thus, continuous compounding produces a difference in the interest of $3.67 when compared to simple interest.
Learn more about compound interest and simple interest at brainly.com/question/3402162
#SPJ1
A square and a rhombus both have two sets of parallel sides.
Answers
Answer:
True
Step-by-step explanation:
Square and rhombus are actually from the family of parallelorgam and a parallelogram has 2 set of sides.
I hope im right!
n the figure below, m∠AED=88∘, m∠AEC=61∘, and m∠BEC=24∘. If m∠BED=x∘, then what is x?
Please and thank you!!

Answers
Check the picture below.
now, if we just add that shaded part of (x-24)° to the 61°, we'll end up with the whole AED angle or 88°.
\((x-24)~~ + ~~61~~ = ~~88\implies x+37=88\implies x=51\)

Practice polynomials
solve and show your work
3x^2-14x-5
Answers
Answer:
( − 5 ) ( 3 + 1 )
Step-by-step explanation:
Use the sum-product pattern: 3 2 − 1 4 − 5
3 2 + − 1 5 − 5
Common factor from the two pairs: 3 2 + − 1 5 − 5
( 3 + 1 ) − 5 ( 3 + 1 )
Rewrite in factored form
Answer:
Step-by-step explanation:
Standard form:
3x2 − 14x − 5 = 0
Factorization:
(x − 5)(3x + 1) = 0
Solutions based on factorization:
x − 5 = 0 ⇒ x1 = 5
3x + 1 = 0 ⇒ x2 = −1
3
≈ −0.333333
Extrema:
Min = (2.333333, −21.333333)
Answer:
(3 x + 1 ) ( x − 5 )
Which proportion can be used to show that the slope of JL is equal to the slope of MP
Answers
Answer:
See below and attached
Step-by-step explanation:
As per the graph we have:
Coordinates of JL are J(-7, 4), L(-4, 0)Coordinates of MP are M(-10, 8), P(-1, -4)Slope formula is:
m = (y₂ - y₁)/(x₂ - x₁)Slope of JL:
(0 - 4)/(-4-(-7)) = - 4 / 3Slope of MP:
(-4 -8)/(-1- (-10)) = -12 / 9 = - 4/3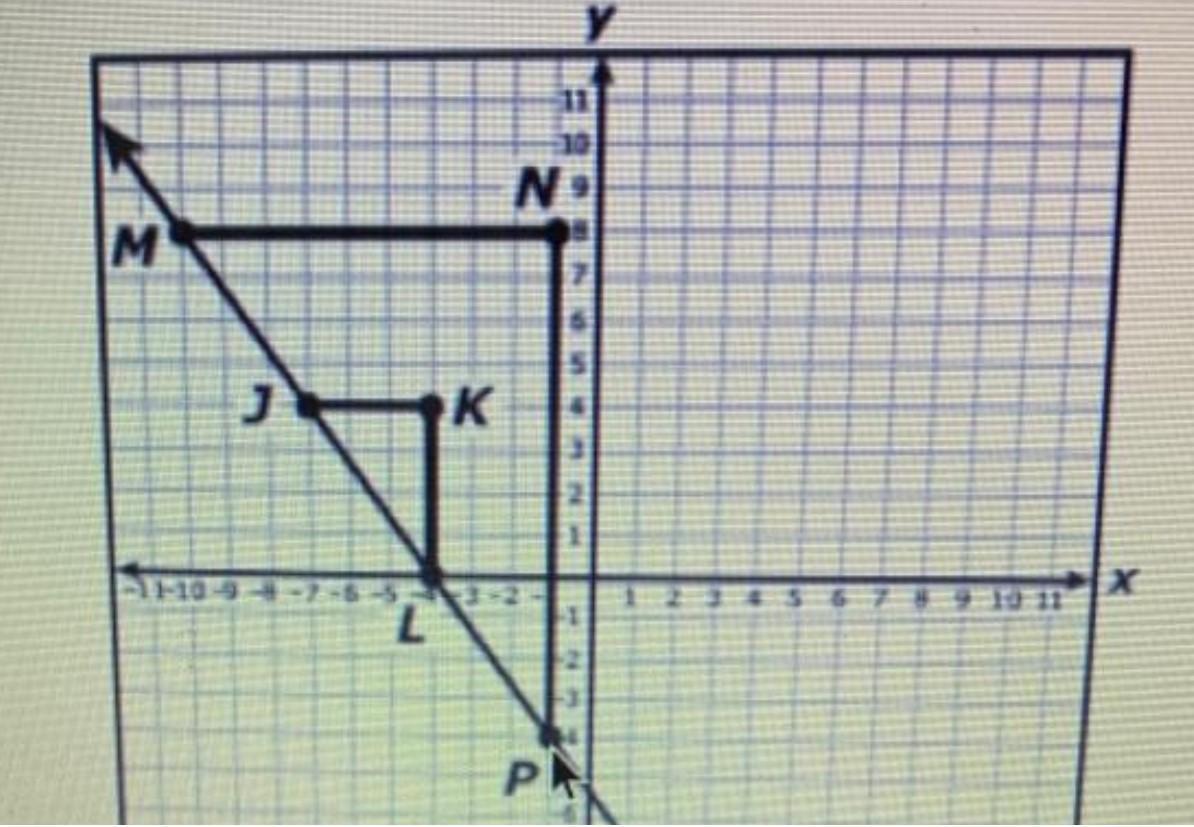
I need the area choices below

Answers
Answer:
Area of the shape is 244.98cm² is B
Step-by-step explanation:
Area of shape=Area of semi circle+Area of trapezoid
A=1/2 πr² + 1/2(a+b)h
A=1/2×3.142×7² + 1/2(14+18)10.5
A=1/2×3.142×49 + 1/2×32×10.5
A=76.98+168
A=76.98+168
A=244.98cm²
a study of the annual population of toads in a county park shows the population, S(t), can be represented by the function S(t) = 152(1.045)^t, where the t represents the number of years since the study started. based on the function, what is the growth rate?
Answers
Answer: 0.045 is the growth rate.
Step-by-step explanation:
A generic exponential growth function can be written as:
f(t) = A*(1 + r)^t
where A is the initial amount.
t is the unit of time.
r is the rate of growth.
For example if we have an increase of 10% per year, with an initial population of 100 we have that:
A = 100, r = 10%/100% = 0.10, t = number of years.
the equation will be:
f(t) = 100*(1 + 0.10)^t
Now, in this case the equation is:
S(t) = 152*(1.045)^t
We can write this as:
S(t) = 152*(1 + 0.045)^t
Then 152 is the initial amount and 0.045 is the growth rate.
Please look below (Please Explain and NO LINKS)

Answers
Answer:
Mean = Sum of all numbers divided by the amount of numbers
\(Mean/Average=\frac{3+1+1.5+1.25+2.25+4+1+2}{8} =\frac{16}{8} =2\)
Median = the middle number when the ordered from least to greatest.
From least to greatest: \(1, 1, 1.25, 1.5, 2, 2.25, 3, 4\)The two middle numbers are 1.5 and 2.If there are two middle numbers, find the mean/average of those numbers:
\(\frac{1.5+2}{2} =\frac{3.5}{2} =1.75\)
Therefore, the answer would be:
Mean = 2Median = 1.75
Which is correct ? ^^^^

Answers
Answer:
c
Step-by-step explanation:
C because your looking for y*48 which is 48y. It is c because (y*40)+(y*8) gives you 40y+8y which equals 48y.
Answer:
C.
Step-by-step explanation:
(y•40)+(y•8)
40y+8y
48y
48•y
PLEASE HELP I DONT GET THIS AND MY MOM IS MAD AT ME
A person is looking from a car to the top of a building. The angle of elevation to the top of the building from the car is 32°. The building is 200 feet away. How tall is the building? Round to the nearest foot.
Answers
Answer:
132.2 ft
Step-by-step explanation:
This is a right angle problem where 32 is the angle and 200 feet is the leg unederneath. To solve for the height we use tangent since we have the adjacent side and we are solving for the opposite side.
Steps:
1. tan32 = x/200
2. (tan32)200=x
3. x=132.2 ft
Tara took a total of 45 quizzes over the course of 9 weeks. After attending 10 weeks of school this quarter, how many quizzes will Tara have taken in total? Assume the relationship is directly proportional.
Answers
Answer:
After 10 weeks, Tara will have taken 50 quizzes.
Step-by-step explanation:
Given that Tara took a total of 45 quizzes during the 9-week course, to determine the number of quizzes she will take after 10 weeks, taking into account that it is a proportional relationship, the following calculation must be performed:
(45/9) x 10 = X
5 x 10 = X
50 = X
So, after 10 weeks, Tara will have taken 50 quizzes.
When a 3-D figure cut to create a cross-section parallel to the base which direction is the perpendicular vertical or horizontal 
Answers
Answer:
When a 3D figure is cut to create a cross-section parallel to the base, the direction of the perpendicular is vertical. This means that the cross-section will be perpendicular to the base and will have a vertical orientation.
A painter mixed 7 ounces of blue paint with every 11 ounces of yellow paint in order to make a green paint.
Problem:
Which ratio of ounces of blue paint to yellow paint will make the same shade of green paint?
Answers
Answer: 49:77
Step-by-step explanation:
In the month of September, all of the Kroger grocery stores in Nashville sold 429,382 eggs. In that same month, all of the Kroger grocery stores in Memphis sold 283,054 eggs. How many eggs did the Nashville and Memphis Kroger grocery stores sell all together in the month of September? Use 2 strategies to show how you found out how many eggs Kroger sold in September.
Answers
Answer:
712436 eggs were sold together
Step-by-step explanation:
429,382 + 283,054 = 712436
Please help if you can, this is due tomorrow.
In the diagram below, $\angle BAC=24^\circ$ and $AB=AC$.
If $\angle ABC=y^\circ$, what is the value of $y$?
[asy]
size(4.25cm);
pair a=(0,cos(pi/15)); pair b=(-sin(pi/15),0); pair c=-b; pair d=c+(1,0);
dot(a); dot(b); dot(c);
draw(c--a--b--c);
draw((2*a+3*b)/5-0.05*(cos(pi/15),-sin(pi/15))--(2*a+3*b)/5+0.05*(cos(pi/15),-sin(pi/15)));
draw((2*a+3*c)/5-0.05*(cos(pi/15),sin(pi/15))--(2*a+3*c)/5+0.05*(cos(pi/15),sin(pi/15)));
label(scale(0.75)*"$24^\circ$",a-(0,0.3),S);
label("$A$",a,N);
label("$B$",b,SSW);
label("$C$",c,S);
label(scale(0.85)*"$y^\circ$",b,NE);
[/asy]
Answers
The given diagram implies that the triangle $ABC$ is an isosceles triangle with angles of $24^\circ$. This can be verified by computing the length of the hypotenuse and using the Pythagorean Theorem.
What is equation?Equation is a mathematical expression that consists of variables, symbols, and numbers, and shows the relationship between different quantities. An equation can involve one or more unknowns, and can be represented as an equality or as an inequality. Solving an equation requires understanding the relationship between the different elements in the equation, and manipulating the equation to isolate the unknowns. Common types of equations include linear equations, quadratic equations, and polynomial equations.
From this diagram, we can conclude that $\angle ABC$ is an isosceles triangle. This is because the angles opposite equal sides of a triangle must be equal. Since $\angle BAC=24^\circ$, $\angle ABC$ must be $24^\circ$. Furthermore, the sides $AB$ and $AC$ are equal, so $ABC$ is an isosceles triangle.
This conclusion can be verified by using the Pythagorean Theorem. If $AB=AC$, then it follows that $BC = \sqrt{AB^2 + AC^2} = \sqrt{2AB^2}$. Since $AB=3$, it follows that $BC=\sqrt{2*3^2}=6$. Therefore, the triangle $ABC$ is a right triangle with legs of length 3 and hypotenuse of length 6. Since $\angle BAC = 24^\circ$, it follows that $\angle ABC = 24^\circ$, verifying that the triangle is isosceles.
In conclusion, the given diagram implies that the triangle $ABC$ is an isosceles triangle with angles of $24^\circ$. This can be verified by computing the length of the hypotenuse and using the Pythagorean Theorem.
To know more about equation click-
http://brainly.com/question/2972832
#SPJ1
Answer:
78
Step-by-step explanation:
1. In 2020, the populations of City A and City B were equal. From 2015 to 2020, the population of City A increased by 20% and the population of City B decreased by 10%. If the population of City A was 120,000 in 2015, what is the population of City B in 2015?
2. A chef is preparing a sauce for a steak she offers as a key dish in her menu. To prepare the sauce she needs to prepare a mix with 40% butter, with the rest being egg yolk. In the kitchen right now, she only has a sauce that has 20% butter (rest is egg yolk) and a sauce that has 50% butter (rest is egg yolk) in stock. In what ratio should she mix the 20% sauce with the 50% sauce in order to obtain the 40% sauce that she needs to prepare her famous recipe?
3. A book was on sale for 30% off its original price. If the sale price of the book was $28, what was the original price of the book? (Assuming there is no sales tax)
4. At a retail store, they needed to do surveys of 32 stores which equals 40% of all their stores. How many stores does the retailer have in total?*
Answers
Answer:
180000 people
1 : 2
$40
80 stores
Step-by-step explanation:
1.)
Population in 2020 are equal : Let population =
City A increased by 20% From 120,000 in 2015
(1 + 0.2) * 120,000 = (1.2 * 120,000) = 144,000
Hence, city A = 144,000.
Since, city A and B have equal population ; city B also has a population of 144000 in 2020.
Let population in 2015 = x
(1 - 0.2) * x = 144000
0.8x = 144000
x = 144000/0.8
x = 180,000
2.)
Let proportion of 20% butter = x and proportion of 50% butter = 1 - x
0.2x + 0.5(1 - x) = 0.4
0.2x + 0.5 - 0.5x = 0.4
-0.3x + 0.5 = 0.4
-0.3x = 0.4 - 0.5
-0.3x = - 0.1
x = 0.1/0.3
x = 0.3333
(1-x) = 1 - 0.33333 = 0.6666%
0.3333% of 20% butter
0.6666% of 50% butter
Hence ;
0.3333 : 0.6666
1 : 2
3.)
Let original price of book = x
Discount on sale = 30%
Sale price = $28
Sale price = original price * (1 - discount)
$28 = (1 - 0.3) * x
$28 = 0.7x
x = $28/0.7
x = $40
4.)
Let total number of stores = x
Store surveys needed = 32
40% of total stores = 32 stores
0.4x = 32
x = 32 / 0.4
x = 80
Set of whole numbers from 1 to 10 inclusive greater than seven and odd
Answers
Answer:
{7, 9}
(Numbers from 1 to 10 equal to or greater than 7 are 7 and 9)
Step-by-step explanation:
We have to find the set of whole number greater than and equal to 7 from 1 to 10,
Now, From 1 to 10, the odd numbers are, 1,3,5,7,9,
And of these, 7 and 9 are equal to or greater than 7
So, we get the set,
{7, 9}
Elisa withdrew $24 at a time from her bank account and withdrew a total of $192. Frances withdrew $46
at a time from his bank account and withdrew a total of $230. Who made the greater number of
withdrawals?
withdrawals, while
(seleled made the greater number of withdrawals, because she made
(select) only made withdrawals.
Answers
Answer: Elisa
Step-by-step explanation: the first one did 8 withdraws the second one did 5 withdraws
(divide the total by the amount withdrawn each time)
Answer:
Elisa made more because she made 8 and Frances only made 5
Step-by-step explanation:
192/24= 8
230 / 46 = 5
Part AGiven f (x) = -x + 1 and g(x) = 2x - x, find [fºg)(x) and (sf(x). State the domain and range for each.Find [f.g] (x) and (gof)(x).Drag the expressions to the correct bins to define each function.[fogl(x)[g • f](x)-21' to+ 121 - 21+1-21 -+1-21 -+221²-51+ 2- 21+ + 21+--21 +6r²-51+1

Answers
f°g(x) = f(g(x))
To fid it we need to replace x = g(x) into f(x) as follows:
\(\begin{gathered} f(x)=-x+1 \\ f(g(x))=-(2x^3-x)+1 \\ f\circ g(x)=-2x^3+x+1 \end{gathered}\)Since the obtained function is a polynomial, its domain and range are all real numbers.
g°f(x) = g(f(x))
To fid it we need to replace x = f(x) into g(x) as follows:
\(\begin{gathered} g(x)=2x^3-x \\ g(f(x))=2(-x+1)^3-(-x+1) \\ g\circ f(x)=2\lbrack(-x)^3+3\cdot(-x)^2\cdot1+3\cdot(-x)\cdot1^2+1^3\text{\rbrack+x}-1 \\ g\circ f(x)=2\lbrack-x^3+3x^2-3x+1^{}\text{\rbrack+x}-1 \\ g\circ f(x)=-2x^3+6x^2-6x+2\text{+x}-1 \\ g\circ f(x)=-2x^3+6x^2-5x+1 \end{gathered}\)Since the obtained function is a polynomial, its domain and range are all real numbers.
Why 6:4 and 18:8 are not equivalent ratios?
Answers
The simplest form of the ratios are not the same, hence, the ratios 6:4 and 18:8 are not equivalent ratios
In order to show why the given ratios are not equivalent ratios, we need to express them in their simplest form as shown:
For the ratio of 6:4
6:4 = 6/4
simplify.
= 3/2
= 3×2/2×2
= 3/2
= 3:2
For the ratio of 18:8
18:8 = 18/8
simplify.
= 9/4
= 9×2/4×2
= 9/4
= 9:4
Since the simplest form of the ratios are not the same, hence, the ratios 6:4 and 18:8 are not equivalent ratios.
Learn more about Ratio and Proportion here:
brainly.com/question/3796978
#SPJ9
The prime factorization of a number is 2 with a small 3 at the top x9 explain why this is correct or incorrect?