What is the slope of any line parallel to the line 2x+3y=11?
1. - 2/3
2. 2/3
3. 2
4. - 2
Answers
Hope this helps
Have a great day/night
Feel free to ask any questions
Related Questions
a 35 foot ladder leans against the top of a building. the ladder's base is 9.7 feet from the building. find the angle of elevation between the ladder and the ground.
Answers
As a result, there is a about 74.53 degree elevation difference between the ladder and the ground.
what is angle ?A geometric shape known as an angle is created when two rays or line segments come together at a location known as the vertex. The sides of the angle are the rays or line segments. Angles are used to define the amount of rotation or inclination between two lines or planes and are commonly measured in degrees or radians. The most popular unit of measurement for angles is the degree, which is derived from the 360 equal divisions of a circle. Angles are measured in degrees using a protractor, and each component is referred to as a degree.
given
We may resolve this issue using trigonometric functions. The elevation angle between the ladder and the ground will be denoted by the symbol. Next, we have
opposite/hypotenuse of sin()
adjacent/hypotenuse = cos()
The building's height in this instance serves as the opposing side, and the length of the ladder serves as the hypotenuse. We thus have:
height/35 cos() = 9.7/35 sin()
By rearranging the first equation, we can find the height:
height equals 35*sin()
The second equation can then be changed to include the following expression:
cos(θ) = 9.7/35
cos(θ) = 0.2771
By taking the inverse cosine of both sides, we can now solve for :
θ = cos^(-1)(0.2771) (0.2771)
7.453 degrees
As a result, there is a about 74.53 degree elevation difference between the ladder and the ground.
To know more about angles visit:
https://brainly.com/question/14569348
#SPJ1
A cell phone company charges by the minute (and partial minute) for making phone calls. Arionna’s plan includes 300 minutes in the $20 monthly base cost. If she uses more than 300 minutes in a month, there is a $5 overage fee and an additional charge of $0.25 per minute. Which graph represents the monthly cost, y, in dollars for making x minutes of calls?
Answers
Answer:
The cell phone charges is an illustration of a piecewise function represented as: y = 20; x <=300 and y = 0.25x- 50; x > 300
How to draw the graph?
When the number of minutes is not more than 300 minutes, the charge is:
y = 20; x <=300
When it is above 300, the function is:
y = 20 + 5 + (x - 300) * 0.25
Open the bracket
y = 20 + 5 + 0.25x - 75
Evaluate the sum
y = 0.25x- 50
So, the piecewise function is:
y = 20; x <=300
y = 0.25x- 50; x > 300
Step-by-step explanation:
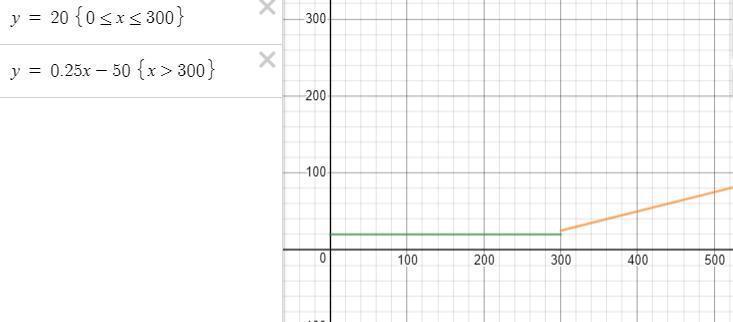
The graph that represents the monthly cost, y, in dollars for making x minutes of calls is:
In the graph,
The line starts at y = 20 for x = 0 and then becomes a straight line with a slope of 0.25 for x > 300.
What is inequality?It shows a relationship between two numbers or two expressions.
There are commonly used four inequalities:
Less than = <
Greater than = >
Less than and equal = ≤
Greater than and equal = ≥
We have,
To graph the monthly cost, we need to consider two cases:
Case 1: If x ≤ 300, then the monthly cost is a constant $20.
Case 2: If x > 300, then the monthly cost is a linear function of x:
Now,
y = 20 + 5 + 0.25(x - 300) = 25 + 0.25x - 75
y = 0.25x - 50
Therefore,
We can graph the monthly cost as follows:
For x ≤ 300, the graph is a horizontal line at y = 20.
For x > 300, the graph is a line with a slope of 0.25 and y-intercept -50.
Thus,
In the graph,
The line starts at y = 20 for x = 0 and then becomes a straight line with a slope of 0.25 for x > 300.
Learn more about inequalities here:
https://brainly.com/question/20383699
#SPJ5
6. Consider an urn which contains red balls and green balls. Initially there is just one green ball and one red ball in the urn. At each time step a ball is chosen randomly from the urn: (i) If the ball is red, then it's returned to the urn with an additional red ball; (ii) if the ball is green, then it's returned to the urn with an additional green ball. Let Xn denote the number of red balls in the urn after n draws. Suppose after 100 draws, there are 70 red balls, that is X100 = 70. What is the expected number of red balls in the urn after another 100 draws, that is E[X200|X100 = 70]? Round your answer to the nearest integer. Hint: consider Yn = Xn/(n + 2)
Answers
Rounding to the nearest integer, we have E[X200|X100 = 70] ≈ 92 for the urn.
The expected number of red balls in the urn after another 100 draws, denoted by E[X200|X100 = 70], can be found using the formula:
E[X200|X100 = 70] = E[Y200|Y100 = 35/51] * (200 + 2) - 2
where Yn = Xn/(n + 2).
Since Yn is a random variable, we need to find its expected value at time 200 given that it was 35/51 at time 100. Using the fact that Yn = Xn/(n + 2), we have:
E[Y200|Y100 = 35/51] = E[X200/(200 + 2)|X100/(100 + 2) = 35/51]
= (200/102) * E[X200|X100 = 70]
where we used the fact that E[aX] = aE[X] for any constant a.
Now, since we know X100 = 70, we can use the fact that Xn follows a binomial distribution with parameters n and p, where n is the number of draws and p is the probability of drawing a red ball. At time 100, we have made 100 draws and obtained 70 red balls, so the probability of drawing a red ball at time 100 is p = 70/100 = 7/10. Therefore, we have:
E[X200|X100 = 70] = E[X200/(200 + 2)|X100/(100 + 2) = 35/51]
= (200/102) * E[X200|X100 = 70]
= (200/102) * (100 + 2) * (7/10)
= 92
Rounding to the nearest integer, we have E[X200|X100 = 70] ≈ 92.
Learn more about urn here:
https://brainly.com/question/30666719
#SPJ11
will give brainliest to the person who solves all 3 :)

Answers
I need this answered its due soon

Answers
A is false because this graph doesn't have any relative minimums because it never increases
B is false because this graph never increases
C is true
D is true because the graph never goes below 3, but it's blurry so I might be wrong
E is true because it never stops decreasing and has a domain of all real numbers
halp me plss halp me

Answers
Answer:
a^2+b^2=c^2
Step-by-step explanation:
c is the x the side u want to find. usually a and b is given to you
also ^2 this means squared
i need hep filling in the table using the function rule. please please please fast

Answers
Answer:
qreg
Step-by-step explanation:
ergreg
Item 4
Solve the equation.
23h−13h+11=8
h=
Answers
What is one formula containing pi that would be useful in life. This could be any type of formula: circumference, area, volume,
Answers
Answer:
Area of semi-circle = \(\frac{1}{2}\pi r^{2}\)
Perimeter of semi-circle = \(\pi r + 2r\) where r is the radius
Step-by-step explanation:
Pi has been used in the construction of arches, bridges, churches and buildings.
Since the bridges and arches are semicircles, Pi helps in determining perimeter of the semicircle which in turn helps in calculating the amount of material required for construction.
Area of semi-circle = \(\frac{1}{2}\pi r^{2}\)
Perimeter of semi-circle = \(\pi r + 2r\) where r is the radius
Diagonals of a parallelogram measure16cm and 14cm
respectively. The shorter side measures 10cm
. Find the longer side.
Answers
Diagonals of a parallelogram measure 16cm and 14cm respectively. The shorter side measures 10cm. The longer side of the parallelogram measures 2 * sqrt(13) cm.
To find the length of the longer side of the parallelogram, we can use the properties of parallelograms. In a parallelogram, opposite sides are equal in length.
Let's assume that the longer side of the parallelogram measures x cm. Since the shorter side is given as 10 cm, we have two sides of the parallelogram: 10 cm and x cm.
We are also given the lengths of the diagonals, which are 16 cm and 14 cm. In a parallelogram, the diagonals bisect each other. This means that the diagonal divides the parallelogram into two congruent triangles.
Using the properties of these triangles, we can apply the Pythagorean theorem. The diagonals, shorter side, and longer side of the parallelogram form a right triangle.
Using the Pythagorean theorem, we can set up the following equation:
(14/2)^2 + (16/2)^2 = 10^2 + (x/2)^2
Simplifying the equation, we have:
49 + 64 = 100 + (x/2)^2
113 = 100 + (x/2)^2
(x/2)^2 = 13
x/2 = sqrt(13)
x = 2 * sqrt(13)
Learn more about Pythagorean theorem here:
https://brainly.com/question/14930619
#SPJ11
A standard fair dice is rolled twice. What is the probability of getting an even number on the first roll and any number except 5 on the other?
Answers
Answer:
Step-by-step:
Well, the probability for getting an even number on the first roll is 1/2
The probability for getting not 5 would be 5/6
You can make a tree diagram.
1 2 3 4 5 6
1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6
The numbers on the top represent the first roll. The numbers on the bottom represent the second roll. The first roll should be an even number, so we know that we should be looking at the even numbers. The second one should be anything but 5. So, what I did was look at the numbers that weren't 5. Look at the diagram with the even number at the top. then, look at the numbers that aren't 5 below. Since there are 5 numbers that aren't 5, and 3 even numbers, multiply 3 x 5 and you'll have 15. So add all the numbers at the bottom and that would be 36, so it's 15/36.
If p^2-n^2=1 prove that :
(x^m* x^n )^m-n* (x^p*x^-n)^n+p * (x^p*x^-m)^p+m = x^2
Answers
Let's begin by simplifying each of the terms in the expression on the left-hand side of the equation:
(x^m * x^n)^(m-n) = x^(m-n)*(m-n)
(x^p * x^(-n))^(n+p) = x^(n+p)*(p-n)
(x^p * x^(-m))^(p+m) = x^(p+m)*(p-m)
Now, let's substitute the given equation p^2 - n^2 = 1 into these expressions:
x^(m-n)*(p^2-n^2) = x^(m-n)
x^(n+p)*(p^2-n^2) = x^(n+p)
x^(p+m)*(p^2-n^2) = x^(p+m)
Simplifying each of these expressions using the given equation, we get:
x^(m-n) = x^(m-n)
x^(n+p) = x^(n+p)
x^(p+m) = x^(p+m)
Therefore, the left-hand side of the equation simplifies to:
x^(m-n) * x^(n+p) * x^(p+m) = x^(m-n + n+p + p+m) = x^(2m) = x^2^(m-n + n+p + p+m)
Thus, we have proved that:
(x^m * x^n)^(m-n) * (x^p * x^(-n))^(n+p) * (x^p * x^(-m))^(p+m) = x^2
which is the same as the given equation.
16
16
С
12
2x + 34
I’m not sure how to solve it

Answers
Answer:
x = 13---------------------------------
Connect the center with the point of tangency.
It will make a right triangle with legs 16 and 12.
Use Pythagorean theorem to set up an equation, then solve it for x.
The hypotenuse of the triangle is:
-2x + 34 + 12 = - 2x + 46It needs to be a positive length, so:
-2x + 46 > 0 ⇒ 46 > 2x ⇒ 23 > x ⇒ x < 23The equation:
(-2x + 46)² = 16² + 12²4(-x + 23)² = 4(8²) + 4(6²)(-x + 23)² = 8² + 6²(-x + 23)² = 100(-x + 23)² = 10²- x + 23 = ± 10x = 13 or x = 33The second root (x = 33) is discarded as greater than 23, so the answer is x = 13.
i need help does anyone know this question

Answers
Answer:
The third answer is correct.
Step-by-step explanation:
You are going to translate the smaller quadrilateral (4 sided figure) to the larger quadrilateral. Then you need the scale factor from the smaller figure to the larger.
Side EF times the scale factor will give you side AB. Let's call the scale factor s then our equation would be:
EF x s = AB To find s divide both sides by EF
\(\frac{EF(s)}{EF}\) = \(\frac{AB}{EF}\)
s = \(\frac{AB}{EF}\) This is our scale factor.
Helping in the name of Jesus.
A roulette wheel consists of 38 slots, numbered 0, 00, 1, 2,. , 36. To play the game, a metal ball is spun around the wheel and allowed to fall into one of the numbered slots. The slots numbered 0 and 00 are green, the odd numbers are red, and the even numbers are black. (a) Determine the probability that the metal ball falls into a green slot. Interpret this probability. (b) Determine the probability that the metal ball falls into a green or a red slot. Interpret this probability. (c) Determine the probability that the metal ball falls into 00 or a red slot. Interpret this probability (d) Determine the probability that the metal ball falls into the number 31 and a black slot simultaneously. What term is used to describe this event? (a) P(green) = ___ (Type an integer or decimal rounded to four decimal places as needed. ) If the wheel is spun 100 times, one would expect about __ spin(s) to end with the ball in a green slot. (Round to the nearest integer as needed. ) (b) P(green or red) = ___
(Type an integer or decimal rounded to four decimal places as needed. ) If the wheel is spun 100 times, one would expect about __ spin(s) to end with the ball in either a green or red slot. (Round to the nearest integer as needed. ) (c) P(00 or red)= ___ (Type an integer or decimal rounded to four decimal places as needed. )
Answers
(a). There is a 5.26% chance that the metal ball falls into a green slot.
(b). There is a 52.63% chance that the metal ball falls into either a green or a red slot on any given spin of the roulette wheel.
(c). P(00 or red) ≈ 0.5263
(d). This event is called impossible.
(a) P(green) = 2/38 = 1/19 ≈ 0.0526.
This means that there is a 5.26% chance that the metal ball falls into a green slot on any given spin of the roulette wheel.
If the wheel is spun 100 times, one would expect about 5 spins to end with the ball in a green slot. (Expected value = 100 x P(green) = 100/19 ≈ 5.26, which we round to the nearest integer.)
(b) P(green or red) = P(green) + P(red) = 2/38 + 18/38 = 20/38 ≈ 0.5263. This means that there is a 52.63% chance that the metal ball falls into either a green or a red slot on any given spin of the roulette wheel.
If the wheel is spun 100 times, one would expect about 53 spins to end with the ball in either a green or red slot. (Expected value = 100 * P(green or red) = 2000/38 ≈ 52.63, which we round to the nearest integer.)
(c) P(00 or red) = P(00) + P(red) = 2/38 + 18/38 = 20/38 ≈ 0.5263. This means that there is a 52.63% chance that the metal ball falls into either 00 or a red slot on any given spin of the roulette wheel.
(d) The probability that the metal ball falls into the number 31 and a black slot simultaneously is zero, since 31 is an odd number and all odd numbers are red on the roulette wheel. This event is called impossible.
To learn more about the probability;
brainly.com/question/11234923
#SPJ1
When you add a positive number and a negative number, how can you tell whether the sum will be positive or negative? (7th grade)
Answers
Howdy! My name is Christian and I’ll try and help you with this question!
Date: 9/29/20 Time: 9:11 am CST
Answer:
When the posiotive varibale is greater then the negative, the answer will be positive, when the negative variable is greater than the positive, the answer will be negative.
Explanation:
When adding a positive and a negative it could be either positve or negative ouput. If you had -50 and you added +60 the ouput is 10.
But if you had +50 and you added -60 the output would be -10.
Hope this helps you with your question!
Sincerely,
Christian
Someone please help me

Answers
=========================================================
Explanation:
Take away the four white small squares on the left side. To balance things out, you have to add 4 black squares to the right side.
Also, take away the two white long rectangles from the right side. To balance this out, you have to add 2 gray long rectangles to the left side.
You should have:
5 gray rectangles, and no squares (of any color) on the left side10 black squares, no long rectangles (of any color), on the right sideFrom here you'll group up the 10 black squares so that you'll have 2 black squares per gray rectangle.
This means the solution is 2.
-------------------------------------
If you're curious about the algebraic way to solve, then you could do this:
3x-4 = -2x+6
3x+2x = 6+4
5x = 10
x = 10/5
x = 2
This method doesn't require us to use the visual model.
In triangle ABC, AC=13, BC=84, and AB=85. Find the measure of angle C
Answers
Answer:
90°
Step-by-step explanation:
Angle C = arccos((84²+13²-85²)/(2×84×13))
= arccos(0/2184)
= arccos(0)
= 90°
Answered by GAUTHMATH
advance tickets for a school play went on sale. the price of each student ticket was $4 and everyone else paid $5. on the first day, no more than $80 in tickets were sold. describe and explain the possible values of s, the number of student tickets sold, and e, the number of tickets sold to non student’s.
Answers
Answer:
0student 16non-student,
5student 12non-student,
10student 8non-student,
15student 4non-student,
20student 0non-student
Step-by-step explanation:
s student tickets, e non student
4s + 5e = 80
s e
0 16 4(0) + 5(16) = 80
5 12 4(5) + 5(12) = 80
10 8 4(10) + 5(8) = 80
15 4 4(15) + 5(4) = 80
20 0 4(20) + 5(0) = 80
What is the Domain for
{(2,0),(5,-2),(6,-5),(7,3),(3,1)}
Answers
Answer:
domain { 2, 3, 5, 6, 7 }
Step-by-step explanation:
the domain is the x- coordinates of the given ordered pairs, that is
domain { 2, 3, 5, 6, 7 }
A rectangular table that is placed lengthwise against a wall is 8 feet long
and 4 feet wide. Balloons will be attached 8 inches apart along the three
exposed sides, with one balloon at each of the four corners. How many balloons are needed?
Answers
Considering the perimeter of the rectangular table, it is found that 36 ballons are needed.
What is the perimeter of a rectangle?The perimeter of a rectangle of length l and width w is given by:
P = 2(l + w).
In this problem, the dimensions of the table are l = 8 ft and w = 4 ft, hence the perimeter is of:
P = 2(l + w) = 2 x 12 = 24 ft.
Ballons will be attached 8 inches = 2/3 feet along the perimeter, hence the number of ballons needed is given by:
\(n = \frac{24}{\frac{2}{3}} = 36\)
More can be learned about the perimeter of a rectangle at https://brainly.com/question/10489198
Kristian buys a meal for $8.40 calculate the fraction of the $72 after buying the computer game which costed $32.40 and the meal. give ur answer in its lowest terms
Answers
Answer:
After buying the meal and the computer game, Kristian has 43.33% of his money left.
Step-by-step explanation:
Given that Kristian buys a meal for $ 8.40, to calculate the fraction of the $ 72 after buying the computer game which cost $ 32.40 and the meal, the following calculation must be performed:
72 = 100
8.40 + 32.40 = X
72 = 100
40.80 = X
40.80 x 100/72 = X
4,080 / 72 = X
56.66 = X
100 - 56.66 = 43,333
Therefore, after buying the meal and the computer game, Kristian has 43.33% of his money left.
b. Isabella has a second tray that has a length of 5/3 inches and a width of 13/4 inches
and a height of 5/2 inches. What is the volume of the second tray?
Answers
Answer: approx 13.54 (full decimal : 13.416666667)
Step-by-step explanation:
Area = Base Area x Height OR Length x Width x Height
5/3 x 13/4 x 5/2
5 x 13 x 5 = 325
3 x 4 x 2 = 24
325/24 = approx 13.54
HELP ASAP!! ILL MARK BRAINLIEST!! Anna must solve this equation.
(x^2)/4=x
Which three steps could Anna use to correctly solve the equation? Select from the drop-down menus to order the steps used to solve the equation.


Answers
Answer:
question 1:
step #1:divide both sides by x
step #2:multiply both sides by 4
step #3: plug it into equation
Step-by-step explanation:
question 1:
step #1: divide both sides by x
you get x/4 = 1
step #2:multiply both sides by 4
you get x = 4
step #3: plug it into equation
4 squared/4 = 4
Suppose that X has a hypergeometric distribution with N = 100, n = 4, and K = 20. Determine the following: a. P(X = 1) b. P(X = 6) c. P(X = 4) d.
Answers
The probabilities for the hypergeometric distribution with the given parameters are:
a. P(X = 1) ≈ 0.000407
b. P(X = 6) = 0
c. P(X = 4) ≈ 0.098117
d. P(X = 0) ≈ 1.97e-05
What is probability?Probability is a measure of the likelihood of an event to occur. Many events cannot be predicted with total certainty.
To determine the probabilities for the hypergeometric distribution with the given parameters, we can use the following formula:
P(X = k) = (choose(K, k) * choose(N-K, n-k)) / choose(N, n)
where "choose(a, b)" represents the binomial coefficient, calculated as a! / (b! * (a - b)!)
Let's calculate the probabilities:
a. P(X = 1):
P(X = 1) = (choose(20, 1) * choose(100-20, 4-1)) / choose(100, 4)
= (20 * 80) / 3921225
≈ 0.000407
b. P(X = 6):
P(X = 6) = (choose(20, 6) * choose(100-20, 4-6)) / choose(100, 4)
= (38760 * 0) / 3921225
= 0
c. P(X = 4):
P(X = 4) = (choose(20, 4) * choose(100-20, 4-4)) / choose(100, 4)
= (4845 * 80) / 3921225
≈ 0.098117
d. P(X = 0):
P(X = 0) = (choose(20, 0) * choose(100-20, 4-0)) / choose(100, 4)
= (1 * 77) / 3921225
≈ 1.97e-05
Therefore:
a. P(X = 1) ≈ 0.000407
b. P(X = 6) = 0
c. P(X = 4) ≈ 0.098117
d. P(X = 0) ≈ 1.97e-05
Learn more about probability on:
https://brainly.com/question/13604758
#SPJ4
The complete question is:
Suppose that X has a hypergeometric distribution with N = 100, n = 4, and K = 20. Determine the following: a. P(X = 1) b. P(X = 6) c. P(X = 4) d. P(X = 0).
The data set shows the numbers of hours that college students studied in one month.
What is the mean number of hours they studied in one month? Round answer to the tenths place. If answer is a whole number then include a zero in the tenths place to have answer counted correct.
76, 68, 22, 76, 82, 22
Answers
The mean number of hours studied in one month is 57.66
What is the mean ?
The input numbers are averaged mathematically to produce the mean. As a result, the mean is frequently referred to as the "average" in mathematics. A list of values, such as measurements or numbers, is used to calculate it by dividing the total number of values in the list by the total number of values in the list. To find the mean, add up each value in the set. After that, divide the sum by the variety of values.Mean = total number / the sum of the numbers
= 76 + 68 + 22 + 76 + 82 + 22 / 6
= 346/6
= 57.66
Learn more about mean
brainly.com/question/10853033
#SPJ9
Solve for x
A. Solve using the change of base formula.
Logby= log y/log b
B. Solve using a different method.
C. verify your solutions by substituting your value back into the original equation.

Answers
A) By using the change of base formula, the solution of the expression is,
⇒ x = - 2/3
B) The solution of the expression is,
⇒ x = - 2/3
What is an expression?Mathematical expression is defined as the collection of the numbers variables and functions by using operations like addition, subtraction, multiplication, and division.
Given that;
The expression is,
⇒ 5³ˣ⁻² = 125²ˣ
Now, We have the change of base formula,
⇒ \(log_{b} y = \frac{log y}{log b}\)
Here, The expression is,
⇒ 5³ˣ⁻² = 125²ˣ
⇒ 5³ˣ⁻² = 5⁶ˣ
Take log on both side,
⇒ log 5³ˣ⁻² = log 5⁶ˣ
⇒ (3x - 2) log 5 = 6x log 5
⇒ 3x - 2 = 6x
⇒ - 2 = 6x - 3x
⇒ 3x = - 2
⇒ x = - 2/3
B) By using another method as;
The expression is,
⇒ 5³ˣ⁻² = 125²ˣ
⇒ 5³ˣ⁻² = 5⁶ˣ
By comparing we get;
⇒ 3x - 2 = 6x
⇒ - 2 = 6x - 3x
⇒ 3x = - 2
⇒ x = - 2/3
Learn more about the mathematical expression visit:
brainly.com/question/1859113
#SPJ1
The______of the rectangular prism is 52 square units because LaTeX: 8+8+6+6+12+12=528+8+6+6+12+12=528+8+6+6+12+12=52.

Answers
I believe its area I'm doing the same thing
consider functions f and g what is the value of x when (fog)(x)=-8?

Answers
\((f\circ g)(x)=f(g(x))\)
So
\((f\circ g)(x)=-8\Leftrightarrow f(g(x))=-8\Rightarrow g(x)=-4\Rightarrow x=3\)
A recipe calls for 2 2/3 cups of flour to make two regular batches of cookies. Shiloh needs to make multiple batches of cookies. Represent this situation with an equation. What is the constant of proportionality? How can you identify it in an equation? How can you use an equation to determine if a relationship is proportional?
Answers
This situation can be represented with an equation as y = mx + b. The constant of proportionality (m) is a number that represents how much flour is needed for each additional batch of cookies. If the equation is in the form y = mx + b, then the relationship is proportional.
Shiloh needs to make multiple batches of cookies from a recipe that calls for 2 2/3 cups of flour to make two regular batches. To represent this situation in an equation, the equation is y = mx + b, where y is the amount of flour needed for the number of batches (x) Shiloh is making, m is the constant of proportionality, and b is the initial amount of flour needed (2 2/3 cups).
The constant of proportionality (m) in the situation above is the measure of how much flour is needed for each additional batch of cookies. For example, if the constant of proportionality is 0.75, that means Shiloh would need to add 0.75 cups of flour for each additional batch of cookies.
Therefore, if Shiloh is making three batches of cookies, the equation would be y = 0.75x + 2 2/3, and the total amount of flour needed would be 4 1/8 cups (2 2/3 + 0.75 + 0.75).
By using an equation to represent this situation, it is easy to determine if a relationship is proportional.
If the equation is in the form y = mx + b, then the relationship is proportional.
To learn more about equation, click here:
https://brainly.com/question/2972832
#SPJ4