What is the slope of a line that is parallel to the line y = 3/4x + 2?
Answers
when it’s parallel it has the same slope!
Related Questions
A person places $48800 in an investment account earning an annual rate of 3.1%,
compounded continuously. Using the formula V = Pert, where Vis the value of the
account in t years, P is the principal initially invested, e is the base of a natural
logarithm, and r is the rate of interest, determine the amount of money, to the
nearest cent, in the account after 13 years.
Answers
When a person places $48,800 in an investment account at an annual rate of 3.1% compounded continuously, using the formula, V = \(Pe^rt\), the amount of money (future value) after 13 years is $73,019.78.
What is compounding?Compounding refers to the process or interest system that computes periodic or continuous interest on both the principal and accumulated interest.
We can solve for the future value of an investment under continuous compounding using an online finance calculator as follows:
Using the formula V = \(Pe^rt\)
Principal (P) = $48,800.00
Annual Rate (R) = 3.1%
Compound (n) = Compounding Continuously
Time (t in years) = 13 years
Result:
V = $73,019.78
V = P + I where
P (principal) = $48,800.00
I (interest) = $24,219.78
Calculation Steps:
First, convert R as a percent to r as a decimal
r = R/100
r = 3.1/100
r = 0.031 rate per year,
Solving the equation for V:
V = \(Pe^rt\)
V = \(48,800.00(2.71828)^(0.031)(13)\)
V = $73,019.78
Learn more about continuous compounding at https://brainly.com/question/30460031.
#SPJ1
Suppose the weights of apples are normally distributed with a mean of 85 grams and a standard deviation of 8 grams. The weights of oranges are also normally distributed with a mean of 131 grams and a standard deviation of 20 grams. Amy has an apple that weighs 90 grams and an orange that weighs 155 grams.
Required:
a. Find the probability a randomly chosen apple exceeds 100 g in weight.
b. What weight do 80% of the apples exceed?
Answers
Answer:
a) 0.0304 = 3.04% probability a randomly chosen apple exceeds 100 g in weight.
b) The weight that 80% of the apples exceed is of 78.28g.
Step-by-step explanation:
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Weights of apples are normally distributed with a mean of 85 grams and a standard deviation of 8 grams.
This means that \(\mu = 85, \sigma = 8\)
a. Find the probability a randomly chosen apple exceeds 100 g in weight.
This is 1 subtracted by the p-value of Z when X = 100. So
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{100 - 85}{8}\)
\(Z = 1.875\)
\(Z = 1.875\) has a p-value of 0.9697
1 - 0.9696 = 0.0304
0.0304 = 3.04% probability a randomly chosen apple exceeds 100 g in weight.
b. What weight do 80% of the apples exceed?
This is the 100 - 80 = 20th percentile, which is X when Z has a p-value of 0.2, so X when Z = -0.84.
\(Z = \frac{X - \mu}{\sigma}\)
\(-0.84 = \frac{X- 85}{8}\)
\(X - 85 = -0.84*8\)
\(X = 78.28\)
The weight that 80% of the apples exceed is of 78.28g.
¼ y + ⅜ ? I don't know what to do
Answers
Answer:
isn't that a graph perhaps ?
Factor 27b - 18.
Write your answer as a product with a whole number greater than 1.
Answers
fill in the blanks then, choose the property of addition you used
1. 8+5=__ +8
2. 6+__= 6
3. (7 + 2) + 6 = __ + (2 + 6)
Answers
The graph of the function B is shown below. If B(x) = -1, then what is x? -1 1 2 NEXT QUESTION
Answers
Answer:
x is -1/b yw
Step-by-step explanation:
Question One:
If a raw score corresponds to a z-score of 1.75, what does that tell you about that score in relation to the mean of the distribution?
Question Two:
What if the raw score corresponds to a z-score of -0.85?
Answers
Question One:A positive z-score indicates that the raw score is above the mean, while a negative z-score indicates that the raw score is below the mean.
Question Two: , the raw score is relatively lower than the mean.
If a raw score corresponds to a z-score of 1.75, it tells us that the raw score is 1.75 standard deviations above the mean of the distribution. In other words, the raw score is relatively higher than the mean. The z-score provides a standardized measure of how many standard deviations a particular value is from the mean.
A positive z-score indicates that the raw score is above the mean, while a negative z-score indicates that the raw score is below the mean.
Question Two:
If a raw score corresponds to a z-score of -0.85, it tells us that the raw score is 0.85 standard deviations below the mean of the distribution. In other words, the raw score is relatively lower than the mean. The negative sign indicates that the raw score is below the mean.
To understand the meaning of a z-score, it is helpful to consider the concept of standard deviation. The standard deviation measures the average amount of variability or spread in a distribution. A z-score allows us to compare individual data points to the mean in terms of standard deviations.
In the case of a z-score of -0.85, we can conclude that the raw score is located below the mean and is relatively lower compared to the rest of the distribution. The negative z-score indicates that the raw score is below the mean and is within the lower portion of the distribution. This suggests that the raw score is relatively smaller or less than the average value in the distribution.
By using z-scores, we can standardize and compare values across different distributions, allowing us to understand the position of a raw score relative to the mean and the overall distribution.
For mor such question mean visit
https://brainly.com/question/1136789
#SPJ8
What value of a, b, and c make this equation true?

Answers
Answer:
I think you need to know the value of X to get this answer.
Step-by-step explanation:
PLSSS If you spin the spinner 10 times, what is the best prediction possible for the number of times it will land on pink?

Answers
Answer:
3 timesStep-by-step explanation:
Probability of landing on pink:
P(pink) = number of pink / total number = 3/10If spun 10 times then possible outcomes with pink:
3/10*10 = 3 timesAnswer:
3 times, or \(\frac{3}{10}\)
Step-by-step explanation:
There are 3 out of 10.
A boat travels with velocity vector (25, 25√3). What is the directional bearing of the boat?
ON 30° E
OE 30° S
OE 30° N
ON 30° W
Answers
In a case whereby a boat travels with velocity vector (25, 25√3) the directional bearing of the boat is ON 30° E.
How can the directional bearing of the boat be determined?The given velocity vector are; 25 and 25√3)
horizontal components =25
vertical components =25√3
Then the angle
Tan(θ) = {vertical component / horizontal component }
= 25√3 / 25
= √3 / 1
= √3
Tangent √3= 60 degrees, Then the directional bearing of angle 60 degrees is 30° E
Learn more about bearing at:
https://brainly.com/question/19710752
#SPJ1
prove the divisibility rule by three, which states that a number is divisible by 3 if and only if the sum of its digits is divisible by 3.
Answers
The divisibility rule for 3 on any integer number is proven in the detailed explanation of the solution.
Given a non-decimal number, n.
Suppose n may be divided by 3.
n should be thought of in terms of its digits as
n = d × 1 × 10⁽ⁿ⁻¹⁾⁽ⁿ⁻¹⁾ + d × 2 × 10⁽ⁿ⁻²⁾ + ... + d × m × 10⁰
where d 1, d 2,..., d m are its digits and m is the number of digits in n.
The result of the preceding equation with n = 3k is
3k = d × 1 × 10(m-1) + d × 2 × 10(m-2) +... + d × m × 10(m-0)
3000 is subtracted from both sides of the equation, giving us
0 = d × 1 × 10⁽ⁿ⁻¹⁾⁽ⁿ⁻¹⁾ + d × 2 × 10⁽ⁿ⁻²⁾ + ... + d × m × 10⁰
We obtain by adding 3k to both sides of the equation.
3k = d × 1 × 10⁽ⁿ⁻¹⁾+ d
The divisibility rule is a heuristic for determining if two positive integers can be divided evenly (i.e. there is no remainder left over). For instance, determining if a number's last digit is 2, 4, 6, 8, or 0 makes it simple to determine whether it is even.
By examining the digits of the number, a divisibility rule provides a simple shorthand for determining if an integer is divisible by a particular set of factors without actually doing the division. This page only offers recommendations and examples for decimal, or base 10, numbers despite the fact that there are distinct divisibility tests for numbers in each radix or basis.
Learn more about divisibility rule here:
https://brainly.com/question/28281492
#SPJ4
Solve each proportion

Answers
Answer:
D
Step-by-step explanation:
the correct answer is D
Help asap
in each of the following replace the * with the smallest digit to make it divisble by 11
7,01,69,30*
Answers
The smallest number that will make it divisible by 11 is n = 2 and the number is A = 7,01,69,302
Given data ,
Let the missing number be represented as n
Now , the value of the original number is A = 7,01,69,30*
where * represents = n
To make a number divisible by 11, the difference between the sum of the digits in the odd-numbered positions and the sum of the digits in the even-numbered positions must be a multiple of 11.
On simplifying the equation , we get
To make the difference between the sums a multiple of 11, we need to add the smallest digit to the end. The smallest digit is 8
Hence , the number that is divisible by 11 is 7,01,69,302
To learn more about equations click :
https://brainly.com/question/19297665
#SPJ1
Helpppp meeeeeeee (35 points)
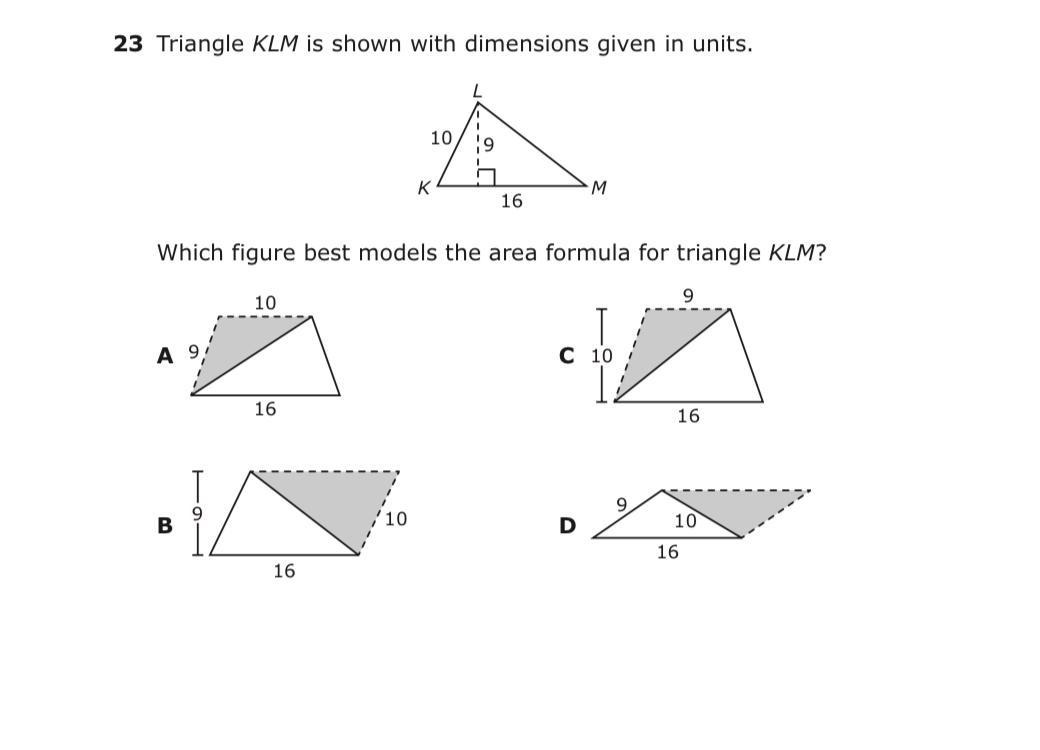
Answers
Answer:
B.
Step-by-step explanation:
It is B because the height of the triangle is 9 and the height of B is 9. The bottom side of the triangle is 16 and the bottom of B is 16. The other labeled side is 10 and the side parallel to that side is 10 in figure B.
What percent of 28 is 77?
Answers
Answer:
36.3636364%
or 36.36
Step-by-step explanation:
Is how old are you? a statistical question
Answers
Answer:
Hey!
NO IT IS NOT A STATISTICAL QUESTION!
Step-by-step explanation:
This is because you are including ONLY YOU...this wont work as statistics take data from a COLLECTION of people or things!
So a better question will be :
HOW OLD ARE THE PEOPLE IN MY NEIGHBORHOOD?
(averages)
HOPE THIS HELPS!!
Help due soon plz helpp

Answers
Answer: 7) -12;
8) 0 или 1.
Step-by-step explanation:
7.
x ≤ - 12
x ∈ ( - ∞; - 12]
Наибольшее целое значение, при котором верно неравенство равно -12.
8.
-9,6*8 > - 9,627
Варианты возможных чисел: -9,618 и -9,608.
Значит вместо звездочки можно подставить цифры 0 или 1.
tristan wants to build a square garden in his backyard. if the garden is going to be 64 ft squared how many feet of material will he need for the perimeter of the garden?
Answers
Answer:
32 ft
Step-by-step explanation:
First Tristan must determine the length of one side of his square garden. Sine A = x^2, where x is the length of one side, and since 64 ft^2 = x^2, we can find the length x by taking the square root of both sides: 8 ft = x.
Now the length of the material enclosing the garden is the perimeter, P.
For a square, P = 4x.
Therefore, in this case, P = 4(8 ft) = 32 ft
If y is inversely proportional to the square root of x and y=61 when x=9, find y if x=81. (Round off your answer to the nearest hundredth.)
Answers
\(\qquad \qquad \textit{inverse proportional variation} \\\\ \textit{\underline{y} varies inversely with \underline{x}} ~\hspace{6em} \stackrel{\textit{constant of variation}}{y=\cfrac{\stackrel{\downarrow }{k}}{x}~\hfill } \\\\[-0.35em] ~\dotfill\\\\ \stackrel{\textit{\underline{y} is inversely proportional to the square root of \underline{x}}}{y = \cfrac{k}{\sqrt{x}}}~\hfill \stackrel{\textit{we also know that}}{ \begin{cases} y = 61\\ x = 9 \end{cases}}\)
\(61=\cfrac{k}{\sqrt{9}}\implies 61=\cfrac{k}{3}\implies 183=k~\hfill \boxed{y = \cfrac{183}{\sqrt{x}}} \\\\[-0.35em] ~\dotfill\\\\ \stackrel{\textit{when x = 81, what is "y"?}}{ y = \cfrac{183}{\sqrt{81}}\implies y=\cfrac{183}{9}}\implies y = \cfrac{61}{3}\implies y = 20.\overline{3}\implies y = \stackrel{\textit{rounded up}}{20.33}\)
2. Troy had 3/8 of a pizza left over from his party. He ate 3/4 of the leftover pizza for breakfast. How much of the
whole pizza did Troy have at breakfast?
3. 3/5 of a bag of coffee weighs 6/7 pound. How much does a whole bag of coffee weigh?
Answers
The 9/32 of whole pizza Troy had for breakfast. The whole bag of coffee weighs 10/7 pounds
A fraction is defined as a part of a whole quantity.
1. Leftover pizza = 3/8
Pizza used as breakfast = 3/4 of left-over pizza
= 3/4 of 3/8
The of is calculated by the use of multiplication
The fractions are multiplied as follows:
The numerators of the fractions are multiplied and written as the numerator.The product of the denominators is written as the denominator.Then we simplify the given fraction to get the final result.Pizza used as breakfast = 3/4 * 3/8
= 3 * 3 / 4 * 8
= 9/32
2. 3/5 of bag of coffee weighs = 6/7 pounds
1 bag of coffee weighs = 6/7 ÷ 3/5
The fractions are divided as follows:
The fraction to be divided is reciprocatedThe numerators of the fractions are multiplied and written as the numerator.The product of the denominators is written as the denominator.Then we simplify the given fraction to get the final result.Thus, = 6/7 * 5/3
= 6 * 5 / 7 * 3
= 30/21
= 10/7 pounds
Learn more about Fraction:
https://brainly.com/question/29369267
#SPJ1
Levy is painting a miniature model of a World War II tank. His figure uses a 1:72 scale and is 22.5 cm
long. How many centimeters long was the actual tank?
cm
Answers
Levy is painting a miniature model of a World War II tank. His figure uses a 1:72 scale and is 22.5 cm long. The actual tank is 1620 cm long.
To determine the length of the actual tank, we need to scale up the length of the miniature model using the given scale of 1:72.
Let's denote the length of the actual tank as "x".
According to the scale, 1 cm on the miniature model represents 72 cm on the actual tank.
So, we can set up the following proportion:
1 cm (miniature model) / 72 cm (actual tank) = 22.5 cm (miniature model) / x cm (actual tank)
Cross-multiplying and solving for x, we get:
x = (72 cm * 22.5 cm) / 1 cmx = 1620 cm
The actual tank is 1620 cm long.
For more such questions on miniature model
https://brainly.com/question/14657504
#SPJ8
Draw the net and calculate the surface area .

Answers
Hello!
surface area
= 2(4 x 2) + 2(12 x 4) + 2(12 x 2)
= 160cm²
126720 inches are equal to what miles
Answers
Answer:
2 miles
Step-by-step explanation:
Divide 126720 by 63360.
Answer:
the answer is 2 miles
Step-by-step explanation:
(hope this helps)
how do you Simplify 6(x + 3).
Answers
Answer:
6x+18
Step-by-step explanation:
6(x + 3).
Distribute
6x+6*3
6x+18
Suppose we have a random sample of size n = 5 from a continuous uniform distribution on the interval [0, 1]. Find the probability that the third largest observation in the
sample is less than 0.7.
Answers
The probability that the third largest observation in the sample is less than 0.7 is 0.2401 = 24.01%.
How do we calculate?The sample size n = 5,
Therefore the order statistics will be represented as X₁, X₂, X₃, X₄, and X₅.
Probability that X₃ is less than 0.7:
Since X₃ is the third largest observation = (X₁ and X₂) < 0.7.
The probability that X₃ is less than 0.7 is (0.7)² = 0.49.
The Probability that X₁ and X₂ < or equal to 0.7 is found as:.
The probability that both X₁ and X₂ are less than or equal to 0.7 is (0.7)² = 0.49 because in a continuous uniform distribution, the probability of any single observation being less than 0.7 is 0.7 - 0 = 0.7.
We then get the product of both cases:
Probability = 0.49 * 0.49 = 0.2401
Learn more about Probability at:
https://brainly.com/question/24756209
#SPJ1
Solve each system by the substitution method. If there is no solution or an infinite number of solutions, so state. Use set notation to express solution sets.

Answers
Given:
y=3x-5
21x - 35 = 7y
Substitute the first equation into the second equation.
21x - 35 = 7(3x-5)
Open the parenthesis
21x - 35 = 21x - 35
Collect like term
21x - 21x = -35 + 35
0 = 0
Since, the above statement is true, then it has infinitely many solutions.
.
Help if possible, thanks

Answers
Answer:
C
Step-by-step explanation:
Sara's speed is 10mph while Bob is 8mph
Sara did 10
Bob did 8
The difference is 2
Hope that helped *smiles*
which has the larger 15th term when comparing the arithmetric and geometric sequences below? show evidence that support your answer Arithmetic sequence: 150, 650, 1150, 1650Geometric sequence:4,12, 36, 108
Answers
Answer
For the arithmetic sequence,
15th term = 7,500
For the geometric sequence,
15th term = 19,131,876
We can see that the geometric sequence has the larger 15th term.
Explanation
The general formula for an arithmetic progression is
f(n) = a + (n - 1)d
where
a = first term = 150
n = number of terms
d = common difference
= (Second term) - (First term)
= (Third term) - (Second term)
= Difference between consecutive terms
= 650 - 150
= 500
f(n) = 150 + (n - 1)500
f(n) = 150 + 500n - 500
f(n) = -350 + 500n
For the 15th term, n = 15
f(n) = -350 + 500n
f(15) = -350 + 500(15)
f(15) = -350 + 7500
f(15) = 7,150
For the geometric sequence,
\(f(n)=ar^{n-1}\)where
a = first term = 4
n = number of terms
r = common ratio
= (Second term)/(First term)
= (Third term)/(Second term)
= Ratio of consecutive terms
= (12/4)
= 3
For the 15th term, n = 15
\(\begin{gathered} f(n)=ar^{n-1} \\ f(15)=4\times3^{15-1} \\ f(15)=4\times3^{14} \\ f(15)=19,131,876 \end{gathered}\)Hope this Helps!!!
Need help with math homework
e^x=10^(x-1)
Answers
Answer:
Step-by-step explanation:
This equation represents the relationship between the exponential functions y = e^x and y = (10^(x-1)). These two functions are equal to each other for all values of x. This can be shown by taking the natural logarithm of both sides of the equation, which gives us:
ln(e^x) = x-1
In this equation, ln(e^x) is equal to x, since the natural logarithm of an exponential expression with a base of e is the exponent. Therefore, we can simplify the equation by taking the natural logarithm of both sides:
ln(10^(x-1)) = x-1
e^(x-1) = 10^x
The two functions e^x and 10^(x-1) are the same function with different bases, so they follow the same pattern. The fact that these two functions are equal to each other for all values of x can also be shown by graphing the two functions and seeing that they overlap perfectly.
22. Volume of Water in a Reservoir.
A reservoir shaped like a
hemispherical bowl of radius 8 m is filled with water to a depth
of 4 m.
(a) Find an estimate S of the water's volume by approximating the
water with eight circumscribed solid cylinders.
(b) It can be shown that the water's volume is V = (320•pi)/3 m³.
Find the error |V-S| as a percentage of V to the nearest
percent.
Answers
On solving the provided question, we can say that Volume of cylinder, V = \(\pi r^2 X h\) => V = 3.14 * 8*8*4 = 803.84 cubic m
what is cylinder?One of the most fundamental curved geometric forms is the cylinder, which is often a three-dimensional solid. It is referred to as a prism with a circle as its base in elementary geometry. Several contemporary fields of geometry and topology also define a cylinder as an indefinitely curved surface. A three-dimensional object known as a "cylinder" consists of curving surfaces with circular tops and bottoms. A cylinder is a three-dimensional solid figure that has two bases that are both identical circles joined by a curving surface at the height of the cylinder, which is determined by the distance between the bases from the center. Examples of cylinders are cold beverage cans and toilet paper wicks.
here,
we have a cylinder
and,
radius, r = 8m
height, h = 4m
Volume, V = \(\pi r^2 X h\)
V = 3.14 * 8*8*4 = 803.84 cubic m
To know more about cylinder visit:
https://brainly.com/question/16134180
#SPJ1