what is the slope of (-3,4) (-2,0)
Answers
Answer:
m = − 4
Step-by-step explanation:
Use the slope formula to find the slope m
Hope this helps :)

Related Questions
Ken owns 500 shares of LaceNBrace, which makes hockey equipment. He receives a notice stating the company will be paying $0.15 dividend per share. What is the total dividend payment he receives for that quarter? O $750 O $8.50 O $7.55 O $75
Answers
Ken will receive a total dividend payment of $75 for that quarter.
We have to given that,
Ken owns 500 shares of LaceNBrace, which makes hockey equipment.
And, He receives a notice stating the company will be paying $0.15 dividend per share.
Now, For the total dividend payment Ken receives for that quarter, we can multiply the dividend per share by the total number of shares he owns:
= $0.15 per share x 500 shares
= $75
Therefore, Ken will receive a total dividend payment of $75 for that quarter.
Learn more about the divide visit:
https://brainly.com/question/28119824
#SPJ1
jenni wrote a rational number that is positive which of the following us not a possible number she wrote? a. 0 b. 1 c. 7/8 d . 5 1/4
Answers
if D equals 4x + 10 e f equals 2x - 1 + d f equals 9 x - 15 find DF
Answers
Answer:
4x+10+2x-1=9x-15;
6x+9=9x-15;
6x-9x=-15-9;
-3x=-24;
3x=24;
from which
x=24:3=8
Then:
DF=9x-15=(9×8)-15=72-15=57
Was this helpful
Consider the function shown on the graph.

Answers
Answer:
C.) y = 3(x - 3)(x - 7)
For the function:
x intercept: (3, 0), (7, 0)vertex point: (5, -12)point: (8, 15)Writing equation:
y = a(x - h)² + k
15 = a(8 - 5)² - 12
15 = 9a - 12
9a = 15 + 12
9a = 27
a = 3
So the equation is:
y = 3(x - 5)² - 12
y = 3(x² - 10x + 25) - 12
y = 3x² - 30x + 63
y = 3(x - 3)(x - 7)
Find the value of L that Will Maximize the profit Q=L²e^0.01L
Answers
The minimum profit occurs at L = 0, where Q = 0.
To find the value of L that maximizes the profit Q = L²\(e^{(0.01L)\).
We need to differentiate Q with respect to L and find the critical points where the derivative equals zero.
Then we can determine whether each critical point is a maximum or a minimum by examining the second derivative.
Testing for critical points:Q = L²\(e^{(0.01L)\)
Q' = \(2Le^{(0.01L)\) + \(0.01 L^2e^{(0.01L)\)
= 0(2L + 0.01L²) \(e^{(0.01L)\)
= 0L (critical point) or 200 \(e^{(0.01L)\)
= 0 (extraneous, ignore)
2L + 0.01L² = 0L(2 + 0.01L) = 0L = 0 or L = -200 (extraneous, ignore)
The only critical point is at L = 0.
Testing for maximum or minimum:Q'' = \(2e^{(0.01L)\) + 0.02Le^(0.01L) + 0.0001L²\(e^{(0.01L)Q''(0)\)
= \(2e^{(0)\) = 2Since Q''(0) > 0,
The critical point at L = 0 is a minimum.
Therefore, there is no value of L that maximizes the profit.
For more related questions on minimum profit:
https://brainly.com/question/32510275
#SPJ8
The values of L that will maximize the profit are 0 and -200
Finding the value of L that will maximize the profitFrom the question, we have the following parameters that can be used in our computation:
\(Q = L\²e^{0.01L\)
Differentiate the function
So, we have
\(Q' = \frac{L \cdot (L + 200) \cdot e^{0.01L}}{100}\)
Set the equation to 0
\(\frac{L \cdot (L + 200) \cdot e^{0.01L}}{100} = 0\)
Cross multiply
\(L \cdot (L + 200) \cdot e^{0.01L} =0\)
When expanded, we have
L = 0, L + 200 = 0 and \(e^{0.01L} =0\)
When solved for L, we have
L = 0 and L = -200
Hence, the values of L are 0 and -200
Read more about functions at
https://brainly.com/question/32616074
#SPJ1
Keith tabulated the following values for time spent napping in minutes of six of his friends: 23, 35, 17, 30, 20, and 19. The standard deviation is 7.043 Keith reads that the mean nap is 22 minutes. The t-statistic for a two-sided test would be __________. Answer choices are rounded to the hundredths place. 1.39 or 1.43 or 2.88 or 0.70
Answers
Answer:
The t-statistic is \(t = 0.6956\)
Step-by-step explanation:
From the question we are told that
The population mean is \(\mu = 22 \ minutes\)
The standard deviation is \(s = 7.043\)
The given data is 23, 35, 17, 30, 20, and 19.
Generally the sample mean is mathematically evaluated as
\(\= x = \frac{23+ 35+17+ 30+ 20+ 19 }{6}\)
\(\= x =24\)
The t-statistic is mathematically evaluated as
\(t = \frac{ \= x - \mu }{\frac{s}{ \sqrt{n} } }\)
=> \(t = \frac{ 24 - 22 }{\frac{ 7.043}{ \sqrt{6} } }\)
=> \(t = 0.6956\)
Answer: 0.70
Step-by-step explanation:
The sum of three consecutive numbers is 150. Find them.
Answers
The sum of three consecutive numbers for 150 is 49,50,51.
Three consecutive numbers: x+(x+1)+(x+2)
x+x+1+x+2= 150
3x+3 = 150
3x = 150-3
3x= 147
X = 147/3
49 =x
But we also need to find (x+1) and (x+2)
49+1= 50
49+2= 51
49+50+51 = 150
The three consecutive numbers are 49,50,51.
Meaning: Numbers that follow one another numbers sequentially are known as consecutive numbers. The difference between any two numbers is always 1. A series of numbers' mean and median are equal. If n is a number, then it follows that n, n+1, and n+2 are also numbers. Examples. 1, 2, 3, 4, 5.
For such more question on sum:
brainly.com/question/10662517
#SPJ4
if x=3, what is Y?
x= -3,0,3,6
y= -5,-4,-3,-2
Answers
Answer:
If x = 3, then y = -2 since the corresponding value of y for x=3 is -2 in the given table.
Step-by-step explanation:
how do i solve for m in i=pm
Answers
Answer:
Divide by P
Step-by-step explanation:
i = P x M
divide by P to get M alone, which means you have to do it to both sides
i/P = M
the sum of four number is 20500.three of the numbers are 2341.578 and 10690.What is the fourth number?
Answers
Answer:
5216.844
Step-by-step explanation:
Let x be the fourth number.
We know that the sum of the four numbers is 20500:
2341.578 + 10690 + x + 2341.578 = 20500
Simplifying and solving for x:
x = 20500 - 2341.578 - 10690 - 2341.578
x = 5216.844
Which of the following equations represents the line with a slope of 2 and a y-intercept of 4?
y = 2x + 4
y = 1/2x - 4
y = 2x - 4
y = 1/2x + 4
Answers
Answer:
The equation of the line with a slope of 2 and a y-intercept of 4 in the slope-intercept is:
y = 2x + 4Hence, option 'A' is correct.
Step-by-step explanation:
The slope-intercept form of the line equation
y = mx+b
where
m is the slope b is the y-interceptIn our case, we are given
Slope m = 2y-intercept b = 4substituting m = 2 and b = 4 in the slope-intercept form of the line equation
y = mx+b
y = 2x + 4
Therefore, the equation of the line with a slope of 2 and a y-intercept of 4 in the slope-intercept is:
y = 2x + 4Hence, option 'A' is correct.
J is between points X and Y. XY = 27 and JY= 5. What is XJ?
Answers
Answer:22
Step-by-step explanation:27-5
The length of the window is 2m longer than its width and the area is 32m^
Answers
Answer:
X¹= -2 + 2√33
X²= -2 - 2√33
Step-by-step explanation:
X × (X+2) = 32
X² + 2X = 32
X² + 2X - 32= 0
Δ=132
X= -2 ± 2√33
X¹= -2 + 2√33
X²= -2 - 2√33
(You can change the 2√33 to 11,5 if you want to)
Simplify y² + 11y - 6y + y²,
Answers
In order to simplify the expression
y² + 11y - 6y + y²,
we just have to add the terms with the same unkowns or combine like terms
terms with y: +11y and -6y
terms with y²: +y² and +y²
Now, we combine like terms:
terms with y: +11y - 6y = 5y
terms with y²: +y² + y² = 2y²
Then
y² + 11y - 6y + y²
= 2y² + 5y
Answer: y² + 11y - 6y + y² = 2y² + 5y
7. Ukuthuthuka Ngesivinini Kwezobuchwepheshe Kunomthelela Omuhle
Nomubi Kwezomnotho .[50]
Answers
Answer:
Thanks
Step-by-step explanation:
and also check out the language
Which of the following systems of inequalities has point D as a solution?

Answers
Answer:
f(x) \(\leq\) 3x + 4
g(x) ≥ -1/2x - 5
Step-by-step explanation:
Point D is below f(x) and above g(x)
Helping in the name of Jesus.
Use the graph to answer the question about discontinuity refer to image
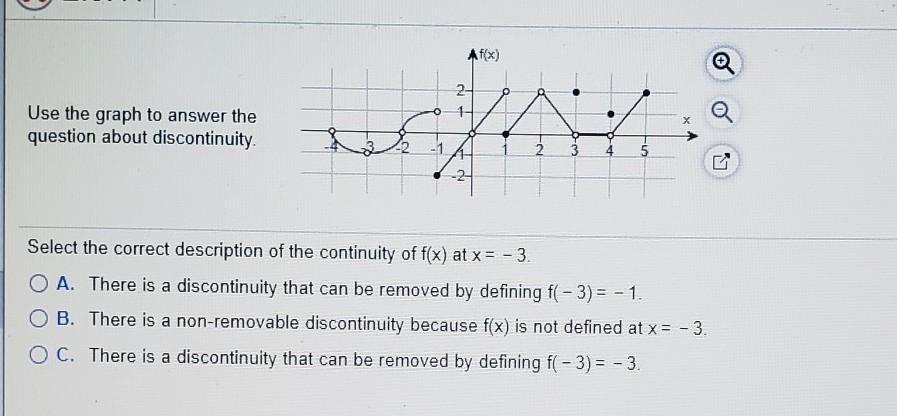
Answers
Given the graph of the function
We will check the discontinuity of the function at x = -3
So, as shown in the graph :
as the function reach to x = -3 from the right and the left , the value of the function = -1
But at x = -3 , the function does not have a value
So, there is a discontinuity at x = -3, but can be removed if f(-3) = -1
So, the answer is : option A
There is a discontinuity that can be removed by defining f(-3) = -1
If a data set has an even number of observations, the median _____
Answers
4.53x 11 What is the product of the two factors?
Answers
Answer:
4.53 x 11 = 49.83
Suppose you're making a soup that uses 5 cups of chicken broth for 8 servings. You need to make 12 servings of the soup. How much broth do you need?
A) 7.5 cups
B) 2.5 cups
C) 8.7 cups
D) 10 cups
Answers
Represent the following sentence as an algebraic expression, wher
number" is the letter x. You do not need to simplify.
The product of 8 and the sum of a number and 5.
F
Answers
Answer: 8 (5+x)
Step-by-step explanation:
URGENT!! ILL GIVE BRAINLIEST! AND 100 POINTS
Fill in the banks if you had this question before!!

Answers
An equation for the total cars and trucks for dealership A is: x + y = 164.
An equation for the total cars and trucks for dealership B is: 2x + 0.5y = 229.
The number of cars that dealership A sold is: 98 cars.
The number of trucks that dealership B sold is: 66 trucks.
How to write a system of equations to model this situation?In order to write a system of linear equations to describe this situation, we would assign variables to the number of cars sold and number of trucks sold, and then translate the word problem into an algebraic equation as follows:
Let the variable x represent the number of cars sold.Let the variable y represent the number of trucks sold.Since the first dealership sold a total of 164 cars and trucks, a linear equation to model this situation is given by;
x + y = 164.
Additionally, the second dealership sold twice as many cars and half as many trucks as the first dealership, with a total of 229 cars and trucks;
2x + 0.5y = 229.
By solving the systems of linear equations simultaneously, we have:
2x + 0.5(164 - x) = 229
1.5x + 82 = 229
x = 98 cars.
For the y-value, we have;
2(98) + 0.5y = 229
0.5y = 229 - 196
y = 33/0.5
y = 66 trucks.
Read more on solution and equation here: brainly.com/question/25858757
#SPJ1
If sum of first 6 digits of AP is 36 and that of the first 16 terms is 255,then find the sum of first ten terms.
•Please answer it correctly ( step by step)
Answers
Answer:
100
Step-by-step explanation:
We have the sum of first n terms of an AP,
Sn = n/2 [2a+(n−1)d]
Given,
36= 6/2 [2a+(6−1)d]
12=2a+5d ---------(1)
256= 16/2 [2a+(16−1)d]
32=2a+15d ---------(2)
Subtracting, (1) from (2)
32−12=2a+15d−(2a+5d)
20=10d ⟹d=2
Substituting for d in (1),
12=2a+5(2)=2(a+5)
6=a+5 ⟹a=1
∴ The sum of first 10 terms of an AP,
S10 = 10/2 [2(1)+(10−1)2]
S10 =5[2+18]
S10 =100
This is the sum of the first 10 terms.
Hope it will help.
\(\sf\underline{\underline{Question:}}\)
If sum of first 6 digits of AP is 36 and that of the first 16 terms is 255,then find the sum of first ten terms.
$\sf\underline{\underline{Solution:}}$
$\sf\bold\purple{||100||}$$\space$
$\sf\underline\bold\red{||Step-by-Step||}$
$\sf\bold{Given:}$
$\sf\bold{S6=36}$ $\sf\bold{S16=255}$$\space$
$\sf\bold{To\:find:}$
$\sf\bold{The \: sum\:of\:the\:first\:ten\:numbers}$$\space$
$\sf\bold{Formula\:we\:are\:using:}$
$\implies$ $\sf{ Sn=}$ $\sf\dfrac{N}{2}$ $\sf\small{[2a+(n-1)d]}$
$\space$
$\sf\bold{Substituting\:the\:values:}$
→ $\sf{S6=}$ $\sf\dfrac{6}{2}$ $\sf\small{[2a+(6-1)d]}$
→ $\sf{36 = 3[2a+(6-1)d]}$
→$\sf{12=[2a+5d]}$ $\sf\bold\purple{(First \: equation)}$
$\space$
$\sf\bold{Again,Substituting \: the\:values:}$
→ $\sf{S16}$ $\sf\dfrac{16}{2}$ $\sf\small{[2a+(16-1)d]}$
→ $\sf{255=8[2a + (16-1)d]}$
:: $\sf\dfrac{255}{8}$ $\sf\small{=31.89=32}$
→ $\sf{32=[2a+15d]}$ $\sf\bold\purple{(Second\:equation)}$
$\space$
$\sf\bold{Now,Solve \: equation \: 1 \:and \:2:}$
→ $\sf{10=20}$
→ $\sf{d=}$ $\sf\dfrac{20}{10}$ $\sf{=2}$
$\space$
$\sf\bold{Putting \: d=2\: in \:equation - 1:}$
→ $\sf{12=2a+5\times 2}$
→ $\sf{a = 1}$
$\space$
$\sf\bold{All\:of\:the\:above\:eq\: In \: S10\:formula:}$
$\mapsto$ $\sf{S10=}$ $\sf\dfrac{10}{2}$ $\sf\small{[2\times1+(10-1)d]}$
$\mapsto$ $\sf{5(2\times1+9\times2)}$
$\mapsto$ $\sf\bold\purple{5(2+18)=100}$
$\space$
$\sf\small\red{||Hence , the \: sum\: of \: the \: first\:10\: terms\: is\:100||}$
_____________________________
Diane plans to arrive 30 minutes early on Friday. What time does she plan to arrive?
*
7:00 A.M.
8:30 A.M.
8:00 A.M.
6:30 A.M.
7:30 A.M.

Answers
Diane plans to arrive at 7:30 A.M.
What is time ?
Time is a notion that is used to quantify the length and progression of occurrences. It is a key aspect of how things work and can be expressed in terms of hours, minutes, seconds, and other time intervals. Time helps us schedule, coordinate, and comprehend the sequence of events in our daily lives. It also enables us to arrange and synchronize activities.
If we take the assumed intended arrival time of 8:00 A.M. and deduct Diane's anticipated arrival time of 30 minutes, we get the intended arrival time.
Therefore, Diane plans to arrive at 7:30 A.M.
Learn more about time here :brainly.com/question/24662469
#SPJ1
Was Thomas Jefferson a federalist or anti-federalist?
Answers
Answer:
He was an Anti-federalist
Step-by-step explanation:
Answer:
Anti-federalist
Step-by-step explanation:
The Federalists, led by Secretary of Treasury Alexander Hamilton, wanted a strong central government, while the Anti-Federalists, led by Secretary of State Thomas Jefferson, advocated states' rights instead of centralized power.
2040
3. The main engine alone on a rocket can consume the allotted
fuel supply in two-thirds the time it takes the auxiliary engine
alone. Working together they both consume their allotted fuel
in 36 seconds. Formulate an equation to represent the
situation. How long could each be fired alone?
Answers
Using equations, the time for the main engine 14.4 seconds and 21.6 seconds for the auxiliary engine
What is the equation to represent the situationLet's call the time each engine takes to consume its allotted fuel supply as "t₁" for the main engine and "t₂" for the auxiliary engine.
From the first piece of information, we know:
t₁ = (2/3)t₂
From the second piece of information, we know that the combined fuel consumption time for both engines is 36 seconds:
t₁ + t₂ = 36
Now we can substitute the first equation into the second:
t₁ + (2/3)t₂ = 36
Combining like terms:
t₂ = 21.6
Finally, substituting t₂ back into the first equation:
t₁ = (2/3)(21.6) = 14.4
So the main engine alone could be fired for 14.4 seconds and the auxiliary engine alone could be fired for 21.6 seconds.
Learn more on equations here;
https://brainly.com/question/18831322
#SPJ1
derivate (cos(3x^2). (5x^3 -1)^1/3 +sin 4x^3)^4
\( \: \: \: \: find \: first \: derivative \\ ( cos(3x {}^{2} ) \times ( \sqrt[3]{5x {}^{3} - 1} ) + \sin(4x {}^{3} ) {}^{4} \)
Answers
Answer:
Step-by-step explanation:
\(\frac{d}{dx} [cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)]^4\\\\=4[cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)]^3\; \frac{d}{dx} [cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)] --- eq(1)\)
Lets look at the derivative part:
\(\frac{d}{dx} [cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)] \\\\= \frac{d}{dx}[cos(3x^2) \sqrt[3]{5x^3 -1} ] + \frac{d}{dx}[sin(4x^3)]\\\\=cos(3x^2) \frac{d}{dx}[ \sqrt[3]{5x^3 -1} ] + \sqrt[3]{5x^3 -1}\frac{d}{dx}[ cos(3x^2) ] + cos(4x^3) \frac{d}{dx}[4x^3]\\\\=cos(3x^2) \frac{1}{3} (5x^3 -1)^{\frac{1}{3} -1} \frac{d}{dx}[5x^3 -1] + \sqrt[3]{5x^3 -1} (-sin(3x^2))\frac{d}{dx}[ 3x^2] + cos(4x^3)[(4)(3)x^2]\)
\(=\frac{cos(3x^2) 5(3)x^2}{3(5x^3 - 1)^{\frac{2}{3} }} -\sqrt[3]{5x^3 -1}\; sin(3x^2) (3)(2)x + 12x^2 cos(4x^3)\\\\=\frac{5x^2cos(3x^2) }{(5x^3 - 1)^{\frac{2}{3} }} -6x\sqrt[3]{5x^3 -1}\; sin(3x^2) + 12x^2 cos(4x^3)\)
Substituting in eq(1), we have:
\(\frac{d}{dx} [cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)]^4\\\\=4[cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)]^3\; [\frac{5x^2cos(3x^2) }{(5x^3 - 1)^{\frac{2}{3} }} -6x\sqrt[3]{5x^3 -1}\; sin(3x^2) + 12x^2 cos(4x^3)]\)
Find the surface area of the cylinder: Use 3.14 for
2 cm
15 cm
A. 100.48 cm
B. 97,43 cm
C. 36.28 cm
D. 33.14 cm
2 of 4 Answered

Answers
Answer:
Well on my end i got 47.12, with pi included
Step-by-step explanation:
The surface area of the cylinder with the diameter 2cm and height 15cm is \(100.48 \; cm^2\)
Calculation to find Surface area of cylinder:
Given the diameter of the cylinder is 2cm and height 15cm
Formula :
The surface area of the cylinder =\(2\pi r^2+2\pi rh\)
where 'r' is the radius and 'h' is the height of the cylinder
Diameter = 2cm
\(radius =\frac{diameter }{2} =\frac{2}{2} =1\)
radius = 1cm and height is 15 cm
the value of pi is 3.14
Substiute all the values
\(SA = 2\pi r^2+2\pi rh\\SA=2(3.14)(1)^2+2(3.14)(1)(15)\\SA=6.28+94.2\\SA=100.48 cm^2\)
The surface area of the cylinder with the diameter 2cm and height 15cm is \(100.48 \; cm^2\)
Learn more information about 'Surface area of cylinder' here
brainly.com/question/76387

which measurement is closest to the area of the shaded region in square inches

Answers
How to solve 2 and 1/2 divided by 3?
Answers
Answer: 5/6
Step-by-step explanation:
2 and 1/2 = 2.5
2.5 / 3 = 5/6 = 0.8333333
don't u have a calculator?