Answers
The range of the graphed function is y ≤ 1, or written in interval form, it is:
(-∞, 1]
What is the range of the function?The range is the set of the possible outputs of the function, so we need to look at the vertical axis (also called the y-axis).
Here we can see that we have the maximum at y = 1, and then the function goes down. (We can assume it will go to negative infinity, this is beacuse we can see arrow points at the ends, which means that the function keeps going downwards)
Then the range is:
y ≤ 1
Or (-∞, 1] in interval form.
Learn more about the range at:
https://brainly.com/question/10197594
#SPJ1
Related Questions
At a certain time of day, a 1.8-m-tall person standing next to the Washington
Monument casts a 0.7-m shadow. At the same time, the Washington Monument casts
a 65.8-m shadow. How tall is the Washington Monument?
Answers
Answer:
169.20 meters . hope it helps. I always write this when answer is in paper because it requires 20 alphabets minimum

graph the image of square abcdafter a translation 11 units left and 5 units up

Answers
Answer:
Explanation:
Here, we want to graph the new image of ABCD
What this means is that we get a new set of coordinates for each of the points
Let us look at the translation rule here, the rule is that the points move 11 units left and 5 units up
What that simply means is that we subtract 11 from the x-axis value, then add 5 to the y-axis value
We have that as follows:
A is (2,-8)
A' becomes (2-11, -8 + 5) which is (-9,-3)
B is (9,-8)
B' becomes (9-11, -8+5) which is (-2,-3)
C is (9,-1)
C' becomes (9-11 , -1+5) which is (-2,4)
D is (2,-1)
D' becomes (2-11,-1+5) which is (
which equation matches the graph?

Answers
Meaning, you plot (0,8) and move down 3 and right 1 for the slope.
Answer:
y=-3x+8
Step-by-step explanation:
Evaluate the integral. (remember to use absolute values where appropriate. use c for the constant of integration.
∫ √(x² + 2x)dx\
Answers
To evaluate the integral ∫ √(x² + 2x) dx, we can use the substitution method. By making a suitable substitution and performing the necessary calculations, we can find the antiderivative of the given function.
Let's start by making the substitution u = x + 1. This substitution helps simplify the expression under the square root.
Differentiating both sides with respect to x, we get du/dx = 1.
Rearranging the equation, we have dx = du.
Now, let's substitute the values in the integral:
∫ √(x² + 2x) dx = ∫ √(u²) du
= ∫ |u| du
= ∫ u du (since u is positive for the given range of x)
Integrating with respect to u, we have:
= (1/2) u² + c
Substituting back u = x + 1:
= (1/2) (x + 1)² + c
Therefore, the antiderivative of √(x² + 2x) is (1/2) (x + 1)² + c.
The absolute value is not necessary in this case since the expression inside the square root is always positive for the given range of x.
To learn more about antiderivative Click Here: brainly.com/question/30764807
#SPJ11
solve for X. 120=4x
Please help me!
Answers
Answer:
X=30
Step-by-step explanation:
1. Divide both sides by 4X to create zero pairs
2. 120/4= 30
Answer:
The answer is 30
Step-by-step explanation:
6-n=17 what does n equal im confused?
Answers
-So to find the variable all you have to do is move all the numbers to one side ( for instance move 6 to right side by subtracting from the left )
-n = 17- 6
-n = 11
- And now with your new equation ( -n = 11) move the negative sign it to the right side, which would give you
* n = -11
-To test it out just fill in the n with -11
6 - (- 11 ) = 17
Note ( negative X negative = a positive For example: { -2 x -3 = 6 }
- ( -11 ) = + 11
6 + 11 = 17
Making the equation of ( n = -11 ) correct!
Hope this helps you :)
Consider the following exponential probability density function. f(x) = 1/3 4 e^-x/3 for x > 0 a. Write the formula for P(x < x_0). b. Find P(x < 2). c. Find P(x > 3). d. Find P(x < 5). e. Find P(2 <.x <5).
Answers
The probability that x is less than 2 is approximately 0.4866. The probability that x is greater than 3 is approximately 0.3528. The probability that x is less than 5 is approximately 0.6321. The probability that x is between 2 and 5 is approximately 0.1455.
The given probability density function is an exponential distribution with a rate parameter of λ = 1/3. The formula for P(x < x_0) is the cumulative distribution function (CDF) of the exponential distribution, which is given by:
F(x_0) = ∫[0,x_0] f(x) dx = ∫[0,x_0] 1/3 * 4 * e^(-x/3) dx
a. Write the formula for P(x < x_0):
Using integration, we can solve this formula as follows:
F(x_0) = [-4e^(-x/3)] / 3 |[0,x_0]
= [-4e^(-x_0/3) + 4]/3
b. Find P(x < 2):
To find P(x < 2), we simply substitute x_0 = 2 in the above formula:
F(2) = [-4e^(-2/3) + 4]/3
≈ 0.4866
Therefore, the probability that x is less than 2 is approximately 0.4866.
c. Find P(x > 3):
To find P(x > 3), we can use the complement rule and subtract P(x < 3) from 1:
P(x > 3) = 1 - P(x < 3) = 1 - F(3)
= 1 - [-4e^(-1) + 4]/3
≈ 0.3528
Therefore, the probability that x is greater than 3 is approximately 0.3528.
d. Find P(x < 5):
To find P(x < 5), we simply substitute x_0 = 5 in the above formula:
F(5) = [-4e^(-5/3) + 4]/3
≈ 0.6321
Therefore, the probability that x is less than 5 is approximately 0.6321.
e. Find P(2 < x < 5):
To find P(2 < x < 5), we can use the CDF formula to find P(x < 5) and P(x < 2), and then subtract the latter from the former:
P(2 < x < 5) = P(x < 5) - P(x < 2)
= F(5) - F(2)
= [-4e^(-5/3) + 4]/3 - [-4e^(-2/3) + 4]/3
≈ 0.1455
Therefore, the probability that x is between 2 and 5 is approximately 0.1455.
To learn more about probability
https://brainly.com/question/30034780
#SPJ4
what is the probability that the lifetime of at least one component exceeds 2? (do not round intermediate values. round your answer to three decimal places.)
Answers
The probability that the lifetime of at least one component exceeds 2 is 0.135.
Given that the joint pdf is f(x,y)=xe^(-x(1+y)) for x≥0, y≥0 and 0 otherwise as shown in attached image.
We want to find the probability that the lifetime of at least one component exceeds 2.
The probability that the lifetime of at least one component exceeds 2 is P(X>2).
\(\begin{aligned}P(X > 2)&=\int_{x=2}^{\infty}\int_{y=0}^{\infty}f(x,y)dydx\end\)
Now, we will substitute the given function, we get
\(\begin{aligned}P(X > 2)&=\int_{x=2}^{\infty}\int_{y=0}^{\infty}xe^{-x(1+y)}dydx\end\)
Further, we will simplify this, we get
\(\begin{aligned}P(X > 2)&=\int_{x=2}^{\infty}\left[-e^{-x(1+y)\right]_{0}^{\infty}dx\\ &=\int_{x=2}^{\infty}e^{-x}dx\\ &=\left[-e^{-x}\right]_{2}^{\infty}\\ &=e^{-2}\\ &=0.135\end\)
Hence, the probability that the lifetime of at least one component exceeds 2 for the joint pdf is f(x,y)=xe^(-x(1+y)) for x≥0, y≥0 and 0 otherwise as shown in attached image is 0.135.
Learn more about the joint pdf from here brainly.com/question/15109814
#SPJ4

Find the magnitude of the
resultant vector.
(-25.6, 7.7)
(-11,-9.8)
Answers
To find the magnitude of the resultant vector, we need to first calculate the resultant vector itself. The resultant vector is the sum of the two given vectors (-25.6, 7.7) and (-11, -9.8). We can add these vectors by adding their corresponding components.
So, the x-component of the resultant vector is -25.6 - 11 = -36.6, and the y-component is 7.7 - 9.8 = -2.1. Therefore, the resultant vector is (-36.6, -2.1).
Now, to find the magnitude of this resultant vector, we use the Pythagorean theorem. The magnitude (or length) of a vector is given by the square root of the sum of the squares of its components. So,
magnitude of the resultant vector = sqrt((-36.6)^2 + (-2.1)^2)
= sqrt(1332.57 + 4.41)
= sqrt(1337.98)
= 36.6 (approximately)
Therefore, the magnitude of the resultant vector is 36.6 (approximately), and it is a vector that points in the direction (-36.6, -2.1).
It is important to note that vectors have both magnitude (length) and direction. In this case, we found the magnitude of the resultant vector, but we also know its direction. It is important to include both of these pieces of information when working with vectors.
To learn Pythagoras theorem, click here:
brainly.com/question/343682
#SPJ11
Find the remainder of 2338when divided by 55. b) What is the inverse of 23 modulo 55 i.e. which number a has the property that 23*a has the remainder 1 when divided by 55?
Answers
a) 2338 ≡ 42 • 55 + 28 ≡ 28 (mod 55)
b) We want to find a such that
23a ≡ 1 (mod 55)
Use the Euclidean algorithm:
55 = 2 • 23 + 9
23 = 2 • 9 + 4
9 = 2 • 4 + 1
⇒ 1 = 9 - 2 • 4
⇒ 1 = 9 - 2 • (23 - 2 • 9) = 5 • 9 - 2 • 23
⇒ 1 = 5 • (55 - 2 • 23) - 2 • 23 = 5 • 55 - 12 • 23
Solve for a :
5 • 55 - 12 • 23 ≡ 1 (mod 55)
⇒ -12 • 23 ≡ 1 (mod 55)
⇒ a ≡ -12 ≡ 43 (mod 55)
Please help 60 points for a rapid answer-In the figure below which of the following is true in circle E?


Answers
Answer:
all 3 options are true : A, B, C
Step-by-step explanation:
warning : it has come to my attention that some testing systems have an incorrect answer stored as right answer for this problem.
they say that A and C are correct.
but I am going to show you that if A and C are correct, then also B must be correct.
therefore, my given answer above is the actual correct answer (no matter what the test systems say).
originally the information about the alignment of the point F in relation to point E was missing.
therefore, I considered both options :
1. F is on the same vertical line as E.
2. F is not on the same vertical line as E.
because of optical reasons (and the - incomplete - expected correct answers of A and C confirm that) I used the 1. assumption for the provided answer :
the vertical line of EF is like a mirror between the left and the right half of the picture.
A is mirrored across the vertical line resulting in B. and vice versa.
the same for C and D.
this leads to the effect that all 3 given congruence relationships are true.
if we consider assumption 2, none of the 3 answer options could be true.
but if the assumptions are true, then all 3 options have to be true.
now, for the "why" :
remember what congruence means :
both shapes, after turning and rotating, can be laid on top of each other, and nothing "sticks out", they are covering each other perfectly.
for that to be possible, both shapes must have the same basic structure (like number of sides and vertices), both shapes must have the same side lengths and also equally sized angles.
so, when EF is a mirror, then each side is an exact copy of the other, just left/right being turned.
therefore, yes absolutely, CAD is congruent with CBD. and ACB is congruent to ADB.
but do you notice something ?
both mentioned triangles on the left side contain the side AC, and both triangles in the right side contain the side BD.
now, if the triangles are congruent, that means that each of the 3 sides must have an equally long corresponding side in the other triangle.
therefore, AC must be equal to BD.
and that means that AC is congruent to BD.
because lines have no other congruent criteria - only the lengths must be identical.
A research submarine dives at the rate of 6
feet every minute. What will the sub's
elevation be after 5 minutes of diving?
Which expression would describe this?
Answers
Y=5mins(let’s d number of elevation be y)
5x6=30
Y=30fts
A bycicle wheel whose radius is 30 cm covered distance in 70 revolutions how many km was the distance
Answers
Answer:
0.13188 km
Step-by-step explanation:
The distance covered by the bicycle wheel can be calculated using the formula:
distance = circumference x number of revolutions
The circumference of the wheel can be calculated using the formula:
circumference = 2 x pi x radius
where pi is approximately equal to 3.14.
Substituting the given values:
circumference = 2 x 3.14 x 30 cm
circumference = 188.4 cm
Now, we can calculate the distance covered by the wheel:
distance = circumference x number of revolutions
distance = 188.4 cm x 70
distance = 13188 cm
To convert this distance from centimeters to kilometers, we need to divide by 100,000 (since there are 100,000 centimeters in a kilometer):
distance = 13188 cm ÷ 100,000
distance = 0.13188 km
Therefore, the distance covered by the bicycle wheel is approximately 0.13188 km.
f(x1, x2) 421 +222 3x² +213 5x11² (√₁+√₂)² 10ln(₁) (x₁+x₂)(x² + x3) min(3r1, 10√2) max{5x1,2r2} MP1(x1, x₂) MP2(X1, X₂) TRS(x1, x₂) Output (2,4)
Answers
The given mathematical expression is evaluated for the input values (2, 4). The result of the expression is calculated using various operations such as addition, multiplication, square root, natural logarithm, minimum, maximum, and function composition.
The expression f(x1, x2) involves several mathematical operations. Let's evaluate each part of the expression step by step:
1. The first term is 421 + 222, which equals 643.
2. The second term is 3x² + 213. Plugging in x1 = 2 and x2 = 4, we get 3(2)² + 213 = 3(4) + 213 = 12 + 213 = 225.
3. The third term is 5x11². Substituting x1 = 2 and x2 = 4, we have 5(2)(11)² = 5(2)(121) = 1210.
4. The fourth term is (√₁+√₂)². Replacing x1 = 2 and x2 = 4, we obtain (√2 + √4)² = (1 + 2)² = 3² = 9.
5. The fifth term is 10ln(₁). Plugging in x1 = 2, we have 10ln(2) = 10 * 0.69314718 ≈ 6.9314718.
6. The sixth term is (x₁+x₂)(x² + x3). Substituting x1 = 2 and x2 = 4, we get (2 + 4)(2² + 4³) = 6(4 + 64) = 6(68) = 408.
7. The seventh term is min(3r1, 10√2). As we don't have the value of r1, we cannot determine the minimum between 3r1 and 10√2.
8. The eighth term is max{5x1,2r2}. Since we don't know the value of r2, we cannot find the maximum between 5x1 and 2r2.
9. Finally, we have MP1(x1, x2), MP2(X1, X2), and TRS(x1, x2), which are not defined or given.
Considering the given expression, the evaluated terms for the input values (2, 4) are as follows:
- 421 + 222 = 643
- 3x² + 213 = 225
- 5x11² = 1210
- (√₁+√₂)² = 9
- 10ln(₁) ≈ 6.9314718
- (x₁+x₂)(x² + x3) = 408
The terms involving min() and max() cannot be calculated without knowing the values of r1 and r2, respectively. Additionally, MP1(x1, x2), MP2(X1, X2), and TRS(x1, x2) are not defined.
To learn more about logarithm click here: brainly.com/question/30226560
#SPJ11
Perimeter Given Coordinates
Oct 15, 11:32:13 AM
The points E(7,-5), F(7, 2), G(4, 8), and H(4, 1) form parallelogram EFGH. Plot
he points then click the "Graph Quadrilateral" button. Then find the perimeter of the
parallelogram. Round your answer to the nearest tenth if necessary.
4
Answers
Perimeter of the parallelogram which points are E(7,-5), F(7, 2), G(4, 8), and H(4, 1) = 24 units.
There are 4 types of parallelograms, including 3 special types. The four types are parallelograms, squares, rectangles, and rhombuses.
A parallelogram is a shape with only two dimensions. It has four sides, two parallel pairs of which make up each side. The lengths of the parallel sides are also the same. The form is not a parallelogram if the lengths of the parallel sides are not equal.
Properties of parallelograms
Opposite sides are congruent (AB = DC).Opposite angels are congruent (D = B).Consecutive angles are supplementary (A + D = 180°).If one angle is right, then all angles are right.The diagonals of a parallelogram bisect each other.Given points are
E(7,-5),
F(7, 2),
G(4, 8), and
H(4, 1)
Perimeter of the parallelogram EFGH=2(EF+FG)
Distance between two points(x₁ , y₁) and (x₂ , y₂ ) can be calculated using the formula
√(x₂ - x₁ )² + (y₂ - y₁)²
Hence ,length of EF =
√(7 - 7 )² + (2 - (-5))²
=√49
=7units
And length of FG =
√(4 - 7 )² + (8 - 4)²
= √16 + 9
= √25
=5units
Hence, Perimeter of the parallelogram EFGH=2(EF+FG)=2(5+7)=24units
We have form parallelogram EFGH. For the result see the attachment-
To learn more about Parallelogram
https://brainly.com/question/20526916
#SPJ1

Answer:
27.4 units
Step-by-step explanation:
Given parallelogram EFGH with vertices E(7,-5), F(7, 2), G(4, 8), and H(4, 1), you want to know its perimeter.
Distance between two pointsThe distance between two points can be found from their coordinates using the distance formula ...
d = √((x2 -x1)² +(y2 -y1)²)
ApplicationThe distance between points F and G is ...
d = √((4 -7)² +(8 -2)²) = √(9 +36) = √45 ≈ 6.708
The distance between points E and F will be the difference of their y-coordinates:
d = √((7 -7)² +(2 -(-5))²) = √(0 +7²) = 7
PerimeterSince opposite sides of a parallelogram are the same length, the perimeter is twice the sum of two adjacent sides:
P = 2(EF +FG)
P = 2(7 +6.708) = 2(13.708) = 27.416
The perimeter of EFGH is about 27.4 units.
helpp
Plzzz
It’s
A
Question-
Steven earns extra money babysitting. He charges $29.00 for 4 hours and $50.75 for 7
hours.
Enter an equation to represent the relationship. Let x represent the number of hours
Steven babysits and y represent the amount he charges.
Answers
$50.00÷7hours=×$
$50.00÷7hours= 7.25
7.25 he charges per hour
get those points sis
Answers
Answer:
thanks
Step-by-step explanation:
find the value of y?

Answers
Step-by-step explanation:
Sum of angles in a quadrilateral = 360°.
=> y + 121° + 75° + 69° = 360°.
=> y = 95°.
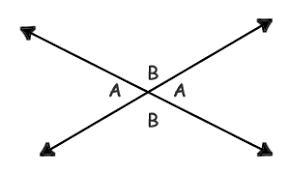
Verticle angles must have ?
Answers
Answer: Verticals angles are when 2 line intersect at a point forms 2 pairs of angles. The pairs will be opposite of each other.
The picture I have attached should give a good representation of what I mean.
The A angles are the same and the B angles are the same in the picture.
the graph of y=-3x+2, state the domain and the range
Answers
Answer:
Domain: (-∞,∞)
Range: (-∞, ∞)
Hope this helps.
2. MODELING REAL LIFE A dumpster rental fee is $350 for
the first week and $10 for each additional day or any portion
of a day. Write and graph a step function that represents the
cost y (in dollars) to rent the dumpster for x days.
Answers
The required function that represent the given situation is y = 10x + 350.
What is equation of line?In order to write the equation in y-intercept (y=mx+b) form and determine the equation of a graphed line, first determine the slope and y-intercept. The slope is the ratio of the y-to-x change. Find two locations on the line and create a sloping triangle connecting the two places.
According to question:Rental fee is $350 for the first week and $10 for each additional day or any portion of a day.
So, The equation that represent this problem is;
Let cost y (in dollars) to rent the dumpster for x days.
y = 350 + 10x (y in dollar)
y = 10x + 350
Here, slope of function is 10 and y- intersect is 350.
To know more about Equation of line visit:
brainly.com/question/21511618
#SPJ1
Where there is a jump at x = 7 from y = 350 to y = 350 + 10 * (x - 7). Before x = 7, the cost would remain constant at $350. After x = 7, the cost would increase by $10 for each additional day.
What is equation of line?In order to write the equation in y-intercept (y=mx+b) form and determine the equation of a graphed line, first determine the slope and y-intercept. The slope is the ratio of the y-to-x change. Find two locations on the line and create a sloping triangle connecting the two places.The step function representing the cost to rent the dumpster for x days can be defined as follows:y(x) = 350, if 0 < x <= 7y(x) = 350 + 10 * (x - 7), if x > 7The graph of this step function would look like a piecewise function, where there is a jump at x = 7 from y = 350 to y = 350 + 10 * (x - 7). Before x = 7, the cost would remain constant at $350. After x = 7, the cost would increase by $10 for each additional day.To learn more about Equation of line refer::
brainly.com/question/21511618
#SPJ1
* Ono 3 b) P and are the subsets of universal set U. If n (p) = 55% n (Q) = 50% and n(PUO)complement = 15% find: (i) n(PUQ) (ii) n(PDQ) (iii)n(only P) iv. n(only Q).
Answers
The probability of the sets are solved and
a) n(P U Q) = 85%
b) n(P ∩ Q) = 20%
c) n(only P) = 35%
d) n(only Q) = 30%
Given data ,
P and are the subsets of universal set U
And , n (p) = 55% n (Q) = 50% and n(PUO)complement = 15%
Now , we'll use the formula for the union and intersection of sets:
n(P U Q) = n(P) + n(Q) - n(P ∩ Q)
n(P ∩ Q) = n(P) + n(Q) - n(P U Q)
n(only P) = n(P) - n(P ∩ Q)
n(only Q) = n(Q) - n(P ∩ Q)
We're given that:
n(P) = 55%
n(Q) = 50%
n(P U Q)' = 15%
To find n(P U Q), we'll use the complement rule:
n(P U Q) = 100% - n(P U Q)'
n(P U Q) = 100% - 15%
n(P U Q) = 85%
Now we can substitute the values into the formulas above:
(i)
n(P U Q) = n(P) + n(Q) - n(P ∩ Q)
n(P ∩ Q) = n(P) + n(Q) - n(P U Q)
n(P ∩ Q) = 55% + 50% - 85%
n(P ∩ Q) = 20%
(ii)
n(P ∩ Q) = 20%
(iii) n(only P) = n(P) - n(P ∩ Q)
n(only P) = 55% - 20%
n(only P) = 35%
(iv)
n(only Q) = n(Q) - n(P ∩ Q)
n(only Q) = 50% - 20%
n(only Q) = 30%
Hence , the probability is solved
To learn more about probability click :
https://brainly.com/question/17089724
#SPJ1
becca repeatedly tosses a fair coin until she gets a heads, while daniel repeatedly rolls a fair six-sided die until he gets a 3 or higher. calculate the probability that the number of die rolls needed is greater than the number of coin tosses needed.
Answers
We need to roll a die at least 3 times and a coin should be tossed at least 2 times.
What is probability?Probability is the chance of occurrence of a certain event out of the total no. of events that can occur in a given context.
Given this, Becca repeatedly tosses a fair coin until she gets a head.
The probability of getting a head P(H) is = 1/2.
The probability of getting a number 3 or higher is,
P(3) + P(4) + P(5) + P(6).
= 1/6 + 1/6 + 1/6 + 1/6.
= 4/6.
= 2/3.
So, to get a number 3 or higher we need at least 3 rolls, and to get a head we need at least 2 tosses.
learn more about probability here :
https://brainly.com/question/743546
#SPJ1
write the symbolic expression for each of the following descriptions, then get rid of the radical and make them exponential expressions in fractional form. 11. the eighth root of fifty seven to the sixth degree
Answers
The final exponential expression in fractional form for "the eighth root of fifty-seven to the sixth degree" is 57^(3/4).
To express the given description as a symbolic expression and then convert it into an exponential expression in fractional form, we'll follow these steps:
Step 1: Symbolic Expression
The description states "the eighth root of fifty-seven to the sixth degree." Let's denote this as √[57]^(1/8)^6.
Step 2: Removing Radical
To eliminate the radical (√), we can rewrite it as a fractional exponent. The numerator of the fractional exponent corresponds to the power (6) applied to the base, and the denominator corresponds to the index of the root (8).
So, the expression becomes (57^(1/8))^6.
Step 3: Simplifying Exponents
To simplify the exponent, we multiply the powers:
(57^((1/8)*6))
Simplifying further:
(57^(6/8))
Step 4: Fractional Form
The exponent 6/8 can be simplified by dividing both the numerator and denominator by their greatest common divisor, which is 2:
(57^(3/4))
Therefore, the final exponential expression in fractional form for "the eighth root of fifty-seven to the sixth degree" is 57^(3/4).
This means that we raise 57 to the power of 3/4 to represent the original description. The fraction 3/4 indicates taking the eighth root of 57 and then raising it to the sixth power.
learn more about exponential expression here
https://brainly.com/question/26540624
#SPJ11
Solve the following equations. Show your answer on a number line.
|1/2-x/3|=5/6
Answers
Answer:
-1
Step-by-step explanation:
LCM is 6,after eliminating the fractions,you will arrive at 3-2x=5
-2x=5-3
-2x=2,divide both sides by -2x.
Sylvia is playing a game with a standard 6-sided number cube. If she rolls a 5 or more on both of her next turns, she will win the game. What’s the probability that this will happen? Express your answer as a fraction in simplest form.
Answers
Thus, the probability that Sylvia will toss 5 or more on the 6-sided number cube is found as: 1/3.
Explain about the probability?An event's probability is a numerical representation of how likely it is that the event will take place. This value is always in the range of 0 and 1, with 0 denoting impossibility and 1 denoting confidence. A fair coin flip with the two potential results being heads or tails is a classic illustration of a probabilistic experiment.
Given data:
6-sided number cube diced is rolled.sample space S = {1,2,3,4,5,6}Sample space for outcome as 5 and more S' = {5,6}As,
probability = favourable outcome / total outcome
probability(5 or more) = Sample space for outcome as 5 and more S' / sample space S
probability (5 or more) = 2/6 = 1/3
Thus, the probability that Sylvia will toss 5 or more on the 6-sided number cube is found as: 1/3.
know more about the probability
https://brainly.com/question/13604758
#SPJ1
3(-4+4)+5n=2n what are the steps for finding n
Answers
Answer:
1. Move the variables to one side: 3(-4+4) = -3n
2. Distribute. You will end up with 0 = -3n
3. Divide both sides by -3. n = 0
Step-by-step explanation:
Answer:
n=0
Step-by-step explanation:
3(-4+4)+5n=2n
first distribute
-12+12+5n=2n
combine like terms
5n=2n
subtract 2n on both sides
3n=0
divide by 3 on both sides
n=0/3
which is also equal to
n=0
For a continuous random variable x, the population mean and the population standard deviation are 148 and 9, respectively. You take a simple random sample of 36 elements from this population. The mean of the sampling distribution of the sample mean is:
Answers
Answer:
Step-by-step explanation:
The sample mean is an unbiased estimator of the population; therefore its mean across samples is 189.8. The standard error (defined as the standard deviation of these sample means) is 41.7 divided by the square root of 117, the sample size.
Find the number of ways you can dress if you have
5 pairs of shorts, six
T-shirts, and two pairs of shoes.
Answers
Answer: I think it’s 13
Step-by-step explanation:
Help asap worth 50 points
Use grouping symbols to make each equation true.
16-4/2+3=9
Answers
Answer:
This question is only if 25 points. And you have typed 50 points.
Answer is 16-4-2-1
16-4-2-1
Step-by-step explanation:
