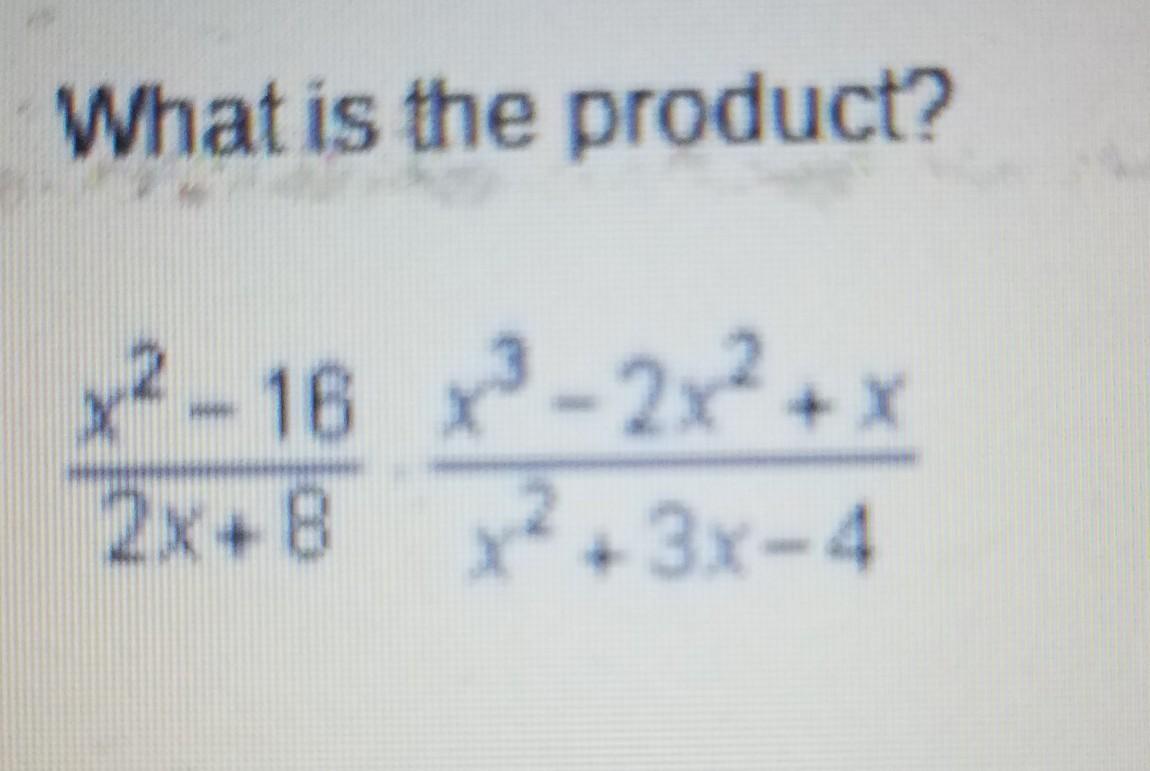What is the product?​

Answer:

|6n+7|=8=  n=1/6,-5/2

|3x–1|=4  x=5/3,-1

Step-by-step explanation:

Answer:

I think it would be the addition property of equality

Step-by-step explanation:

Population: All students in the high school.

Parameter of interest: Proportion of students whose names are known by the student body president.

learn more about proportion,

https://brainly.com/question/1496357

#SPJ11

Answer:

3

Step-by-step explanation:

Answer:

Step-by-step explanation:

3

The correct statement is the percent increase of her salary is 20% every year. Hence, the answer is option E. Given that a company's vice president's salary n years after becoming vice president is defined by the formula S(n) = 70000(1.2)". We have to determine which of the following statements is true:

Given that a company's vice president's salary n years after becoming vice president is defined by the formula S(n) = 70000(1.2)". We have to determine which of the following statements is true:

She will be receiving a 2% raise per year. Her salary will increase $14,000 every year. The percent increase of her salary is 120% every year. Her salary is always 0.2 times the previous year's salary. The percent increase of her salary is 20% every year.

To calculate the salary of the vice president after n years of becoming a vice president, we use the given formula:

S(n) = 70000(1.2)

S(n) = 84000

The salary of the vice president after one year of becoming a vice president: S(1) = 70000(1.2)

S(1) = 84000

The percent increase of her salary is: S(n) = 70000(1.2)n

S(n) - S(n-1) / S(n-1) × 100%

S(n) - S(n-1) / S(n-1) × 100% = (70000(1.2)n) - (70000(1.2)n-1) / (70000(1.2)n-1) × 100%

S(n) - S(n-1) / S(n-1) × 100% = 20%

Therefore, the correct statement is the percent increase of her salary is 20% every year. Hence, the answer is option E.

To know more about salary visit:

https://brainly.com/question/14371457

#SPJ11

The trigonometric ratio sine compares the lengths of the right triangle's two sides. Sin, though commonly abbreviated to sin, is actually pronounced sine.

To learn more about the sine triangle here

https://brainly.com/question/2920412

#SPJ4

the solution to the given difference equation is y(k) = \(0.2^k\) - 2.4 * \(1.2^k\)

To solve the given difference equation, we can use the Z-transform method. Let's denote the Z-transform of a function y(k) as Y(z), and the Z-transform of x(k) as X(z).

Applying the Z-transform to the given equation and using the properties of linearity, time shifting, and the Z-transform of the unit step function, we have:

z²Y(z) - zY(z) + 0.24Y(z) = (z + 1)X(z)

Next, we can rearrange the equation to solve for Y(z):

Y(z)(z² - z + 0.24) = (z + 1)X(z)

Dividing both sides by (z² - z + 0.24), we get:

Y(z) = (z + 1)X(z) / (z² - z + 0.24)

Now, we need to find the inverse Z-transform of Y(z) to obtain the time-domain solution y(k). To do this, we can use partial fraction decomposition and lookup tables to find the inverse Z-transform.

The denominator of Y(z), z² - z + 0.24, can be factored as (z - 0.2)(z - 1.2). We can then rewrite Y(z) as:

Y(z) = (z + 1)X(z) / [(z - 0.2)(z - 1.2)]

Now, we perform partial fraction decomposition to express Y(z) as:

Y(z) = A / (z - 0.2) + B / (z - 1.2)

To find the values of A and B, we can multiply both sides of the equation by the common denominator:

(z - 0.2)(z - 1.2)Y(z) = A(z - 1.2) + B(z - 0.2)

Expanding and equating coefficients, we have:

z²Y(z) - 1.4zY(z) + 0.24Y(z) = Az - 1.2A + Bz - 0.2B

Now, we can equate the coefficients of corresponding powers of z:

Coefficient of z²: 1 = A

Coefficient of z: -1.4 = A + B

Coefficient of z⁰ (constant term): 0.24 = -1.2A - 0.2B

Solving these equations, we find A = 1, B = -2.4.

Substituting these values back into the partial fraction decomposition equation, we have:

Y(z) = 1 / (z - 0.2) - 2.4 / (z - 1.2)

Now, we can use the inverse Z-transform lookup tables to find the inverse Z-transform of Y(z):

y(k) = Z⁻¹{Y(z)} = Z⁻¹{1 / (z - 0.2) - 2.4 / (z - 1.2)}

The inverse Z-transform of 1 / (z - 0.2) is given by the formula:

Z⁻¹{1 / (z - a)} = \(a^k\)

Using this formula, we get:

y(k) = \(0.2^k\) - 2.4 * \(1.2^k\)

Therefore, the solution to the given difference equation is y(k) = \(0.2^k\) - 2.4 * \(1.2^k\)

Learn more about Z-transform method here

https://brainly.com/question/14979001

#SPJ4

The surface area of the baseball is 176.6 cm² b.

To find the surface area of the baseball:

  r=3.75

\(A=4\pi r^{2}\)

\(A=4*\pi *3.75^{2}\)

A=176.6 cm² b.

The surface area of the baseball is 176.6 cm² b.

To learn more about surface area, refer to:

https://brainly.com/question/1297098

#SPJ4

The X value corresponding to z = -2.00 is 60. The X value corresponding to z = -2.00 is 60. This means that the observation with a z-score of -2.00 is 60 units below the population mean of 80.

To find the X value corresponding to z = -2.00, we can use the formula:
z = (X - µ) / σ
Substituting the given values, we get:
-2.00 = (X - 80) / 10
Solving for X, we get:
X = (-2.00 x 10) + 80
X = 60

The z-score measures the number of standard deviations an observation is from the mean. In this case, the given z-score of -2.00 indicates that the observation is 2 standard deviations below the mean.
To find the corresponding X value, we use the formula:
z = (X - µ) / σ
Where z is the standard normal distribution value, X is the corresponding raw score, µ is the mean of the population, and σ is the standard deviation of the population.
Substituting the given values, we get:
-2.00 = (X - 80) / 10
Solving for X, we get:
X = (-2.00 x 10) + 80
X = 60

To know more about population mean visit :-

https://brainly.com/question/30324262

#SPJ11

In this question, the z-score associated with the 97.5 percent confidence interval is option e) 1.960.

In statistics, the z-score is used to determine the number of standard deviations a particular value is away from the mean in a normal distribution. The z-score is commonly used in confidence interval calculations, where it corresponds to a certain level of confidence.

The 97.5 percent confidence interval corresponds to a two-tailed test, meaning we need to find the z-score that captures 97.5 percent of the area under the normal distribution curve, with 2.5 percent of the area in each tail.

Looking up the z-score in a standard normal distribution table or using statistical software, we find that the z-score associated with the 97.5 percent confidence interval is approximately 1.960.

Therefore, the correct answer is e) 1.960. This z-score is used when constructing a 97.5 percent confidence interval, which means there is a 97.5 percent probability that the true population parameter lies within the interval calculated using this z-score.

Learn more about z-score here:

brainly.com/question/31871890

#SPJ11

Answer: Assume π = 3.14(rounded upto two decimal point)

Case I. 1 year = 365 days

2 years = 730 days

3 years = 1095 days

And .14 years = 51 days 2 hours 24 minutes

So, 3.14 years = 1146 days 2 hours 24 minuts.

Now, suppose you born in a leap-year.

Case II. 1 year = 366 days

2 years = 732 days

3 years = 1098 days

and .14 years = 51 days 5 hours 45 minutes 36 seconds

Then, 3.14 years = 1149 days 5 hours 45 minuts 36 seconds

So, yes, it is possible to be exactly π years old. At exactly 1146 days 2 hours 24 minutes or 1149 days 5 hours 45 minutes 36 seconds (in case of a leap-year born), we could have celebrate at our π years birthday.

Step-by-step explanation:

Answer:

x = 10.8

Step-by-step explanation:

9 ÷ x = x ÷ (9 + 4)

9 × (9 + 4) = x × x

9 × 13 = x²

117 = x²

x = 10.81665383

Answer:

(-1, -3) and (1, 1)

Step-by-step explanation:

Use a graphing calculator to graph out both lines:

(See picture)

Both lines intersect at points (-1, -3) and (1, 1). These are the solutions for the system of equations.

Answer:

Step-by-step explanation:

The number of real solution of a quadratic equation can be found from the number of x-intercepts on the graph. If the curve passes through the x-axis twice, (2 x-intercepts), then the equation has two real solutions.

If it passes through once, (the vertex is on x-axis), then there is one real solution, and if it does not touch the x-axis at all (floating above it or below it), then it has no real solutions.

Hope this helped!

The range of the function f(x) = log5x is (-∞, +∞).The function f(x) = log5x represents the logarithm base 5 of x. To determine the range of this function, we need to consider the possible values that the logarithm can take.

The range of the logarithm function y = log5x consists of all real numbers. The logarithm function is defined for positive real numbers, and as x approaches 0 from the positive side, the logarithm approaches negative infinity. As x increases, the logarithm function approaches positive infinity.

The range of the function is the set of all possible output values. In this case, the range consists of all real numbers that can be obtained by evaluating the logarithm

log5(�)log 5 (x) for �>0 x>0.

Since the base of the logarithm is 5, the function log5x will take on all real values from negative infinity to positive infinity. Therefore, the range of the function f(x) = log5x is (-∞, +∞).

In other words, the function can output any real number, ranging from negative infinity to positive infinity. It does not have any restrictions on the possible values of its output.

For more such questions on Logarithm:

https://brainly.com/question/31117877

#SPJ8

Answer: All real numbers

Step-by-step explanation:

Edge

The rectangle's area is decreasing at a rate of 40 square meters per day when the length is 10 meters and the width is 18 meters.

We have to find the rate of change of area of the rectangle, that is, dA/dt.

Let L be the length and W be the width of the rectangle.

So, the area of the rectangle, A = L * W

Now, when the length is 10m and width is 18m,

then A = L * W

= 10 * 18

= 180 sq. meters

Differentiating both sides of A = L * W with respect to time, t, we get:

dA/dt = d/dt (L * W)

On applying product rule of differentiation, we get:

dA/dt = (dL/dt) * W + L * (dW/dt)

We know that dL/dt = -5 (given: The length of a rectangle is decreasing at a rate of 5 meters per day)

and dW/dt = 5 (given: the width is increasing at a rate of 5 meters per day).

So, dA/dt = (-5) * 18 + 10 * 5

= -90 + 50

= -40 square meters per day.

Learn more about area  -

brainly.com/question/2607596

#SPJ11

Answer:

In mathematics education, precalculus or College algebra is a course, or a set of courses, that includes algebra and trigonometry at a level which is designed to prepare students for the study of calculus. Schools often distinguish between algebra and trigonometry as two separate parts of the coursework.

Step-by-step explanation:

Dude you can search this stuff up

The sine function is: 8.25 sin (0.25t) + 2

Let the diameter of the Ferris wheel be D = 16.5 m

The radius of the Ferris wheel is given by R = D/2 = 8.25 m

If t is the time in seconds, the angular velocity ω in radians per second is given by the formula ω = θ / t where θ is the angular displacement in radians.

Given, the angular velocity ω = 0.25 rad/s

The period of rotation is given by the formula T = 2π / ω where T is the time taken to complete one revolution.

So, T = 2π / 0.25 = 8π seconds.

Now, we can write the equation for the height of the car above the ground as a function of time t as follows:

Let h be the height of the car relative to the ground as a function of the time t in seconds.

Then we have;h = R sin (θ) + 2

where θ is the angular displacement of the car from its lowest position.

The maximum height occurs when the car is at the top of the Ferris wheel.

At the top, θ = π / 2 and so;h(max) = R sin (π / 2) + 2 = R + 2 = 10.25 meters.

Substituting the values R = 8.25 and T = 8π seconds in the equation for θ we have;θ = ωt = 0.25t radians.

Now we can substitute this value of θ in the equation for h to get the height of the car above the ground at any given time t.

Therefore;h = 8.25 sin (0.25t) + 2 meters. Answer: 8.25 sin (0.25t) + 2

Know more about sine function here:

https://brainly.com/question/21902442

#SPJ11

There would be 3 linear coefficients (one for each original variable), 3 quadratic coefficients (one for each squared original variable), and 4 interaction coefficients (one for each unique combination of two original variables).

If there are 3 original predictor variables, and we want to create a quadratic regression model, we would need to include the square terms of each of the original variables, as well as the interaction terms between the variables.

This would result in a total of 10 coefficients, including the intercept term.

Specifically, there would be 3 linear coefficients (one for each original variable), 3 quadratic coefficients (one for each squared original variable), and 4 interaction coefficients (one for each unique combination of two original variables).

To know more about linear coefficients refer here

https://brainly.com/question/30930123#

#SPJ11

Answer:

line ML are parallel to line OP

Step-by-step explanation:

To find the component form of the velocity of the airplane, we need to resolve the velocity vector into its horizontal and vertical components.

Assuming that the bearing of 110 degrees is measured clockwise from the North, the horizontal component of the velocity is given by:

cos(110 degrees) = -sin(20 degrees) ≈ -0.342

Horizontal component = 560 mph * (-0.342) ≈ -191.5 mph

Similarly, the vertical component of the velocity is given by:

sin(110 degrees) = cos(20 degrees) ≈ 0.940

Vertical component = 560 mph * 0.940 ≈ 526.4 mph

Therefore, the component form of the velocity of the airplane is approximately (-191.5 mph, 526.4 mph).

Answer:

Like any constant value, the value 0 can be considered as a (constant) polynomial, called the zero polynomial. It has no nonzero terms, and so, strictly speaking, it has no degree either. As such, its degree is usually undefined.

Step-by-step explanation:

Answer:

True

Step-by-step explanation:

Answer:

A lower price and quantity would result.

The expression \((x+4)(x^2+x-2)\) in standard form is\(x^3 + 5x^2 + 2x - 8.\) Standard form refers to arranging the terms in descending order of exponents, with the highest degree term appearing first, followed by the lower degree terms. The expression above is in standard form as the terms are arranged in descending order of their degree:\(x^3, 5x^2, 2x,\)and the constant term -8.

To write the expression\((x+4)(x^2+x-2)\) in standard form, we need to simplify and combine like terms.

First, we will use the distributive property to multiply the terms:

\((x+4)(x^2+x-2) = x(x^2+x-2) + 4(x^2+x-2)\)

Now, we multiply each term individually:

\(x(x^2) + x(x) + x(-2) + 4(x^2) + 4(x) + 4(-2)\)

Simplifying further, we get:

\(x^3 + x^2 - 2x + 4x^2 + 4x - 8\)

Combining like terms, we can add the coefficients of the same degree terms:

\(x^3 + (x^2 + 4x^2) + (-2x + 4x) - 8\)

This simplifies to:

\(x^3 + 5x^2 + 2x - 8\)

For more such questions on standard forms

https://brainly.com/question/19169731

#SPJ8

Step-by-step explanation:

Move -5 to the left of f. -5f

The minimum value of C is 14 because the inequality x + 3y ≥ 14 has the minimum value is 14.

It is defined as the expression in mathematics in which both sides are not equal they have mathematical signs either less than or greater than, known as inequality.

Given that,

C = x + 3y

Subject to constraints:

9x + 2y > 35

x + 3y ≥ 14

X ≥ 0

y ≥  0

As we can see in the inequality:

x + 3y ≥ 14

Compare with x + 3y = C

The minimum value of x + 3y is 14

Thus, the minimum value of C is 14 because the inequality x + 3y ≥ 14 has the minimum value is 14.

Learn more about the inequality here:

brainly.com/question/19491153

#SPJ1

Answer:

1 : 2.56

Step-by-step explanation:

Since the sign and the banner are similar, their ratio of length to width should be the same. Hence, 32/45 = 20/x, with x being the width of the school banner.

32/45 = 20/x

32x = 20*45

x = 900/32

x = 28.125 inches

Now, we can calculate the area of the school banner and the sign:

Area of school banner:

28.125 * 20 = 562.5 square inches

Area of sign:

32 * 45 = 1440 square inches

Hence, the ratio of the area of banner to the area of sign is:

562.5 : 1440

1 : 2.56

Hope this helped!

Answer:

1 : 2.56

Step-by-step explanation:

plz mark brainly

Answer:

387

Step-by-step explanation:

Answer:

387

Step-by-step explanation:

13+5

18*21

378+9

=387

Answer:

95 points

Step-by-step explanation:

Let P = Big Town's points

5/2 = P/38

2P = 190

P = 95 points