What is the pascal’s theory?
Answers
PLEASE GIVE ME BRAINLIEST!
i hope this helps. thank you and have a good day :)
Answer:
a principle in fluid mechanics that states that when there is an increase in pressure at any point in a confined fluid, there is an equal increase at every other point in the container.
Step-by-step explanation:
pressure applied to a fluid is transmitted equally throughout the fluid in all directions. This is named after the French mathematician and physicist Blaise Pascal, who first formulated it in the mid-17th century.
Related Questions
the hcf of 12x^2-4xy+15x-5y
Answers
Answer:
-1
Step-by-step explanation:
We have 2 letters, x and y. what letter is in all of them? none of them. that means the HCF can't contain a letter. let's take away the letters, we have 12, -4, 15, -5. Since -5 is a prime number. the answer is -1
Which division problem would have an estimated quotient of 15 if the divisor and dividend were rounded to the nearest whole number? What is the right option?
Answers
Answer:
90.24 divided by 6.3
Step-by-step explanation:
For reaching to the answer, we have to test each of the options given
The first option says that the divisor and dividend is 90.24 and dividend is 6.3
Now if we rounded it
So it would be 90 and 6
So, the quotient is
= 90 ÷ 6
= 15
Hence, the first option is correct
i.e. 90.24 divided by 6.3
And, all the other options are wrong
Solve: 4|x| = 32
–8 or 8
8
24
no solution
Answers
Answer:
-8 or 8
Step-by-step explanation:
We are given the absolute equation:
\(\displaystyle \large{4|x|=32}\)
First, divide both sides by 4 which leaves \(\displaystyle \large{|x|=8}\)
Absolute Value Definition
\(\displaystyle \large{|x|=\begin{cases} x \ \ \ (x\geq 0)\\ -x \ \ \ (x<0) \end{cases}}\)
So from |x| = 8, break into two intervals/conditions.
(1) when x ≥ 0
x = 8
(2) when x < 0
-x = 8
x = -8
From (1) and (2), the solution to 4|x| = 32 is 8 or -8
Solve the equation for y.
4x = -2y
A. y= 1/2x + 2
B. y= -1/2x
C. Y= -2x
D. y = x + 2
Answers
Answer:
Answer is C...........................
Step-by-step explanation:
Answer:
C.) y = -2x
Step-by-step explanation:
To solve for y, u gotta divide both sides by -2 to get y by itself. When u do that, u get -2x.
The salary of college professors from more than 25,000 universities and colleges in USA is normally distributed with a mean, $85,900 and its standard deviation, $11,000. If you collect a random sample from 35 professors, find the probability that the sample mean is between $70,000 and $100,000?
Answers
Answer:
The answer is below
Step-by-step explanation:
The z score is used to determine by how many standard deviations the raw score is above or below the mean. The z score is given by the formula:
\(z=\frac{x-\mu}{\sigma} \\\\where\ x=raw\ score,\mean,\ \sigma=standard\ deviation.\\\\For \ a\ sample\ size(n):\\\\z=\frac{x-\mu}{\sigma/\sqrt{n} }\)
Therefore given that μ = $85900, σ = $11000, n = 35.
For x > 70000:
\(z=\frac{x-\mu}{\sigma/\sqrt{n} } =\frac{70000-85900}{11000/\sqrt{35} } =-8.55\\\)
For x < 100000
\(z=\frac{x-\mu}{\sigma/\sqrt{n} } =\frac{100000-85900}{11000/\sqrt{35} } =7.58\)
From the normal distribution table, P(70000< x < 100000) = P(-8.55 < z < 7.58) = P(z < 7.58) - P(z < -8.55) = 1 - 0 = 1 = 100%
2.1Simplifying Expressions: Problem 1 (1 point) Simplify the following expression. 6- 4(x - 5)-
Answers
The simplified expression is 26 - 4x.
To simplify the expression 6 - 4(x - 5), we can apply the distributive property and simplify the terms.
6 - 4(x - 5)
First, distribute -4 to the terms inside the parentheses:
6 - 4x + 20
Now, combine like terms:
(6 + 20) - 4x
Simplifying further:
26 - 4x
Therefore, the simplified expression is 26 - 4x.
Learn more about distributive property here
https://brainly.com/question/12192455
#SPJ11
\(\sf 10\times 5\times 11\)
Answers
Answer:
\(\sf\longmapsto \: 550\)
Step-by-step explanation:
\(\sf\longmapsto \: 50 \times 11\)
\(\sf\longmapsto \: 550\)
Answer:
\(\sf 550\)
Step-by-step explanation:
\(10 \times 5 = 50 \\ \)
\(50 \times 11 = 550\)
If P(-9, -4), Q(-7, -1), R(-2, 5), S(-6, -1) are the coordinates of the points, what is the slope of line PQ?
Answers
Given :
P(-9, -4), Q(-7, -1), R(-2, 5), S(-6, -1).
To Find :
The slope of line PQ.
Solution :
We know , slope is given by :
\(m=\dfrac{y_2-y_1}{x_2-x_1}\\\\m=\dfrac{-9-(-7)}{-4-(-1)}\\\\m=\dfrac{2}{3}\)
Therefore, the slope of line PQ is 2/3.
Hence, this is the required solution.
The radius of Cylinder A measures ____ feet.
14, 7, 10
The radius of Cylinder B measures ____ feet.
1.4, 2.8, 5.7

Answers
Answer:
The radius of Cylinder A measures 7 feet.
The radius of Cylinder B measures 2.8 feet.
Step-by-step explanation:
The radius of Cylinder A measures 7 feet.
because the radious is half of the diameter and 14 is the diameter
The radius of Cylinder B measures 2.8 feet.
Answer:
Cylinder A's radius is 7 because the radius is diameter divided by 2.
Cylinder B's radius is 2.8 because the height of Cylinder A is 5 times bigger than Cylinder B's height.
Step-by-step explanation:
A shipping container will be used to transport several 120-kilogram crates across the country by rail. The greatest weight that can be loaded into the container is 27500 kilograms. Other shipments weighing 12400 kilograms have already been loaded into the container. Which inequality can be used to determine x, the greatest number of
120-kilogram crates that can be loaded onto the shipping container?
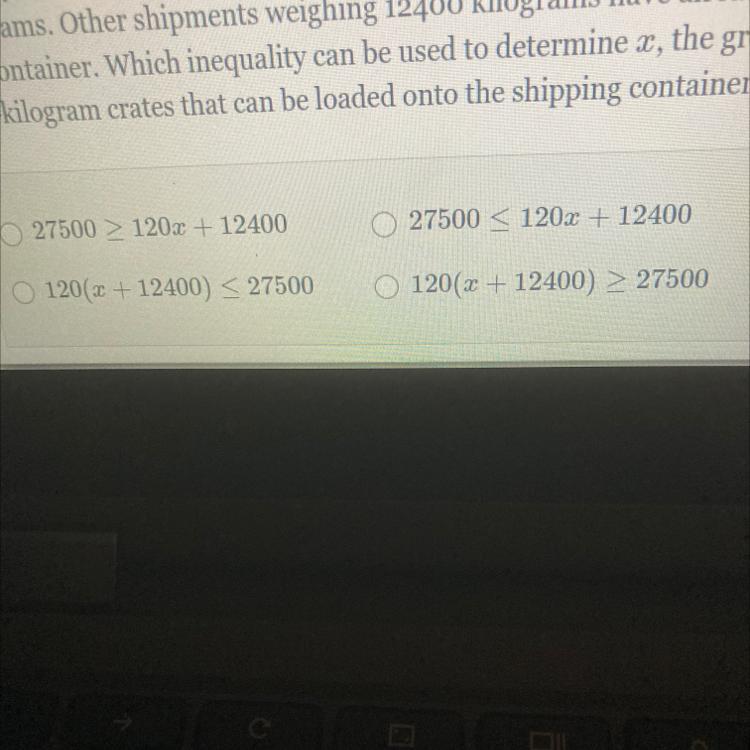
Answers
Inequality can be used to determine x, the greatest number of 120-kilogram crates that can be loaded onto the shipping container is 8000 + 120C <= 27500
What is inequality?An inequality is a relationship that allows us to contrast two or more mathematical expressions.
Knowing that;
Each carton weighs 120 kg.
The container's maximum weight when loaded is 27500 kg.
Weight of the container as it is currently loaded: 8000 kg
Now that we have merged, we have;
Solution
because 8000 grams have already been loaded kilograms
into the container
each crate weighs 120 kilograms.
so 8000 + 120C <= 27500
To learn more about inequality refer to:
https://brainly.com/question/28862943
#SPJ1
Suppose the radius of a cylinder changes, but its volume stays the same. How must the height of the cylinder change?
h
The height does not change.
If the radius increases, then the height must increase
9
If the ladus decreases, then the height must decrease

Answers
If the volume of a cylinder stays the same while the radius changes, the height of the cylinder must change inversely with the radius.
We have,
If the volume of a cylinder stays the same while the radius changes, the height of the cylinder must change inversely with the radius.
This means,
If the radius increases, the height must decrease to compensate and keep the volume constant.
If the radius decreases, the height must increase to compensate and maintain the same volume.
This relationship is due to the formula for the volume of a cylinder, which involves both the radius and the height.
By adjusting one variable (radius) while keeping the volume constant, the other variable (height) must change accordingly to maintain the balance.
Thus,
If the volume of a cylinder stays the same while the radius changes, the height of the cylinder must change inversely with the radius.
Learn more about cylinder here:
https://brainly.com/question/15891031
#SPJ1
The rectangular
base of a
20ft tall storage unit is shown
below. Which statement is
FALSE?
a)
b)
c)
The area of the
base is 30ft²
The area is 26ft²
The perimeter is
26ft
d) The perimeter is
(3+3)+(10+10)
MD
Th
3ft
Oft
Answers
Answer:
The statement that is FALSE is b) "The area is 26ft²".
0
Given that the triangles are similar, find the value of x. Find the length of NR.
S
T
40
60
R
2x-2
8
N
M
X=
NR =

Answers
Answer:
NR = 12
Step-by-step explanation:
Given that both trjangles are similar, therefore, it follows that their corresponding side lengths would be proportional to each other. Thus:
\( \frac{40}{8} = \frac{60}{2x - 2} \)
\( 5 = \frac{60}{2x - 2} \)
Cross multiply
\( 5(2x - 2) = 60 \)
\( 10x - 10 = 60 \)
\( 10x = 60 + 10 \) (addition property of equality)
\( 10x = 70 \)
Divide both sides by 10
x = 7
✔️NR = 2x - 2
Plug in the value of x
NR = 2(7) - 2 = 14 - 2
NR = 12
which distance metric would best describe this: how far apart
are two binary vectors of the same length ? justify your
answer?
Answers
The Hamming distance metric is the best metric for describing how far apart two binary vectors of the same length are. The reason for this is that the Hamming distance is a measure of the difference between two strings of the same length.
Its value is the number of positions in which two corresponding symbols differ.To compute the Hamming distance, two binary strings of the same length are compared by comparing their corresponding symbols at each position and counting the number of positions at which they differ.
The Hamming distance is used in error-correcting codes, cryptography, and other applications. Therefore, the Hamming distance metric is the best for this particular question.
To know more about distance refer here :
https://brainly.com/question/13034462#
#SPJ11
Which of these is a correct expansion of (3x – 2)(2x2 + 5)?
A. 3x • 2x2 + 3x • 5 + (–2) • 2x2 + (–2) • 5
B. 3x • 2x2 + 3x • 5 + 2 • 2x2 + 2 • 5
C. 3x • 2x2 + (–2) • 2x2 + 2x2 • 5 + (–2) • 5
Answers
The correct expansion of (3x – 2)(2\(x^2\) + 5) is 3x • 2\(x^2\) + 3x • 5 + (–2) • 2\(x^2\) + (–2) • 5. Thus, option A is the right answer to the given question.
To expand an expression of multiplication of two variables to two variables is done as follows:
1. We take the first term of the first expression which in this case is 3x
2. We multiply it by the first term of the second expression. In this case, we get 3x • 2\(x^2\).
3. Subsequently we multiply the first term with further terms and add them. In the given case, the expression we get is 3x • 2\(x^2\) + 3x • 5
4. Then we take the second term of the first expression and repeat the above steps and add it to the existing equation.
We get x • 2\(x^2\) + 3x • 5 + (–2) • 2\(x^2\) + (–2) • 5 as the answer.
Learn more about Expressions:
brainly.com/question/25968875
#SPJ4
A biker cycles 9 miles in 2 3 of an hour. b The distance here varies directly with time. What is the constant of variation? (It is the hikers’ rate .)
Answers
Answer:
27/2
Step-by-step explanation:
Hope this helps! Also dont add comments to get gems like bruh ;-;
Answer: 27/2
Step-by-step explanation:
\(9\cdot \:1=x\frac{2}{3}\)
\(x\frac{2}{3}=9\cdot \:1\)
\(x\frac{2}{3}=9\)
\(3x\frac{2}{3}=9\cdot \:3\)
2x= 27
x= 27/2
Add Me Brainliest!
If 33% of a man monthly salary is Birr of 6600, what is his total monthly salary? A. 23,200 B. 20,000 C. 9,850 D. 16,450
Answers
Answer:
The correct answer is B. 20,000
Step-by-step explanation:
To determine the man's total monthly salary, we can set up a simple equation using the given information. Let's denote the total monthly salary as "x."
According to the information provided, 33% of the man's monthly salary is equal to Birr 6600. We can express this relationship mathematically as:
0.33x = 6600
To solve for "x," we need to isolate it on one side of the equation. We can do this by dividing both sides of the equation by 0.33:
x = 6600 / 0.33
Evaluating the right side of the equation gives:
x ≈ 20,000
Therefore, the man's total monthly salary is approximately Birr 20,000.
Hence, the correct answer is B. 20,000.
g is most data likely to be skewed or symmetric? there is no right or wrong here but discuss and take a side on the issue.
Answers
Most data is likely to be skewed following a particular trait because when considering real life data, it is likely that it may concentrate on one end of the values on the real line as there is high uncertainty that exists with real life.
There is very little confidence that the population would behave in expected ways.
The skewed distribution implies the distribution that is not symmetrical. If a distribution is skewed it can be skewed to the left i.e. mean lies to the left of the center or skewed to the right i.e. mean lies to the right of the center of the distribution.
To know more about Real life data, visit: brainly.com/question/28193706
#SPJ4
A psychology student conducted a survey and the results indicate that regular exercise leads to weight loss. The student used this conclusion in his recent paper. What could be wrong with this conclusion
Answers
The conclusion that regular exercise leads to weight loss, based solely on the results of a survey, may have several potential flaws.
It is important to consider potential issues with the conclusion drawn from the survey results. First, the survey itself may suffer from limitations such as sampling bias or self-reporting biases. The sample of participants in the survey may not be representative of the general population, leading to inaccurate or skewed results. Additionally, relying on self-reported data about exercise and weight loss introduces the possibility of response bias or inaccuracies in reporting.
Other factors, such as dietary habits, genetics, or underlying health conditions, could contribute to weight loss alongside exercise. Without controlling for these factors or conducting a more rigorous study design, it is challenging to establish a direct causal relationship between regular exercise and weight loss.
Learn more about factors here:
https://brainly.com/question/14549998
#SPJ11
22. The first 5 terms of a number pattern are shown below.
4, 9, 14, 19, 24,
Which expression is equivalent to the value of the nth term in the pattern?
5n -1
57
n +5
5n +3
Answers
the patterns going up in 5s and to get back to 4 you need to - 1
The expression is equivalent to the value of the nth term in the pattern is aₙ = 5n - 1. Then the correct option is A.
What is an arithmetic sequence?Let a₁ be the first term and d be a common difference. Then the nth term of the arithmetic sequence is given as,
aₙ = a₁ + (n - 1)d
The first 5 terms of a number pattern are shown below.
4, 9, 14, 19, 24
The first term of the sequence is 4 and the common difference between the terms is given as,
d = 9 - 4
d = 5
The expression is equivalent to the value of the nth term in the pattern and will be
aₙ = 4 + (n - 1) x 5
aₙ = 4 + 5n - 5
aₙ = 5n - 1
The expression is equivalent to the value of the nth term in the pattern is aₙ = 5n - 1. Then the correct option is A.
More about the arithmetic sequence link is given below.
https://brainly.com/question/12373434
#SPJ5
Next, the team wants to explore how it can change the steepness of the curved pit.
Identify how the graph of each equation compares with the graph of the parent quadratic equation, y = x2.
Drag the equations to the correct location on the chart. Not all equations will be used.

Answers
Given that the parent function, y = x², has a leading coefficient of 1, the
following are the comparisons of the equations with the parent functions;
\(\begin{array}{|c|cc|}Steeper \, than \, y = x^2&&Less \, Steep \ than \, y = x^2 \\y = 2 \cdot x^2&&y = \frac{1}{2} \cdot x^2 \\y = \left(2 \cdot x \right)^2&&y = \left(\frac{1}{2} \cdot x \right)^2 \end{array}\right]\)
How can the correct location of each equation be found?The parent function is y = x²
The leading coefficient of the parent function = 1
The steepness of a quadratic equation is given by the value of the
leading coefficient.
When the leading coefficient is larger than 1, we have;
The function is steeper than y = x²
When the leading coefficient is a fraction larger than 0 but lesser than 1, we have;
The function is less steep than y = x²
Which gives;
\(\begin{array}{|c|cc|}Steeper \, than \, y = x^2&&Less \, Steep \ than \, y = x^2 \\y = 2 \cdot x^2&&y = \frac{1}{2} \cdot x^2 \\y = \left(2 \cdot x \right)^2&&y = \left(\frac{1}{2} \cdot x \right)^2 \end{array}\right]\)
The function y = -x² is inverted has the same steepness as y = x², but will not be used.
Learn more about the properties of quadratic functions here:
https://brainly.com/question/10989920
use the counting principle to determine the number of elements in the sample space. the possible ways to complete a multiple-choice test consisting of 24 questions, with each question having four possible answers (a, b, c, or d).
Answers
There are 4²⁴ possible ways to complete the multiple-choice test consisting of 24 questions, with each question having four possible answers.
We have 24 questions with each having 4 possible outcomes. If we had a question, then we would have 4 ways of answering question 1 and for each of the four answers in question 1, we would have four ways of answering question 2. So, we have 4² ways of answering the questions.
Like this, we have 24 questions. There are four ways to choose an answer to each question. By counting principle, we multiply the number of choices at each step and then we have -
= 4×4×4×4...= 4²⁴ ways to complete the test
Learn to know more about the counting principle on
https://brainly.com/question/10275154?referrer=searchResults
#SPJ4
Help me out with this question!! 50 points

Answers
C
The mistake the arrangers made is in the second inequality. They considered the number of caps to be bought should be at least 5 times greater than the number of blouses, not the other way around. The correct inequality should be C
The correct answer is D) The first inequality should be s + h ≤ 1800.
The organizers made an error in the first inequality. The given inequality 10s + 8h ≤ 1800 represents the total cost of buying shirts (10s) and hats (8h) should be less than or equal to $1800. However, this does not take into account the fact that the organizers want to buy at least 5 times as many shirts as hats, as indicated by the second inequality h ≥ 5s.
The correct way to represent this constraint is by using the equation s + h ≤ 1800, which ensures that the total number of shirts and hats purchased does not exceed $1800 in cost. This is because the organizers want to make sure that the total cost of shirts and hats combined does not exceed the budget of $1800.
the least number by which 7203 must be divided to make the result a perfect square is____
Answers
Answer:
Step-by-step explanation:
we should divide it by 3 to get a perfect square .and the square root of the perfect square is 49
\(\begin{gathered}\:\:\:\:\:\:\:\:\:\:\:\begin{gathered} \begin{array}{c|c} \underline{\sf{3}}& {\sf{ \underline{ \pink{7203} \: } \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: }} \\ \underline{\sf{7}}&{\sf{ \underline{2401 \: \: \: }\: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: }} \\\underline{\sf{7}}&{\sf{ \underline{343 \: \: \: \: \: }\: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: }} \\\underline{\sf{7}}&{\sf{ \underline{49\: \: \: \: \: }\: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: }} \\\underline{\sf{7}}&{\sf{ \underline{7 \: \: \: \: \: }\: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: }} \\\underline{\sf{}}&{\sf{ 1 \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: }} \end{array}\end{gathered}\end{gathered}\)
\(\qquad\)\(\purple{ \bf\longrightarrow 7203 = 3 \times 7 \times 7 \times 7 \times 7} \)
Clearly 3 has no pair! That means if we divide 7203 by 3, we get 2401 which is the square of 49. Hence, the smallest number by which 7203 must be divided to make the result a perfect square is 3.____________________________________________
(x-2)/(x+1) = ½. Find x
Answers
Answer:
x = 5
Step-by-step explanation:
\(\frac{x-2}{x+1}\) = \(\frac{1}{2}\) ( cross- multiply )
2(x - 2) = x + 1 ← distribute parenthesis on left side by 2
2x - 4 = x + 1 ( subtract x from both sides )
x - 4 = 1 ( add 4 to both sides )
x = 5
Find the slope or i'm maybe probably maybe most definitely gonna fail
I wasn't paying attention in class...

Answers
Therefore, the slope of the line passing through the points (0, 3) and (2, 6) is 3/2.
What is slope?In mathematics, the slope refers to the measure of steepness or inclination of a line. It is defined as the ratio of the vertical change (rise) between two points on the line to the horizontal change (run) between those points. In other words, the slope of a line is the change in y divided by the change in x between any two points on that line. The slope can be positive, negative, or zero, and it determines the direction and the steepness of the line. The slope is an important concept in algebra, geometry, and calculus, and it is used to describe many real-world phenomena, such as the velocity of an object, the rate of change of a function, and the growth or decline of a population.
Here,
To find the slope of the line passing through the points (0, 3) and (2, 6), we can use the formula:
slope = (change in y) / (change in x)
So, we have:
slope = (6 - 3) / (2 - 0)
slope = 3 / 2
To know more about slope,
https://brainly.com/question/29184253
#SPJ1
In the figure below, m1=2x° and m/2 = (x+87)°.
Find the angle measures.
1
2
m 21 =
m 22 = °

Answers
Answer:
∠ 1 = 62° , ∠ 2 = 118°
Step-by-step explanation:
the angles are a linear pair and sum to 180° , so
2x + x + 87 = 180
3x + 87 = 180 ( subtract 87 from both sides )
3x = 93 ( divide both sides by 3 )
x = 31
then
∠ 1 = 2x = 2 × 31 = 62°
∠ 2 = x + 87 = 31 + 87 = 118°
helppp<33 pls and ty..

Answers
Answer:
The answer is D
Step-by-step explanation:
Because we don't know whether the molecules are a solid, liquid or a gas
We don't know which element the molecules are part of
And we don't know which sugar it is/phosphate.
Hope that helps?
Which inference can be made when analyzing the data in the table?
Answers
Answer
Your saviour has come!
The answer is A
Step-by-step explanation:
Finding the nth derivative of y =
sinxcosx?
Answers
The nth derivative of y = sin(x)cos(x) is dⁿy/dxⁿ = (-1)^(n+1) * n! * sin(x)cos(x)
To find the nth derivative of y = sin(x)cos(x), we can use the product rule and the chain rule repeatedly. Let's go through the process step by step.
The given function is y = sin(x)cos(x).
First, let's find the first derivative (n = 1):
dy/dx = (cos(x)cos(x)) + (sin(x)(-sin(x)))
= cos^2(x) - sin^2(x)
Now, let's find the second derivative (n = 2):
d²y/dx² = d/dx[cos^2(x) - sin^2(x)]
= d/dx[cos^2(x)] - d/dx[sin^2(x)]
To find the derivative of cos^2(x), we can apply the chain rule:
d/dx[cos^2(x)] = 2cos(x)(-sin(x)) = -2sin(x)cos(x)
To find the derivative of sin^2(x), we can again apply the chain rule:
d/dx[sin^2(x)] = 2sin(x)cos(x)
Substituting these results back into the second derivative expression:
d²y/dx² = -2sin(x)cos(x) - 2sin(x)cos(x)
= -4sin(x)cos(x)
We can continue this process to find higher-order derivatives by differentiating the expression obtained for the (n-1)th derivative.
In summary, the nth derivative of y = sin(x)cos(x) is given by:
dⁿy/dxⁿ = (-1)^(n+1) * n! * sin(x)cos(x)
Note that the alternating signs (-1)^(n+1) arise due to the repeated application of the product rule.
Learn more about derivative at https://brainly.com/question/32525596
#SPJ11