Answers
Answer:
53°
Step-by-step explanation:
all triangles equal to 180°
the right hand angle is a 90° angle plus the 37° gives you 127 to find the answer you have to subtract 180 - 127 hence the answer 53°
37°+ 90° + x° = 180° (Traingle sum property)
127°+ x° = 180°
x° = 180° - 127°
x° = 53°
Hope it helps you.
Related Questions
Please help me if you can!
Find the value of x

Answers
9514 1404 393
Answer:
x = 7
Step-by-step explanation:
The angle bisector divides the sides proportionally.
(3x -12)/6 = 21/14
3x -12 = 9 . . . . . . . multiply by 6 and simplify
x -4 = 3 . . . . . . . . divide by 3
x = 7 . . . . . . . . . . . add 4
Good evening! Can someone please answer this, ill give you brainliest and your earning 50 points. Would be very appreciated.

Answers
Answer:
1. Set A
2. \(\textsf{Apply\:Difference\:of\:Two\:Squares\:Formula:\:}\left(a+b\right)\left(a-b\right)=a^2-b^2\)
3.
\((x+7)(x-7)\)
\(\implies a=x\:\textsf{and}\:b=7\)
\(\implies x^2-7^2=x^2-49\)
\((x-9)(x+9)=(x+9)(x-9)\)
\(\implies a=x\:\textsf{and}\:b=9\)
\(\implies x^2-9^2=x^2-81\)
\((4x-3)(4x+3)=(4x+3)(4x-3)\)
\(\implies a=4x\:\textsf{and}\:b=3\)
\(\implies (4x)^2-3^2=16x^2-9\)
4.
\((2x+5)(2x-5)\)
\(\implies a=2x\:\textsf{and}\:b=5\)
\(\implies (2x)^2-5^2=4x^2-25\)
5. \((x-6)(x-6)\)
Cannot use Difference of Two Squares Formula to expand this expression. To expand this expression, you would need to use the FOIL method: \(\left(a+b\right)\left(c+d\right)=ac+ad+bc+bd\)
\(\implies (x-6)(x-6)=x^2-6x-6x+(-6)^2=x^2-12x+36\)
Answer:
1.Set A
2.Aplyyanses of shortcut based
\( \beta \sin( \sec( \cos(e \alpha \% log_{14 |kkjja| }(?) ) ) ) bcaue \: f \: thd \: \: aakdx\)
Step-by-step explanation:
thire9
Simplify the expression by combining all the like terms 6+2x+5+4x
Answers
Answer:
6x+11
Step-by-step explanation:
6+2x+5+4x
4x+2x+6+5
(4x+2x)+(6+5)
6x+11
Answer:
6x +11
Step-by-step explanation:
group like terms (terms with the same variable and powers) together
(2x+4x) + (6+5)
6x +11
An employee earns a 25% commission rate on his sales. One day, he earned $175.
Answers
If he gets 25% of his sales, and he makes $175, that means $175 is it 25% of his sales.
There are 4 grams of sugar in 1/2 of a liter of a new sports drink. How much sugar is in 3⁄4 of a liter of the sports drink?
Answers
There are 6 grams of sugar in 3/4 of a liter of the sports drink. when There are 4 grams of sugar in 1/2 of a liter of a new sports drink.
To find out how much sugar is in 3/4 of a liter of the sports drink, we need to first calculate the total amount of sugar in 1 liter of the drink. Since there are 4 grams of sugar in 1/2 of a liter, then in 1 liter, there would be 4 x 2 = 8 grams of sugar.
Now that we know there are 8 grams of sugar in 1 liter, we can calculate how much sugar there is in 3/4 of a liter: 8 x (3/4) = 6 grams.
Therefore, there are 6 grams of sugar in 3/4 of a liter of the sports drink.
To learn more about grams:
https://brainly.com/question/11260752
#SPJ4
3. Which three lengths could be the lengths of the sides of a triangle?
A.) 10 cm, 14 cm, 23 cm
B.) 9 cm, 22 cm, 11 cm
C.) 7 cm, 25 cm, 11 cm
D.) 6 cm, 22 cm, 10 cm
Answers
Answer:
A.) 10 cm, 14 cm, 23 cm
Step-by-step explanation:
The sum of the two shortest lengths must exceed the longest length for the lengths to be able to form a triangle. This is only the case for ...
A.) 10 cm, 14 cm, 23 cm . . . . . 10+14=24>23
__
The other choices don't make it:
B.) 9+11=20<22
C.) 7+11=18<25
D.)6+10=16<22
Find The Derivative Of The Following Function. Y=(5t−1)(4t−4)^−1 Dt/dy=
Answers
Given function, `y = (5t - 1) / (4t - 4)^(-1)` To find `dt/dy`,We can start with the chain rule: (d/dt) [ (5t - 1) / (4t - 4)^(-1) ] = [(4t - 4)^(-1)] * (d/dt) [5t - 1] + (5t - 1) * (d/dt) [(4t - 4)^(-1)]`
Now we will find `(d/dt) [(4t - 4)^(-1)]`:Let `u = 4t - 4`Then `(4t - 4)^(-1) = u^(-1)`Applying the power rule, we get:`(d/dt) [(4t - 4)^(-1)] = (d/du) [u^(-1)] * (d/dt) [4t - 4]
= (-u^(-2)) * 4
= -4(4t - 4)^(-2)`
We can substitute the values of `(d/dt) [(4t - 4)^(-1)]` and `(d/dt) [5t - 1]` in the first equation derived from chain rule: On simplifying, we get: `dt/dy = (4t - 4)^2 [5/(4t - 4) + (-4)(5t - 1)/(4t - 4)^2]` Simplifying further, we get: `dt/dy = (4t - 4) [-5t + 9] / (4t - 4)^2 = (-5t + 9) / (4t - 4)` Therefore, the derivative of the function `y = (5t−1)(4t−4)^−1` with respect to `t` is
`dt/dy = (-5t + 9) / (4t - 4)`
To know more about function visit:
https://brainly.com/question/30721594
#SPJ11
D²y(t) + 12 Dy(t) + 36y(t) = 2 e-5t y(0) = 1, Dy(0)=0 Solve the differemtial equation using Classical Method (30pts) and Laplace Transform Method(30pts)
Answers
The solution to the differential equation D²y(t) + 12 Dy(t) + 36y(t) = 2 \(e^{(-5t)}\), with initial conditions y(0) = 1 and Dy(0) = 0, is \(y(t) = (1 + 6t) e^{(-6t)}\).
To solve the given differential equation using the classical method, we can assume a solution of the form \(y(t) = e^{(rt)}\) and find the values of r that satisfy the equation. We then use these values of r to construct the general solution.
Using the classical method:
Substitute the assumed solution \(y(t) = e^{(rt)}\) into the differential equation:
D²y(t) + 12 Dy(t) + 36y(t) = \(2 e^{(-5t)}\)
This gives the characteristic equation r² + 12r + 36 = 0.
Solve the characteristic equation for r by factoring or using the quadratic formula:
r² + 12r + 36 = (r + 6)(r + 6)
= 0
The repeated root is r = -6.
Since we have a repeated root, the general solution is y(t) = (c₁ + c₂t) \(e^{(-6t)}\)
Taking the first derivative, we get Dy(t) = c₂ \(e^{(-6t)}\)- 6(c₁ + c₂t) e^(-6t).\(e^{(-6t)}\)
Using the initial conditions y(0) = 1 and Dy(0) = 0, we can solve for c₁ and c₂:
y(0) = c₁ = 1
Dy(0) = c₂ - 6c₁ = 0
c₂ - 6(1) = 0
c₂ = 6
The particular solution is y(t) = (1 + 6t) e^(-6t).
Using the Laplace transform method:
Take the Laplace transform of both sides of the differential equation:
L{D²y(t)} + 12L{Dy(t)} + 36L{y(t)} = 2L{e^(-5t)}
s²Y(s) - sy(0) - Dy(0) + 12sY(s) - y(0) + 36Y(s) = 2/(s + 5)
Substitute the initial conditions y(0) = 1 and Dy(0) = 0:
s²Y(s) - s - 0 + 12sY(s) - 1 + 36Y(s) = 2/(s + 5)
Rearrange the equation and solve for Y(s):
(s² + 12s + 36)Y(s) = s + 1 + 2/(s + 5)
Y(s) = (s + 1 + 2/(s + 5))/(s² + 12s + 36)
Perform partial fraction decomposition on Y(s) and find the inverse Laplace transform to obtain y(t):
\(y(t) = L^{(-1)}{Y(s)}\)
Simplifying further, the solution is:
\(y(t) = (1 + 6t) e^{(-6t)\)
To know more about differential equation,
https://brainly.com/question/32622859
#SPJ11
two number cubes are rolled. Deterimine the number of ways that you could get a sum that is less than 5. The number cube is out of 6
Answers
Answer: six ways
Step-by-step explanation: The pairs when the cube is rolled that are less than five would be; (1,1), (1,2), (1,3), (2,1), (2,2), (3,1) since each cube is out of six.
On Monday, Jayla raised $30 and Carlos raised $50.
After that, Jayla raised $12 per day and Carlos
raised $7 per day. After how many days will they
have raised the same amount?
They will raise the same amount after days.
Answers
Answer:
84 days
Step-by-step explanation:
You would use the LCM to solve this.
12 and 7 don't share any common factors other than 1,
so you would multiply 12 x 7, which gets you 84.
After 84 days they would have raised the same amount.
i mark brianlest just help me;-;

Answers
Answer:
B)113.04 cm^2
Step-by-step explanation:
Answer:
B)113.04 cm^2
Step-by-step explanation:
circumference is 37.68
C=2πr
now the Area is
A=πr^2
we need to know the radius
so 37.68=2(3.14)r
divide both sides by 2(3.14)
get
r=6
now solve for area
A=(3.14)(6)^2
=113.04
Here is a grid of squares.write down the ratio of the number of unshaded to shaded squares
Answers
The ratio of the number of unshaded to shaded squares is 7 : 3.
What is Ratio?Ratio is defined as the relationship between two quantities where it tells how much one quantity is contained in the other.
It is also defined as the fraction of one quantity with respect to other.
The ratio of a and b is denoted as a : b.
Given is a grid of squares which is given below.
Total number of squares = 10
Of that,
Number of shaded squares = 3
Number of unshaded squares = 7
We have to find the ratio of unshaded to shaded squares in the grid which is 7 / 3 or 7 : 3.
Ratio of unshaded squares to shaded squares = 7 : 3
Hence 7 : 3 is the ratio of unshaded to shaded.
Solve more problems about Ratio here :
https://brainly.com/question/19761366
#SPJ9

Find the 82nd term of the following sequence.
-32, -27, -22, ....
Answers
Is this a proper fraction, improper fraction, mixed number?
4/8
Answers
Answer:
proper fraction
Step-by-step explanation:
if it was a mixed numebr an example: 1 4/8 If it was a imroper fraction an example: 12/8
Answer:
Proper fraction
Step-by-step explanation:
Proper fraction - A fraction with a numerator less than the denominator; proper fractions are fractions less than a whole. Ex. 5/8Mixed number - A number with an integer and a proper fraction. Ex. 2 1/2Improper fraction - A number with a numerator large than the denominator; a fraction larger than a whole. Ex. 8/5Q1.
Kristen buys a laptop.
She gets a discount of 20% off the normal price.
Kristen pays £480 for the laptop.
Work out the discount. Give your answer in pounds.
Answers
Answer:
320$
Step-by-step explanation:
monay cash burngert
real numbers $x$ and $y$ have an arithmetic mean of 7 and a geometric mean of $\sqrt{19}$. find $x^2+y^2$.
Answers
Real number \($x^2+y^2= \boxed{158}$\)
Let's start by using the formulas for arithmetic mean and geometric mean:
Arithmetic mean:
\($\frac{x+y}{2}=7 \Rightarrow x+y=14$\)
Geometric mean:
\($\sqrt{xy}=\sqrt{19} \Rightarrow xy=19$\)
Now, we can square the equation for the arithmetic mean:
\($(x+y)^2=14^2 \Rightarrow x^2+2xy+y^2=196$\)
Substituting\($xy=19$\), we get:
\($x^2+y^2+2(19)=196$\)
Simplifying:
\($x^2+y^2= \boxed{158}$\)
For similar questions on Real Number
https://brainly.com/question/17201233
#SPJ11
A certain train has 8 cars that are being lined up on a track. One of the cars is the engine, and another is the caboose. The engine will be the first car in line. The caboose will be the last car in line. In how many ways can the cars be lined up?
Answers
There are 20,160 ways the cars can be lined up on the track.
The total number of arrangements of n different things taken all at a time is given by n! (factorial), which means the product of all the numbers from 1 to n.
Here n=8.
To find the number of ways the cars can be lined up, we can use this formula:
8! = 8*7*6*5*4*3*2*1
8! = 40,320.
There are eight cars in total, but one of them has to be in the first position and another in the last position.
That leaves us with 6 cars to arrange in between the engine and caboose.
The number of ways to arrange those 6 cars is 6!, which is 720.
Therefore, the number of ways to line up the cars is:
8! / (2! x 6!) = 28 x 720 = 20,160.
Another way of doing this is by combination.
The formula for combination is:
nCr= n! / r! (n-r)!
Here n=8
r=2
n-r = 6
Therefore substituting,
nCr = 8! / (2! x 6!) = 28 x 720 = 20,160.
So there are 20,160 ways the cars can be lined up on the track.
learn more about combination here:
https://brainly.com/question/28720645
#SPJ11
help me pleaseeeeeeeeeeeeee!!!!

Answers
Answer:
The shorter leg measures 2.4 ft.
the longer leg measures 4.4 ft.
Step-by-step explanation:
Let the shorter leg have length a and the longer leg have length b.
The hypotenuse has length c.
a² + b² = c²
a² + (a + 2)² = 5²
a² + a² + 4a + 4 = 25
2a² + 4a - 21 = 0
This is not factorable, so we use the quadratic formula.
Switch the variable to x. Now x is the length of the shorter leg.
2x² + 4x - 21 = 0
\( x = \dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a} \)
\( x = \dfrac{-4 \pm \sqrt{4^2 - 4(2)(-21)}}{2(2)} \)
\( x = \dfrac{-4 \pm \sqrt{16 + 168}}{4} \)
\( x = \dfrac{-4 \pm \sqrt{184}}{4} \)
\( x = \dfrac{-4 \pm 2 \sqrt{46}}{4} \)
\( x = \dfrac{-2 \pm \sqrt{46}}{2} \)
We discard the negative solution since the length of a side of a triangle cannot be negative.
\( x = \dfrac{-2 + \sqrt{46}}{2} \)
\( x = 2.391 \)
\( x + 2 = 2.391 + 2 = 4.391 \)
The shorter leg measures 2.4 ft.
the longer leg measures 4.4 ft.
A frisbee is thrown into the air with an initial velocity of 40 feet per second. The release point is 5 feet above the ground. The function ℎ = −16푡 2 +40푡 + 5 represents the height h in feet of the frisbee after t seconds. (Answer both questions)(PHoto below)

Answers
a) The height of the frisbee each second it is in the air are 5, 29, 45, 53, 53, 45, 29, 5, -27 and -67.
b) The frisbee is in the air for a total of 8 seconds.
To find the height of the frisbee each second it is in the air, we need to substitute different values of t into the equation \(h = -16t^2 + 40t + 5\) and calculate the corresponding height.
a) Let's substitute t = 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9 into the equation:
When t = 0: \(h = -16(0)^2 + 40(0) + 5 = 5\)
When t = 1: \(h = -16(1)^2 + 40(1) + 5 = 29\)
When t = 2: \(h = -16(2)^2 + 40(2) + 5 = 45\)
When t = 3: \(h = -16(3)^2 + 40(3) + 5 = 53\)
When t = 4: \(h = -16(4)^2 + 40(4) + 5 = 53\)
When t = 5: h = \(-16(5)^2 + 40(5) + 5 = 45\)
When t = 6: h = \(-16(6)^2 + 40(6) + 5 = 29\)
When t = 7: h = \(-16(7)^2 + 40(7) + 5 = 5\)
When t = 8: h = \(-16(8)^2 + 40(8) + 5 = -27\)
When t = 9: h =\(-16(9)^2 + 40(9) + 5 = -67\)
b) The frisbee is in the air as long as its height is greater than 0. From the calculations above, we can see that the frisbee is in the air from t = 0 to t = 7, inclusive.
Note: The table you provided shows the height of the frisbee at each second it is in the air, but it seems to be cut off. However, based on the calculations above, the height values at each second should be as follows:
0 seconds: 5 feet
1 second: 29 feet
2 seconds: 45 feet
3 seconds: 53 feet
4 seconds: 53 feet
5 seconds: 45 feet
6 seconds: 29 feet
7 seconds: 5 feet
For more such questions on height
https://brainly.com/question/28990670
#SPJ8
Can you explain it if you could I don’t get it
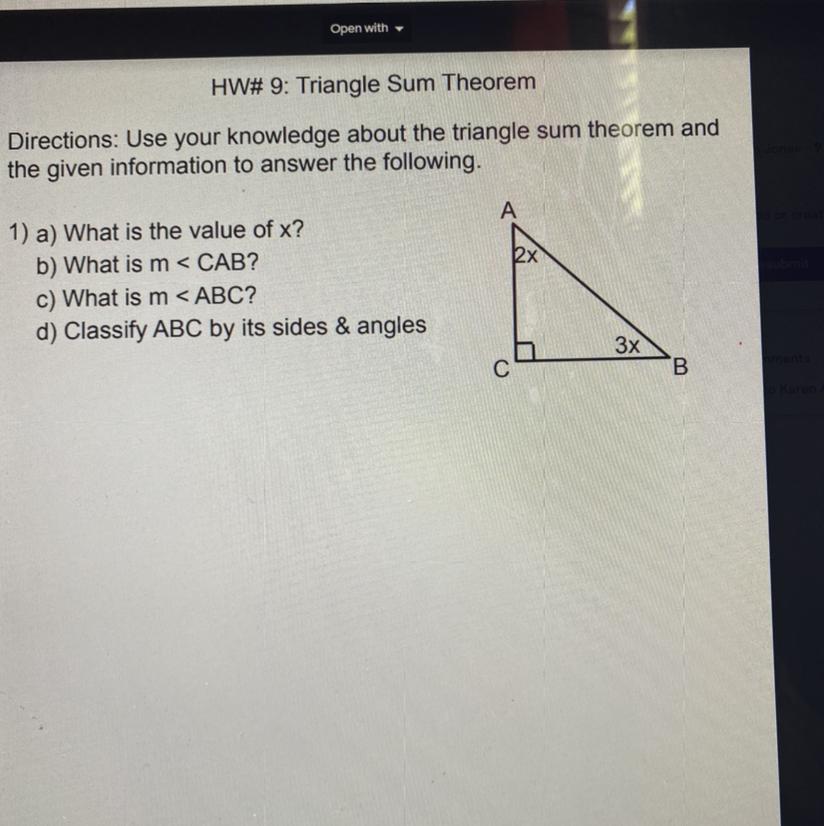
Answers
Step-by-step explanation:
The Triangle Sum Theorem states that the interior angles of a triangle add up to 180 degrees. A square for an angle symbolizes that the angle is 90 °, as is the case with angle ∠ACB.
Therefore, as ∠CAB = 2x and ∠ABC = 3x, and angles ∠ACB, ∠CAB, and ∠ABC make up the interior angles of the triangle, we can say that ∠ACB + ∠CAB + ∠ABC = 180, so 90 + 2x + 3x = 180
90 + 2x + 3x = 180
90 + 5x = 180
subtract 90 from both sides to separate the x and its coefficient
5x = 90
divide both sides by 5 to separate the x
x = 18
(a) ∠CAB = 2x = 18(2) = 36
(b) ∠ABC = 3x = 18(3) = 54
(c) Any triangle with a 90° angle is called a right triangle. This has a 90° triangle, and is therefore a right triangle. Similarly, a 90° angle in a triangle is called a right angle.
A cuboidal box with dimension 3×3×2 cu. Units is melted into another cuboid whose width is 15 units . Find the length and height of the cuboidformed if l=h
Answers
Answer:
Let's first find the volume of the original cuboidal box:
Volume = Length x Width x Height = 3 x 3 x 2 = 18 cubic units
We can then set up an equation to relate the volume of the original box to the volume of the new cuboid:
Volume of new cuboid = Volume of original box
Let's call the length and height of the new cuboid "x" (since we know that the length and height are the same). We know that the width of the new cuboid is 15 units. Therefore, we can write:
Volume of new cuboid = Length x Width x Height = x x 15 x x = 15x^2
Now we can set up the equation:
15x^2 = 18
Dividing both sides of the equation by 15 gives:
x^2 = 18/15
Simplifying the right side of the equation gives:
x^2 = 1.2
Taking the square root of both sides of the equation gives:
x ≈ 1.095
Therefore, the length and height of the new cuboid are approximately 1.095 units.
solve the problem in the image (fill in the blanks)

Answers
From the two column proof we have been able to show that:
m∠6 = 20° and m∠4 = 160°
How to solve the two column proof?Two column proof is one of the most common formal proofs in elementary geometry courses. The known or derived statements are written in the left column, and the reason why each statement is known or valid is written in the adjacent right column.
The complete two column proof is as follows:
Statement 1: a ║ b
Reason 1: Given
Statement 2: m∠6 = ¹/₈m∠4
Reason 2: Given
Statement 3: m∠6 + m∠4 = 180°
Reason 3: Supplementary Angles
Statement 4: m∠6 + 8*m∠4 = 180°
Reason 4: Substitution
Statement 5: m∠6 = 20° and m∠4 = 160°
Reason 5: Algebra
Read more about two column proof at: https://brainly.com/question/1788884
#SPJ1
The line in the xyxyx, y-plane above represents the relationship between the height h(x)h(x)h, (, x, ), in feet, and the base diameter xxx, in feet, for cylindrical Doric columns in ancient Greek architecture. How much greater is the height of a Doric column that has a base diameter of 555 feet than the height of a Doric column that has a base diameter of 222 feet
Answers
The height of a Doric column that has a base diameter of 555 feet is 666 feet greater than the height of a Doric column that has a base diameter of 222 feet.
Given that the line in the xyxyx, y-plane above represents the relationship between the height h(x)h(x)h, (, x, ), in feet, and the base diameter xxx, in feet, for cylindrical Doric columns in ancient Greek architecture.
The question is asking us to find the difference between the height of a Doric column that has a base diameter of 555 feet than the height of a Doric column that has a base diameter of 222 feet.
Let's solve the problem.
:Let the height of a Doric column with base diameter 222 feet be y1 and the height of a Doric column with base diameter 555 feet be y2.
Given equation of the line in the xy-plane as, y=2x+7
From the above equation, we have
y1=2(222)+7 y1=451 feet (approximately)
y2=2(555)+7 y2=1117 feet (approximately)
The height of the Doric column with a base diameter of 555 feet is 1117 feet and the height of the Doric column with a base diameter of 222 feet is 451 feet. So, the difference in their heights is 1117 - 451 = 666 feet.
Thus, the height of a Doric column that has a base diameter of 555 feet is 666 feet greater than the height of a Doric column that has a base diameter of 222 feet.
The height of a Doric column with a base diameter of 555 feet is 666 feet greater than the height of a Doric column with a base diameter of 222 feet. Using the equation of the line in the xy-plane y=2x+7, we have calculated the height of a Doric column with base diameter 222 feet as 451 feet (approximately) and the height of a Doric column with base diameter 555 feet as 1117 feet (approximately). So, the difference in their heights is 1117 - 451 = 666 feet.
Therefore, the height of a Doric column that has a base diameter of 555 feet is 666 feet greater than the height of a Doric column that has a base diameter of 222 feet.
To know more about diameter visit:
brainly.com/question/4771207
#SPJ11
given the points for segment AB where A (3,-4) and B (-9,0) find the point that is 1/4 the distance from A to B
Answers
To work this out I would use the midpoint formula. (x1+x2)/2 , (y1+y2)/2
Therefore, (3+-9)/2 , (-4+0)/2
= -6/2. , -4/2
= -3 , -2
Now we know the half way point from AB, now we will use the same formula but instead of point B we will substitue the midpoint to work out the 1/4 point
Therefore, (3+-3)/2, (-4+-2)/2
=. 0/2, -6/2
=. 0, -3
Therfore the 1/4 way point from AB is 0,-3
Show that the sum of the squares of 2 consecutive
odd numbers is 2 more than a multiple of 8.
Answers
The given statement about two consecutive odd numbers is true.
What is correlation?A statistical metric called correlation shows how closely two variables are connected or correlated with one another. It reveals if two variables are related, but it does not reveal whether one variable is the cause of the other. Contrarily, causation describes a link between two variables in which one variable has a direct impact on the other. A cause-and-effect link must be shown in order to prove causation, and this is frequently done through a well planned experiment that may focus on the impact of one variable on another.
Let us suppose the first odd number = x.
The second odd number will be = x + 2.
According to the given condition:
x² + (x+2)² = 8n + 2
2x² + 4x + 2 = 8n
x² + 2x + 1 = 4n
(x+1)² = 4n
Here, we have perfect squares on both sides.
As a result of this demonstrating that the left side is a multiple of four, the right side must likewise be a multiple of four. Hence, "n" has to be an even integer, such as "n = 2m."
Substituting this into the equation, we get:
(x+1)² = 8m
which shows that the left side is a multiple of 8, plus 2.
Hence, the given statement about two consecutive odd numbers is true.
Learn more about correlation here:
https://brainly.com/question/28898177
#SPJ1
Someone help me please

Answers
Answer:
\(27.13^o\)
Step-by-step explanation:
\(\mathrm{Here,}\\a=28\mathrm{yd}\\c=23\mathrm{yd}\\\\\mathrm{Using\ the\ sine\ law,}\\\mathrm{\frac{a}{sinA}=\frac{c}{sinC}}\\\\\mathrm{or, }\ \frac{28}{\mathrm{sin22^o}}=\frac{23}{\mathrm{sin}C}\\\\\mathrm{or,sinC}=\frac{23}{28}\mathrm{sin22^o}=0.307\\\\\mathrm{or,\ C=sin^{-1}0.307=17.92^o}\)
Which number line best represents the solution to the inequality 3.3w-9> -22.2?
Thanks in advance:)

Answers
The answer number line is G.
Given that the inequality 3.3w - 9 > -22.2, we need to find the value of w,
So,
3.3w - 9 > -22.2
Add 9 to both sides,
3.3w > -13.2
w > -4
Since the value of w is greater than -4 and the sign is > so the number line is G.
Hence the answer number line is G.
Learn more about inequality click;
https://brainly.com/question/30231190
#SPJ1
Insert 3 rational numbers between 1 /4 and 1/3 using mean method
Answers
Answer:
\( 1. \: \frac{7}{24} \)
\(2. \: \frac{13}{48} \)
\(3. \: \frac{5}{16} \)
Step-by-step explanation:
Hope it is helpful....

a plumber charges a rate of $65 per hour for his time but gives a discount of $7 per hour to senior citizens. write an expression which represents a senior citizen's total cost of plumber in 2 different ways
Answers
An equation highlighting the discount: y = (65 - 7)x
A simpler equation: y = 58x
when blotting dry a stained slide what will happen if you rub it from side to side
Answers
When blotting dry a stained slide, rubbing it from side to side may cause the stain to smear or even be removed from the slide completely. This can result in the loss of important information that was being observed under the microscope.
Stains are used to enhance the contrast of the sample being observed and make it easier to distinguish different structures or cells. The stain is absorbed by the sample and binds to specific parts of the cell or tissue, providing a clearer image. However, these stains are often water-soluble and can easily be removed by excessive rubbing or wiping.
To avoid damaging the stained slide, it is important to blot the slide gently and in one direction. The best technique is to use a soft, lint-free cloth or paper towel and gently press down on the slide to remove excess liquid. Blotting the slide in this way will help to prevent the stain from smearing and will preserve the quality of the image.
In conclusion, rubbing a stained slide from side to side while blotting dry can cause the stain to smear or be removed completely, resulting in the loss of important information. To avoid damaging the slide, it is important to blot gently and in one direction using a soft, lint-free cloth or paper towel.
To leran more about stain, refer:-
https://brainly.com/question/14949270
#SPJ11
