Answers
Answer:
given,
AB= 17
AC= 8
angle BCA =90°
as it is a Right angled triangle ,
taking reference angle BAC
we get,h=AB=17
b=AC=8
p=BC=?
now by the Pythagoras theorem we get,
p=
\( \sqrt{h { }^{2} - b {}^{2} } \)
so,p=
\( \sqrt{17 {}^{2} - 8 {}^{2} } \)
\( = \sqrt{225} \)
=15 is the answer....
hope its wht u r searching for....
Related Questions
what is the value of the expression 2c(c+3)^2 if c=2
Answers
After simplifying, what will x be equivalent to?
a2a4=ax
Answers
Answer:
x=8a
Step-by-step explanation:
Given data
We have the expression
a2a4=ax
Simplifying the LHS(Left Hand Side)
8a^2=ax
8a=x
Hence x will simplify to
x=8a
What number can be placed in the box to make this statement true?
If +7=10, then 10-7 = 0.
02
O 3
04
O 5
Answers
Answer: the number that can be placed in the box to make the statement true is 3.
Step-by-step explanation:
To make the statement true, we need to find a number that, when added to 7, equals 10. From the given options, the number that satisfies this condition is 3.
If we substitute 3 for the box in the statement, it becomes:
If +7=10, then 10-7=3.
Find the Length of ST

Answers
Step-by-step explanation:
Consider Similarity and enlargement
To get the enlargement factor,
Take the ratio result of any two similar sides. i.e
PQ/AB = 3.6/2 = 1.8
The enlargement factor is 1.8
To get ST, consider ED then multiply it by the enlargement factor. i.e
= 5 x 1.8
= 9
Ann and Ben translate documents from German into English.
A set of documents that would take Ann 10 days would take Ben 12 days.
Ann starts to translate the documents.
After 2 days Ann and Ben both work on translating the documents.
How many more days will it take to complete the work?
You must show your working.
Answers
Using the together rate, it will take more 3.45 days to complete the work.
Division is one of the four basic operations of arithmetic, the ways that numbers are combined to make new numbers. The other operations are addition, subtraction, and multiplication.
The together rate is given by the sum of each separate rate.
For this problem, the rates are given as follows,
Ann,1/10 = 0.1
Ben,1/12 = 0.0833
Together,1/x
Hence the amount completed in 2 days is:
2 x (0.1 + 0.0833) = 0.3666
The amount it would take them to complete 100% of the project working together is found by the together rate as follows,
x = 60/11
x = 5.45 days.
The time it would take to do the remaining 100 - 36.66 = 63.34% of the project is,
0.6334 x 5.45 = 3.45 days.
It will take more 3.45 days to complete the work.
to learn more about the together rate visit:
brainly.com/question/26555709
#SPJ9
suppose that the length of a certain rectangle is 7 meters less than four times its width. The perimeter of the rectangle is 46 meters. find the length and width of the rectangle.
Answers
The answer to the given question is length is 17m and width is 6m
Given that a rectangle's length is 7 meters less than its width.
And also given the perimeter of the rectangle is 46 meters.
We know that the rectangle's perimeter is twice the sum of its length and width.
l - length of the rectangle
w - width of the rectangle
P - perimeter of the rectangle
Then we have P = 2 × (l + w)
Given that a rectangle's length is 7 meters less than its width.
⇒ l = 4 × w - 7
Given the perimeter of the rectangle is 46 centimeters.
⇒ 2 × ( l + w) = 46
⇒ 2 × (4w - 7 + w) = 46 (using the value of length given in terms of width)
⇒ 4w - 7 + w = 23 (dividing by 2 on both the sides)
⇒ 5w - 7 = 23
⇒ 5w = 23 + 7
⇒ 5w = 30
⇒ w = 6 (dividing both sides by 5)
Using the width value in the length equation, we get
l = 4 × 6 - 7
⇒ l = 24 - 7
⇒ l = 17
Therefore, The rectangle is 17 meters in length and 6 meters in width.
Learn more about Perimeters here:
https://brainly.com/question/24571594
#SPJ9
Please help will mark Brainly

Answers
The number of tickets day and evening combined should be more then 8 since it says at least 8 tickets. However the cost of the tickets which is 15x+30y (multiply the amount of tickets bought by the cost) should be less then 300 bucks since they have a budget. Hope this helps!
The graph of the step function g(x) = -[x] + 3 is shown.y05-5-4-3-2-140342+1+I-2+-3+-4+-5-& w1 2 35 xWhat is the domain of g(x)?O x x is a real number}Ox x is an integer}O {x1-2 ≤x<5}O {x-1 ≤ x ≤ 5}
![The graph of the step function g(x) = -[x] + 3 is shown.y05-5-4-3-2-140342+1+I-2+-3+-4+-5-& w1 2](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/xZgx1zVMc4vTvd4buiqrH4oV5RBlsZLS.jpeg)
Answers
The domain of a function is the set of all values that the independent variable can take. In this case, there are no restrictions over the values that x can take for the expression to be well defined (two common restrictions are non-negative square roots and nonzero denominators).
Therefore, the domain of g(x) is the set of all real numbers.
The correct choice is the first option: {x | x is a real number}
SHARE 300 USING 2:3:5
Answers
If we divide 300 into parts using the ratio 2:3:5, we get:
2 parts = 2/10 of the total ratio = 2/10 x 300 = 60
3 parts = 3/10 of the total ratio = 3/10 x 300 = 90
5 parts = 5/10 of the total ratio = 5/10 x 300 = 150
Therefore, 300 divided in the ratio 2:3:5 would result in three parts of 60, 90, and 150.
I hope I helped!
~~~Harsha~~~
-1000 2/3 is not real fraction. True or false
Answers
True, While "-1000 2/3" is not a real fraction, it can be represented as the improper fraction -2998/3.
The statement "-1000 2/3 is not a real fraction" is true. A real fraction is a mathematical expression that represents a ratio of two real numbers. In a fraction, the numerator and denominator are both real numbers, and they can be positive, negative, or zero.
In the given statement, "-1000 2/3" is not a valid representation of a fraction. The presence of a space between "-1000" and "2/3" suggests that they are separate entities rather than being part of a single fraction.
To represent a mixed number (a whole number combined with a fraction), a space or a plus sign is typically used between the whole number and the fraction. For example, a valid representation of a mixed number would be "-1000 2/3" or "-1000 + 2/3". However, without the proper formatting, "-1000 2/3" is not considered a real fraction.
It's important to note that "-1000 2/3" can still be expressed as an improper fraction. To convert it into an improper fraction, we multiply the whole number (-1000) by the denominator of the fraction (3) and add the numerator (2). The result would be (-1000 * 3 + 2) / 3 = (-3000 + 2) / 3 = -2998/3.
In conclusion, while "-1000 2/3" is not a real fraction, it can be represented as the improper fraction -2998/3.
for more such question on fraction visit
https://brainly.com/question/30122573
#SPJ8
SOMEONE ANYONE PLEASE HELP!!!

Answers
The graph of g(x) is obtained from the graph of f(x) by the following transformations:
- A horizontal stretch by a factor of 9. This is because the graph of g(x) is 9 times wider than the graph of f(x).
- A vertical translation down by 2 units. This is because the graph of g(x) is 2 units lower than the graph of f(x).
In other words, to obtain the graph of g(x) from the graph of f(x), we stretch the graph horizontally by a factor of 9 and then translate it down by 2 units.
Here is a more detailed explanation of the transformations:
- Horizontal stretch by a factor of 9: To stretch the graph horizontally by a factor of 9, we multiply all of the x-coordinates by 9. This means that every point on the graph of f(x) will be moved 9 units to the right on the graph of g(x).
- Vertical translation down by 2 units: To translate the graph down by 2 units, we subtract 2 from all of the y-coordinates. This means that every point on the graph of f(x) will be moved 2 units down on the graph of g(x).
which of these terms does not describe polygon A’B’C’D?
a. transformation
b. rotation
c. image
d. reflection
Answers
The terms that does not describe polygon A’B’C’D should be considered as the option D. reflection.
What is reflection?In terms of geometry, a reflection should be known as the flip, It should be considered as the mirror image of the shape. The image should reflect via the line that we called as the reflection line.
When it should be at reflection so each and every point in the figure should be equidistant with respect to the another figure.
hence, The terms that does not describe polygon A’B’C’D should be considered as the option D. reflection.
Learn more about polygon here: https://brainly.com/question/24452286
A study found that a 95% confidence interval for the mean μ of a particular population was computed from a random sample of 1200 people and found it to be 10 ± 4. Therefore, we may conclude:_______
Answers
Answer:
95% confidence interval for the mean μ is (6,14)
The Population mean μ lies between ( 6, 14 )
Step-by-step explanation:
Explanation:-
Given random sample 'n' = 1200
95% confidence interval for the mean μ is determined by
\((x^{-} -Z_{\alpha } \frac{S.D}{\sqrt{n} } , x^{-} +Z_{\alpha } \frac{S.D}{\sqrt{n} } )\)
Level of significance = 95% 0r 0.05
Z₀.₀₅ = 1.96
\((x^{-} -Z_{\alpha } \frac{S.D}{\sqrt{n} } , x^{-} +Z_{\alpha } \frac{S.D}{\sqrt{n} } )\) = 10 ± 4
Mean of the small sample = 10
95% of confidence intervals are
( 10 ±4 )
( 10 -4 , 10+4)
( 6 , 14 )
95% confidence interval for the mean μ lies between ( 6, 14 )
Elena is organizing her craft supplies. She estimatesthat her jars will fit 1,000 buttons or 50 large beads.They actually fit 677 buttons or 22 large beads. DoesElena's estimate about the buttons or her estimateabout the large beads have less percent error? To thenearest percent, how much less?
Answers
Step 1
Given;
\(\begin{gathered} Elena-\text{ estimates her jar will take 1000 buttons or 50 large beads} \\ Her\text{ Jar actually takes 677 buttons or 22 large beads} \end{gathered}\)Required; To find if Elena's estimates have percentage error, to which percent, and how much less
Step 2
State the formula for percentage error
\(\text{ \% error=}\frac{|Approximate-exact|}{exact}\times100\)\(Elena^{\prime}s\text{ estimate about the button has a percentage error }\)\(\begin{gathered} For\text{ buttons} \\ Approximate=1000 \\ Exact=677 \end{gathered}\)\(\text{ \%error=}\frac{|1000-677|}{677}\times100=47.71048744\text{\%}\)\(\begin{gathered} For\text{ large beads} \\ \operatorname{\%}\text{error=}\frac{\text{\lvert50-22\rvert}}{22}\times100 \end{gathered}\)\(\text{ \% error=}\frac{28}{22}\times100=127.272727...\text{\%}\)Percent errors tells you how big your errors are when you measure something in an experiment. Smaller values mean that you are close to the accepted or real value. For example, a 1% error means that you got very close to the accepted value, while 45% means that you were quite a long way off from the true value.
The percentage error for buttons with about 47.71% is less than that of the large beads which is about 127.273%.
How much less of the percentage error to the nearest percent will be;
\(\begin{gathered} =79.56223986 \\ \approx80\text{\%} \end{gathered}\)Simplify by expressing fractional exponents instead of radicals.

Answers
9. In the figure shown ABCD is a rectangle, DE ~ FC, BC EC, and F is the midpoint
of BC. Find the perimeter of AAEF. Give an exact answer.
A
D
2
E
B
F
C

Answers
The perimeter of the right triangle is 15 units
How to find the perimeter of the triangleThe dimensions of the triangle is solved by Pythagoras theorem given by the the formula
hypotenuse² = opposite² + adjacent²
Since F is mid segment then BF = F'C and DE = 2 = F'C
hence B'C = B'F + F'C = 2 + 2 = 4
In a rectangle B'C = AD = 4 = EC
F'E² = F'C² + EC²
F'E² = 2² + 4²
F'E² = 4 + 16
F'E = √20
F'E = 4.47
Solving for AE
AE² = AD² + DE²
AE² = 2² + 4²
AE² = 4 + 16
AE = √20
AE = 4.47
Solving for A'F
A'F² = AE² + FE²
A'F² = √20² + √20²
A'F² = 20 + 20
A'F = √40
A'F = 6.32
The perimeter of the triangle is
P = A'F + AE + FE
P = 6.32 + 4.47 + 4.47
P = 15.26
Learn more on Pythagoras theorem here:
https://brainly.com/question/29363020
#SPJ1
A store is having a sale on jelly beans and almonds. For 3 pounds of jelly beans and 5 pounds of almonds, the total cost is $27. For 9 pounds of jelly beans and
7 pounds of almonds, the total cost is $51. Find the cost for each pound of jelly beans and each pound of almonds.
Cost for each pound of jelly beans:
Cost for each pound of almonds:
Answers
Answer:
Cost for each pound of jelly beans: $2.75
Cost for each pound of almonds: $3.75
Step-by-step explanation:
Let J be the cost of one pound of jelly beans.
Let A be the cost of one pound of almonds.
Using the given information, we can create a system of equations.
Given 3 pounds of jelly beans and 5 pounds of almonds cost $27:
\(\implies 3J + 5A = 27\)
Given 9 pounds of jelly beans and 7 pounds of almonds cost $51:
\(\implies 9J + 7A = 51\)
Therefore, the system of equations is:
\(\begin{cases}3J+5A=27\\9J+7A=51\end{cases}\)
To solve the system of equations, multiply the first equation by 3 to create a third equation:
\(3J \cdot 3+5A \cdot 3=27 \cdot 3\)
\(9J+15A=81\)
Subtract the second equation from the third equation to eliminate the J term.
\(\begin{array}{crcrcl}&9J & + & 15A & = & 81\\\vphantom{\dfrac12}- & (9J & + & 7A & = & 51)\\\cline{2-6}\vphantom{\dfrac12} &&&8A&=&30\end{array}\)
Solve the equation for A by dividing both sides by 8:
\(\dfrac{8A}{8}=\dfrac{30}{8}\)
\(A=3.75\)
Therefore, the cost of one pound of almonds is $3.75.
Now that we know the cost of one pound of almonds, we can substitute this value into one of the original equations to solve for J.
Using the first equation:
\(3J+5(3.75)=27\)
\(3J+18.75=27\)
\(3J+18.75-18/75=27-18.75\)
\(3J=8.25\)
\(\dfrac{3J}{3}=\dfrac{8.25}{3}\)
\(J=2.75\)
Therefore, the cost of one pound of jelly beans is $2.75.
What is the correct answer?

Answers
Answer:
C
Step-by-step explanation:
Answer:
I think your answer is C
Step-by-step explanation:
The action of rotating around an axis or center.
Hope this helps
i got yelled at for my grandma giving a coney dog at A and W and she got sick is there a way i can cut my dad out of his life
Answers
Answer:
this whole sentence confused me a lot
Step-by-step explanation:
yes there is, but it depends on how you want to do it
Answer:
I don't really get what you're implying can you please explain?
Step-by-step explanation:
haha this just really confused me :)
-8=n-9 whats the answer?
Answers
Answer:
Step-by-step explanation:
n - 9 = -8
n = 1
\(\text {Hello! To find n you must...}\)
\(\text {Flip the Equation:}\)
\(\text {Before: -8=n-9}\\\text {After: n-9=-8}\)
\(\text {Note: You need to flip the equation to solve n and what it equals to.}\)
\(\text {The Final Step is to add 9:}\)
\(\text {n-9+9=-8+9}\)
\(\text {Your answer will be}\)
\(\fbox {n=1}\)
\(\text {Note: Instead of subtracting 9 we add 9 so they can cancel out.}\) \(\text { We are finding n so we need it to cancel out.}\)
\(\text {Best of Luck!}\)
\(\text {-LimitedX}\)
please help on geometry :((((
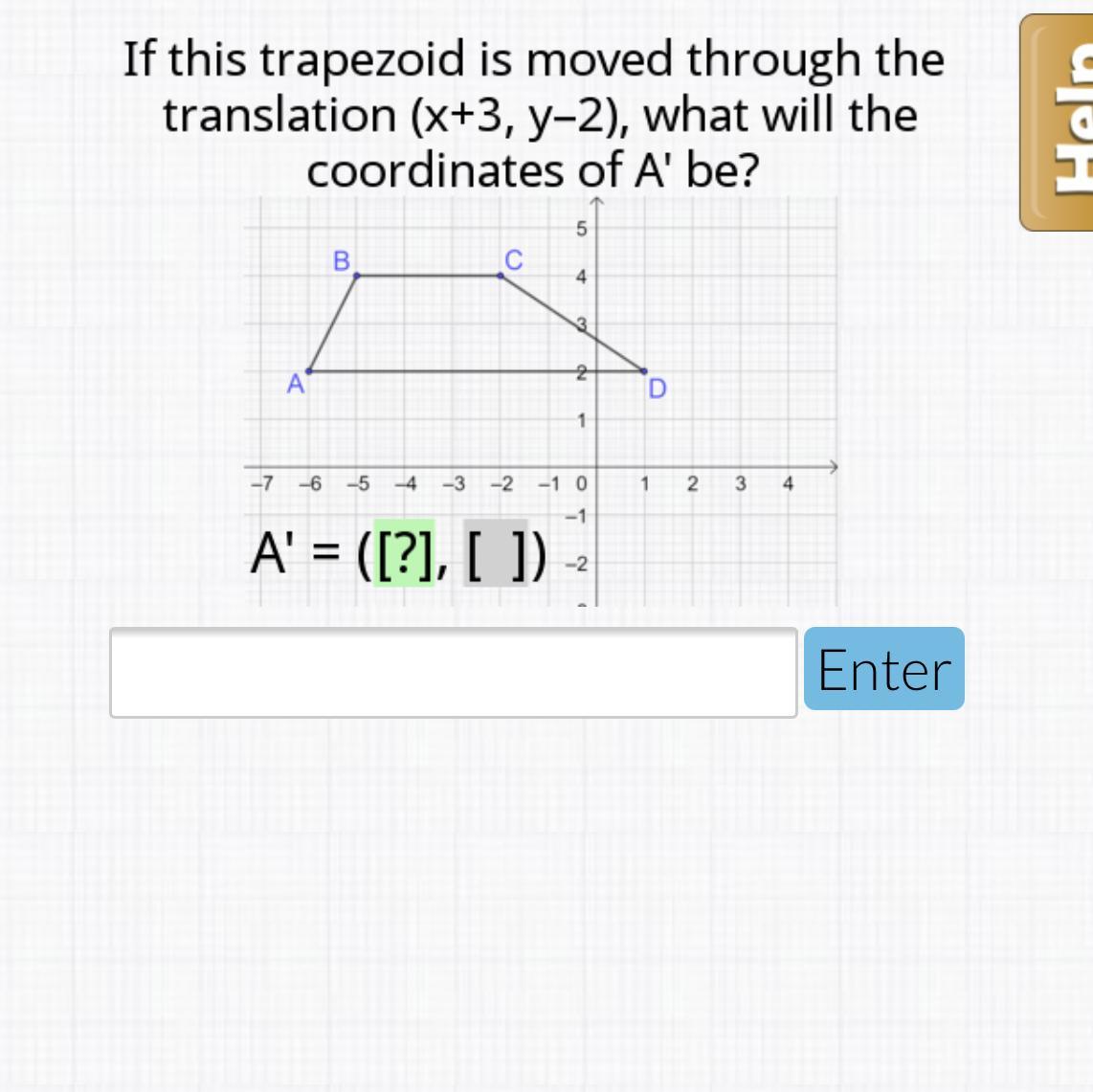
Answers
Answer:
(-3, 0)
Step-by-step explanation:
Answer:
(-3,0)
Step-by-step explanation:
you just have to take the coordinates of a and add 3 to the x value (-6+3=-3) and subtract 2 from the y value (2-2=0) so the coordinates of a on the new image would be (-3,0)
Hope this helps (:
Solve for x:
-5 - 3(6x-8) = -5x + 19
Show your work
Answers
Answer: x = 0
Step-by-step explanation:
simplify the expression
−5−3(6x−8)=−5x+19
−5−18+24=−5+19
19−18x=−5x+19
−18+19=−5+19
−5−3(6x−8)=−5x+19
−18x+19=−5x+19
−5−3(6x−8)=−5x+19
−18x+19=−5x+19
−18+19−19=−5+19−19
−18x=−5x+19 − 19
−18x+19−19=−5x+19 − 19
−18x=−5x
−18x+5x=−5x+5x
x=−5x+5x−13
x−13=−5+5
−13x=0
−13x/−13 = 0/-13
x= 0/−13
x= 0
-18x-5+24=-5x+19
-18x+19=-5x+19
19-19=-5x+18x
0=13x
Therefore x=0 (since 13 multiplied by 0 is 0)
Molly's scout troop sold 148 boxes of cookies last month and 165 boxes this month. Find the percent of increase, rounded to the nearest tenth of a percent.
Answers
The percent of the increase, rounded to the nearest tenth of a percent, concerning the sales of boxes of cookies that Molly sold last month and this month, is 11.5%.
How is the percentage increase determined?The percentage increase can be determined by finding the difference or the amount of increase in sales.
This difference is divided by the previous month's sales and multiplied by 100.
The total number of boxes of cookies Molly's Scout Troop sold last month = 148
The total number sold this month = 165
The increase = 17 (165 - 148)
Percentage increase = 11.5% (17 ÷ 148 x 100)
Learn more about percentage increases at https://brainly.com/question/28398580.
#SPJ1
Please help for a TEST tomorrow!!

Answers
Answer:
sorry for my bad writing

Solve each system using the substitution method.
y= 2x
5x - y =9
Answers
Answer:
{y,x}={6,3}
Explanation
System of Linear Equations entered :
[1] y=2x
[2] 5x-y=9
Equations Simplified or Rearranged :
[1] y - 2x = 0
[2] -y + 5x = 9
Graphic Representation of the Equations :
-2x + y = 0 5x - y = 9
Solve by Substitution :
// Solve equation [1] for the variable y
[1] y = 2x
// Plug this in for variable y in equation [2]
[2] -(2x) + 5x = 9
[2] 3x = 9
// Solve equation [2] for the variable x
[2] 3x = 9
[2] x = 3
// By now we know this much :
y = 2x
x = 3
// Use the x value to solve for y
y = 2(3) = 6
Solution :
{y,x} = {6,3}
A function is created to model the situation where the day of the month, x, is the independent variable, and the height of low tide, T, is the dependent variable. Plot the two points that we know on a graph. Include a dotted line representing the monthly average low tide height, and appropriately label the axes. Note that x = 1 is July 1.
i also have to show on the graph and the height only goes up to 2 then x axis is dates in july
Answers
In this graph, we have plotted the two known points as dots, and the monthly average low tide height as a dotted line.
What is function?In mathematics, a function is a relation between a set of inputs (called the domain) and a set of possible outputs (called the range), with the property that each input is associated with exactly one output. In other words, a function is a rule that assigns to each input a unique output. Functions are used in many areas of mathematics, science, engineering, and everyday life to model relationships between quantities, make predictions, analyze data, and solve problems. They are a fundamental concept in calculus, which deals with the rates of change of functions, and in many other branches of mathematics.
Here,
However, some general considerations can be made:
Both sine and cosine functions oscillate between -1 and 1, so they are often used to model periodic phenomena, such as tides.
The choice between sine and cosine depends on the phase of the oscillation, i.e., the starting point of the cycle. For example, a sine curve starts at zero and reaches its maximum at pi/2, while a cosine curve starts at its maximum and reaches zero at pi/2. If the data points given correspond to a minimum value of the tide, then a sine curve might be more appropriate, since it starts at zero and reaches its minimum at pi/2. On the other hand, if the data points correspond to a maximum value of the tide, then a cosine curve might be more appropriate, since it starts at its maximum and reaches zero at pi/2.
The choice between sine and cosine can also depend on the origin of the x-axis. In this case, x = 1 corresponds to July 1, so the origin is shifted by pi/2 from the usual position. This means that a sine curve that starts at zero at x = 1 would be shifted to the right by pi/2 compared to a cosine curve that starts at its maximum at x = 1.
Based on these considerations, we cannot definitively say whether a sine or cosine curve would be a better model without more information about the data. However, we can plot the two known points and the monthly average low tide height on a graph and see which curve seems to fit better visually. We can then use this visual inspection to guide our choice of model.
To know more about function,
brainly.com/question/28193995
#SPJ1
I need to know how to do this problem please

Answers
Answer: Total expenses if 3 widgets are produced is $11,018.00
Step-by-step explanation: The variable cost per unit is given by the coefficient of q in the expense function. In this case, the variable cost is $6.00 per widget. To find the variable costs to produce 2 widgets, we simply multiply the variable cost per unit by the number of units produced: Variable costs for 2 widgets = 2 x $6.00 = $12.00 Therefore, the variable costs to produce 2 widgets is $12.00. To find the variable costs to produce q widgets, we simply multiply the variable cost per unit by the number of units produced: Variable costs for q widgets = q x $6.00 = $6q Therefore, the variable costs to produce q widgets is $6q. To find the total expenses if 3 widgets are produced, we can use the expense function and substitute q = 3:E = 6.00 q + 11,000
E = 6.00 (3) + 11,000
E = 18.00 + 11,000
E = 11,018.00 Therefore, the total expenses if 3 widgets are produced is $11,018.00.
A manufacturer has 576 square inches of material available to construct the 6 faces of a carton, which will be in the shape of a rectangular prism. To maximize the volume, the carton will have dimensions such that the length and width are each twice the height.
Answers
To maximize the volume, of the rectangular prism, the carton should have dimensions of approximately 10.74 inches (length), 10.74 inches (width), and 5.37 inches (height).
What is the dimension required to maximize the volume of the box?Assuming the height of the rectangular prism is h inches.
According to the given information, the length and width of the prism will be twice the height, which means the length is 2h inches and the width is also 2h inches.
The total surface area of the rectangular prism is given by the formula:
Surface Area = 2lw + 2lh + 2wh
Substituting the values, we have:
576 = 2(2h)(2h) + 2(2h)(h) + 2(2h)(h)
576 = 8h² + 4h² + 4h²
576 = 16h² + 4h²
576 = 20²
h² = 576/20
h² = 28.8
h = √28.8
h = 5.37
The height of the prism is approximately 5.37 inches.
The length and width will be twice the height, so the length is approximately 2 * 5.37 = 10.74 inches, and the width is also approximately 2 * 5.37 = 10.74 inches.
Learn more on maximizing volume here;
https://brainly.com/question/10373132
#SPJ4
Which of the following equations are equivalent? Select three options. 2 + x = 5 x + 1 = 4 9 + x = 6 x + (negative 4) = 7 Negative 5 + x = negative 2
Answers
The three equivalent equations are 2 + x = 5, x + 1 = 4 and -5 + x = -2. So, correct options are A, B and E.
Two equations are considered equivalent if they have the same solution set. In other words, if we solve both equations, we should get the same value for the variable.
To determine which of the given equations are equivalent, we need to solve them for x and see if they have the same solution.
Let's start with the first equation:
2 + x = 5
Subtract 2 from both sides:
x = 3
Now let's move on to the second equation:
x + 1 = 4
Subtract 1 from both sides:
x = 3
Notice that we got the same value of x for both equations, so they are equivalent.
Next, let's look at the third equation:
9 + x = 6
Subtract 9 from both sides:
x = -3
Since this value of x is different from the previous two equations, we can conclude that it is not equivalent to them.
Now, let's move on to the fourth equation:
x + (-4) = 7
Add 4 to both sides:
x = 11
This value of x is also different from the first two equations, so it is not equivalent to them.
Finally, let's look at the fifth equation:
-5 + x = -2
Add 5 to both sides:
x = 3
Notice that we got the same value of x as the first two equations, so this equation is also equivalent to them.
So, correct options are A, B and E.
To learn more about equations click on,
https://brainly.com/question/29266004
#SPJ1
Complete question is:
Which of the following equations are equivalent? Select three options.
2 + x = 5
x + 1 = 4
9 + x = 6
x + (- 4) = 7
- 5 + x = - 2
please help! Evaluate the following function.
f(x) = -x – 8 for f(-1)

Answers
Answer:
x - 8
Step-by-step explanation:
Plug in -1 for x and you get x - 8
