Answers
A rectangle is a quadrilateral having opposite sides equal
The perimeter is given by the formula
\(2(L+B)\)The area is given by
\(L\times B\)To get the maximum area
If the fence is rectangular, it will have the largest possible area when the length equals the width. In order to have a perimeter of 480 feet, that means that each side needs to be 120 feet.
For any given rectangle, the area is maximized when all the sides are equal
Thus, the maximum area is
\(120ft\text{ by 120ft}\)Thus, the length is
\(\begin{gathered} \text{Length}=120ft \\ \text{Width}=120ft \end{gathered}\)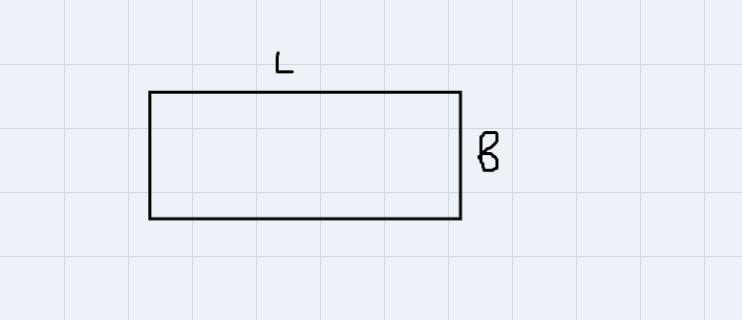
Related Questions
What is the slope of the line that passes through the points
( 9, 4) and (9, -5)
Answers
Answer:
x = 9
Step-by-step explanation:
Answer:
\(slope \: = \frac{ y_{2} - y_{1} }{ x_{2} - x_{1} } \)
\( = \frac{ - 5 - 4}{9 - 9} \)
\( = \infty \)
Let f(x)=5x+2 and gx=x^2-4x+1
\(\frac{f}{g}(5)\)
Answers
Answer:
find f(5) and g(5) then divide f(5) by g(5) i.e f(5)/g(5) Answer will be 25/6
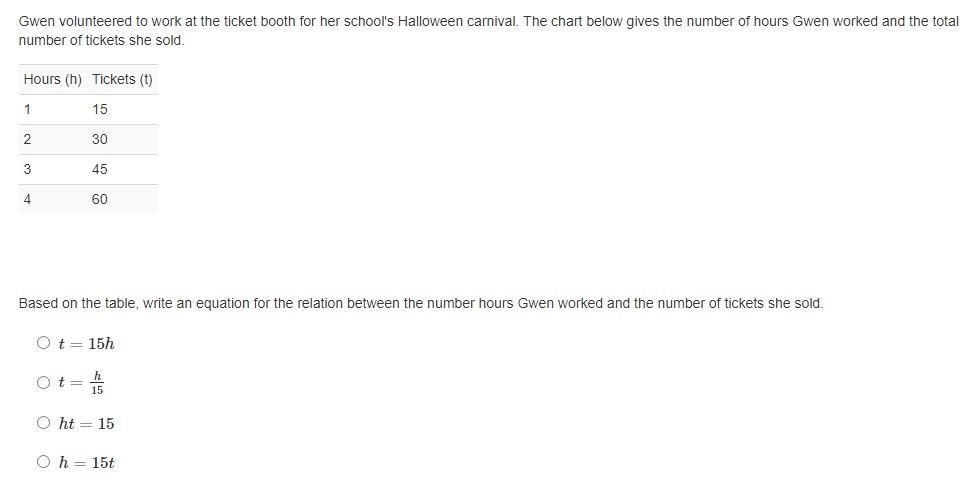
HELP! HELP! HELP! HELP!: Gwen volunteered.....
Answers
Answer:
Based on the table, the relationship between the number of hours Gwen worked and the number of tickets she sold is
t=15h
Question 6
If a truck can drive 24,4 miles in 1 gallon, how many miles would I be able to drive with a filled 30 gallon tank?
Answers
Answer: 732 mi
Step-by-step explanation:
Assuming you meant 24.4
Find the indefinite integral of each of the following by using [ f'(x)[f(x)"]dx =[ [f(x)]^n+1 / n+1] + c, where n #1
(a) e^x (3 - e^x)^4 dx
(b) 3e^2x √(1 + e²x) dx
(c) 3e^-2x / (1 + e^-2x)^3 dx
(d) 4 cos 2x sin³ 2x dx
(e) sec² 3x tan³ 3x dx
(f) 2+tan ² x / cos² x dx
![Find the indefinite integral of each of the following by using [ f'(x)[f(x)"]dx =[ [f(x)]^n+1 / n+1]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/MCSoClwul951aXbKM4ngkyTPM2bmCYjW.jpeg)
Answers
Answer:
a) e^x (3 - e^x)^4 dx
Using the formula [ f'(x)[f(x)"]dx =[ [f(x)]^n+1 / n+1] + c, where n = 1,
we have:
e^x (3 - e^x)^4 dx = (e^x)^5 (3 - e^x)^4 / 5 + c
= (e^5x - 4e^4x + 6e^3x - 4e^2x + e^x) / 5 + c
b) 3e^2x √(1 + e²x) dx
Using the formula [ f'(x)[f(x)"]dx =[ [f(x)]^n+1 / n+1] + c, where n = 1,
we have:
3e^2x √(1 + e²x) dx = (3e^2x)^2 * (1 + e²x)^(3/2) / 2 + c
= (9e^4x + 3e^2x) / 2 + c
c) 3e^-2x / (1 + e^-2x)^3 dx
Using the formula [ f'(x)[f(x)"]dx =[ [f(x)]^n+1 / n+1] + c, where n = 1,
we have:
3e^-2x / (1 + e^-2x)^3 dx = -(3e^-2x)^2 / (1 + e^-2x)^2 + c
= -(9e^-4x) / (e^-4x + 2e^-2x + 1) + c
d) 4 cos 2x sin³ 2x dx
Using the formula [ f'(x)[f(x)"]dx =[ [f(x)]^n+1 / n+1] + c, where n = 1,
we have:
4 cos 2x sin³ 2x dx = -4 cos 2x (sin 2x)^4 / 4 + c
= -(cos 2x) (1 - cos 4x)^2 / 2 + c
e) sec² 3x tan³ 3x dx
Using the formula [ f'(x)[f(x)"]dx =[ [f(x)]^n+1 / n+1] + c, where n = 1,
we have:
sec² 3x tan³ 3x dx = -sec² 3x (tan 3x)^4 / 4 + c
= -sec² 3x (sec² 3x - 1)^2 / 4 + c
f) 2+tan ² x / cos² x dx
Using the formula [ f'(x)[f(x)"]dx =[ [f(x)]^n+1 / n+1] + c, where n = 1,
we have:
2+tan ² x / cos² x dx = ln|sec x| + c
It's worth noting that all these integrals are indefinite, which means that the constant c is arbitrary, and the actual antiderivative depends on the problem context.
Step-by-step explanation:
Based on the scatterplot below what is most likely the value for “pounds of apples” when “Numbers of Apples” is 60

Answers
Answer:
36
Step-by-step explanation:
Place value of 4 in 265 473
Answers
Answer:
The place value of 4 in 265 473 is 40,000
Answer:
Step-by-step explanation:
Order:
3 is in the ones place and has a value of 3
7 is in the tens place and has a value of 70
4 is in the hundreds place and has a value of 400
5 is in the thousands place and has a value of 5000
6 is in the ten thousands place and has a value of 60,000
2 is in the hundred thousands place and has a value of 200,000
Suppose That \( R \) Is The Finite Region Bounded By \( Y=X, Y=X+1, X=0 \), And \( X=3 \). find the exact value of the volume of the object we obtain when rotating about the -axis.
Answers
Step-by-step explanation:
Find Object Volume Rotation
Suppose That \( R \) Is The Finite Region Bounded By \( Y=X, Y=X+1, X=0 \), And \( X=3 \). find the exact value of the volume of the object we obtain when rotating about the -axis.
The region R is a triangular region defined by the lines y = x, y = x + 1, x = 0, and x = 3. To find the volume of the object obtained by rotating this region about the x-axis, we can use the method of cylindrical shells.
The height of the cylindrical shell is given by the difference between y = x and y = x + 1, or 1 unit. The radius of the cylindrical shell is given by x. Therefore, the volume of the object is given by:
\begin{align*}
V &= \int_{x=0}^{x=3} \pi x^2 \cdot 1, dx \
&= \pi \int_{x=0}^{x=3} x^2, dx \
&= \pi \left[ \frac{x^3}{3} \right]_{x=0}^{x=3} \
&= \pi \left( \frac{27}{3} - \frac{0}{3} \right) \
&= 9\pi
\end{align*}
So the volume of the object is equal to 9π cubic units.
The table shows the input, x, and output, y, relationship for a function.
Which function rule describes the relationship between x and y?
f(x)=13x−1
f(x)=−13x−1
f(x)=3x+1
f(x)=3x−1

Answers
f(x) = 1/3x -1
I am not sure if it is right but I am 90% sure
Answer: f(x)=1/3x-1
Step-by-step explanation:
attached is full test answers
hope this can help someone

9. Put these numbers in greatest to least order: 2/3, 60%, 0.06, 3/4
Answers
Step-by-step explanation:
0.0660%2/33/4hope it's right :)
Enter a positive value for d that makes this statement true: 34×d is less than 34 but greater than zero HELP PLSS FASTT
Answers
Answer:
0.5 (any number between 0 and 1)
Step-by-step explanation:
34 * 0.5 = 17
34 > 17 > 0
In your own words, explain what it means for a shape to be symmetrical.
Answers
f(x) = 3sinxº
Find f(22)
Give your answer correct to 3 significant figures.
Answers
Answer:
f(22) = 1.12
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightAlgebra I
Function NotationStep-by-step explanation:
Step 1: Define
f(x) = 3sinx°
f(22) is x = 22
Step 2: Evaluate
Substitute in x: f(22) = 3sin22°Trig: f(22) = 3(0.374607)Multiply: f(22) = 1.12382Round: f(22) = 1.12can someone please help? the question is in the picture.

Answers
Answer: b
Step-by-step explanation: a right triangle should have a right angle so you´d need atleast one right angle and two acute angles.
Need answer 25 and answer 27

Answers
\(\\ \bull\tt\dashrightarrow \dfrac{-3}{8}x-20+2x>6\)
\(\\ \bull\tt\dashrightarrow \dfrac{-3}{8}x+2x=6+20=26\)
\(\\ \bull\tt\dashrightarrow \dfrac{-3+16}{8}x=26\)
\(\\ \bull\tt\dashrightarrow \dfrac{13}{8}x=26\)
\(\\ \bull\tt\dashrightarrow x=26\times \dfrac{8}{13}\)
\(\\ \bull\tt\dashrightarrow x=8(2)=16\)
#27
\(\\ \bull\tt\dashrightarrow 0.5x-4-2x\leqslant 2\)
\(\\ \bull\tt\dashrightarrow 0.5x-2x\leqslant=2+4=6\)
\(\\ \bull\tt\dashrightarrow -1.5x\leqslant 6\)
\(\\ \bull\tt\dashrightarrow x\leqslant\dfrac{6}{-1.5}\)
\(\\ \bull\tt\dashrightarrow x\leqslant 4\)
The U.S. Department of Agriculture reported that out of every milk drinkers drink skim milk. If a storeowner orders gallons of milk, how many should be skim? Round the answer to the nearest gallon. To supply all of the skim milk drinkers, out of the gallons of milk ordered, gallons were skim milk.
Answers
Complete Question
The complete question is shown on the first uploaded image
Answer:
The value is \(s = 12 \ gallons\)
Step-by-step explanation:
From the question we are told that
The number of milk drinkers considered is \(m = 100\)
The number of skim milk drinkers \(n = 50\)
The gallons of milk supplied is q = 23 gallons
Generally the proportion of skim milk drinkers is mathematically represented as
\(p = \frac{n}{m}\)
\(p = 0.5\)
Generally the gallons of milk order that is skim milk is mathematically represented as
\(s = 0.5 * 23\)
=> \(s = 12 \ gallons\)

One brand of cola co fizz is sold in packs of 4*500ml for 2.50 another brand colo is sold in packs of 10 330mlfo $2 which brand is more expensive
Answers
Based on the given information, the second brand, Cola, is the more affordable option in terms of cost per milliliter compared to Co Fizz.
To determine which brand of cola is more expensive, we need to compare the cost per unit volume for each brand.
For the first brand, Co Fizz, a pack contains 4 bottles, and each bottle has a volume of 500 ml. The cost of the pack is $2.50. Therefore, the total volume in a pack is 4 * 500 ml = 2000 ml. To find the cost per milliliter (ml), we divide the total cost by the total volume: $2.50 / 2000 ml = $0.00125 per ml.
For the second brand, Cola, a pack contains 10 bottles, and each bottle has a volume of 330 ml. The cost of the pack is $2. Therefore, the total volume in a pack is 10 * 330 ml = 3300 ml. To find the cost per milliliter (ml), we divide the total cost by the total volume: $2 / 3300 ml ≈ $0.000606 per ml.
Comparing the two brands, we can see that the cost per milliliter for Co Fizz is $0.00125, while the cost per milliliter for Cola is approximately $0.000606.
Since the cost per milliliter for Co Fizz is higher than the cost per milliliter for Cola, it can be concluded that Co Fizz is more expensive in terms of price per unit volume.
For more such question on brand. visit :
https://brainly.com/question/29129317
#SPJ8
daniel found a job in the classified ads that pays a yearly salary of $88.7k. What is the bi-weekly salary based on this annual salary
Answers
Answer:
$3,695.83 bi-weekly
Step-by-step explanation:
$88.7k divided by 12 (the months of the year)which comes $7,391.67then divide by 4 (weeksof the month)which comes $1,847.91because it says bi-weekly (2 weeks)multiply by 2 then final answer will be = $3,695.83A plane flying horizontally at an altitude of 1 mile and a speed of 480 mi/h passes directly over a radar station. Find the rate at which the distance from the plane to the station is increasing when it has a total distance of 5 miles away from the station. (Round your answer to the nearest whole number.)
Answers
Answer:
to the nearest whole number, we get:
dd/dt ≈ 490 miles per hour
Step-by-step explanation:
Let's call the distance between the plane and the radar station "d". We want to find the rate at which this distance is increasing when the total distance between the plane and the station is 5 miles.
We can use the Pythagorean theorem to relate the distance d to the altitude h of the plane:
d^2 = h^2 + x^2
where x is the horizontal distance the plane has traveled from directly above the station.
Taking the derivative of both sides with respect to time t, we get:
2d * dd/dt = 2h * dh/dt + 2x * dx/dt
where dd/dt is the rate at which the distance between the plane and the station is changing, and dh/dt and dx/dt are the rates at which the altitude and horizontal distance are changing, respectively.
At the moment when the plane is 5 miles away from the station, we have:
d = 5 miles
h = 1 mile (since the plane is flying at an altitude of 1 mile)
dx/dt = 480 mi/h (since the plane is flying horizontally at a speed of 480 mi/h)
We want to find dd/dt, the rate at which the distance between the plane and the station is increasing. We can solve for dd/dt by plugging in the given values and solving for it:
2d * dd/dt = 2h * dh/dt + 2x * dx/dt
2(5 miles) * dd/dt = 2(1 mile) * 0 + 2x * (480 mi/h)
10 * dd/dt = 960 * x
We still need to find x, the horizontal distance traveled by the plane when it is 5 miles away from the station. We can use the Pythagorean theorem again:
d^2 = h^2 + x^2
(5 miles)^2 = (1 mile)^2 + x^2
x^2 = (5 miles)^2 - (1 mile)^2
x = √(24 miles^2)
x = 4.899 miles (rounded to three decimal places)
Now we can plug in the value of x and solve for dd/dt:
10 * dd/dt = 960 * x
10 * dd/dt = 960 * 4.899
dd/dt = 489.9 (rounded = 490)
A school has 320 girls and 250 boys
The probability that a girl is left handed is 0.2
The probability that a boy is left handed is 0.1
Estimate the umber of left handed students in the school.
Answers
250/100 • 10 = 25
64+25= 89 <33
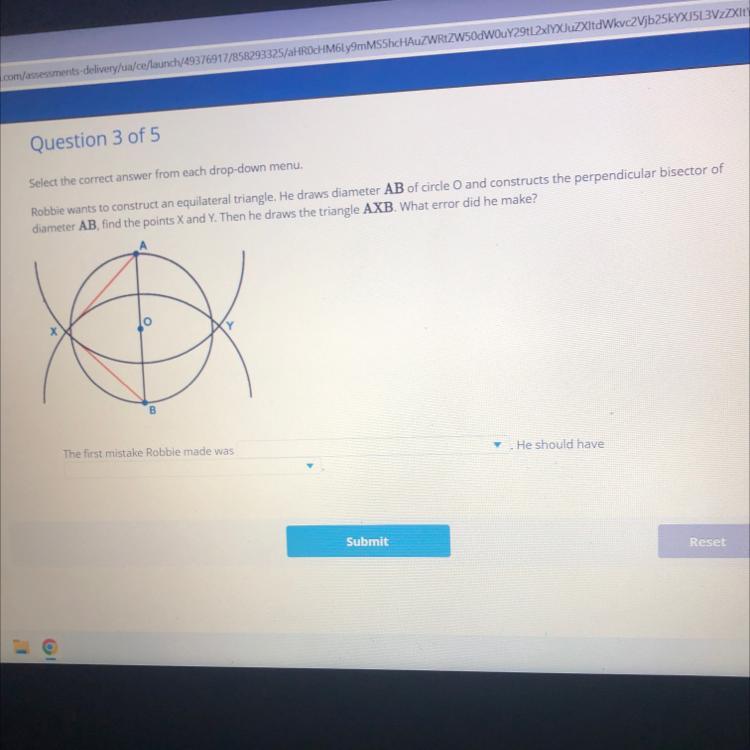
Select the correct answer from each drop-down menu.
Robbie wants to construct an equilateral triangle. He draws diameter AB of circle O and constructs the perpendicular bisector of
diameter AB, find the points X and Y. Then he draws the triangle AXB. What error did he make?
The first mistake Robbie made was
Submit
.He should have
Reset
Answers
The first mistake Robbie made was, take improper lengths. AB is the diameter; its length is longer than the sides AX and XB. So, the triangle formed will not be an equilateral triangle.
What is an equilateral triangle?An equilateral triangle in geometry is a triangle with equally long sides. The three angles opposing the three equal sides are equal in size because the three sides are equal.
The first mistake Robbie made was, take improper lengths. AB is the diameter; its length is longer than the sides AX and XB. So, the triangle formed will not be an equilateral triangle.
He should have, after drawing the diameter AB, construct a circle with point A as the center and AO as the radius. Mark the point of intersection as X. Then, AO, AX and OX would form an equilateral triangle.
Learn more about equilateral triangle here:
https://brainly.com/question/3461022
#SPJ1
Answer:
1. constructing the perpendicular bisector of AB
2.
Step-by-step explanation:
A beverage manufacturer performs a taste-test and discovers that people like their fizzy beverages best when the radius of the bubbles is about 0.3 mm. According to the formula below, what would be the volume of one of these bubbles? r = root(3, (3V)/(4s))

Answers
V = 4(3.14) (0.3)³ / 3
V = 0.11 mm³
Option A
the radius r of the circle below is 11cm

Answers
Answer:
\({ \bf{area = \pi {r}^{2} }} \\ = 3.14 \times {11}^{2} \\ = 380.1 \: {cm}^{2} \)
Step 1: Rewrite equation
As the first step, it is helpful to rewrite the equation for the area of a circle. The a will stand for area, the π will stand for pi, and the r will stand for radius.
a= πr²
Step 2: Substitute numbers
For step 2, we will substitute information. We are made aware that the radius is 11, so we will replace r with 11. To make the equation easier to understand, we will add the multiplication sign in between pi and 11 squared.
a= π•11²
Step 3: Solve using PEMDAS
To solve this equation, we will follow the order of operations, also referred to as PEMDAS, standing for parentheses-exponent-multiplication-division-addition-subtraction. According to this formula, the first thing we will need to do is solve for the exponent. To do so, let’s find the squared value of 11.
a= π•11²
a= π•121
For the next part, we need to multiply 121 by π for the final answer. For the sake of this problem, we will leave pi as 3.14. This can always be replaced by putting the pi symbol into your calculator, though we will use 3.14.
a= 3.14•121
a= 379.94
This is your answer. Hope this helps! Comment below for more questions.
PLease help me and answer the questions in the picture below you will make my day!


Answers
Answer:
b the solution is (3,5)
Step-by-step explanation:
look at the points where the lines intersect
what is the range of magazines sold?
please answer will give brainliest

Answers
Answer:
range: 8
Step-by-step explanation:
In order to find the range you need the minimum and maximum
minimum: 17
maximum: 25
Subtract
25-17=8
___ ÷ 8 + 9 = 16
Find missing number
Answers
Answer:
56
Step-by-step explanation:
Answer: 56
Step-by-step explanation:
First, you can set up the problem algebraically like this:
\(\frac{x}{8}+9=16\)
Then, subtract 9 from both sides:
\(\frac{x}{8}+9=16\)
-9 -9
\(\frac{x}{8}=7\)
Finally, multiply both sides by 8 and you get:
\(\frac{x}{8}=7\)
×8 ×8
\(x=56\)
Therefore, the missing number is 56.
I hope this helps!
Southside High School found that 80% of last year's sold-out plays occurred
during weekend performances. Based on this information, the drama teacher
decided to add another performance time on Saturday. This decision is a
result of
OA. describing data
OB. making an inference
OC. creating involvement
D. collecting data
Answers
Answer:
B. making an inference.
Step-by-step explanation:
The drama teacher's decision to add another performance time on Saturday is a result of making an inference based on the information that 80% of last year's sold-out plays occurred during weekend performances. By observing this pattern, the drama teacher infers that adding another performance on Saturday will likely attract a larger audience and increase the chances of having a sold-out show.
1) Write an equation in slope-intercept form of the line with slope of 6 and y-intercept of -3. Then graph the line. 2) Write an equation in point-slope form of the line with slope -3/5 that contains(-10 ,8). Then graph the line.
Answers
Answer:
An equation in the slope-intercept form is:
y = a*x + b
Where a is the slope, and b is the y-intercept.
a)
Here we have a slope of 6 and a y-intercept of -3
Then the equation is:
y = 6*x - 3
Now we want to graph this.
To graph it, we first need to find two points (x, y) that belong to this equation, then we can graph the points, and connect them with a line.
To find the points, we evaluate in two different values of x.
x = 0
y = 6*0 - 3 = -3
Then we have the point (0, -3)
x = 1
y = 6*1 - 3 = 3
Then we have the point (1, 3)
The graph of this line can be seen in the image below (the red one)
b) Similar to before, here the slope is -3/5, then the equation is something like:
y = (-3/5)*x + b
Now we also know that the line passes through the point (-10, 8)
This means that when x = -10, we must have y = 8
Replacing these two in the equation we get:
8 = (-3/5)*-10 + b
8 = 6 + b
8 - 6 = 2 = b
Then this equation is:
y = (-3/5)*X + 2
The graph can be found in the same way as before, the graph of this function can also be seen in the image below (the green one)

Four friends are playing a game. 36 cards are dealt out between the friends. Which equation can be used to find how many cards each person receives
Answers
Given
Four friends are playing a game.
36 cards are dealt out between the friends.
To find: Which equation can be used to find how many cards each person receives.
Explanation:
It is given that,
Four friends are playing a game.
36 cards are dealt out between the friends.
Let x be the number of cards received by each person.
Then,
\(\begin{gathered} 4x=36 \\ x=\frac{36}{4} \\ x=9 \end{gathered}\)Hence, each person receives 9 cards.
Thus,
\(undefined\)HELP 10 POINT FOR THIS EQUATION!
Combine the like terms to create an equivalent expression.
12p+p
Answers
Answer:The equivalent expression of the given terms is 13p
