Answers
Answer:
i think the green line would be the horizontal asymptote cause its like horizontal amd it goes across the graph.
Step-by-step explanation:
Related Questions
A coin is flipped, and a number cube is rolled. what is the probability of getting tails on the coin and an even number on the number cube?
Answers
The probability of getting tails on the coin and an even number on the number cube is 1/4
What are probabilities?Probabilities are used to determine the chances, likelihood, possibilities of an event or collection of events
How to determine the probability?The sample space of a coin is:
S = {H, T}
The sample space of a die is:
S = {1, 2, 3, 4, 5, 6}
The above means that:
A coin has 2 faces, one of which is the tail.
So, we have:
P(Tail) = 1/2
A number cube has 6 numbers, 3 or which are even.
So, we have
P(Even) = 3/6
The required probability is
P = P(Tail) * P(Even)
This gives
P = 1/2 * 3/6
Evaluate
P = 1/4
Evaluate the quotient
P = 0.25
Hence, the probability of getting tails on the coin and an even number on the number cube is 1/4 or 0.25
Read more about probability at:
https://brainly.com/question/11234923
#SPJ1
Consider the following data set. Round your answers to the nearest hundredth as needed.83 91 104 72 97118 118 118 8996Mean =Median =Mode =Range =Sample Standard Deviation =Check Answer
Answers
Arrange the data in ascending order,
\(72,83,89,91,96,97,104,118,118,118\)The mean is ,
\(x=\frac{72+83+89+91+96+97+104+118+118+118}{10}\)\(x=\frac{986}{10}\)\(x=98.6\)The mean is 98.6.
The median is,
\(M=\frac{(\frac{n}{2})th+(\frac{n}{2}+1)th}{2}\)\(M=\frac{(\frac{10}{2})th+(\frac{10}{2}+1)th}{2}\)\(M=\frac{96+97}{2}\)\(M=\text{ 96.5}\)The median is 96.5.u
The mode is the value that appears most often in a set of data values.
\(m=\text{ 118}\)The range is determined as the difference between the maximum and minimum value.
\(R=118-72\)\(R=\text{ 46}\)Express the formula d=rt in terms of the time,t. Use your formula to find the time when the distance is 40 and the rate is 8.
Answers
The expression for d=rt in terms of the time is t = d/r; t = 5.
What is time? Time can be defined as a continuous and ongoing sequence of events that occur consecutively from the past to the present to the future. Time is used to measure, measure or compare the duration of events or the intervals between them, and even the sequence of events. Time is a useful concept that we use in our daily life. We have to watch when we cook, play, study, go to school, meet someone, etc. So knowing the right time is very important. Time is usually the answer to when an event happens or happened. The concept of time determines when a certain event occurs, has occurred or will occur. Time is a measurable quantity and is also infinite. The time is calculated in seconds, minutes, hours, days, months and years.Therefore,
In the equation d=rt
t = d/r
when distance is 40 and the rate is 8
t = d/r
Replace d with 40 and rate with 8
t = 40/8
t = 5
To learn more about time, refer;
https://brainly.com/question/28050940
#SPJ1
In Exercises 43 through 46, solve the given separable initial value problem. 43. dx/dy =−2y;y=3 when x=0 44. dx/dy =xy;y=1 when x=0 45. dx/dy = e^x+y
;y=0 when x=0 46. dx/dy = √(y/x);y=1 when x=1
Answers
The solution to the initial value problem is √x = (1/3) \(y^{\frac{3}{2} }\) + 2/3.
Given: dx/dy = -2y, y = 3 when x = 0
To solve this, we'll separate the variables and integrate:
dx = -2y dy
Integrating both sides:
∫ dx = ∫ -2y dy
x = - \(y^{2}\) + C
Now we can apply the initial condition y = 3 when x = 0:
0 = - \(3^{2}\) + C
C = -9
Therefore, the solution to the initial value problem is x = - \(y^{2}\) - 9.
Given: dx/dy = xy, y = 1 when x = 0
We'll again separate the variables and integrate:
dx = xy dy
Integrating both sides:
∫ dx = ∫ xy dy
x = (1/2)\(y^{2}\) + C
Applying the initial condition y = 1 when x = 0:
0 = (1/2) \(1^{2}\) + C
C = -1/2
Thus, the solution to the initial value problem is x = (1/2)\(y^{2}\) - 1/2.
Given: dx/dy = \(e^{x+y}\), y = 0 when x = 0
Separating the variables and integrating:
dx = \(e^{x+y}\) dy
∫ dx = ∫ \(e^{x+y}\) dy
x = \(e^{x+y}\) + C
Using the initial condition y = 0 when x = 0:
0 = \(e^{0+0}\) + C
C = -1
Hence, the solution to the initial value problem is x = \(e^{x+y}\) - 1.
Given: dx/dy = √(y/x), y = 1 when x = 1
Again, separating the variables and integrating:
dx/√x = √y dy
Integrating both sides:
2√x = (2/3)\(y^{\frac{3}{2} }\) + C
Simplifying:
√x = (1/3)\(y^{\frac{3}{2} }\) + C
Applying the initial condition y = 1 when x = 1:
1 = (1/3)\(1^{\frac{3}{2} }\) + C
C = 2/3
Therefore, the solution to the initial value problem is √x = (1/3) \(y^{\frac{3}{2} }\) + 2/3.
To learn more about exponent, refer:-
brainly.com/question/30066987
#SPJ4
Two people are trying to raise an object from a hole using two ropes, as shown in the diagram below. Person 1 exerts a force of
355 N and Person 2 exerts a force of 425 N.
What is the magnitude of the combined force applied by both people?

Answers
Answer:
554 N
Step-by-step explanation:
We're looking for the magnitude of the force - angles don't matter.
We need to resolve the two forces.
As you can see in the attached drawing, this basically just becomes Pythagoras.
\( {f}^{2} = {355}^{2} + {425}^{2}\)
\(f = \sqrt{ {355}^{2} + {425}^{2} } \)
\(f = 553.76\)

A control chart is a visual representation of the various states in a process O a False O b. True
Answers
A control chart is a visual representation of the various states in a process. The answer is b. True. Control charts are used in quality control and process improvement to monitor and analyze the performance of a process over time.
b. True. A control chart is a graphical tool used to monitor the performance of a process over time. It is a visual representation of the data collected from the process and helps in identifying any patterns or trends that may occur. The chart typically consists of a central line representing the average or target value, and upper and lower control limits representing the acceptable range of values for the process. The data is plotted on the chart, and any points that fall outside the control limits indicate a process that is out of control and may require further investigation. Control charts are commonly used in industries such as manufacturing, healthcare, and finance to ensure that processes are running smoothly and to identify any potential issues early on. Overall, control charts provide a powerful way to monitor and manage processes in a systematic manner.
They help to identify trends, patterns, and variations that may indicate potential issues, allowing for timely corrective actions to be taken.
To know more about Chart visit:
https://brainly.com/question/30387848
#SPJ11
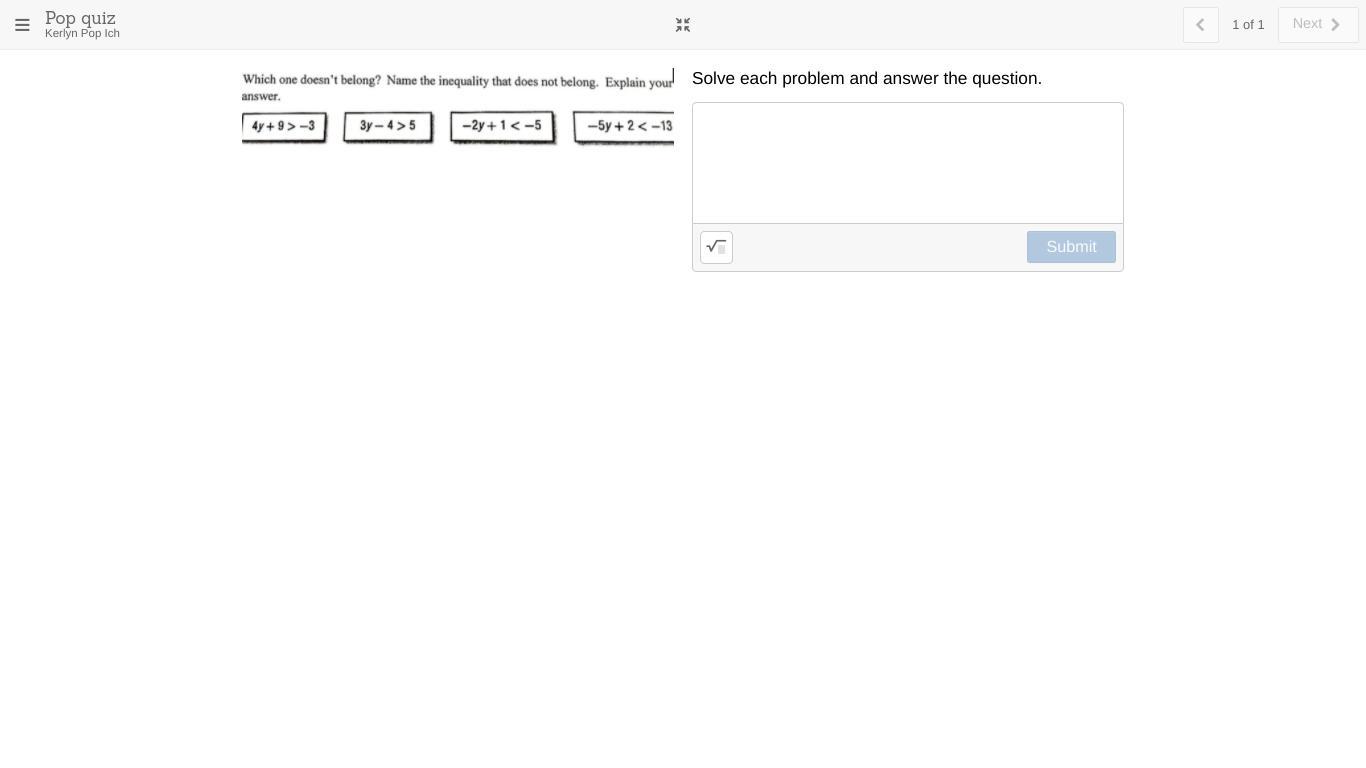
Solve each problem and answer the question.plz help me
Answers
Grant plans to evaporate enough water from 22 gallons of a 16% ammonia solution to make a 24% ammonia solution. Which equation can he use to find n, the number of gallons of water he should remove?
3.52 (22 minus n) = 0.24
StartFraction 22 minus n Over 3.52 EndFraction = StartFraction 24 Over 100 EndFraction
StartFraction 3.52 Over 22 minus n EndFraction = StartFraction 24 Over 100 EndFraction
3.52 + (22 minus n) = 0.24
Answers
The equation that he used to find n, the number of gallons of water he should remove is 3.52 / (22 - n) = 24 / 100. Option C is correct.
Functions are the relationship between sets of values. e g y=f(x), for every value of x there is its exists in a set of y. x is the independent variable while Y is the dependent variable.
Amount of ammonia in the solution 16% x 22 gallons = 3.52 gallons
The proportion of ammonia remains the same as the water evaporates, but the total composition of the solution is decreased by the amount of water that evaporates.
Quantity of ammonia = 3.52 gallons
Quantity of water after evaporation = 22 - n
Composition of ammonia after evaporation of water, 24% = 24/100
Now the percentage of ammonia after evaporates
Quantity of ammonia / Remaining water = 24%
3.52 / (22 - n) = 24 / 100
Thus, the equation that he used to find n, the number of gallons of water he should remove is 3.52 / (22 - n) = 24 / 100.
Learn more about function here:
brainly.com/question/21145944
#SPJ1
please answer this 3 questions quickly
Find the area of the region below y = x2 + 2x – 2 and above y = 5 for 2
Answers
To find the area of the region below the curve y = x^2 + 2x - 2 and above the line y = 5, we need to determine the intersection points of the two curves and then calculate the area between them.
Step 1: Find the intersection points. Set the two equations equal to each other: x^2 + 2x - 2 = 5. Rearrange the equation to bring it to the standard quadratic form: x^2 + 2x - 7 = 0. Solve this quadratic equation for x using factoring, completing the square, or the quadratic formula. Let's use the quadratic formula:x = (-2 ± √(2^2 - 41(-7))) / (2*1)
x = (-2 ± √(4 + 28)) / 2
x = (-2 ± √32) / 2
x = (-2 ± 4√2) / 2
x = -1 ± 2√2. So the two intersection points are: x = -1 + 2√2 and x = -1 - 2√2. Step 2: Calculate the area. To find the area between the two curves, we integrate the difference between the two curves with respect to x over the interval where they intersect.
The area can be calculated as follows: Area = ∫[a, b] (f(x) - g(x)) dx. In this case, f(x) represents the upper curve (y = x^2 + 2x - 2) and g(x) represents the lower curve (y = 5). Area = ∫[-1 - 2√2, -1 + 2√2] [(x^2 + 2x - 2) - 5] dx. Simplify the expression: Area = ∫[-1 - 2√2, -1 + 2√2] (x^2 + 2x - 7) dx. Integrate the expression: Area = [(1/3)x^3 + x^2 - 7x] evaluated from -1 - 2√2 to -1 + 2√2. Evaluate the expression at the upper and lower limits:Area = [(1/3)(-1 + 2√2)^3 + (-1 + 2√2)^2 - 7(-1 + 2√2)] - [(1/3)(-1 - 2√2)^3 + (-1 - 2√2)^2 - 7(-1 - 2√2)]. Perform the calculations to obtain the final value of the area. Please note that the calculations involved may be quite lengthy and involve simplifying radicals. Consider using numerical methods or software if you need an approximate value for the area.
To learn more about curve click here: brainly.com/question/31849536
#SPJ11
Find the average rate of change of f(x) = -11√x + 14 over the interval [-10, -9].
Write your answer as an integer, fraction, or decimal rounded to the nearest tenth. Simplify
any fractions.
Answers
The average rate of change of f(x) = -11√x + 14 over the interval [-10, -9]. is 0.7
What is the average rate of change?The average Rate of Change of the function f(x) can be calculated as;
\(f(x) = \dfrac{f(b) - f(a)}{b-a}\)
We have been given the function as; f(x) = -11√x + 14 over the interval [-10, -9].
i.e. a = -10 and b = -9
Therefore, f(x) = -11√x + 14
f(-9) = -11√(-9) + 14
f(-9) = -33 + 14
f(-9) = -19
Also, f(-10) = -11√(-10) + 14
f(-10) = - 34.7 + 14
f(-10) = 20.7
Now, substitute the values;
\(f(x) = \dfrac{f(b) - f(a)}{b-a}\\f(x) = \dfrac{f(-9) - f(-10)}{-9+ 10}\\f(x) = \dfrac{-19-20.7}{1}\\f(x) = 0.7\)
Hence, the average rate of change of f(x) = -11√x + 14 over the interval [-10, -9]. is 0.7
Learn more about average rate;
https://brainly.com/question/20784578
#SPJ1
The question is in the photo, I thought they were all wrong, so I am super confused. Whoever proves me wrong gets 15 points.
Please make sure you know what you are doing before you answer.

Answers
If the steps are shaped like rectangular prism, then the expression that can be used to find the volume is option (B) (6×16×6)+(14×16×7)
The steps are shaped like rectangular prism
The length of the rectangular prism = l×w×h
Where l is the length
w is the width
h is the height
First we have to separate the given steps in to two rectangular prism and find the volume of each prism
The volume of the top prism = l×w×h
= 6×16×6 cubic inches
The volume of the bottom prism = l×w×h
= 14×16×7 cubic inches
The total volume = (6×16×6)+(14×16×7) cubic inches
Hence, if the steps are shaped like rectangular prism, then the expression that can be used to find the volume is option (B) (6×16×6)+(14×16×7)
Learn more about volume here
brainly.com/question/21308574
#SPJ1

Using the equation y = 8x , what would y be if x = 2

Answers
Answer:
Y=16
Step-by-step explanation:
Becasue if you substitute 2 in for x, you get 8 times 2=16
Answer:
y=8 and
x=2
If x=2, then
8x=8*2=16
so therefore , y=8x i.e 16
y=16
SIMPLE AS THAT !!
Step-by-step explanation:
let p and q be distinct primes. (1) prove that (z/(pq))× has order (p − 1)(q − 1);
Answers
The order of a in (z/(pq))× is exactly (p-1)(q-1), as desired.
To prove that (z/(pq))× has order (p − 1)(q − 1), we need to show that the least positive integer n such that (z/(pq))×n = 1 is (p − 1)(q − 1).
First, let's define (z/(pq))× as the set of all integers a such that gcd(a,pq) = 1 (i.e., a is relatively prime to pq) and a mod pq is also relatively prime to pq.
Now, we know that the order of an element a in a group is the smallest positive integer n such that a^n = 1. Therefore, we need to find the order of an arbitrary element a in (z/(pq))×.
Let's assume that a is an arbitrary element in (z/(pq))×. Since gcd(a,pq) = 1, we know that a has a multiplicative inverse modulo pq, denoted by a^-1. Therefore, we can write:
a * a^-1 ≡ 1 (mod pq)
Now, let's consider the order of a. Since gcd(a,pq) = 1, we know that a^(p-1) is congruent to 1 modulo p by Fermat's Little Theorem. Similarly, we can show that a^(q-1) is congruent to 1 modulo q. Therefore, we have:
a^(p-1) ≡ 1 (mod p)
a^(q-1) ≡ 1 (mod q)
Now, we can use the Chinese Remainder Theorem to combine these congruences and get:
a^(p-1)(q-1) ≡ 1 (mod pq)
Therefore, we know that the order of a must divide (p-1)(q-1).
To show that the order of a is exactly (p-1)(q-1), we need to show that a^k is not congruent to 1 modulo pq for any positive integer k such that 1 ≤ k < (p-1)(q-1).
Assume for contradiction that there exists such a k. Then, we have:
a^k ≡ 1 (mod pq)
This means that a^k is a multiple of pq, which implies that gcd(a^k, pq) ≥ pq. However, since gcd(a,pq) = 1, we know that gcd(a^k, pq) = gcd(a,pq)^k = 1. This is a contradiction, and therefore our assumption must be false.
Know more about prime here:
https://brainly.com/question/20532807
#SPJ11
The order of a in (z/(pq))× is exactly (p-1)(q-1), as desired.
To prove that (z/(pq))× has order (p − 1)(q − 1), we need to show that the least positive integer n such that (z/(pq))×n = 1 is (p − 1)(q − 1).
First, let's define (z/(pq))× as the set of all integers a such that gcd(a,pq) = 1 (i.e., a is relatively prime to pq) and a mod pq is also relatively prime to pq.
Now, we know that the order of an element a in a group is the smallest positive integer n such that a^n = 1. Therefore, we need to find the order of an arbitrary element a in (z/(pq))×.
Let's assume that a is an arbitrary element in (z/(pq))×. Since gcd(a,pq) = 1, we know that a has a multiplicative inverse modulo pq, denoted by a^-1. Therefore, we can write:
a * a^-1 ≡ 1 (mod pq)
Now, let's consider the order of a. Since gcd(a,pq) = 1, we know that a^(p-1) is congruent to 1 modulo p by Fermat's Little Theorem. Similarly, we can show that a^(q-1) is congruent to 1 modulo q. Therefore, we have:
a^(p-1) ≡ 1 (mod p)
a^(q-1) ≡ 1 (mod q)
Now, we can use the Chinese Remainder Theorem to combine these congruences and get:
a^(p-1)(q-1) ≡ 1 (mod pq)
Therefore, we know that the order of a must divide (p-1)(q-1).
To show that the order of a is exactly (p-1)(q-1), we need to show that a^k is not congruent to 1 modulo pq for any positive integer k such that 1 ≤ k < (p-1)(q-1).
Assume for contradiction that there exists such a k. Then, we have:
a^k ≡ 1 (mod pq)
This means that a^k is a multiple of pq, which implies that gcd(a^k, pq) ≥ pq. However, since gcd(a,pq) = 1, we know that gcd(a^k, pq) = gcd(a,pq)^k = 1. This is a contradiction, and therefore our assumption must be false.
Know more about prime here:
https://brainly.com/question/20532807
#SPJ11
Amir is laying stone for his new patio. The diagram of the patio is shown. How many
square feet of stone does Amir need to cover on his patio?

Answers
Answer: 108ft^2
Step-by-step explanation:
First, at the top we have two triangle rectangles.
The area of a triangle rectangle is equal to the product of their cathetus divided by two.
We know that one common cathetus for both triangles is 6ft.
And both share the bottom line that is 14ft long, so half of that corresponds to each triangle.
14ft/2 = 7ft
Then each triangle has a cathetus of 6ft and one of 7ft.
Then the area of each triangle rectangle at the top is:
6ft*7ft/2 = 21ft^2
And we have two of them, so the area for now is:
A1 = 21ft^2 + 21ft^2 = 42ft^2.
Now let's look at the bottom part, we can divide this into two triangle rectangles and one rectangle.
First, bottom side is 8ft, then the difference between this side and the 14ft one is:
14ft - 8ft = 6ft
(We calculate this because we are making a rectangle, then the bottom side length must be equal than the top one).
Then we have a surpass of 6ft, which we will divide into both triangle rectangles (3ft for each, this is one of the cathetus).
And we can see that the cathetus shown of this triangle rectangle is 6ft (this is also the other side of our rectangle)
Then we have two triangles with cathetus 6ft and 3 ft, the area is:
A = 6ft*3ft/2 = 9ft^2
And we have two of them, then A2 = 18ft^2.
And the rectangle is 8ft by 6ft, the area is:
A3 = 8ft*6ft = 48ft^2
Then if we add all the areas that we found, we have:
A1 + A2 + A3 = 42ft^2 + 18ft^2 + 48ft^2 = 108ft^2
How many inches in 900 mm?
Answers
900 millimeters is equivalent to 35.433070866 inches.
Inches and millimeters are both units of measurement for length. To convert from millimeters to inches, we can use the conversion factor that 1 inch is equal to 25.4 millimeters. To convert 900 millimeters to inches, we can multiply 900 by the conversion factor.
The formula for converting millimeters to inches is:
inches = millimeters / 25.4
So in this case:
inches = 900 / 25.4
After doing the calculation, we find that 900 millimeters is equivalent to 35.433070866 inches.
It's important to note that the conversion factor is a constant value which is used multiple times during the conversion process.
to know more about inches refer here
https://brainly.com/question/16311877#
#SPJ11
PLS HELP I WILL GIVE BRAINLIEST.

Answers
=25cm^2
The population of a 24-storey building is 600 persons. The contract speed of each lift is 4 m/s. The client intends to achieve an up peak interval of not more than 32 s with the expected up peak demand not less than 20%. The inter-floor height is 8 m. The door opening time is 2 s. The door closing time is 2 s The passenger loading time is 0.8 s. The passenger unloading time is 0.8 s. The single floor flight time is 5 s. Determine: (a) the minimum up-peak handling capacity (UPPHC); (b) the minimum contract capacity (CC); ): (C) the average highest call reversal floor (H) and the average number of stops (S); (d) the round trip time (RTT); (e) the number of lift required (L); and (f) the real up peak interval (UPPINT). Hence, comment whether the quality of the lift system is excellent acceptable or others.
Answers
The given data are:N = 600; G = 24; S = 4 m/s; Up-peak interval = 32 s; Expected up-peak demand = 20%; h = 8 m; Door opening time = 2 s; Door closing time = 2 s; Passenger loading time = 0.8 s;
Passenger unloading time = 0.8 s; Single floor flight time = 5 s; Hence, the minimum up-peak handling capacity (UPPHC) is 20% of 600 persons as per the question. Thus, UPPHC = (20/100) × 600=120 persons.
(a) Minimum up-peak handling capacity (UPPHC): UPPHC = 120 persons.
(b) Minimum contract capacity (CC): The formula for CC is given byCC = [(UPPHC × 3600)/Up-peak hours] = [(120 × 3600)/4] = 10800 persons/hr.
Hence, the minimum contract capacity is 10800 persons/hr.
(c) Average highest call reversal floor (H) and the average number of stops (S):
The formula for the average highest call reversal floor isH = [n/(n – 1)] × [∑f/(n × P)].
Where, n = number of lifts; ∑f = sum of the products of the number of floors served and the corresponding number of calls; and P = ∑f/number of floors served. Thus, H = [n/(n – 1)] × [∑f/(n × P)]For S, the formula is given by
S = ∑f/(n × P).
Thus, for calculating H and S, the traffic calculation is done, and the calculations are provided below:
For traffic design, let n = 3. Then, Np = UPPHC/up-peak hour= (120 × 3600)/3600=120 persons/hr.
Let the average number of stops be S. Then the number of floors served on the average during the up-peak hour is given by 24/S.
From the traffic flow diagram, the average highest call reversal floor is (3/2) H
= [3/(3 – 1)] × [((1 × 2) + (2 × 4) + (3 × 7) + (4 × 8) + (5 × 9) + (6 × 10) + (7 × 10) + (8 × 9) + (9 × 8) + (10 × 7) + (11 × 6) + (12 × 5) + (13 × 4) + (14 × 2))/(3 × 12)] = (3/2) × 7.63 = 11.45 ≈ 11 th floor.
∴ Average highest call reversal floor, H = 11th floor.∴ The average number of stops,
S = ∑f/(n × P)= [(1 × 2) + (2 × 4) + (3 × 7) + (4 × 8) + (5 × 9) + (6 × 10) + (7 × 10) + (8 × 9) + (9 × 8) + (10 × 7) + (11 × 6) + (12 × 5) + (13 × 4) + (14 × 2)]/3 × 12 × 1= 526/36= 14.61 ≈ 15.
(d) Round trip time (RTT):The formula for RTT is given by RTT = 2 × [L × (h/S) × Single floor flight time + Door open and closing time + Passenger loading and unloading time].
Where, L = number of lifts required to provide the UPPHC during the up-peak hour.
Thus, the calculation for L is done first as:
L = UPPHC/[(h/S) × Single floor flight time × 3600/up-peak hour]Now, substituting the given values in the above formula, we get,L = 120/[(8/4) × 5 × 3600/240] = 5 lifts(approx.)
Now, substituting the above value of L in the formula for RTT, we get
RTT = 2 × [5 × (8/4) × 5 + 2 + 0.8 + 0.8] = 94 s(approx.).Thus, the round trip time (RTT) is 94 s.
(e) Number of lifts required (L): We have already calculated the value of L, which is equal to 5 lifts.
(f) Real up peak interval (UPPINT):The formula for the real up-peak interval is given by:
Real up peak interval = (RTT × Number of cycles per hour)/(60 × Number of lifts required)Where the number of cycles per hour is given by 3600/RTT.
Hence, the value of the number of cycles per hour is equal to 3600/94, which is approximately equal to 38.298.
Now, substituting all the above values in the formula, we get
Real up peak interval = (94 × 38.298)/(60 × 5) = 30.06 s(approx.).Hence, the real up-peak interval (UPPINT) is 30.06 s.
The quality of the lift system is excellent since the real up-peak interval is less than the up-peak interval of 32 s, which was the expected value.
To know more about Round trip time :
brainly.com/question/30464961
#SPJ11
2 1/3 cups of flour
3/4 of a cup of chocolate chips
2/5 of a cup of chopped almonds
1 1/2 cups of brown sugar
3/8 of a cup of white sugar
1/2 of a teaspoon of salt
Eric wishes to triple the recipe. How much of each ingredients should he use? Select all that apply
A) 6 1/3 cups of flour
B) 1/6 of a teaspoon of salt
C) 1 1/8 cups of white sugar
D) 9/12 cup of chocolate chips
E) 6/5 cups of chopped almonds
F) 2 1/2 cups of brown sugar
Its more than one answer
Answers
Answer:
A: 6/13 cups of flour.
Step-by-step explanation:
what is the slope for a line that is parallel to the line y=2/5x-4
Answers
Answer:
2/5
Step-by-step explanation:
The slope of the line
y=2/5x-4
is 2/5 since it is in the form y = mx+b where m is the slope
Parallel lines have the same slope so a line that is parallel to y=2/5x-4 has a slope of 2/5
how many times greater is 800,000 than -4,000,000
Answers
Translate this phrase into an algebraic expression.
7 increased by twice Gail's height
Use the variable g to represent Gail's height.
Answers
Answer:
7+2g
Step-by-step explanation:
7 increased by means 7 +
twice Gali's height =2g
everything now becomes 7+2g
if p = 2-5 and q = 8x3 find 3p-q
Answers
Answer:
3p - q = 3(2-5) - (8x3) = -9 - 24 = -33. Therefore, 3p-q=-33.
PERFORMANCE TASK : “TRANSVERSAL CITY MAP”
This project will help you to demonstrate your knowledge of parallel lines, transversals and the angles that are created by them. You will be designing a city map using the guidelines listed below. Your map must be drawn on construction paper or poster board. Use a ruler to make your streets straight! Have a title for your map, and make it neat and organized! You will be graded on accuracy, creativity and neatness.
Guidelines:
1) There must be a title for your map.
2) Your city must have three streets that are parallel to each other and one street that intersects all three of the parallel streets. You must name all of these streets.
3) Your city has a hospital that is alternate exterior to the school that is in your city. Draw and name the hospital and the school.
4) The school and the drugstore are at corresponding locations. Draw and name the drugstore.
5) The drugstore and the pet shop are at vertical locations. Draw and name the pet shop.
6) The pet shop and the gas station are at alternate interior locations. Draw and name the gas station.
7) The hospital and the park are at same side exterior locations. Draw and name the park.
8) The gas station and the grocery store are at same side interior locations. Draw and name the grocery store.
9) The grocery store and the nail salon are at vertical locations. Draw and name the salon.
10) The nail salon and bank are at corresponding locations. Draw Target.
11) The bank and a fast food restaurant are at same side interior locations. Draw and name the fast food restaurant.
12) Your city has a mall that is in a corresponding location to the bookstore that is in your city. Draw and name the mall and the bookstore. (If you did all of the others correctly, then the bookstore and the mall only have one place to be located)
Answers
In constructing a transversal city map by applying the knowledge of transversal and parallel lines, a map named California City Map has been drawn as shown in the image attached below.
(See attachment).
Recall:
Parallel lines are straight lines that do not meet each other.Transversal line is a that run through two or more straight lines that are parallel.Special angles are formed when transversal intersects parallel lines, which are: corresponding angles, same-side interior angles, same-side exterior angles, alternate exterior and alternate interior angles, and vertical angles.Using the knowledge of all these, an map named, "California City Map" has been drawn as shown in the image attached below.
The details are as follows:
1. Title for the map is:
California City Map.2. The three streets that are parallel are:
Adams BoulevardBeverly DriveCarroll AvenueThe street (transversal) that intersects the three is:
Darlin Way3. St. Michael Hospital is alternate exterior to Baptist Model School
4. Baptist Model School and Living Well Drug Store are in corresponding locations to each other.
5. Living Well Drug Store and Vik Pet Store are at vertical locations.
6. Vik Pet Store and Elite Gas-station are at alternate interior locations.
7. St. Michael Hospital and Livingstone Park are at same-side exterior locations.
8. Elite Gas-station and Richie Grocery Store are at same-side interior locations.
9. Richie Grocery Store and Beautyjay Nail salon are at vertical locations.
10. Beautyjay Nail salon and Retro Bank Plc are at corresponding locations.
11. Retro Bank Plc and Tessy's Fast Food Restaurant are at same-side interior locations.
12. California City Mall and Remis Bookstore are at corresponding locations.
In summary, in constructing a transversal city map by applying the knowledge of transversal and parallel lines, a map named California City Map has been drawn as shown in the image attached below.
(See attachment).
Learn more here:
https://brainly.com/question/13207832

Help please asap this is ixl skill TL8
Who ever answers I’ll mark then brainliest

Answers
Answer:
To do this we will substitute each one in
6, 1 =
4(6) - 3(1) = 5
24 - 3 = 5
21 = 5
so its not that one
0,6 =
4(0) - 3(6) = 5
0 - 18 = 5
18 = 5 not that one!
5, 5 =
4(5) - 3(5) = 5
20 - 15 = 5
5 = 5
(5,5) is one of the solutions
-3, -4 =
4(-3) -3(-4) = 5
-12 + 12 = 5
0 = 5
not that one
-1, -3 =
4(-1) - 3(-3) = 5
-4 + 9 = 5
5 = 5
(-1, -3) is also a solution
-5, 3 =
4(-5) - 3(3) = 5
-20 - 9 = 5
-29 = 5
The two solutions are (-1,-3) and (5,5)
Step-by-step explanation:
pls answer to become the brainliest

Answers
Answer:
37.50 square centimeters
Step-by-step explanation:
The computation of the area of the sector is as follows:
As we know that
Area of the circle is
= πr^2
Since the radius is 10 cm so the area of total circle is
= 3.14 × 100
= 314
Also it is 360 degrees
So, the area of the sector is
= 135 ÷ 360 × 1200
= 37.50 square centimeters
max rides his scooter toward kim and then passes her at a constant speed. his distance in feet, d, from kim t seconds after he started riding his scooter is given by d
Answers
The distance, d, in feet from Kim t seconds after Max started riding his scooter is given by the equation d = st, where s is the constant speed at which Max is riding his scooter.
To find the distance, d, we need to multiply the speed, s, by the time, t. Since Max passes Kim at a constant speed, the distance he travels is directly proportional to the time elapsed.
Therefore, the equation d = st represents this relationship, where d is the distance, s is the speed, and t is the time.
The equation d = st allows us to calculate the distance, d, from Kim t seconds after Max started riding his scooter, provided we know the constant speed, s, at which Max is traveling. By multiplying the speed by the time, we can determine how far Max has traveled from Kim at any given moment. This equation assumes that Max maintains a constant speed throughout his journey and that the speed does not change.
To know more about Distance, visit
https://brainly.com/question/30395212
#SPJ11
Maybe, I'm already gone
I'll never be the same
It hit me like a hurricane
It hit me like a tidal wave
And I don't know why I drown my mind in everything they say
It hit me like a hurricane
It hit me like a tidal wave
And I don't know why I drown my mind, it got the best of me
Answers
Answer:
uhm okay my dude
Answer:
cool poem
Step-by-step explanation:
will give brainliest

Answers
Answer:
B
Step-by-step explanation:
fill the blanks please
1-The ----------- of two events A and B is the event in which either A or B or both occur.
2- Calculate 5!--------- (no I am not shouting 5. "!" is reffering to factorial)
3- Two events are said to be:
------------ if they can not occur at the same time.
------------- if the occurance of one does not influence the probabilty of occurence for the other.
Answers
The blanks can be filled as: 1) union, 2) 120, 3) Mutually exclusive, Independent.
1- The union of two events A and B is the event in which either A or B or both occur.
The union of two events A and B includes all outcomes that belong to either A or B or both.
2- Calculate 5! (5 factorial) which is 5 x 4 x 3 x 2 x 1 = 120.
To calculate factorial of a positive integer n, multiply n by all positive integers less than n and greater than 0; alternatively, recursively multiply n by (n-1)!
3. Two events are said to be:
Mutually exclusive if they cannot occur at the same time.
Independent if the occurrence of one does not influence the probability of occurrence for the other..
Mutually exclusive events cannot occur together, while independent events can occur together but their occurrence does not affect each other.
To know more about union refer here:
https://brainly.com/question/23337676#
#SPJ11
can someone help me with this

Answers
The lengths of the line segments seen in the table are listed below:
DE = √10 BC = √40 AB = √181 FG = √346How to determine the lengths of line segments on Cartesian planeIn this problem we find six cases of line segments (\(\overline{AC}\), \(\overline{BC}\), \(\overline{DE}\), \(\overline{AB}\), \(\overline{EF}\), \(\overline{FG}\)), whose length have to be computed. Every length can be found by Pythagorean theorem:
l = √[(Δx)² + (Δy)²]
Where l is the length of the line segment between two ends.
Now we proceed to determine the length of each line segment:
Line segment AC
AC = √(8² + 3²)
AC = √73
Line segment BC
BC = √[(- 2)² + 6²]
BC = √40
Line segment DE
DE = √[(- 3)² + (- 1)²]
DE = √10
Line segment AB
AB = √[10² + (- 9)²]
AB = √181
Line segment EF
EF = √(5² + 3²)
EF = √34
Line segment FG
FG = √(11² + 15²)
FG = √346
To learn more on Pythagorean theorem: https://brainly.com/question/14930619
#SPJ1
