What is the half life for the zombie population
Answers
Answer:
.
Step-by-step explanation:
Related Questions
Which row of the table reveals the x-intercept of function f?

Answers
The row of the table that reveals the x-intercept of the function f is given as follows:
Second row.
What are the intercepts of a function?A function has two intercepts, which are listed as follows:
x-intercept.y-intercept.The definition of each type of intercept is given as follows:
x-intercept: values of x when y = 0.y-intercept: value of y when x = 0.From the second row of the table, we have that when x = -4, f(x) = 0, hence the x-intercept of the function is of x = -4.
The y-intercept is of y = -16, as from the fourth row, when x = 0, y assumes a value of 16.
More can be learned about the intercepts of a function at https://brainly.com/question/3951754
#SPJ1
can someone please answer this math question

Answers
Answer:
The answer is in the picture
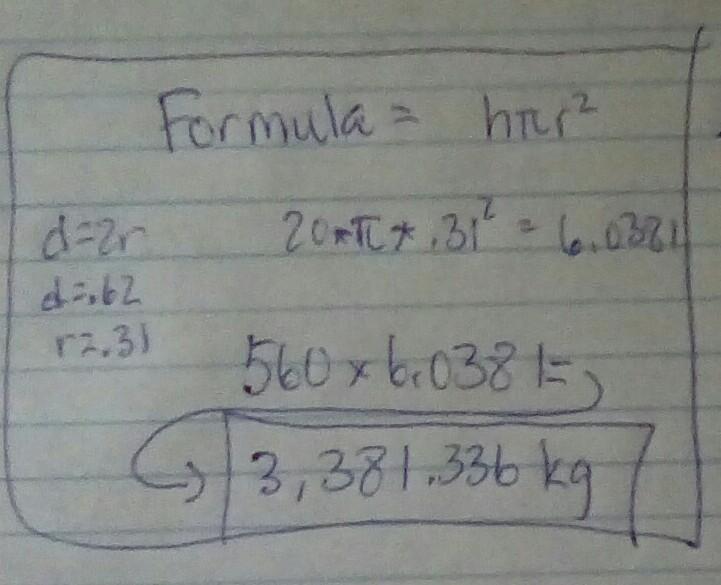
Someone plzzzzzz help me

Answers
Answer:
look below
Step-by-step explanation:
1. napping
2. Union
3. Let's meet at the park for a picnic
4. Put that down right now and don't look at it again
5. race
This might no be right I rushed
Answer:
1) Napping, Gray and Warm
2) Union(4), Uniform(3), Unicycle(2), Unicorn(1)
3)Let's meet at the park for a picnic.
4) Put that down right now and don't take it again!
5) Around
Step-by-step explanation:
Hope this Helps!!
:D
Find the value of x.
PLS help!!!! will give brainliest

Answers
Answer:
C.
Step-by-step explanation:
I can explain in comments if needed, but c is the correct answer :)
a system of equations is graphed on the coordinate plane. y=−6x−3y=−x 2 what is the solution to the system of equations? enter the coordinates of the solution in the boxes. (, )
Answers
The solution to the system of equations y = -6x - 3 and y = -x^2 can be found by finding the point(s) of intersection between the two graphs.
To solve the system, we can set the two equations equal to each other:
-6x - 3 = -x^2
Rearranging the equation, we get:
x^2 - 6x - 3 = 0
Using the quadratic formula, we can find the solutions for x:
x = (6 ± √(36 + 12))/2
x = (6 ± √48)/2
x = (6 ± 4√3)/2
x = 3 ± 2√3
Substituting these x-values back into either equation, we can find the corresponding y-values:
For x = 3 + 2√3, y = -6(3 + 2√3) - 3 = -18 - 12√3 - 3 = -21 - 12√3
For x = 3 - 2√3, y = -6(3 - 2√3) - 3 = -18 + 12√3 - 3 = -21 + 12√3
Therefore, the solutions to the system of equations are (3 + 2√3, -21 - 12√3) and (3 - 2√3, -21 + 12√3).
To know more about systems of equations click here: brainly.com/question/20067450
#SPJ11
Find the y-intercept of an equation whose slope is 2 and has the point (1, 5)
Answers
Answer:
The y-intercept is 3.
Step-by-step explanation:
I had to use a graph but if you mark the point on the graph. The slope is 2 so you would go up 2 right 1. But you can also do it the opposite way, go down 2 left 1. I hope this helps!
x4(-5) when x=-9 help please
Answers
Answer:
180
Step-by-step explanation:
-9*4=-36
-36*-5=180
The test scores for the students in Mr. Miller’s math class are shown here.
52, 61, 69, 76, 82, 84, 85, 90, 94
What is the range of the test scores?
Answers
The range of the test scores in Mr. Miller's math class is 42.
What is the range?Mathematically, the range refers to the difference between the highest value and the lowest value in a data set.
The range is computed by subtraction of the lowest value from the highest value.
Mr. Miller can use the range to measure the spread or dispersion of the test scores.
Test Scores:
52, 61, 69, 76, 82, 84, 85, 90, 94
Highest score = 94
Lowest score = 52
Range = 42 (94 - 52)
Thus, we can conclude that for the math students in Mr. Miller's class, the range of their test scores is 42.
Learn more about the range at https://brainly.com/question/24326172.
#SPJ1
Let's use the Intermediate Value Theorem (IVT) to prove the following theorems. (a) "Crossing-Graph Lemma": Prove that if f,g:[a,b]→R are continuous functions on [a,b] such that f(a)≤g(a) and f(b)≥g(b) (or vice versa), then there exists some c∈[a,b] such that f(c)=g(c). (b) "Fixed points on [0,1] ": Use part (a) to prove that if f:[0,1]→[0,1] is continuous, then f(c)=c for some c∈[0,1]. HINT: Which function g(x) will you use? Pay attention to the range of f !
Answers
(a) The Crossing-Graph Lemma states that if two continuous functions f and g are defined on an interval [a, b] and f(a) <= g(a) and f(b) >= g(b), then there exists some c in [a, b] such that f(c) = g(c).
(b) The Fixed-Points on [0, 1] Theorem states that if f is a continuous function from [0, 1] to [0, 1], then there exists some c in [0, 1] such that f(c) = c.
The lemma can be proved using the Intermediate Value Theorem. The IVT states that if a function f is continuous on an interval [a, b] and N is between f(a) and f(b), then there exists some c in (a, b) such that f(c) = N.
In the case of the Crossing-Graph Lemma, we can set N = g(a). Since f(a) <= g(a), the IVT guarantees that there exists some c in (a, b) such that f(c) = g(a).
But since g is also continuous, we know that g(c) = g(a). Therefore, we must have f(c) = g(c).
Here is a more detailed explanation of the Fixed-Points on [0, 1] Theorem:
We can use the Crossing-Graph Lemma to prove this theorem by setting g(x) = x. Since f(x) is continuous on [0, 1], we know that f(0) <= 0 and f(1) >= 1. Therefore, the Crossing-Graph Lemma guarantees that there exists some c in [0, 1] such that f(c) = g(c) = c.
Learn more about Graph here: brainly.com/question/17267403
#SPJ11
George has a triangle-shaped garden in his backyard. He drew a model of this garden on a coordinate grid with vertices A(4, 2), B(2, 4), and C(6, 4). He wants to create another, similar-shaped garden, A′B′C′, by dilating triangle ABC by a scale factor of 0.5. What are the coordinates of triangle A′B′C′?
A.
A′(2, 2), B′(1, 2), C′(3, 2)
B.
A′(2, 1), B′(1, 2), C′(3, 2)
C.
A′(8, 4), B′(4, 8), C′(12, 8)
D.
A′(2, 1), B′(1, 2), C′(6, 4)
Answers
Answer:
Hi! The correct answer is B: A' = (2, 1), B' = (1, 2), and C'=(3, 2).
Step-by-step explanation:
Why? because dilating a shape is basically multiplying it with the scale factor, so since the dilating factor is 1/2, you just divide all the numbers by 2.
4. Using the graph below, what is the solution to
-2x + 4 = -2? How can you tell?
4Y
2 4
Х
-2 O
2
-4

Answers
Answer:
(3, - 2 )
Step-by-step explanation:
The solution is at the point of intersection of the 2 lines
The lines intersect at (3, - 2 ) ← solution
Check by substituting x = 3 into the left side of the given equation
- 2(3) + 4 = - 6 + 4 = - 2 ← True
the span of a set of vectors is the set of all possible linear combinations of those vectors, and will always include the zero vector
Answers
The spam of the sets of vector of all linear combination is 0,
The span of the set {(2, 5, 3), (1, 1, 1)} is the subspace of R 3 consisting of all linear combinations of the vectors v 1 = (2, 5, 3) and,
v 2 = (1, 1, 1).
this defines a plane in R 3.
Since a normal vector to this plane in n = v 1 x v 2 = (2, 1, −3),
the equation of this plane has the form 2 x + y − 3 z = d for some constant d. the plane must contain the origin—it's a subspace— d must be 0.
A linear equation is an equation in which the highest power of the variable is always 1. it is also known as a one-degree equation. The standard form of a linear equation in one variable is of the form Ax + B = 0. Here, x is a variable, A is a coefficient and B is constant. There are three major forms of linear equations: point-slope form, standard form, and slope-intercept form. A linear equation only has one or two variables.No variable in a linear equation is raised to a power greater than 1 or used as the denominator of a fraction. When you find pairs of values that make a linear equation true and plot those pairs on a coordinate grid, all of the points lie on the same line
to know more about linear equation;
visit : brainly.com/question/28449784:
#spj4
Solve the system of equations below. 3x + 6y = 12
x + 2y = 4
A. (2, 1)
B. (0, 2)
C. No solution
D. Infinitely many solutions
Answers
Answer:
D
Step-by-step explanation:
When you put the equation into the calculator.... the results are infinitely many solutions.
Answer:
Step-by-step explanation:bans
Select the correct answer.
Simplify.
√96
A 24√4
B. 6√4
C 4√6
D. 16√6
Answers
Answer : C] 4√6
Thank you !
HELP ME PLEASEEE TY Abraham needs one-half of a point to get an A– in Math. What rational number can be used to represent the number of points needed for Abraham to get an A–?(1 point)
( ) point
Answers
The rational number that can be used to represent the number of points needed for Abraham to get an A will be 1.5.
What is a rational number?It should be noted that a rational number is the number that can be written as a fraction. It can be while numbers and decimals have well.
Therefore, since Abraham needs one-half of a point to get an A– in Math, the rational number that can be used to represent the number of points needed for Abraham to get an A willbe 1.5.
Learn more about rational numbers on:
brainly.com/question/12088221
#SPJ1
Consider the vector space C [0, 1] with inner product (f, g) = integral^1_0 f (x) g (x) dx. Determine whether the function f (x) = 3x is a unit vector in this space. If it is, then show that it is. If it is not, then find a function that is. (b) Find in exact form the cosine of the angle between f (x) = 5x^2 and g (x) = 9x.
Answers
The answer is A. The function g(x) = x is a unit vector in the vector space C[0, 1] and B. The cosine of the angle between \(f(x) = 5x^2\) and g(x) = 9x is 15 /\((2\sqrt{15})\).
To determine whether the function f(x) = 3x is a unit vector in the vector space C[0, 1] with the given inner product, we need to calculate its norm or magnitude.
The norm of a function f(x) in this vector space is defined as ||f|| = sqrt((f, f)), where (f, f) is the inner product of f with itself.
Using the inner product given, we can calculate the norm of f(x) as follows:
\(||f|| = sqrt(integral^1_0 (3x)^2 dx)\\= sqrt(integral^1_0 9x^2 dx)\\= sqrt[9 * (x^3/3) | from 0 to 1]\)
= sqrt[9/3 - 0]
= sqrt(3).
Since the norm of f(x) is sqrt(3) ≠ 1, we can conclude that f(x) = 3x is not a unit vector in this vector space.
To find a function that is a unit vector, we need to normalize f(x) by dividing it by its norm. Let's denote this normalized function as g(x):
g(x) = f(x) / ||f||
= (3x) / sqrt(3)
= sqrt(3)x / sqrt(3)
= x.
Therefore, the function g(x) = x is a unit vector in the vector space C[0, 1].
(b) To find the cosine of the angle between \(f(x) = 5x^2\) and g(x) = 9x, we can use the inner product and the definition of cosine:
cos(θ) = (f, g) / (||f|| ||g||).
Using the given inner product, we have:
\((f, g) = integral^1_0 (5x^2)(9x) \\\\dx= 45 * integral^1_0 x^3 \\\\dx= 45 * (x^4/4 | from 0 to 1)\)
= 45/4.
The norms of f(x) and g(x) are:
\(||f|| = sqrt(integral^1_0 (5x^2)^2 dx)\\= sqrt(integral^1_0 25x^4 dx)\\= sqrt[25 * (x^5/5) | from 0 to 1]\)
= sqrt(5).
\(= sqrt(integral^1_0 81x^2 dx)\)
\(= sqrt(integral^1_0 81x^2 dx)\)
\(= sqrt[81 * (x^3/3) | from 0 to 1]\)
\(= 3\sqrt{3}\)
Substituting these values into the cosine formula:
cos(θ) = (45/4) / (sqrt(5) * 3√3)
\(= (15/2) * (1 / (sqrt(5) * √3))= (15/2) * (1 / √15)= (15/2) * (1 / (√3 * √5))= 15 / (2√15).\)
Therefore, the cosine of the angle between \(f(x) = 5x^2 and g(x) = 9x is 15 / (2\sqrt{15}).\)
To learn more about vector space from the given link
https://brainly.com/question/11383
#SPJ4
Question 2
Use the technique of Laplace transformation to solve the differential equation
d^2y/dx +y=0 dx
for the initial conditions
dy(0)/dx = 2, y(0) = 1
Answers
To use the Laplace transformation to solve the following differential equation, we will first apply the transformation to the problem and its initial conditions. F(s) denotes the Laplace transform of a function f(x) and is defined as: \(Lf(x) = F(s) = [0,] f(x)e(-sx)dx\)
When the Laplace transformation is applied to the given differential equation, we get:
\(Ld2y/dx2/dx2 + Ly = 0\) .
If we take the Laplace transform of each term, we get: \(s^2Y(s) = 0 - sy(0) - y'(0) + Y(s)\).
Dividing both sides by \((s^2 + 1),\), we obtain:
\(Y(s) = (s + 2) / (s^2 + 1)\).
Now, we can use the partial fraction decomposition to express Y(s) in terms of simpler fractions:
Y(s) = (s + 2) / (\(s^{2}\)+ 1) = A/(s - i) + B/(s + i) .
Multiplying through by (\(s^{2}\) + 1), we have:
s + 2 = A(s + i) + B(s - i).
Expanding and collecting like terms, we get:
s + 2 = (A + B)s + (Ai - Bi).
Comparing the coefficients of s on both sides, we have:
1 = A + B and 2 = Ai - Bi.
From the first equation, we can solve for B in terms of A:B = 1 - A Substituting B into the second equation, we have:
2 = Ai - (1 - A)i
2 = Ai - i + Ai
2 = 2Ai - i
From this equation, we can see that A = 1/2 and B = 1/2. Substituting the values of A and B back into the partial fraction decomposition, we have:
Y(s) = (1/2)/(s - i) + (1/2)/(s + i). Now, we can take the inverse Laplace transform of Y(s) to obtain the solution y(x) in the time domain. The inverse Laplace transform of 1/(s - i) is \(e^(ix).\)
As a result, the following is the solution to the given differential equation:\((1/2)e^(ix) + (1/2)e^(-ix) = y(x).\)
Simplifying even further, we get: y(x) = sin(x)
As a result, given the initial conditions dy(0)/dx = 2 and y(0) = 1, the solution to the above differential equation is y(x) = cos(x).
For more such questions on Laplace transformation , visit:
https://brainly.com/question/29583725
#SPJ8
a house painter uses 0.7 gallons of paint for a wall that is 140 square feet. How much paint in gallons does she need to be able to cover 1900 square feet
Answers
Answer:
9.8 gallons
Step-by-step explanation:
1900÷140=13.5714285714
round up to 14
0.7x14=9.8
Directions: Read the problem. Then calculate the final price you would pay for the item, including tax
This is a Lamborghin[Veneno. The asking price for one of these is $4.5 million. It is the most expensive
production car in the world. The dealer will give you a 35% discount on the car. The tax rate is 7.75%.
What is the final price of the car, including tax? You may use a calculator, but you need to show your work
(what numbers and operations are you doing on your calculator?)
Final Price:
Answers
Answer:
Get to know the easy procedure on how to find 4500000 minus 35% is what along with steps by referring further.
As per the given data inputs P% = 35%, X= 4500000
We need to figure out the value of Y i.e. result obtained on subtracting 4500000 minus 35%
Substitute the given inputs in the formula i.e. Y= X(1-P%)
On substituting we get the data as under Y =4500000(1-35%)
Determine the value of 35% in decimal by simply dividing with 100 i.e. 35/100 =0.35
Replace the decimal value in terms of 35% in the equation.
Thus, we get the equation as Y = 4500000(1-0.35)
On simplifying it further by performing basic maths operations we get Y =4500000(0.65)
Finally, we get the value of Y as 2925000
Therefore 4500000 minus 35% is 2925000
plus 7.75%
total answer: 3151687.5
Step-by-step explanation:
I NEED HELP ASAPPP
Solve x
X-1/2=1/10
Answers
Answer:
3/5 (Already there but I wanted to put an explanation)
Step-by-step explanation:
first you want to change the 1/2 to work better with the 1/10. The way you can do is change the 1/2 to be 5/10 by multiplying both sides of the fraction by 5 so that it is out of 10 rather than out of 2. you then add 5/10 to 1/10 to get x=6/10. since 6/10 can be simplified by 2, you divide both sides of the fraction by 2 to get 3/5=x
What are the coordinates of the midpoint A(5, 8) and B(-1, -4)
Answers
Answer:
(2, 2)Step-by-step explanation:
Given points
A(5, 8) and B(-1, -4)Midpoint formula
x = (x1+x2)/2 = (5 - 1)/2 = 2y = (y1 + y2)/2 = (8 - 4)/2 = 2Midpoint is (2, 2)
15. Federico necesita resolver el problema de encontrar la medida x, en centímetros, del lado del cuadrado de
la figura.
Sabe que el área total de la figura es 45 centímetros cuadrados y determina que el problema se puede
resolver utilizando la ecuación
8x
2
= 45
Las soluciones correctas de esta ecuación son x = -9 y x = 5. Para resolver el problema inicial, de las dos
soluciones de la ecuación, Federico debe presentar como respuesta
A. -9, porque nueve es el único cuadrado perfecto en las soluciones.
B.
C.
las dos, porque al ser soluciones de la ecuación lo son del problema.
ninguna, porque la ecuación no corresponde al problema.
D. 5, porque el lado del cuadrado debe ser un valor positivo.
Answers
Al encontrar la medida x del lado del cuadrado, Federico debe presentar como solución igual a 5, ya que el lado del cuadrado debe ser un valor positivo.
¿Cómo calcular el área del cuadrado?Como el cuadrado es una figura geométrica que tiene lados iguales, para realizar el cálculo, debemos tomar la medida de uno de los lados y elevarlo al cuadrado. El cálculo se puede realizar mediante la siguiente fórmula:
A = L²Por lo tanto, la geometría plana se usa para calcular las medidas precisas de la habitación en relación con su área, longitud y altura.
La respuesta correcta es la opción D.
Encuentre más sobre geometría aquí:
https://brainly.com/question/19241268
#SPJ1
Find the equation of the line that passes through points A and B

Answers
Answer:
y= 2x-1
Step-by-step explanation:
We know two points on the line, so we can find the slope
(2,3) and (4,7)
The slope is found by using the slope formula
m = ( y2-y1)/(x2-x1)
m = ( 7-3)/(4-2) = 4/2 = 2
We can use the slope intercept form of the equation
y = mx+b where m is the slope and b is the y intercept
y = 2x+b
Using one of the points to substitute into the equation we can find b
3 = 2(2)+b
3 = 4+b
-1 =b
y= 2x-1
Answer:
y = 2x - 1
Step-by-step explanation:
The equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
Calculate m using the slope formula
m = \(\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\)
with (x₁, y₁ ) = A (4, 7 ) and (x₂, y₂ ) = B (2, 3 )
m = \(\frac{3-7}{2-4}\) = \(\frac{-4}{-2}\) = 2 , then
y = 2x + c ← is the partial equation
To find c substitute either of the 2 points into the partial equation
Using (2, 3 )
3 = 4 + c ⇒ c = 3 - 4 = - 1
y = 2x - 1 ← equation of line
Determine how many terms of the following convergent series must be summed to be sure that the remainder is less than 10−2
[infinity]∑k=1(−1)k+1k4
Answers
There are 16 terms of the convergent series must be summed to be sure that the remainder is less than 10⁻²[infinity]∑k=1(−1)k+1k4
The alternating series estimation theorem can be used to determine an upper bound for the error in approximating the total of the series by summing a finite number of terms. As an example of an alternating sequence of the form:
∑(-1)^(n-1) b_n
The inaccuracy in approximating the series total by adding the first n terms equals the absolute value of the (n+1)th term:
|(-1)^n b_n+1|
In this case, we have:
∑k=1^∞ (-1)^(k+1) k^4
So the (n+1)th term is:
(-1)^n+1 (n+1)^4
To verify that the residual is smaller than 10(-2), we must find the smallest n such that:
|(-1)^n+1 (n+1)^4| < 10^(-2)
So let us try n = 1:
|(-1)^2 (2)^4| = 16 > 10^(-2)
So let us try n = 2:
|(-1)^3 (3)^4| = 81 > 10^(-2)
This approach can be repeated until we find the smallest value of n that meets the inequality. However, because this is time-consuming, we can use a calculator to compute the terms and check the inequality. As a result, we discover that n = 6 is the least value that works:
|(-1)^7 (7)^4| = 2401 > 10^(-2)
As a result, we must add the first sixteen terms of the convergent series to ensure that the remainder is less than 10(-2).
To learn more about convergent visit:
https://brainly.com/question/15415793
#SPJ11
find the slope of (-3,1) and (2,-9)
Answers
Answer:
The slope would be -2
Step-by-step explanation:
-9-1/2+3= -2
5. 3x = 6. 40x how many time do I need to multiply thee number for them to be the ame
Answers
The equation 3x = 6.4 can be solved for x by dividing both sides of the equation by 3: 3x/3 = 6.4/3; x = 2.13
So, for 3x and 6.4x to be equal, x must be equal to 2.13. This means that you need to multiply the number 6.4 by 2.13 to equal 3. The equation 3x = 6.4 represents the relationship between two variables, x and 3x. We are trying to find the value of x that would make 3x equal to 6.4. To do this, we divide both sides of the equation by 3. Dividing both sides of an equation by the same number does not change the relationship between the variables; it only scales down the variable's value by the same factor.
So, by dividing both sides of the equation by 3, we get:
3x/3 = 6.4/3
x = 2.13
Finally, to make 6.4x equal to 3, we need to divide 6.4 by 2.13: 6.4 / 2.13 = 3. So, we need to multiply 6.4 by 2.13 to equal 3.
To learn more about equation, visit here
https://brainly.com/question/29657983
#SPJ4
Painting a wall goes slowly, so you divide your team into two smaller teams.
Team A paints 7 walls in 2 hours.
Team B paints 4 walls in 1 hour.
Who worked faster?
Answers
Convert from Celsius to Fahrenheit.

Answers
Answer:
212°F is the answer using the formula
Answer:
212 F
Step-by-step explanation:
You can use the below formula to convert °C to F.
\(\frac{9}{5}C+32=F \)
So now , according to the question you have to convert 100°C in to F.
For that you have to put 100 instead of C to the given formula.
Let us solve now.
\(\frac{9}{5}C+32=F \)
\(\frac{9}{5}*100+32=F \)
\(\frac{900}{5} +32=F\)
\(180+32=F\)
\(212=F\)
Therefore,
212 F = 100°C
Hope this helps you :-)
Let me know if you hve any other questions :-)
Allison earns $8.50 an hour at her job serving at iHop, and also earns $9 each hour she tutors her little brother in math. She graphs the amount of hours
she works at her iHop job (x) and the number of hours she tutors (y) to determine how to eam at least $870. Which type of boundary line should she use in
her graph?
Answers
Answer:
i
Step-by-step explanation:
you can buy 7 oranges for 8.50 what is the price per orange
Answers
Answer:
The price of one orande is 1.21.
Step-by-step explanation:
Answer:
Short Version: 1.21
Long Version: 1.21428571
Step-by-step explanation:
Just divide 8.50 by 7