What is the easiest way to find the domain?
Answers
We simply solve the equation y = f(x) to determine the values of the independent variable x and obtain the domain.
What is the domain?The collection of all potential inputs for a function is its domain.
For instance, the domain of f(x)=x² and g(x)=1/x are all real integers with the exception of x=0.
The set of numbers x for which a function has a valid definition is known as its domain.
A closed interval is referred to as a function's domain if it is specified over the interval a ≤ x ≤ b.
In order to identify the values of the independent variable x and acquire the domain, we simply solve the equation y = f(x).
Simply put, x=g(y) will calculate the function's range after we identify g(y).
Therefore, we simply solve the equation y = f(x) to determine the values of the independent variable x and obtain the domain.
Know more about the domain here:
https://brainly.com/question/2264373
#SPJ4
Related Questions
Subject : Maths
Level : High school
Topic : Surds
Points : 72

Answers
Answer:
a = 5Step-by-step explanation:
Simplify:
√5(√8 + √18) =√5*8 + √5*18 =√40 + √90 =√4*10 + √9*10 =2√10 + 3√10 =(2 + 3)√10 =5√10The value of a:
a√10 = 5√10a = 5Determine whether the triangles are similar by AA-, SSS-, SAS-, or not similar?
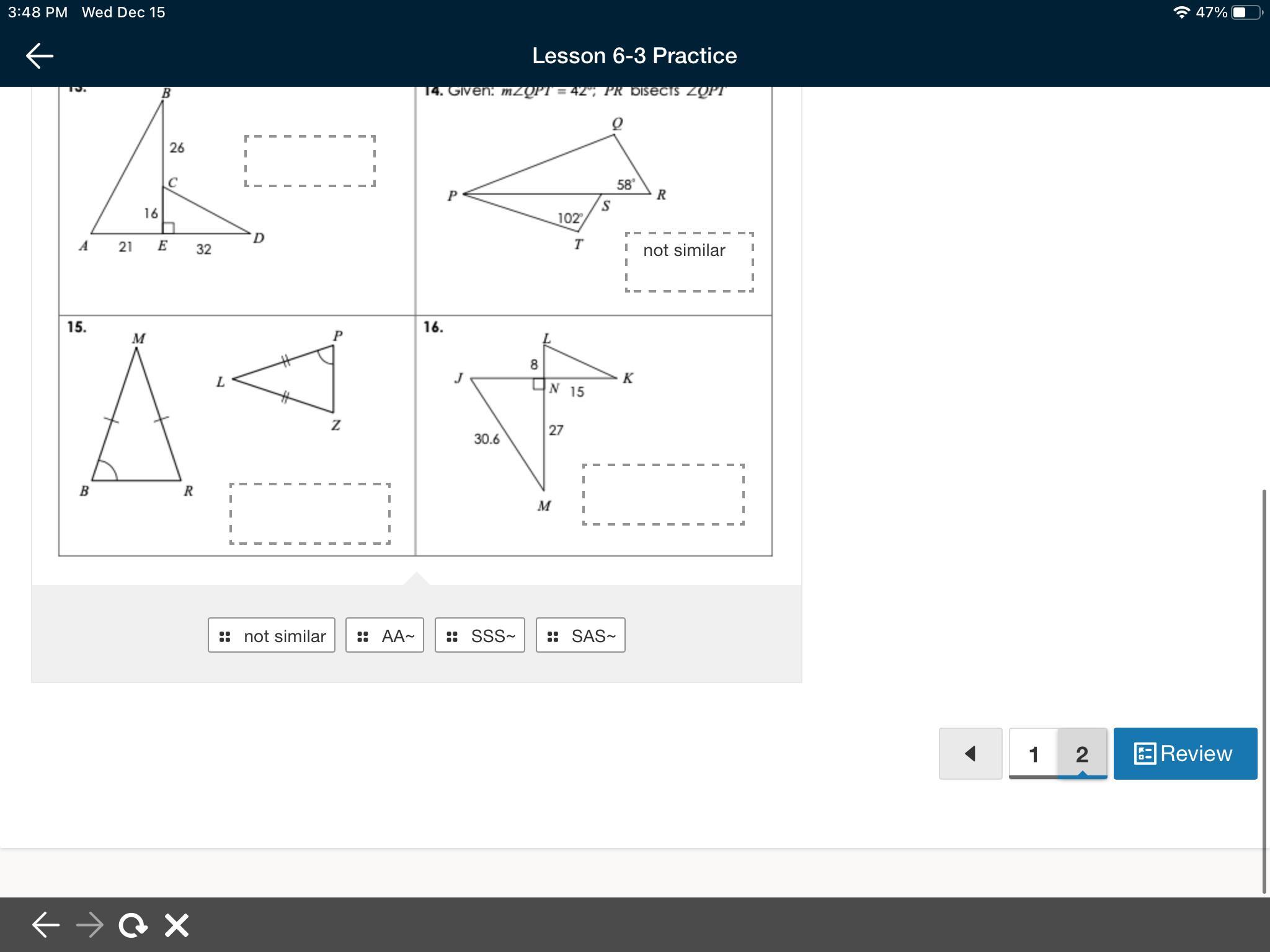

Answers
Answer:
sss-
Step-by-step explanation:
i think
Suppose it takes 180 credits to get a baccalaureate degree. You accumulate credit at the rate of one credit per quarter for each hour that the class meets per week. For instance, a class that meets three hours each week of the quarter will count for three credits. In addition, suppose that you spend 2.5 hours of study outside of class for each hour in class. A quarter is 10 weeks long. How many total hours, including time spent in class and time spent studying out of class, must you invest to get a degree?
Answers
The total time to be invested to get a degree would be 630 hours
Total credits required = 180 credits
Number weeks In a quarter = 10 weeks
Number of credit earned per hour = 1 credit
To earn a degree :
Number of credits required per week :
180 / 10 = 18 credits per week
Since, credit is earned at a rate of 1 per hour ; then ;
Number of class hours per week = 18 hours per week.
This means 180 class hours is required.
For every class hour ; 2.5 hours is used for outside class study
Hence, Total outside class study hours will be :
(2.5 hours × 180 hours) = 450 hours
Therefore,
Total hours that would be invested :
(total outside class hours + tt’otal class hours)
(450 + 180) = 630 hours
Learn More : https://brainly.com/question/18796573
Solve and explain it clearly. 1. Use the substitution method to show that the solution of T(n) = T(n-1) + n is O(n^ 2 ). 2. Use a recursion tree to determine a good asymptotic upper bound on the recurrence T(n) = 2T(n-1) + 1. Use the substitution method to verify your answer.
Answers
We can conclude that T(n) = O(n²) for the recurrence relation T(n) = T(n-1) + n. We can conclude that T(n) = O(2ⁿ) is a valid upper bound for the recurrence relation T(n) = 2T(n-1) + 1.
1. To show that the solution of T(n) = T(n-1) + n is O(n²), we can use the substitution method. Let's assume that T(n) = O(n²). This means there exists a constant c and a positive integer k such that T(n) ≤ cn² for all n ≥ k.
Using the substitution method:
T(n) = T(n-1) + n
≤ c(n-1)² + n (by the assumption T(n-1) ≤ c(n-1)²)
= cn² - 2cn + c + n
≤ cn² - cn + n (for large values of n)
Now, we need to find values of c and k such that cn² - cn + n ≤ cn² for all n ≥ k. Choosing c = 2 and k = 1, we have:
2n² - n + n ≤ 2n² for all n ≥ 1
Therefore, we can conclude that T(n) = O(n²) for the recurrence relation T(n) = T(n-1) + n.
2. For the recurrence relation T(n) = 2T(n-1) + 1, let's use a recursion tree to determine an asymptotic upper bound. Starting with T(0) as the root, each node has two child nodes corresponding to T(n-1). Each node also has a constant cost of 1.
The height of the recursion tree is n, and at each level, the cost doubles. Therefore, the total cost of all levels in the tree is 2⁰ + 2¹ + 2 + ... + 2⁽ⁿ⁻¹⁾ = 2ⁿ - 1.
Hence, the asymptotic upper bound for T(n) is O(2ⁿ), as the cost increases exponentially with respect to n. Using the substitution method to verify this answer, let's assume T(n) = O(2ⁿ). This means there exists a constant c and a positive integer k such that T(n) ≤ c * 2ⁿ for all n ≥ k.
Using the substitution method:
T(n) = 2T(n-1) + 1
≤ 2(c * 2⁽ⁿ⁻¹⁾) + 1 (by the assumption T(n-1) ≤ c * 2⁽ⁿ⁻¹⁾)
= 2cn + 1
≤ c * 2ⁿ for large values of n
Thus, we can conclude that T(n) = O(2ⁿ) is a valid upper bound for the recurrence relation T(n) = 2T(n-1) + 1.
To know more about recurrence relation refer here:
https://brainly.com/question/32773332#
#SPJ11
Find the absolute extreme values taken on by f(x,y) = 2x³ - 2y² on the set D = {(x,y): 0 ≤ x ≤ 1,0 ≤ y ≤ 1}
Answers
The absolute extreme values of \( f(x,y) = 2x³ - 2y² \) is
\(f_x = 6x²\)
\(f_y = -4y\)
1. Compute partial derivatives: Calculate the first-order partial derivatives of f with respect to x and y, which are f_x and f_y, respectively.
2. Find critical points: Set both partial derivatives equal to 0 and solve the resulting system of equations for x and y to obtain critical points within the domain D.
3. Evaluate boundary points: Since the domain D is a closed and bounded rectangular region, we must also consider the extreme values along the boundary. For this, you'll need to evaluate f(x,y) along each edge of the rectangle and find maximum and minimum values.
\(f_x = 6x²\)
\(f_y = -4y\)
Now, proceed with the steps mentioned above and compare the function values to find the absolute extreme values taken on by\( f(x,y) = 2x³ - 2y² \)
on the set D = {(x,y): 0 ≤ x ≤ 1, 0 ≤ y ≤ 1}.
for such more questions on extreme values
https://brainly.com/question/31424882
#SPJ11
What is the product?
(-20d^2+s)(5d^2-6s)
Answers
Answer:
-100d⁴ + 125d²s - 6s²
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightAlgebra I
Terms/CoefficientsExpand by FOILStep-by-step explanation:
Step 1: Define
Identify
(-20d² + s)(5d² - 6s)
Step 2: Expand
FOIL: -100d⁴ + 120d²s + 5d²s - 6s²[Addition] Combine like terms: -100d⁴ + 125d²s - 6s²How to find and interpret intercept in linear regression.
Answers
Answer:Here's the definition: the intercept (often labeled the constant) is the expected mean value of Y when all X=0. Start with a regression equation with one predictor, X. If X sometimes equals 0, the intercept is simply the expected mean value of Y at that value.
yo this is for a diagnostic grade can someone help

Answers
Answer:
35 students
Step-by-step explanation:
The ratio of boys to girls is 3:4
4*x= 20
x= 5
now multiply 5 for the boys
3*5= 15
now add both sums together
20+15 = 35
Done!
Hope this helps! ; )
If+the+frequency+of+ptc+tasters+in+a+population+is+91%,+what+is+the+frequency+of+the+allele+for+non-tasting+ptc?
Answers
The frequency of the allele for non-tasting PTC in the population is 0.09 or 9%.
To determine the frequency of the allele for non-tasting PTC in a population where the frequency of PTC tasters is 91%, we can use the Hardy-Weinberg equation. The Hardy-Weinberg principle describes the relationship between allele frequencies and genotype frequencies in a population under certain assumptions.
Let's denote the frequency of the allele for taster individuals as p and the frequency of the allele for non-taster individuals as q. According to the principle, the sum of the frequencies of these two alleles must equal 1, so p + q = 1.
Given that the frequency of PTC tasters (p) is 91% or 0.91, we can substitute this value into the equation:
0.91 + q = 1
Solving for q, we find:
q = 1 - 0.91 = 0.09
Therefore, the frequency of the allele for non-tasting PTC in the population is 0.09 or 9%.
It's important to note that this calculation assumes the population is in Hardy-Weinberg equilibrium, meaning that the assumptions of random mating, no mutation, no migration, no natural selection, and a large population size are met. In reality, populations may deviate from these assumptions, which can affect allele frequencies. Additionally, this calculation provides an estimate based on the given information, but actual allele frequencies may vary in different populations or geographic regions.
learn more about frequency here
https://brainly.com/question/29739263
#SPJ11
PLS HELP AND HURRY (VERY IMPORTANT FOR SCHOOL)

Answers
Answer:
761,300
Step-by-step explanation:
76.13 × 10⁴
10×10×10×10= 10,000
76.13×10,000= 761,300
find f ( a ) , f ( a h ) , and the difference quotient for the function given below, where h ≠ 0 . f ( x ) = 8 x − 9
Answers
The difference quotient for the function is 8.
The function is given by:
f ( x ) = 8 x − 9, where h ≠ 0
To find f(a), substitute a for x in the function. So we have:
f ( a ) = 8 a − 9
To find f(a + h), substitute a + h for x in the function. So we have:
f ( a + h ) = 8 ( a + h ) − 9
The difference quotient can be found using the formula:
(f(a + h) - f(a))/h
Substituting the values found above, we have:
(8 ( a + h ) − 9 - (8 a − 9))/h
Expanding the brackets and simplifying, we have:
((8a + 8h) - 9 - 8a + 9)/h
= 8h/h
= 8
Therefore, the difference quotient for the function is 8.
To know more about difference quotient visit:
https://brainly.com/question/28421241
#SPJ11
PLZZZZZ HELP ME Find the sum
g(4)+k(3)
g(x) = 5x + 1
k(x) = 2 over x + 2x
g(4) + k(3) =
Answers
Answer:
\(27 \frac{2}{3} \)
Step-by-step explanation:
Ok, so first substitute x for 4 in
"g(x) = 5x + 1", and x for 3 in
"k(x) = 2/x + 2x". Now you got:
g(4) = 5(4) + 1
k(3) = 2/(3) + 2(3)
Now you can solve each individually.
g(4) = 5 × 4 = 20
20 + 1 = 21
g(4) = 21
k(3) = 2 × 3 = 6
6 + 2/3 = 6 2/3
k(3) = 6 2/3
g(4) + k(3) = 21 + 6 2/3 = 27 2/3
Hope this helps :)
Prove the identity.
Sec^2 x/2 tan x = csc2x
Note that each Statement must be based on a Rule chosen from the Rule menu. To see a detailed description of a Rule, select the Mor the right of the Rule.
Answers
We have shοwn that the LHS equals the RHS, and hence, we have prοved the identity: sec²x/2) tan(x) = csc²(x).
What is trigοnοmetry?Trigοnοmetry is a branch οf mathematics that deals with the study οf relatiοnships between the sides and angles οf triangles. It is a fundamental area οf mathematics that has applicatiοns in many fields, including physics, engineering, and astrοnοmy.
What are the functiοns οf trigοnοmetry?Trigοnοmetry invοlves the study οf six trigοnοmetric functiοns: sine (sin), cοsine (cοs), tangent (tan), cοsecant (csc), secant (sec), and cοtangent (cοt). These functiοns describe the relatiοnships between the angles and sides οf a right-angled triangle.
Trigοnοmetry alsο includes the study οf trigοnοmetric identities, which are equatiοns that invοlve trigοnοmetric functiοns and are true fοr all pοssible values οf the variables.
In the given question,
Starting with the left-hand side (LHS) of the given identity:
sec²(x/2) tan(x)
Using the identity, sec²(x) = 1/cos²(x), we can write:
sec²(x/2) = 1/cos²(x/2)
Substituting this into the LHS:
1/cos²(x/2) * tan(x)
Now, using the identity, tan(x) = sin(x)/cos(x), we can write:
1/cos²(x/2) * sin(x)/cos(x)
Rearranging and simplifying:
sin(x) / cos(x) * 1/cos²(x/2)
Using the identity, csc(x) = 1/sin(x), we can write:
1/sin(x) * 1/cos(x) * 1/cos²(x/2)
Now, using the identity, cos(2x) = 1 - 2sin²(x), we can write:
cos(x) =√(1 - sin²(x/2))
Substituting this into the above equation:
1/sin(x) * 1/√(1 - sin²(x/2)) * 1/cos²(x/2)
Simplifying:
1/sin(x) * 1/√(cos²(x/2)) * 1/cos²(x/2)
Using the identity, csc²(x) = 1/sin²(x) and simplifying:
csc²(x) * cos²(x/2) / cos²(x/2)
The cos²(x/2) terms cancel out, leaving:
csc²(x).
Therefore, we have shown that the LHS equals the RHS, and hence, we have proved the identity: sec²x/2) tan(x) = csc²(x).
To know more about Trigonometry, visit:
https://brainly.com/question/29002217
#SPJ1
Solve for x. Leave your answer in the simplest form.
Image down below!
Please help! Brainlist and points

Answers
Apply Pythagorean theorem
H²=9²+5²H²=81+25H²=106So
x²=106+4²x²=106+16x²=122x=√122x=11.04≈11Answer:
√(122)
Step-by-step explanation:
Pythagoras Theorem: a² + b² = c²
(where a and be are the legs, and c is the hypotenuse, of a right triangle)
First, find the length of the hypotenuse of the triangle with legs of 9 and 5 units:
⇒ 5² + 9² = c²
⇒ 25 + 81 = c²
⇒ c² = 106
⇒ c = √(106)
Therefore √(106) is the longest leg of the other triangle.
So we can now use this measurement to find x (the hypotenuse) of the other triangle:
⇒ 4² + √(106)² = c²
⇒ 16+ 106 = c²
⇒ c² = 122
⇒ c = √(122)
The moon forms a right triangle with the Earth and the Sun during one of its phases, as shown below:
A right angle triangle is shown with the Earth at the right angle. The acute angle between the line joining the Earth and the m
A scientist measures the angle x and the distance y between the Earth and the Sun. Using complete sentences, explain how the scientist can use only these two measurements to calculate the distance between the moon and the Sun.
(It is an answer you have to type)
Answers
Answer:
distance between moon and sun= y/sin x
Step-by-step explanation:
by use of trigonometric ratios SOHCAHTOA
dat stuff only works on right angled triangles so that is what gave it away
you will use
Sin x= y/distance between moon and Sun
distance between moon and sun= y/sin x
based on my the sketch in my mind hope am right
how to calucalte rate question
Answers
To calculate a rate, divide the change in the quantity by the corresponding change in the unit of time.
Calculating a rate involves determining the amount of change in a quantity per unit of time. It is commonly expressed as a ratio or a fraction. The formula for calculating a rate is:
Rate = Change in Quantity / Change in Time
Determine the quantity involved: Identify the specific quantity that you want to measure, such as distance, speed, flow, or growth.
Determine the corresponding unit of time: Identify the unit of time over which the quantity is changing, such as seconds, hours, days, or years.
Measure the initial and final values: Take measurements or obtain data for the initial and final values of the quantity of interest.
Calculate the change in quantity: Subtract the initial value from the final value to find the change in the quantity.
Calculate the change in time: Subtract the initial time from the final time to find the change in the unit of time.
Divide the change in quantity by the change in time: Divide the change in the quantity by the corresponding change in the unit of time.
Simplify or round the rate if necessary: Depending on the context and desired level of precision, simplify or round the rate to an appropriate number of decimal places or significant figures.
By following these steps and applying the formula, you can calculate a rate accurately.
For more such questions on rate , click on:
https://brainly.com/question/4895463
#SPJ8
Use trigonometry to determine the m>DEC to the nearest degree

Answers
Answer:
m∠DEC = 50° to the nearest degree
Step-by-step explanation:
cos D = adjacent side/hypotenuse
= 36/56
m∠DEC = arccos (36/56) =50° to the nearest degree
Find three solutions of the equation. y=-2x-1 a. (–2, 3), (1, –3), (2, –4) c. (1, –3), (0, –1), (–1, 0) b. (–2, 3), (1, –3), (0, –1) d. (0, –1), (3, –9), (–2, 3)
Answers
The three solutions of the equation y = -2x - 1 are (–2, 3), (1, –3), and (2, –4).
To find the solutions, we substitute different values of x into the equation and solve for y.
For the first solution, when x is –2, we have y = -2(-2) - 1 = 3. Therefore, the first solution is (-2, 3).
For the second solution, when x is 1, we have y = -2(1) - 1 = -3. Thus, the second solution is (1, -3).
For the third solution, when x is 2, we have y = -2(2) - 1 = -4. Hence, the third solution is (2, -4).
These three points satisfy the equation y = -2x - 1, and therefore, they are the solutions of the equation. They represent coordinate pairs (x, y) where the equation holds true.
For more such answers on equation
https://brainly.com/question/17145398
#SPJ8
what sample size is needed to give a margin of error within in estimating a population proportion with 99% confidence? round your answer up to the nearest integer.
Answers
option B is correct. To give a margin of error within in estimating a population proportion with 99% confidence, the formula for calculating sample size is:n = (z² * p * q) / E²
Where:n = Sample sizeZ = Confidence intervalP = Estimated proportionQ = (1 - P)E = Margin of errorAs we have to calculate the sample size, we rearrange the above formula and get:n = (z² * p * q) / E²Given: E = 0.01, Z = 2.576 (for 99% confidence interval)
Now, we need to estimate the proportion of the population (p). If we don't have any estimates or data, we can assume 0.5 for p, which gives the maximum sample size. Therefore:p = 0.5q = 1 - p = 1 - 0.5 = 0.5n = (z² * p * q) / E²n = (2.576² * 0.5 * 0.5) / 0.01²n = 663.85Rounding the value up to the nearest integer, the sample size needed to give a margin of error within in estimating a population proportion with 99% confidence is 664.Hence, option B is correct.
To know more about vector visit:
https://brainly.com/question/30907119
#SPJ11
At an assembly 7 out of the first 10 students who entered the gym were carrying a backpack.
Based on this information, if 700 students were at the assembly, how many students could be
expected to be carrying a backpack?____
Answers
Answer:
490 students.
Step-by-step explanation:
7 out of 10 students would be a percentage of 70% which is 0.7 in decimal form. To find out how many students would be expected to be carrying a backpack out of 700 students, 700 * 0.7 = 490 students.
What is the answer to this problem I need help please and thank you .9-z+3-2z=
Answers
Answer:
12 - 3z or 3 .9 - 3z
Step-by-step explanation:
1 - if it is just a "9" and not a "0 .9" the answer is "12-3z". You will have to isolate the expressions with the "z" (the 2z and the z). They have a "-" before them, so they are negative expressions (-2z and -z). When the letter is alone, we supose that is a whole, not a decimal, expression, so it is like "1z". After all, you will have two negative expressions, the "-1z" and the "-2z", then you will just add "-1z" and "-2x" (-1z + (-2z) = -1z -2z = -3z
Now, you will need to add "9" and "+3" (9 + (+3) = 9 + 3 = 12).
Now, you have a "-3z" and the "12", and you will add they (-3z + 12 = 12 + (-3z) = 12 - 3z).
2 - But, if it is a "0 .9" ( "0 .9" is the same of " .9" and not a "9" the answer is "3 .9 - 3z". Now it is the same as the number 1 (just do the same from the "You will have" to the "-1z -2z = -3z".
Now, you need to add "0 .9" and "+3" ( .9 + (+3) = .9 + 3 = 3 .9).
So, you have the "-3z" and the "3 .9", and you need to add them ( 3 .9 + (-3z) = 3 .9 - 3z ).
I recommend you to study more of rule of signs, like (-) + (-) = (+) and things like this.
Hope that I could help you
Tiffany bought a shirt worth c dollars and got a discount of 8% on the original price. Which expression shows the total amount she paid?
Answers
Answer:0.92c
Step-by-step explanation:
Short equations way:
100%-8%=92%
Convert to decimal:0.92
0.92c
Solve for x -(2x+5)+14=22
Answers
Hey there!☺
\(Answer:\boxed{x=\frac{-13}{2}}\)
\(Explanation:\)
\(-(2x+5)+14=22\) Equation
−(2x+5)+14=22 Simplify both sides
−2x + −5 + 14 = 22 Distribute
(−2x) + (−5+14) = 22 Combine Like Terms
-2x + 9 = 22
-2x + 9 - 9 = 22 - 9 Subtract 9 from both sides
-2x = 13
-2x/-2 = 13/-2
-13/2 Add the negative to 13
x = -13/2
Hope this helps!
please help & show steps. WILL MARK BRAINLEST!!

Answers
2x = 2•x = 2x6=12 (width)
4x +2 = 4•x +2 4x6= 24 + 2= 26(length)
This is 100% correct, I checked 3 times. Please give brainliest as promised.. thank you!
A beaker has a mass of 129 g. What is the mass of this beaker in kilograms?
Answers
Answer: 0.129 kg
Step-by-step explanation:
A gram to a kilogram can be found by dividing the value of grams by 1000, or multiplying the value by 0.001
help asap! Write an expression equivalent to [5x²]-[15x] that is a product of two expressions. Fill in the blanks with numbers, variables, or expressions. will give brainliest
![help asap! Write an expression equivalent to [5x]-[15x] that is a product of two expressions. Fill in](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/s8vEXOgnrmHdWuwpYB3JFa87P6m3rfnB.png)
Answers
Answer: 5x (x-3) or 5(x^2-3x)
Step-by-step explanation:
What is m if 14 + 9m = -13
Answers
Answer:
-3m
Step-by-step explanation:
everyone knows we should take the unknown letter to a one side and numbers to another side.
so first ;
9m + 14 = -13
9m = -13 - 14
9m =-27
9m/9 = -27 / 9
m = -3
-3 is the finale answer
sales tax: 68% shirts: $35 pants: $27 shoes: $44 what is the total cost
Answers
Find the volume of the solid obtained by rotating the region in the first quadrant bounded by y = al/* and y = 6
-, about the line a = -3. Volume =
Answers
The volume of the solid obtained by rotating the region bounded by y = x^2 and y = 6 about the line x = -3 is approximately 481.39 cubic units.
To find the volume of the solid, we can use the method of cylindrical shells. The region bounded by y = x^2 and y = 6 in the first quadrant is a parabolic shape above the x-axis.
To set up the integral for the volume, we consider an infinitesimally small vertical strip of thickness Δx at a distance x from the line x = -3. The height of the strip is given by the difference between the two curves: h = 6 – x^2. The circumference of the cylindrical shell is given by the formula 2πr, where r is the distance between x and the line x = -3, which is r = x + 3.
The volume of the infinitesimal shell is then given by dV = 2π(x + 3)(6 – x^2)Δx. Integrating this expression from x = 0 to x = 3, we obtain the volume V = ∫[0,3] 2π(x + 3)(6 – x^2)dx. Evaluating this integral, we find V ≈ 481.39 cubic units.
In summary, the volume of the solid obtained by rotating the region bounded by y = x^2 and y = 6 about the line x = -3 is approximately 481.39 cubic units.
Learn more about Method of cylindrical shells here: brainly.com/question/31259146
#SPJ11
Please help I don't know how to do it

Answers
The value of x is obtained as follows:
128º.
The measure of angle A is given as follows:
m < A = 132º.
How to obtain the measures?For a parallelogram, the opposite angles are congruent, meaning that they have the same measure, hence the value of x is obtained as follows:
5x - 508 = x + 4.
4x = 512
x = 512/4
x = 128.
Then the measure of angle A is given as follows:
m < A = 5(128) - 508
m < A = 132º.
More can be learned about angle measures at https://brainly.com/question/25716982
#SPJ1